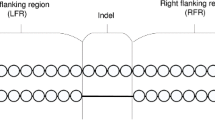
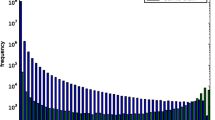
The publication of the crystallographic structure of calmodulin protein has offered an example leading us to believe that it is possible for many protein sequence segments to exhibit multiple 3D structures referred to as multi-structural segments. To this end, this paper presents statistical analysis of uniqueness of the 3D-structure of all possible protein sequence segments stored in the Protein Data Bank (PDB, Jan. of 2003, release 103) that occur at least twice and whose lengths are greater than 10 amino acids (AAs). We refined the set of segments by choosing only those that are not parts of longer segments, which resulted in 9297 segments called a sponge set. By adding 8197 signature segments, which occur uniquely in the PDB, into the sponge set we have generated a benchmark set. Statistical analysis of the sponge set demonstrates that rotating, missing and disarranging operations described in the text, result in the segments becoming multi-structural. It turns out that missing segments do not exhibit a change of shape in the 3D-structure of a multi-structural segment. We use the root mean square distance for unit vector sequence (URMSD) as an improved measure to describe the characteristics of hinge rotations, missing, and disarranging segments. We estimated the rate of occurrence for rotating and disarranging segments in the sponge set and divided it by the number of sequences in the benchmark set which is found to be less than 0.85%. Since two of the structure changing operations concern negligible number of segment and the third one is found not to have impact on the structure, we conclude that the 3D-structure of proteins is conserved statistically for more than 98% of the segments. At the same time, the remaining 2% of the sequences may pose problems for the sequence alignment based structure prediction methods.












Similar content being viewed by others
Abbreviations
- amino acid:
-
AA
- Protein Data Bank:
-
PDB
- root mean square distance:
-
RMSD
- root mean square distance for unit vector sequence:
-
URMSD
- three-dimensional:
-
3D
References
Anfinsen, C. B. (1973). Science 81:223–233
Barrientos L. G., Louis J. M., Botos I., Mori T., Han Z., O’Keefe B. R., Boyd M. R., Wlodawer A., Gronenborn A. M. (2002). Structure 10(5):673–686
Bamborough P., Duncan D., Richards W. G. (1994) Protein Eng. 7(9):1077–1082
Berman H. M., Westbrook J., Feng Z., Gilliland G., Bhat T. N., Weissig H., Shindyalov I. N., Bourne P. E. (2000) Nucleic Acids Res. 28:235–242
Brody S. S., Gough S. P., Kannangara C. G. (1999) Proteins 37(3):485–493
Chen K., Ruan J., and Kurgan, L. A. (2006) The Protein J. 25:(1), 57–70
Chew L. P., Huttenlocher D., Kedem K., Kleinberg J. (1999) J. Comput. Biol. 6(3–4):313–325
Ding J., Das K., Hsiou Y., Sarafianos S. G., Clark A. D., Jacobo-Molina A., Tantillo C., Hughes S. H., Arnold E. (1998) J. Mol. Biol. 284(4):1095–1111
Drum C. L., Yan S.-Z., Bard J., Shen Y.-Q., Lu D., Soelaiman S., Grabarek Z., Bohm A., Tang W. J. (2002) Nature 415:396–402
Elshorst B., Hennig M., Forsterling H., Diener A., Maurer M., Schulte P., Schwalbe H., Griesinger C., Krebs J., Schmid H., Vorherr T., Carafoli E. (1999) Biochemistry 38(38):12320–12332
Falzone C. J., Wang Y., Vu B. C., Scott N. L., Bhattacharya S., Lecomte J. T. (2001) Biochemistry 40: 4879–4891
Hansson M., Gough S. P., Brody S. S. (1997) Proteins 27(4):517–522
Kabsch W. (1978) Acta Crystallogr. A34:827–828
Kihara D., Skolnick J. (2003) J. Mol. Biol. 334:793–802
Korolev S., Hsieh J., Gauss G. H., Lohman T. M., Waksman G. (1997) Cell 90(4):635–647
Lindberg J., Sigurdsson S., Lowgren S., Andersson H. O., Sahlberg C., Noreen R., Fridborg K., Zhang H., Unge T. (2002) Eur. J. Biochem. 269(6):1670–1677
Meador W. E., Means A. R., Quiocho F. A. (1992) Science 257(5074):1251–1255
Reva B. A., Finkelstein A. V., Skolnick J. (1998) Fold Des. 3(2):141–147
Schumacher M. A., Crum M., Miller M. C. (2004) Structure (Camb) 12(5):849–860
Shen, S. Y., Yu, T., Kai, B., Ruan, J. S. (2004). J. Eng. Math. 21:(6), 862–870 (in Chinese)
Tiraboschi G., Jullian N., Thery V., Antonczak S., Fournie-Zaluski M. C., Roques B. P. (1999) Protein Eng. 12(2):141–149
Toyoshima C., Nakasako M., Nomura H., Ogawa H. (2000) Nature 405(6787): 647–655
Toyoshima C., Nomura H. (2002) Nature 418(6898):605–611
Veerapandian B. (1992) Biophys. J. 62(1):112–115
Xu C., Rice W. J., He W., Stokes D. L. (2002) J. Mol. Biol. 316(1):201–211
Yap K. L., Yuan T., Mal T. K., Vogel H. J., Ikura M. (2003) J. Mol. Biol. 328(1):193–204
Yona G., Kedem K, (2005) J. Comput. Biol. 12(1):12–32
Author information
Authors and Affiliations
Corresponding author
Additional information
*Jishou Ruan research was supported by Liuhui Center for Applied Mathematics, China-Canada exchange program administered by MITACS and NSFC (10271061).
#Ke Chen and Lukasz A. Kurgan research was partially supported by NSERC Canada.
†Jack A. Tuszynkski research has been supported by MITACS, NSERC Canada and the Allard Foundation.
Appendix 1
Appendix 1
For proving that an absolutely conserved segment must be a conserved segment, we first consider the definition of URMSD. We need to prove the following statement mathematically.
Let
be the URMSD between the two unit vector sequences \(\left\{{v_i}\right\}_{i=1}^n\) and \(\left\{{w_i}\right\}_{i=1}^n\), and let d i be the URMSD between the pair of \(v_{i+1},\ldots,v_{i+5}\) and \(\phi (w_{i+1}),\ldots,\phi (w_{i+5})\).
Then \(d(\{v_i\},\{w_i\})\leq \max\{d_i\;\vert \;i=0,1,2,\ldots,n-5\}\) for all \(n\geq 10\).
Proof. It is easily followed that
We can regard that \(\sum\limits_{i=1}^n (v_i,\phi (w_i))\) as the trace of the correlation matrix R(n), where
That is, we have
For a fixed ϕ and every pair of five-unit-vector \(v_{i+1}, \ldots ,v_{i+5}\) and \(\phi (w_{i+1}),\ldots ,\phi (w_{i+5})\), we have a correlation matrix
Let \(d_i =\sqrt{\hbox{trace}(R_i (5)^\prime R_i (5))}\) for \(i=0,1,2,\ldots ,n-5\). For convenience, then we may assume \(d_0 =\max\{d_i\;\vert \;i=0,1,2,\ldots ,n-5\}\), then
Considering the relationship
By ordinary fact of structure of protein: for most AAs, the state at site i is not more frequently correlated to the state at site j if the distance between the two sites is greater than 5 AAs. That is, we may assume that \(R(n)^\prime R(n)\) has the following relations mathematically:
-
The number of the set \(\left\{{k\;\vert \;\sum\limits_{j=1}^5 \sum\limits_{i=1}^5 {(v_i,\phi (w_j))^2 <\sum\limits_{j=1}^5 \sum\limits_{i=1}^5 {(v_{i+k},\phi (w_j))^2}}} \right\}\) related to n − 5 is very small.
-
The number of the set \(\left\{{k\;\vert \;\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_i,\phi (w_j))^2 <\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_i,\phi (w_{j+k}))^2}}} \right\}\) is also very small related to n − 5.
-
\((v_i,\phi (w_j))^2>(v_{i+k},\phi (w_j))^2\) and \((v_i,\phi (w_j))^2>(v_i,\phi (w_{j+k}))^2\) for all \(i,j\leq 5\) and almost all k > 6.
Then let \(y_i =\phi (w_i)\), we have
-
\(\sum\limits_{j=1}^5 \sum\limits_{i=1}^5 {(v_i,y_j)^2 \geq\sum\limits_{j=5}^5 \sum\limits_{i=1}^5 {(v_{i+k},y_j)^2}}\),
-
\(\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_i,y_j)^2 \geq\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_i,y_{j+k})^2}}\)
-
\(\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_i,y_j)^2 \geq\sum\limits_{i=1}^5 \sum\limits_{j=1}^5 {(v_{i+k},y_{j+k})^2}}\)
for all k > 6. Without lost the generality, we may assume that \(n=0\;(\hbox{mod}5)\), and then we have
That is, we have proved that
where \(\sigma_i (j)\) for \(j=5,n\) and \(i\leq j\), are the singular value of R(5) and R(n) respectively. Replacing R(n) and R(5) by their “squared root”:
and with the same argument, we have
That is, \(\frac{\hbox{trace}(svd\;R(5))}{5}>\frac{\hbox{trace}(svd\;R(n))}{n}\) for \(n\geq 10\).
Therefore, the maximal URMD among the all five-unit-vectors is greater than the URMSD for the whole segment. This ends the proof.
Rights and permissions
About this article
Cite this article
Ruan, J., Chen, K., Tuszynski, J.A. et al. Quantitative Analysis of the Conservation of the Tertiary Structure of Protein Segments. Protein J 25, 301–315 (2006). https://doi.org/10.1007/s10930-006-9016-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10930-006-9016-5