Introduction

Recent papers by [1] and [2] show the application of fractional calculus to pharmacokinetics (PK). The paper of [1], shows the use of a single parameter Mittag–Leffler function [3]:

$$ E_{\alpha } \left( z \right) = \sum\limits_{i = 0}^{\infty } {{\frac{{z^{i} }}{{\Upgamma \left( {\alpha i + 1} \right)}}}} $$
(1)

in place of the mono-exponential:

$$ e^{z} = \sum\limits_{i = 0}^{\infty } {{\frac{{z^{i} }}{i!}}} = \sum\limits_{i = 0}^{\infty } {{\frac{{z^{i} }}{{\Upgamma \left( {i + 1} \right)}}}} = E_{1} \left( z \right) $$
(2)

If drug is given as a bolus dose in a venous site, drug concentration in plasma at a time t after the dose administration, C(t), can be represented using a response function of the form:

$$ C(t) = Dose \, \left[ {\theta E_{\alpha } \left( { - \lambda t^{\alpha } } \right)} \right] $$
(3)

where Dose is the amount of drug given, λ and θ1 have the interpretation of the elimination rate constant and the reciprocal of volume of distribution of the plasma compartment, respectively, if model (3) is seen as solution corresponding to a single compartment model described by a (Caputo) fractional differential equation of order α [4], see, e.g., [5, 6].

The paper of [2] shows solutions for some specific two- and three-compartmental structures described by fractional order kinetics. However, as pointed out by [7], while the connection between response function and compartmental structure is immediate for the single compartment case, this is less so for the case of multi-compartmental ones.

The purpose of this communication is to discuss this connection, and to do so we will (1) clarify the distinction between different types of systems of fractional differential equations, in particular discussing the difference between commensurable and non-commensurable ones, (2) show solutions for the corresponding response functions, and (3) discuss their application to the modeling of PK data.

Commensurate fractional order linear systems

Commensurate fractional order linear systems are described by a system of linear fractional differential equations (FDE) of the form [8]:

$$ {\frac{{D_{\blacktriangle }^{{^{\alpha } }} }}{{{\text{d}}t}}}{\mathbf{x}}(t) = \left( {\begin{array}{*{20}c} {{\frac{{D_{\blacktriangle }^{{^{\alpha } }} }}{{{\text{d}}t}}}x_{1} (t)} \\ \ldots \\ {{\frac{{D_{\blacktriangle }^{{^{\alpha } }} }}{{{\text{d}}t}}}x_{m} (t)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {a_{11} } & \ldots & {a_{1m} } \\ \ldots & \ldots & \ldots \\ {a_{m1} } & \ldots & {a_{mm} } \\ \end{array} } \right){\mathbf{x}}(t) + {\mathbf{f}}(t) = A{\mathbf{x}}(t) + {\mathbf{f}}(t) $$
(4)

with initial conditions\( {\mathbf{x}}(0) = {\mathbf{x}}_{0} \), where \( D_{\blacktriangle }^{{^{\alpha } }} \) is the Caputo fractional differential operator [4] of order α > 0, and \( {\mathbf{f}}(t) \)is the (vector valued) input function to the system. These systems are called commensurate because all the differential equations are of the same fractional order, α. As a consequence t can be shown that the solution to the system of FDE [4] represents the entire state of the system at any given time. In particular, a compartmental system can be obtained, for 0 < α ≤ 1, exactly as for a system of ODE, by introducing mass-balance constrains:

$$ a_{ji} \ge 0,\quad i \ne j $$
(5)

and the following:

$$\begin{array}{*{20}c} {\text{a}}_{ii} \le 0 \\ \left| {{\text{a}}_{ii} } \right|\ge \sum\limits_{\begin{array}{l} j = 1 \\ j \ne i\end{array} }^{m} {a_{ji} } \hfill \\ \end{array} $$
(6)

which guarantee that all states are non-negative. It can be shown (see e.g. [8]) that the solutions to the system of linear FDE (4) depend on the eigenvalues of its characteristic equation, that is, in the Laplace domain, \( \det \left( {B(s) = A(s) - sI} \right) \). In particular if the eigenvalues are real and distinct the solution to Eq. 4 takes the formFootnote 1:

$$ {\mathbf{X}}(t) = b_{1} {\mathbf{u}}_{1}^{(1)} E_{\alpha } (\lambda_{1} t^{\alpha } ) + b_{2} {\mathbf{u}}_{2}^{(2)} E_{\alpha } (\lambda_{1} t^{\alpha } ) + \cdots + b_{m} {\mathbf{u}}_{m}^{(m)} E_{\alpha } (\lambda_{1} t^{\alpha } ) $$
(7)

where b 1, b 2, …, b m are constants, λ1, λ2, …, λ m and \( {\mathbf{u}}_{1}^{(1)} ,{\mathbf{u}}_{2}^{(2)} , \ldots ,{\mathbf{u}}_{m}^{(m)} \) are the eigenvalues and eigenvectors of the characteristic equation for (4). It is immediate from (7) that for a bolus input in the j-th compartment the solution for drug concentration in the same compartment takes the form:

$$ C_{j} (t) = Dose\left[ {\theta_{1} E_{\alpha } (\lambda_{1} t^{\alpha } ) + \theta_{2} E_{\alpha } (\lambda_{2} t^{\alpha } ) + \cdots + \theta_{m} E_{\alpha } (\lambda_{m} t^{\alpha } )} \right] $$
(8)

which establishes a direct connection with the familiar multi-exponential response function corresponding to ordinary multi-compartment linear systems with distinct eigenvalues.

Non-commensurate fractional order linear systems

A non-commensurate fractional order linear system is described by [8]:

$$ \left( {\begin{array}{*{20}c} {{\frac{{D_{\blacktriangle }^{{^{{\alpha_{1} }} }} }}{{{\text{d}}t}}}x_{1} (t)} \\ \ldots \\ {{\frac{{D_{\blacktriangle }^{{^{{\alpha_{m} }} }} }}{{{\text{d}}t}}}x_{m} (t)} \\ \end{array} } \right) = A{\mathbf{x}}(t) + {\mathbf{f}}(t) $$
(9)

where now α 1, α 2, …, α m are distinct (real positive) numbers indicating the fractional order for each equation. As remarked by [7], in reference to the systems of compartments shown in (2), the equations in [9] do not satisfy mass-balance even if conditions (5) are satisfied, and in general the solution to the system of FDE (9) does not represent the states of the system. Non-negativity is also no longer guaranteed by the relationships (6) (and there are non-trivial issues associated with demonstrating the stability, observability and reach-ability of such systems, see [9].)

Numerical methods must be employed to find the solution to (9), since a close form solution equivalent to (7) does not exist [10, 11]. However, solutions can be obtained if is assumed that the fractional orders are rational numbers, that is α i  = p i /q i where p i , q i are integers, i = 1, …, m (12).Footnote 2 The mathematics necessary to obtain the general solution are quite involved, and for the purpose of this paper we only show a subset of the possible solutions, in particular for C(t) (see [11–13] for more general results). For a non-commensurate system, it can be shown that a solution for drug concentration in the j-th compartment takes the form:

$$ C_{j} (t) = Dose\left\{ {t^{{\gamma - \alpha_{j} }} \left[ {\theta_{1} E_{{\gamma ,\gamma - \alpha_{j} + 1}} (\lambda_{1} t^{\gamma } ) + \theta_{2} E_{{\gamma ,\gamma - \alpha_{j} + 1}} (\lambda_{2} t^{\gamma } ) + \cdots + \theta_{m} E_{{\gamma ,\gamma - \alpha_{j} + 1}} (\lambda_{m} t^{\gamma } )} \right]} \right\} $$
(10)

where γ = 1/q, q = M.C.D(q 1, …, q m ), and \( E_{\alpha ,\beta } \left( z \right) = \sum\limits_{i = 0}^{\infty } {{\frac{{z^{i} }}{{\Upgamma \left( {\alpha i + \beta } \right)}}}} \) is the two-parameters Mittag–Leffler function (5). One notices two important facts: first, this solution only depends on the fractional order for compartment j, α j , and γ, second in direct analogy to the solution (8) above, the Mittag–Leffler function exponents are determined by the eigenvalues of the characteristic equation for the system.

Example

We now have the ingredients to show a simple example of applications of multi-terms Mittag–Leffler response functions to fit PK data. We consider the case m = 2, which for a standard ODE system generates the response function:

$$ C(t) = Dose\left( {\theta_{1} e^{{\lambda_{1} t}} + \theta_{2} e^{{\lambda_{2} t}} } \right) $$
(11)

for a commensurate FDE system obtains:

$$ C(t) = Dose\left( {\theta_{1} E_{\alpha } (\lambda_{1} t^{\alpha } ) + \theta_{2} E_{\alpha } (\lambda_{2} t^{\alpha } )} \right) $$
(12)

and for a non-commensurate FDE system

$$ C(t) = Dose \, t^{\gamma - \alpha } \left( {\theta_{1} E_{\gamma ,\gamma - \alpha + 1} (\lambda_{1} t^{\gamma } ) + \theta_{2} E_{\gamma ,\gamma - \alpha + 1} (\lambda_{2} t^{\gamma } )} \right) $$
(13)

The parameters θ1, θ2, λ1, λ2, α, γ are estimated from the data, with the constraints θ1, θ2 > 0, λ1, λ2 < 0, and 0 < γ, α ≤ 1, which guarantee that Eq. 13 is non-negative and non-increasing (strictly monotone) for t ≥ 0.Footnote 3 To evaluate the single and two-parameters Mittag–Leffler function we implemented a FORTRAN 90 version the algorithm reported in [14]. We used the computer program NONMEM [15] to obtain the parameters estimates.

As a check, Fig. 1 shows the Mittag–Leffler function for the same choice of parameters used in Fig. 11 of [16], α = 1 and 0 < β ≤ 2. Contrary to α, which has a strong influence on the overall shape of the curve, the parameter β has its most pronounced influence on the value of the function at t = 0.

Fig. 1
figure 1

The Mittag–Leffler function E α,β(−t) for α = 1 and β ∈ (0, 2)

Full size image

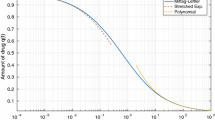
Figure 2 shows the fit of models (11) (solid line), (12) (widely dashed line), and (13) (dashed line), to error corrupted data simulated using an eight compartments mammillary model. Note the added flexibility introduced by use of a sum of single- and two-parameters Mittag–Leffler functions in respect to exponentials: the values of minus twice log-likelihood for the fit of the simulated data were −316.895, −381.974, and −406.354, for models (11)–(13), respectively. Of course, this is just an example to show the feasibility of the approach: for this simulation, a sum of exponentials would fit the simulated data perfectly well.

Fig. 2
figure 2

Simulated data (circles) with superimposed the fit of the response function for a second order ordinary system, Eq. 11 in the text (solid line), commensurate FDE, Eq. 12 (widely dashed line), and non-commensurate FDE, Eq. 13 (dashed line)

Full size image

Final remarks

Following up on the papers of [1] and [2], and the commentary by [7], the first purpose of this commentary is to further clarify the nature of systems of FDE, and in particular to point out the distinction between commensurate and non-commensurate ones. Commensurate systems of FDE have a direct relationship with system of ODE, and in particular when formulated in terms of compartmental models (that is, satisfying mass balance and non-negativity constraints, see Eqs. 5, 6 they can be used to characterize the states of PK systems. Non-commensurate systems of FDE do not, in general, represent the state of a system.

Leaving to the side the issue of what exactly system (9) represents, one is still justified in using it as a black-box type model for single-input/single-output experiments, as long as physical constraints (non-negativity in particular) are satisfied. To do so response functions are a convenient tool, and we show that, for commensurate and non-commensurate FDE, relatively simple ones can be derived which satisfy such requirements. The solutions for a system of commensurate FDE takes the form of the sum of Mittag–Leffler functions, with a single parameter α, Eq. 8, while solutions for a system of non-commensurate FDE can be expressed by a sum of two-parameters Mittag–Leffler functions, such as Eq. 10. As a consequence, one can establish a direct analogy between the familiar sum of exponentials used in PK, and importantly all the relationships between compartmental transfer rate constants and the intercepts and exponents of the corresponding response functions found in classic textbooks on PK [17, 18], carry forward to fractional differential equations.

In conclusion, while insight into the physiological interpretability of FDE system might be gained in the future, and the formulation of non-commensurate systems of FDE to represent the states of a system (required by, e.g., a physiological flow model) requires further investigation, the response functions (8) and (10) can be used to investigate the existence of PK data sets which might actually show complex fractional kinetics.Footnote 4