1 Introduction

Fiber reinforced plastic composites (FRP) have many advantages such as high specific strength, specific stiffness, etc. [1,2,3,4]. However, these materials suffer from different damage mechanisms, such as matrix cracking, fiber breakage and delamination [5,6,7,8]. The principal mode of failure in laminated composites is the separation along the interfaces of the layers, viz, delamination [9,10,11,12,13,14]. This failure results in dramatic reduction of residual strength and stiffness of the structure. Delamination occurs under different loading conditions, i.e. mode I, mode II and mode III. However, mode I delamination is the most common mode of failure occurred in the structures. This is due to lower energy that is required for the initiation of mode I delamination [15,16,17].

Due to complexity of laminated composites, prediction of fatigue behavior in these materials is not straight forward [18]. Accurate measurement of fatigue crack growth has become a challenging issue in fracture mechanics analyses. Fatigue crack growth monitoring is a difficult and time-consuming test [19]. In addition, work gets harder when the crack is embedded within the structure and could not be seen visually.

Acoustic emission (AE) is a naturally occurring phenomenon, which is the result of transient elastic wave propagation caused by a sudden release of energy inside the material [20]. There are various sources of AE events in composite materials such as matrix cracking, fiber/matrix debonding, fiber breakage, etc. [21,22,23]. Recently, AE has been utilized as an applicable technique to detect in-situ information from the damages that occur in laminated composites [5, 24,25,26,27].

Some studies have used AE technique to investigate the delamination behavior under quasi-static loading condition [28,29,30,31,32]. Fotouhi and Ahmadi [33] investigate initiation of delamination in laminated composites under mixed-mode loading condition using AE technique. Arumugam et al. [34] investigated damage mechanisms in glass/epoxy composite specimens under mode I delamination using AE and fast Fourier transform (FFT) analysis. Saeedifar et al. [35] determined interlaminar fracture toughness of glass/ epoxy composites under mode I, II and mixed-mode I&II loading using AE and finite element (FE) methods. The literature review shows that most AE based studies were focused on delamination initiation and there is a lack in the investigation of delamination propagation behavior using AE technique.

Due to the complexity of the fatigue phenomenon in composite materials, little work has been done on the behavior of delamination in laminated composites under cyclic loading using AE technique. Silversides et al. [36] studied delamination initiation in carbon/epoxy specimens under mixed-mode cyclic loading conditions. Romhany et al. [37] offered an algorithm to predict delamination crack in carbon/epoxy specimens subjected to cyclic loading. Romhany’s method has two disadvantages: (a) to predict the fatigue crack growth at least two AE sensors must be utilized, and (b) the accurate AE wave propagation speeds in the specimens must first be calculated.

The aim of this paper is to investigate the delamination propagation in glass/epoxy composites under mode I quasi-static and fatigue loading conditions. The article is composed of two sections. In the first section, the delamination behavior under quasi-static loading condition is investigated using the mechanical and AE data. Then, the correlations between AE energy, the released strain energy and the crack growth are established theoretically and it is found that there is a 3rd degree polynomial correlation between the crack growth and the cumulative AE energy. Then, quasi-static delamination growth was predicted using the obtained correlation and the obtained AE signals. In the second section, the delamination crack growth under fatigue loading is predicted using the same concept as the static loading. The advantage of the proposed method is prediction of delamination crack growth using only one AE sensor without any need to determine AE wave propagation speed in the specimens. Consistency of the AE-based evaluated results and visually recorded values illustrates that the proposed AE method is more suitable than the conventional methods for detection of delamination crack growth in the laminated composites under quasi-static and fatigue loading conditions.

2 Experimental Procedures

2.1 Materials and Specimens’ Preparation

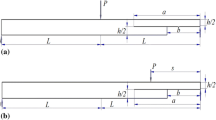
The experimental work was carried out on laminates fabricated from an epoxy resin reinforced with unidirectional and woven E-glass fibers with the density of 1.17 \(\hbox {g/cm}^{3}\), 390 and 300 \(\hbox {g/m}^{2}\), respectively. The laminates were prepared by hand lay-up method. The starter crack was formed by inserting a Teflon film with a thickness of 20 \(\upmu \)m at the mid-plane during molding as an initial crack for the delamination. The laminated composite specimens consist of ten plies with a rectangular shape and uniform thickness. Characteristics of the specimens used for this study are illustrated in Fig. 1. For ease of use, the unidirectional specimen is called U and the woven specimen is called W.

Fig. 1
figure 1

The specimens geometry and dimensions

Full size image

2.2 Test Procedure

2.2.1 Quasi-Static and Cyclic Loadings

The specimens were subjected to quasi-static loading according to ASTM D5528 standard [38]. A properly calibrated tensile test machine (HIWA), in the range of 0.5–500 mm/min, and the displacement control mode were used for the tests. The tests were carried out at room temperature and at a constant displacement rate of 3 mm/min. The load and displacement were continuously recorded by the tensile machine and the crack length was recorded using a digital video camera (SONY HDR-XR150) with 25X optical zoom and 300X digital zoom.

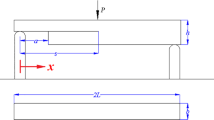
The fatigue loading tests were performed by a properly calibrated tensile test machine (Dartec) according to ASTM D6115 [39]. Based on ASTM D6115 recommendation the tests were performed under displacement control mode with the loading frequency of 3 Hz. For ease of working, the quasi-static and fatigue tested specimens are illustrated by ‘S’ and ‘F’ subscripts, respectively. The test apparatus is shown in Fig. 2.

Fig. 2
figure 2

The experimental test setup

Full size image

2.2.2 AE Device

AE events were recorded using AE software AEWin and a data acquisition system Physical Acoustics Corporation (PAC) PCI-2 with a maximum sampling rate of 40 MHz. PICO which is a broadband, resonant-type, single-crystal piezoelectric transducer from PAC, was used as the AE sensor. The sensor has the resonance frequency of 513.28 kHz and an optimum operating range of 100–750 kHz. In order to provide good acoustic coupling between the specimen and the sensor, the surface of the sensor was covered with grease. The signal was detected by the sensor and enhanced by a 2/4/6-AST preamplifier. The gain selector of the preamplifier was set to 37 dB. The test sampling rate was 1 MHz with 16 bits of resolution between 10 and 100 dB. The AE sensor was placed on the surface of the sample with 80 mm distance from the delamination tip.

Fig. 3
figure 3

Load-displacement and crack growth-displacement diagrams for the \(\hbox {U}_{\mathrm{S1}}\) and \(\hbox {W}_{\mathrm{S1}}\) specimens

Full size image
Fig. 4
figure 4

Fiber bridging and crack plane changing in the investigated specimens a \(\hbox {U}_{\mathrm{S1}}\), and b \(\hbox {W}_{\mathrm{S1}}\)

Full size image
Fig. 5
figure 5

Fiber bundle and pure resin tensile tests

Full size image
Fig. 6
figure 6

Frequency distribution of matrix and fiber damages

Full size image
Fig. 7
figure 7

Load- displacement and Frequency distribution of AE signals of the \(\hbox {U}_{\mathrm{S1}}\) specimen

Full size image
Fig. 8
figure 8

Load-displacement and cumulative AE energy of delamination curves for the \(\hbox {U}_{\mathrm{S1}}\) and \(\hbox {W}_{\mathrm{S1}}\) specimens

Full size image

3 Results and Discussion

3.1 Quasi-Static Loading

3.1.1 Mechanical Results

Figure 3 shows the load-displacement and crack growth-displacement diagrams for the \(\hbox {U}_{\mathrm{S1}}\) and \(\hbox {W}_{\mathrm{S1}}\) specimens. As can be seen, the crack growth in the \(\hbox {W}_{\mathrm{S1}}\) specimen is more stable than the \(\hbox {U}_{\mathrm{S1}}\) specimen. These instabilities i.e. rise and fall behaviors, in the crack growth and load-displacement diagrams are called pop-in phenomenon [40]. The big pop-ins in the \(\hbox {U}_{\mathrm{S1}}\) specimen occur due to fiber bridging phenomenon [38, 41, 42]. Fiber bridging phenomenon described as the stretching of some fibers between upper and lower layers of the crack plane. This phenomenon occurs near the crack tip and results in additional resistance against the crack growth [41, 42]. When the stress in the bridged fibers reaches to the fibers strength, the fibers are broken and the crack propagates abruptly for a few millimeters. By bridging the new fibers, the crack is arrested again. Some small pop-ins in the \(\hbox {W}_{\mathrm{S1}}\) specimen are due to the change in delamination propagation plane that is a common phenomenon in non-unidirectional laminated composites (see Fig. 4). The top images of Fig. 4 show the macroscopic lateral view of the specimens. In the case of the \(\hbox {U}_{\mathrm{S1}}\) specimen, bridged fibers between upper and lower surfaces of the crack are obvious, while in the case of the \(\hbox {W}_{\mathrm{S1}}\) specimen, no bridged fiber is seen. However, in the lateral view of the \(\hbox {W}_{\mathrm{S1}}\) specimen, changing of the crack growth plane is observed. This is due to this fact that when the crack propagates and arrives to a warp of the woven fabric, it may not be able to continue its growth at the previous plane and it jumps from the warp and propagates at the adjacent layers. The bottom images of Fig. 4 show the microscopic view of the damaged surface of the specimens. In consistent with the macroscopic images, fiber bridging is observed in the \(\hbox {U}_{\mathrm{S1}}\) specimen surface, while complete breaking of a layer and changing the crack growth plane are seen for the \(\hbox {W}_{\mathrm{S1}}\) specimen.

Fig. 9
figure 9

Changing the strain energy due to infinitesimal crack growth under displacement control mode (a and da are crack length and infinitesimal crack growth, respectively)

Full size image
Table 1 The values of released strain energy (dU) and AE energy jump \((\mathrm{dE}_{\mathrm{AE}})\) at each pop-in for the \(\hbox {U}_{\mathrm{S1}}\) specimen
Full size table

3.1.2 AE Results

The most common damage mechanisms in laminated composites are matrix cracking, fiber breakage, and delamination [43,44,45]. In order to estimate delamination growth using AE technique, first, the AE signals originated from delamination damage must be specified and discriminated from the AE signals originated from other damage mechanisms. To this aim, tensile tests on pure resin and fiber bundle were conducted. The pure resin tensile test was performed on a tensile test sample made of epoxy resin and the fiber bundle test was conducted by a tension test on a bundle of about 1000 glass filaments. The AE signals were recorded by the AE sensors that were mounted on the surface of the resin and the fiber bundle (see Fig. 5). The AE signals obtained from the fiber bundle and pure resin tests were analyzed using Fast Fourier Transform (FFT) and the frequency range of the matrix damage and fiber breakage were obtained (see Fig. 6). As can be seen, frequency range of the matrix and fiber damages are (70–170 kHz) and (350–500 kHz), respectively.

The AE signals captured during the DCB tests can be classified according to the obtained frequency ranges for the pure resin and fiber bundle. Fig. 7 shows the load-displacement and the frequency distribution of the recoded AE signals for the U\(_{S1 }\)specimen. According to the frequency content of the AE signals, three distinct classes are observed. In consistency with the obtained frequency ranges of pure resin and fiber bundle tests (Fig. 6), class 1 signals are allocated to matrix cracking and class 3 signals are dedicated to fiber breakage. The only remained class with frequency range of [170–230 kHz] (i.e. class 2) is devoted to the only remained damage mechanisms, i.e. delamination. The frequency range of delamination is in consistent with the results of the previous research [46].

The following results, i.e. figures, tables, etc., are only related to the AE signals originated from delamination damage that are discriminated from the other damage mechanisms. Figure 8 shows load and cumulative AE energy of delamination versus displacement curves for the \(\hbox {U}_{\mathrm{S1}}\) and \(\hbox {W}_{\mathrm{S1}}\) specimens. In consistency with the crack growth curve in Fig. 3, each pop-in in the load curve is related to a sudden crack growth which is accompanied by a well-defined acoustic energy jump. By applying the load to the specimen, as long as the crack is arrested, the strain energy is stored in the specimen. When the stored strain energy reaches to its critical value, the crack propagates and the stored strain energy is released (see Fig. 9). According to Fig. 9, released strain energy at each pop-in (\({\hbox {dU}} \big |_{\Delta } )\), can be calculated by Eq. (1) [47]:

$$\begin{aligned} {\hbox {dU}} \big |_{\Delta } =\frac{{1}}{{2}}{\Delta }\cdot \hbox {dP} \end{aligned}$$
(1)

\(\Delta \) and dP are displacement and load drop, respectively.

A part of this released energy transmits within the specimen in the form of stress waves [40, 48], and we record these waves as AE signals. Thus, the energy of the recorded AE signals (\(\Delta E_{{\textit{AE}}})\) is some proportion of the available elastic energy \((\Delta U)\) [48].

$$\begin{aligned} \Delta U\sim \Delta E_{{\textit{AE}}} \end{aligned}$$
(2)

Using Eq. (1), released strain energy at each pop-in was calculated. The corresponding AE energy jump at each pop-in was also calculated using the AE data recorded by the AE sensors. The obtained values of released strain energy (dU) and corresponded AE energy jump \((\hbox {dE}_{\mathrm{AE}})\) at each pop-in are represented in Tables 1 and 2.

Table 2 The values of released strain energy (dU) and AE energy jump \((\hbox {dE}_{\mathrm{AE}})\) at each pop-in for the \(\hbox {W}_{\mathrm{S1}}\) specimen
Full size table
Fig. 10
figure 10

Correlation between the AE energy jump and the strain energy drop at the pop-ins for the \(\hbox {U}_{\mathrm{S1}}\) and \(\hbox {W}_{\mathrm{S1}}\) specimens

Full size image
Fig. 11
figure 11

Correlation between visual crack growth and cumulative AE energy of delamination for the \(\hbox {U}_{\mathrm{S1}}\) and \(\hbox {W}_{\mathrm{S1}}\) specimens

Full size image

Figure 10 illustrates the correlation between the AE energy jump and the released strain energy at the pop-ins. In consistent with Eq. (2), there is a linear relationship between the AE energy jump and the released strain energy. Thus, amount of the AE energy, induced by the crack growth, is a function of the released strain energy.

Fig. 12
figure 12

Prediction of crack growth using the AE method for the \(\hbox {U}_{\mathrm{S1}}\) and \(\hbox {W}_{\mathrm{S1}}\) specimens

Full size image
Fig. 13
figure 13

Prediction of crack growth using the AE method for the \(\hbox {U}_{\mathrm{S2}}\) specimen

Full size image
Table 3 The maximum and average error of the AE crack growth prediction
Full size table
Table 4 The specifications of the cyclic loading tests
Full size table
Fig. 14
figure 14

The fatigue crack growth for the \(\hbox {U}_{\mathrm{F1}}\) and \(\hbox {W}_{\mathrm{F1}}\) specimens

Full size image

Strain energy release rate in mode I \((\hbox {G}_{\mathrm{I}})\) for a DCB specimen is calculated as follows [47]:

$$\begin{aligned} G_I =-\frac{1}{B}\left( {\frac{dU}{da}} \right) _\Delta =\frac{12P^{2}a^{2}}{{\textit{EB}}^{2}h^{3}} \end{aligned}$$
(3)

where B, P, a, E, U, and h are the specimen width, applied load, initial crack length, young modulus, released strain energy, and a half thickness of the specimen, respectively. Thus, the elastic strain energy (\(\Delta U)\) released due to growth of delamination length (\(\Delta a)\) is calculated as follows:

$$\begin{aligned} dU= & {} -\frac{12P^{2}a^{2}}{{\textit{EBh}}^{3}}{\textit{da}} \end{aligned}$$
(4)
$$\begin{aligned} \int \limits _0^{\Delta U} {dU}= & {} -\int \limits _a^{a+\Delta a} {\frac{12P^{2}a^{2}}{{\textit{EBh}}^{3}}da} \end{aligned}$$
(5)
$$\begin{aligned} \Delta U= & {} -\frac{4P^{2}}{{\textit{EBh}}^{3}}\left[ {(a+\Delta a)^{3}-a^{3}} \right] \nonumber \\= & {} \alpha P^{2}\left[ {(a+\Delta a)^{3}-a^{3}}\right] \end{aligned}$$
(6)

where \(\alpha =-\frac{4}{{\textit{EBh}}^{3}}\).

Fig. 15
figure 15

Cumulative AE energy curve for the \(\hbox {U}_{\mathrm{F1}}\) and \(\hbox {W}_{\mathrm{F1}}\) specimens

Full size image
Fig. 16
figure 16

Correlation between fatigue crack growth and cumulative AE energy for the \(\hbox {U}_{\mathrm{F1}}\) and \(\hbox {W}_{\mathrm{F1}}\) specimens

Full size image
Fig. 17
figure 17

Predicted and visually detected delamination fatigue crack growth for the \(\hbox {U}_{\mathrm{F1}}\) and \(\hbox {W}_{\mathrm{F1}}\) specimens

Full size image
Fig. 18
figure 18

Predicted and visually detected delamination fatigue crack growth for the \(\hbox {U}_{\mathrm{F2}}\) and \(\hbox {W}_{\mathrm{F2}}\) specimens

Full size image

According to the linear relation of Fig. 10, combining Eqs. (2) and (6) leads to

$$\begin{aligned} \Delta E_{{\textit{AE}}}= & {} \eta \bigg (\alpha P^{2}\left[ {(a+\Delta a)^{3}-a^{3}} \right] \bigg )+\gamma \nonumber \\= & {} \beta P^{2}\left[ {(a+\Delta a)^{3}-a^{3}} \right] +\gamma \end{aligned}$$
(7)

where \(\beta =\eta \alpha \). \(\eta \) and \(\gamma \) are the coefficients of the linear equation of Fig. 10. Using \(x^{3}-y^{3}=(x-y)(x^{2}+{\textit{xy}}+y^{2})\) substitution, Eq. (7) is modified as follows:

$$\begin{aligned} \Delta E_{{\textit{AE}}}= & {} \beta P^{2}\left[ {(a+\Delta a)^{3}-a^{3}} \right] +\gamma \nonumber \\= & {} \beta P^{2}\left[ {\Delta a^{3}+3a\Delta a^{2}+3a^{2}\Delta a} \right] +\gamma \end{aligned}$$
(8)

Finally, Eq. (8) can be written as a general form as follows:

$$\begin{aligned} E_{{\textit{AE}}} =A_1 \Delta a^{3}+A_2 \Delta a^{2}+A_3 \Delta a+A_4 \end{aligned}$$
(9)

where \(\hbox {A}_{1}\) to \(\hbox {A}_{4}\) are the constants of the 3rd degree polynomial equation.

Figure 11 shows the correlation between the cumulative crack growth and the cumulative AE energy of delamination for the \(\hbox {U}_{\mathrm{S1}}\) and \(\hbox {W}_{\mathrm{S1}}\) specimens. A 3rd degree polynomial has been fitted to the data. Due to the very high values of the R-square and the adjusted R-square for the fittings, it is concluded that the 3rd degree polynomial of Eq. (9) truly expresses the correlation between the\(E_{AE} \) and \(\Delta a\).

The real root of Eq. (9) at a specific cumulative AE energy determines the crack growth value. Figure 12 shows the delamination crack growth estimated by cumulative AE energy versus visually recorded experimental data. As it is obvious, there is an excellent agreement between the results. In order to qualify the performance of the proposed method in different loading condition, another unidirectional specimen were tested with 1 mm/min loading rate. Figure 13 shows the estimated delamination propagation curve versus the visually recorded curve for this specimen. As can be seen, by changing the loading condition, the AE method still can predict the delamination propagation precisely.

Table 3 represents the average and maximum differences between the predicted delamination crack growth by the AE method and the visually detected crack growth. The results show that the proposed AE method has a good performance to predict quasi-static delamination crack growth.

3.2 Fatigue Loading

In order to evaluate the performance of the proposed AE-based method in a complicated loading condition, the fatigue loading tests were carried out. Some samples identical with the quasi-static specimens were subjected to the fatigue loading. The specifications of the fatigue loading tests are represented in Table 4.

Fatigue crack growth curves for the \(\hbox {U}_{\mathrm{F1}}\) and \(\hbox {W}_{\mathrm{F1}}\) specimens are illustrated in Fig. 14. As can be seen, the fatigue crack growth in the \(\hbox {W}_{\mathrm{F1}}\) specimen is more stable than the \(\hbox {U}_{\mathrm{F1}}\) specimen. Similar to the quasi-static loading, instability of the fatigue crack growth in the \(\hbox {U}_{\mathrm{F1}}\) specimen refers to the fiber bridging phenomenon (see Fig. 4a).

Table 5 The maximum and average error of the AE fatigue crack growth prediction
Full size table

3.3 Prediction of Fatigue Crack Growth Using AE

Cumulative AE energy of the AE signals originated from the delamination damage for the \(\hbox {U}_{\mathrm{F1}}\) and \(\hbox {W}_{\mathrm{F1}}\) specimens are illustrated in Fig. 15. Figure 16 shows the correlation between cumulative fatigue crack growth and cumulative AE energy of delamination for these specimens. Similar to the correlation between delamination growth and cumulative AE energy in quasi-static loading, there is a 3rd degree polynomial correlation between the cumulative fatigue crack growth and the cumulative AE energy. Due to the very high values of R-square and the adjusted R-square for the fittings, it is concluded that the 3rd degree polynomial fitting truly expresses the correlation between the cumulative fatigue crack growth and the cumulative AE energy.

Figure 17 illustrates the predicted fatigue crack growth and visually recorded crack growth for the \(\hbox {U}_{\mathrm{F1}}\) and \(\hbox {W}_{\mathrm{F1}}\) specimens. The results show that this method could precisely predict the fatigue crack growth.

In order to qualify the performance of the proposed method for different fatigue loading conditions, the \(\hbox {U}_{\mathrm{F2}}\) and \(\hbox {W}_{\mathrm{F2}}\) specimens were tested under lower stress levels \(\left( \frac{\updelta _{\max }^2 }{\left[ {\updelta _{{ cr}} } \right] _{av}^2 }=\frac{G_{\mathrm{Imax} } }{G_{{ Ic}} }=0.5\right) \). The predicted fatigue crack growth curve for these specimens are illustrated in Fig. 18.

Table 5 represents the average and maximum differences between the predicted fatigue crack growth by the AE method and the visually detected fatigue crack growth. The results show that the proposed AE method has an excellent performance to predict the delamination fatigue crack growth.

4 Conclusion

The aim of this study was to investigate the delamination propagation in glass/epoxy composites under mode I quasi-static and fatigue loading conditions. The results are represented in two sections. In the first section, correlations among the AE energy with the released strain energy and the crack growth were established based on the theoretical fundamentals. It was shown that there is a 3rd degree polynomial correlation between the cumulative AE energy of delamination and the cumulative crack growth and accordingly the quasi-static delamination crack growth was predicted using the AE method. In the second section, the delamination crack growth under the fatigue loading is predicted using the proposed AE method. The proposed AE method has some advantages such as predicting delamination growth using only one AE sensor without a need to determine AE wave propagation velocity in the specimens. This method is a robust technique for detecting and measuring the crack length, especially when the crack is hidden and could not be seen visually.