Skip to main content
SpringerLink
Log in

Optimal-Order Convergence of a Two-Step BDF Method for the Navier–Stokes Equations with \(H^1\) Initial Data

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

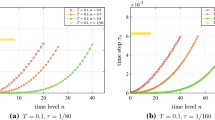
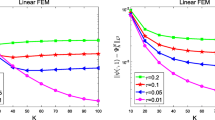
In this paper, we study the convergence of a fully discrete linearly extrapolated two-step backward difference time-stepping scheme, with finite element method in space, for the two-dimensional Navier–Stokes equations with \(H^1\) initial data (without any additional compatibility conditions), i.e., \(u_0\in [H_0^1(\Omega )]^2\), and \(\nabla \cdot u_0 = 0\). By using properly designed variable time stepsizes locally refined towards \(t=0\), we prove second-order convergence of the method in both time and space without any CFL conditions. Numerical examples are provided to illustrate the convergence of the method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availability

Enquiries about data availability should be directed to the authors.

References

  1. Adams, R.A., Fournier, J.J.F.: Sobolev Spaces. Pure and Applied Mathematics, vol. 140, 2nd edn. Elsevier, Amsterdam (2003)

    MATH  Google Scholar 

  2. Baker, G.A.: Galerkin Approximations for the Navier–Stokes Equations. Harvard University, Cambridge (1976)

    Google Scholar 

  3. Baker, G.A., Dougalis, V.A., Karakashian, O.A.: On a higher order accurate fully discrete Galerkin approximation to the Navier–Stokes equations. Math. Comput. 39(160), 339–375 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bermejo, R., Galán del Sastre, P., Saavedra, L.: A second order in time modified Lagrange–Galerkin finite element method for the incompressible Navier–Stokes equations. SIAM J. Numer. Anal. 50(6), 3084–3109 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  5. Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods. Texts in Applied Mathematics, vol. 5, 3rd edn. Springer, New York (2008)

    Book  MATH  Google Scholar 

  6. Emmrich, E.: Error of the two-step BDF for the incompressible Navier–Stokes problem. Math. Model. Numer. Anal. 38(5), 757–764 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  7. Emmrich, E.: Stability and error of the variable two-step BDF for semilinear parabolic problems. J. Appl. Math. Comput. 19(1–2), 33–55 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  8. Girault, V., Raviart, P.-A.: Finite Element Approximation of the Navier–Stokes Equations. Lecture Notes in Mathematics, vol. 749. Springer, Berlin (1979)

    Book  MATH  Google Scholar 

  9. Girault, V., Raviart, P.A.: Finite Element Methods for Navier–Stokes Equations: Theory and Algorithms. Springer Series in Computational Mathematics, vol. 5. Springer, Berlin (1986)

    Book  MATH  Google Scholar 

  10. Guo, Y., He, Y.: Unconditional convergence and optimal \(L^2\) error estimates of the Crank–Nicolson extrapolation FEM for the nonstationary Navier–Stokes equations. Comput. Math. Appl. 75(1), 134–152 (2018)

    MathSciNet  MATH  Google Scholar 

  11. He, Y.: The Euler implicit/explicit scheme for the 2D time-dependent Navier–Stokes equations with smooth or non-smooth initial data. Math. Comput. 77(264), 2097–2124 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  12. He, Y.: Stability and error analysis for spectral Galerkin method for the Navier–Stokes equations with \(L^2\) initial data. Numer. Methods Part. Differ. Equ. 24(1), 79–103 (2008)

    Article  MATH  Google Scholar 

  13. He, Y.: The Crank–Nicolson/Adams–Bashforth scheme for the time-dependent Navier–Stokes equations with nonsmooth initial data. Numer. Methods Part. Differ. Equ. 28(1), 155–187 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  14. He, Y., Li, K.: Convergence and stability of finite element nonlinear Galerkin method for the Navier–Stokes equations. Numer. Math. 79(1), 77–106 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  15. He, Y., Sun, W.: Stability and convergence of the Crank–Nicolson/Adams–Bashforth scheme for the time-dependent Navier–Stokes equations. SIAM J. Numer. Anal. 45(2), 837–869 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  16. Heywood, J.G., Rannacher, R.: Finite element approximation of the nonstationary Navier–Stokes problem. I. Regularity of solutions and second-order error estimates for spatial discretization. SIAM J. Numer. Anal. 19(2), 275–311 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  17. Heywood, J.G., Rannacher, R.: Finite element approximation of the nonstationary Navier–Stokes problem. IV. Error analysis for second-order time discretization. SIAM J. Numer. Anal. 27(2), 353–384 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  18. Hill, A.T., Süli, E.: Approximation of the global attractor for the incompressible Navier–Stokes equations. IMA J. Numer. Anal. 20(4), 633–667 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  19. Li, B., Ma, S., Ueda, Y.: Analysis of fully discrete finite element methods for 2D Navier–Stokes equations with critical initial data. ESAIM Math. Model. Numer. Anal. 56(6), 2105–2139 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  20. Li, B., Ma, S., Wang, N.: Second-order convergence of the linearly extrapolated Crank–Nicolson method for the Navier–Stokes equations with \(H^1\) initial data. J. Sci. Comput. 88(3), 20 (2021)

    Article  MATH  Google Scholar 

  21. Liao, H.-L., Zhang, Z.: Analysis of adaptive BDF2 scheme for diffusion equations. Math. Comput. 90(329), 1207–1226 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  22. Liu, W., Hou, Y., Xue, D.: Numerical analysis of a 4th-order time parallel algorithm for the time-dependent Navier–Stokes equations. Appl. Numer. Math. 150, 361–383 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  23. Notsu, H., Tabata, M.: Error estimates of a stabilized Lagrange–Galerkin scheme for the Navier–Stokes equations. ESAIM Math. Model. Numer. Anal. 50(2), 361–380 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  24. Rannacher, R., Scott, R.: Some optimal error estimates for piecewise linear finite element approximations. Math. Comput. 38(158), 437–445 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  25. Shen, J.: On error estimates of projection methods for Navier–Stokes equations: first-order schemes. SIAM J. Numer. Anal. 29(1), 57–77 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  26. Shen, J.: On error estimates of the projection methods for the Navier–Stokes equations: second-order schemes. Math. Comput. 65(215), 1039–1065 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  27. Tang, Q., Huang, Y.: Stability and convergence analysis of a Crank–Nicolson leap-frog scheme for the unsteady incompressible Navier–Stokes equations. Appl. Numer. Math. 124, 110–129 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  28. Temam, R.: Navier–Stokes Equations. Theory and Numerical Analysis. Studies in Mathematics and its Applications, vol. 2. North-Holland Publishing Company, Amsterdam (1977)

    MATH  Google Scholar 

  29. Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems. Springer Series in Computational Mathematics, vol. 2, 2nd edn. Springer, Berlin (2006)

    MATH  Google Scholar 

  30. Wang, K., Lv, C.: Third-order temporal discrete scheme for the non-stationary Navier–Stokes equations. Int. J. Comput. Math. 89(15), 1996–2018 (2012)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous referees for their valuable comments and suggestions.

Funding

The work of the authors was partially supported by grants from National Natural Science Foundation of China (Grants No. 12071020, 12131005, and U2230402).

Author information

Authors and Affiliations

  1. Beijing Computational Science Research Center, Beijing, 100193, China

    Tianyang Chu & Na Wang

  2. School of Science, Harbin Institute of Technology, Shenzhen, 518055, China

    Jilu Wang

  3. Department of Mathematics, Wayne State University, Detroit, MI, 48202, USA

    Zhimin Zhang

Authors
  1. Tianyang Chu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jilu Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Na Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zhimin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jilu Wang.

Ethics declarations

Conflict of interest

The authors have not disclosed any competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chu, T., Wang, J., Wang, N. et al. Optimal-Order Convergence of a Two-Step BDF Method for the Navier–Stokes Equations with \(H^1\) Initial Data. J Sci Comput 96, 62 (2023). https://doi.org/10.1007/s10915-023-02270-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02270-x

Keywords

Mathematics Subject Classification

Search

Navigation