Entropy Stable Discontinuous Galerkin Schemes on Moving Meshes for Hyperbolic Conservation Laws

Abstract

This work is focused on the entropy analysis of a semi-discrete nodal discontinuous Galerkin spectral element method (DGSEM) on moving meshes for hyperbolic conservation laws. The DGSEM is constructed with a local tensor-product Lagrange-polynomial basis computed from Legendre–Gauss–Lobatto points. Furthermore, the collocation of interpolation and quadrature nodes is used in the spatial discretization. This approach leads to discrete derivative approximations in space that are summation-by-parts (SBP) operators. On a static mesh, the SBP property and suitable two-point flux functions, which satisfy the entropy condition from Tadmor, allow to mimic results from the continuous entropy analysis, if it is ensured that properties such as positivity preservation (of the water height, density or pressure) are satisfied on the discrete level. In this paper, Tadmor’s condition is extended to the moving mesh framework. We show that the volume terms in the semi-discrete moving mesh DGSEM do not contribute to the discrete entropy evolution when a two-point flux function that satisfies the moving mesh entropy condition is applied in the split form DG framework. The discrete entropy behavior then depends solely on the interface contributions and on the domain boundary contribution. The interface contributions are directly controlled by proper choice of the numerical element interface fluxes. If an entropy conserving two-point flux is chosen, the interface contributions vanish. To increase the robustness of the discretization we use so-called entropy stable two-point fluxes at the interfaces that are guaranteed entropy dissipative and thus give a bound on the interface contributions in the discrete entropy balance. The remaining boundary condition contributions depend on the type of the considered boundary condition. E.g. for periodic boundary conditions that are of entropy conserving type, our methodology with the entropy conserving interface fluxes is fully entropy conservative and with the entropy stable interface fluxes is guaranteed entropy stable. The presented proof does not require any exactness of quadrature in the spatial integrals of the variational forms. As it is the case for static meshes, these results rely on the assumption that additional properties like positivity preservation are satisfied on the discrete level. Besides the entropy stability, the time discretization of the moving mesh DGSEM will be investigated and it will be proven that the moving mesh DGSEM satisfies the free stream preservation property for an arbitrary s-stage Runge–Kutta method, when periodic boundary conditions are used. The theoretical properties of the moving mesh DGSEM will be validated by numerical experiments for the compressible Euler equations with periodic boundary conditions.

1 Introduction

A lot of applications in engineering and physics require the approximation of conservation laws on time-dependent domains, e.g. domains with moving boundaries. For instance, moving mesh discontinuous Galerkin (DG) methods have been investigated in [5, 43, 52, 54]. In particular, moving mesh discontinuous Galerkin spectral element methods (DGSEM) have been constructed and analyzed in [37, 48, 64]. In the literature, there are also moving mesh methods with the capability to change the connectivity of the mesh, e.g. with finite volume (FV) methods [44, 57] and with a DG method [60]. Moving mesh finite difference methods were constructed in [1, 51], in [66] a moving mesh collocation method was constructed and in [27] a moving mesh continuous finite element method was constructed. In general, moving mesh methods are well suited to preserve motion related properties like the Galilean-invariance. These properties are necessary to describe physical processes like the formation of disc galaxies [45].

A common way to approximate conservation laws on time-dependent domains is to use the Arbitrary Lagrangian–Eulerian (ALE) approach [17]. In this approach the conservation law is transformed from the time-dependent domain onto a time-independent reference domain. The motion of the mesh on the physical domain is part of the transformation. Thus, the grid velocity field appears as a new quantity in the equation on the reference domain. On the one hand the ALE transformation simplifies the discretization, since a static mesh can be used in the reference domain. On the other hand, the new quantities in the equation on the reference domain complicate the discrete stability analysis, even in the linear case [37].

In this work, moving mesh DGSEM to solve non-linear, symmetrizable and hyperbolic systems of conservation laws are investigated. It is well known that symmetrizable systems are equipped with an entropy/entropy flux pair [26, 49]. For scalar conservation laws, entropy admissibility criteria provide the unique physically relevant weak solution [15, 39]. In general, entropy admissibility criteria are not enough to ensure well-posedness for systems of conservation laws [11]. Nevertheless, the entropy is an essential quantity to analyze systems of conservation laws. In particular, for gas dynamics a possible mathematical entropy is the scaled negative thermodynamic entropy which shows that the mathematical model correctly captures the second law of thermodynamics [2]. The entropy is conserved for smooth solutions of a conservation law and decays for discontinuous solutions [29, 59].

It is reasonable to construct numerical schemes for conservation laws which reflect the properties of the entropy on the discrete level. Tadmor [58] developed a discrete entropy criterion to construct a specific class of two-point flux functions for low-order finite difference (FD) and FV methods. FD/FV methods with these class of two-point flux functions preserve entropy on the discrete level. Moreover, these FV methods can be modified by adding dissipation to the numerical fluxes such that the entropy is decreasing for all times. Therefore, two-point fluxes with Tadmor’s discrete entropy condition are called entropy conservative fluxes. LeFloch et al. [40] gave a framework to construct high-order entropy conservative schemes in periodic domains. Fisher and Carpenter [20] combined this approach with summation-by-parts (SBP) operators and proved that two-point entropy conservative fluxes can be used to construct high-order schemes when the derivative approximations in space are SBP operators. A SBP operator provides a discrete analogue of the integration-by-parts formula [19, 22, 38]. It is worth to mention that the derivative matrix in the DGSEM provides a SBP operator, if the tensor-product Lagrange-polynomial basis is computed from Legendre–Gauss–Lobatto (LGL) points and interpolation and quadrature are collocated. Gassner et al. [23, 24] showed that split forms of the partial differential equations can be discretely recovered when specific choices of numerical volume fluxes in the flux form volume integral of Fisher and Carpenter are chosen. Thus, an entropy stable DGSEM can be constructed by the following building blocks:

• (1) The derivative matrix satisfies the SBP property.

• (2) There are two-point flux functions with Tadmor’s discrete entropy condition that can be extended to high-order in a split form DG framework.

This methodology has been used in the construction of high-order entropy stable DGSEM on quadrilateral/hexahedral elements, e.g. [4, 23, 61], or on triangular/tetrahedral elements, e.g. [6, 10, 13]. All these methods are provably entropy stable and the semi-discrete entropy analysis for them is based merely on the properties of the SBP operators and the assumptions that the time integration is exact. Additionally, properties like positivity preservation (of the water height, density or pressure) must be satisfied on the discrete level. The exactness of quadrature in the spatial integrals of the variational form is not necessary. Available entropy stable moving mesh methods are for instance the low order continuous finite element method by Guermond et al. [27] and a spectral collocation based approach published during the extended review process of the current paper by Yamaleev et al. [66].

The remainder of the paper is organized as follows: The ALE transformation and continuous entropy analysis is presented in the Sects. 2.1, 2.2 and 2.3. The framework for the spectral element discretization with the SBP operator is given in the Sect. 2.4 and the DG split form framework is presented in the Sect. 2.5. The moving mesh DGSEM is finally presented in the Sect. 2.5. A discrete entropy analysis for the moving mesh DGSEM is given in the Sects. 2.6 and 2.7. Furthermore, in Sect. 2.8 it is proven that the moving mesh DGSEM satisfies the free stream preservation property. In Sect. 4, numerical examples with the compressible Euler equations are presented to validate our theoretical findings.

2 Entropy Stable DGSEM on Moving Meshes

The main goal of this work is the construction of an entropy stable moving mesh DGSEM. On static meshes, it is possible to construct high-order entropy stable DGSEM, if the derivative matrix is an SBP operator and entropy conservative two-point flux functions are available. This methodology has been used in the construction of high-order entropy stable DGSEM on quadrilateral/hexahedral elements, e.g. [4, 23, 61]. In this section, it will be shown that similar ideas can be used to construct high-order entropy stable moving mesh DGSEM. The construction of the entropy stable moving mesh DGSEM will be presented for an arbitrary symmetrizable and hyperbolic system of conservation laws

$$\begin{aligned} \frac{\partial \mathbf{u} }{\partial t}+\sum _{i=1}^{3}\frac{\partial \mathbf{f} _{i}}{\partial x_{i}}=\mathbf 0 , \end{aligned}$$

(2.1)

on a time-dependent domain $\Omega \left( t\right) \subseteq {\mathbb {R}}^3$. The vector of conservative variables is $\mathbf{u}$ and $\mathbf{f} _i,\,i=1,2,3$, are the physical flux vectors. The state vectors are of size p depending on the number of equations in the system under consideration and the conservation law is subjected to appropriate initial and boundary conditions (see the comment below Eq. (2.44) in Sect. 2.3).

The block vector nomenclature in [24] simplifies the analysis of the system (2.1) on curved elements. Thus, we translate the conservation law (2.1) in block vector notation. A block vector is highlighted by the double arrow

$$\begin{aligned} {\overset{\leftrightarrow }{\mathbf{f }}}:=\begin{bmatrix} {\mathbf {f}}_{1} \\ {\mathbf {f}}_{2} \\ {\mathbf {f}}_{3} \end{bmatrix}. \end{aligned}$$

(2.2)

The dot product of two block vectors is given by

$$\begin{aligned} {\overset{\leftrightarrow }{\mathbf{f }}}\cdot {\overset{\leftrightarrow }{\mathbf{g }}}:=\sum _{i=1}^{3} \mathbf{f} _{i}^{T}{} \mathbf{g} _{i}. \end{aligned}$$

(2.3)

Furthermore, the dot product of a vector $\vec {v}$ in the three dimensional space and a block vector is defined by

$$\begin{aligned} \vec {v}\cdot {\overset{\leftrightarrow }{\mathbf{f }}}:=\sum _{i=1}^{3}v_{i}{} \mathbf{f} _{i}. \end{aligned}$$

(2.4)

We note that the dot product (2.3) is a scalar quantity and the dot product (2.4) is a vector in a p dimensional space, where the number p corresponds to the number of conservative variables in the conservation law (2.1). The interaction between a vector $\vec {v}$ and the conservative variables is defined as the block vector

$$\begin{aligned} \vec {v}\,\mathbf{u} :=\begin{bmatrix}v_{1}{\mathbf {u}}\\ v_{2}{\mathbf {u}}\\ v_{3}{\mathbf {u}} \end{bmatrix}. \end{aligned}$$

(2.5)

Thus, in particular, the spatial gradient of the conservative variables is defined by

$$\begin{aligned} \vec {\nabla }_{x}{\mathbf {u}}:=\begin{bmatrix}\frac{\partial {\mathbf {u}}}{\partial x_{1}}\\ \frac{\partial {\mathbf {u}}}{\partial x_{2}}\\ \frac{\partial {\mathbf {u}}}{\partial x_{3}} \end{bmatrix}. \end{aligned}$$

(2.6)

The gradient of a vector valued function $\vec {g}=[g_{1},g_{2},g_{3}]^T$ is a second order tensor, written in matrix form as

$$\begin{aligned} \left[ \vec {\nabla }_{x}\otimes \vec {g}\right] ^{T}=\begin{bmatrix} \frac{\partial g_{1}}{\partial x_{1}} &{}\quad \frac{\partial g_{1}}{\partial x_{2}} &{} \quad \frac{\partial g_{1}}{\partial x_{3}}\\ \frac{\partial g_{2}}{\partial x_{1}} &{}\quad \frac{\partial g_{2}}{\partial x_{2}} &{} \quad \frac{\partial g_{2}}{\partial x_{3}}\\ \frac{\partial g_{3}}{\partial x_{1}} &{}\quad \frac{\partial g_{3}}{\partial x_{2}} &{}\quad \frac{\partial g_{3}}{\partial x_{3}} \end{bmatrix}, \end{aligned}$$

(2.7)

where $\otimes$ is the outer product of two vectors in a three dimensional space. The dot product (2.3) and the spatial gradient (2.6) are used to define the divergence of a block vector flux as

$$\begin{aligned} \vec {\nabla }_{x}\cdot {\overset{\leftrightarrow }{\mathbf{f }}}:=\sum _{i=1}^{3} \frac{\partial \mathbf{f} _{i}}{\partial x_{i}}. \end{aligned}$$

(2.8)

Moreover, for a vector valued function $\vec {g}$ and the conservative variables, we have the product rule

$$\begin{aligned} \vec {\nabla }_{x}\cdot \left( \vec {g}\,{\mathbf {u}}\right) =\left( \vec {\nabla }_{x} \cdot \vec {g}\right) {\mathbf {u}}+\vec {g}\cdot \left( \vec {\nabla }_{x}{\mathbf {u}}\right) \end{aligned}$$

(2.9)

with respect to the dot products (2.3) and (2.4). These notations allow to write the conservation law (2.1) in the compact form

$$\begin{aligned} \frac{\partial \mathbf{u} }{\partial t} + \vec {\nabla }_x\cdot {\overset{\leftrightarrow }{\mathbf{f }}} = \mathbf 0 . \end{aligned}$$

(2.10)

2.1 Building Blocks of the ALE Transformation for Hexahedral Curved Meshes

In order to set up the moving mesh DGSEM in the Sect. 2.5, we make for all $t\in \left[ 0,T\right]$ the assumptions:

• (A1) For a fixed number $K\in {\mathbb {N}}$ the physical domain $\Omega \left( t\right)$ can be subdivided into K time-dependent, non-overlapping and conforming hexahedral elements, $e_{\kappa }(t)$, $\kappa =1,\dots ,K$. These elements can have curved faces.

• (A2) The time-dependent elements $e_{\kappa }(t)$ are mapped into the spatial computational domain $E=\left[ -1,1\right] ^{3}$ with a bijective isoparametric transfinite mapping

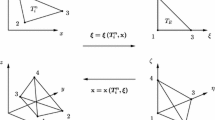
  $$\begin{aligned} e_{\kappa }\left( t\right) \ni \vec {x}\left( t\right) =\vec {\chi }\left( \vec {\xi }, \tau \right) ,\quad \vec {\xi }\in E,\quad \tau \in \left[ 0,T\right] . \end{aligned}$$

  (2.11)

  Winters constructed in his PHD thesis [65] a mapping for this set up. Like in [65], it is assumed that the curved faces satisfy for all $\tau \in \left[ 0,T\right]$

  $$\begin{aligned} \vec {\Gamma }_{1}\left( -1,\xi ^{3},\tau \right)&=\vec {\Gamma }_{6} \left( -1,\xi ^{3},\tau \right) , \vec {\Gamma }_{2}\left( -1,\xi ^{3},\tau \right) =\vec {\Gamma }_{6} \left( 1,\xi ^{3},\tau \right) ,\nonumber \\ \vec {\Gamma }_{3}\left( -1,\xi ^{2},\tau \right)&=\vec {\Gamma }_{6} \left( \xi ^{2},-1,\tau \right) ,\nonumber \\ \vec {\Gamma }_{1}\left( 1,\xi ^{3},\tau \right)&=\vec {\Gamma }_{4} \left( -1,\xi ^{3},\tau \right) , \vec {\Gamma }_{2}\left( 1,\xi ^{3},\tau \right) =\vec {\Gamma }_{4}\left( 1,\xi ^{3},\tau \right) , \nonumber \\ \vec {\Gamma }_{3} \left( 1,\xi ^{2},\tau \right)&=\vec {\Gamma }_{4}\left( \xi ^{2},-1,\tau \right) , \nonumber \\ \vec {\Gamma }_{1}\left( \xi ^{1},-1,\tau \right)&=\vec {\Gamma }_{3} \left( \xi ^{1},-1,\tau \right) , \vec {\Gamma }_{2} \left( \xi ^{1},-1,\tau \right) =\vec {\Gamma }_{3}\left( \xi ^{1},1,\tau \right) , \nonumber \\ \vec {\Gamma }_{5}\left( -1,\xi ^{2},\tau \right)&=\vec {\Gamma }_{6} \left( \xi ^{2},1,\tau \right) , \nonumber \\ \vec {\Gamma }_{1}\left( \xi ^{1},1,\tau \right)&=\vec {\Gamma }_{5} \left( \xi ^{1},-1,\tau \right) , \vec {\Gamma }_{2}\left( \xi ^{1},1,\tau \right) =\vec {\Gamma }_{5}\left( \xi ^{1},1,\tau \right) , \nonumber \\ \vec {\Gamma }_{5}\left( 1,\xi ^{2},\tau \right)&=\vec {\Gamma }_{4} \left( \xi ^{2},1,\tau \right) . \end{aligned}$$

  (2.12)

  The location of the curved faces is sketched in Fig. 1. The curved faces of an element $e_{\kappa }(t)$ are approximated as interpolation polynomials up to degree N such that

  $$\begin{aligned} {\mathbb {I}}^{N}\!\left( \vec {\Gamma }_{i}\right) \left( \eta ,\zeta ,\tau \right) :=\sum _{j,k=0}^{N}\vec {\Gamma }_{i}\left( \eta _{j},\zeta _{k},\tau \right) \ell _{j}\left( \eta \right) \ell _{k}\left( \zeta \right) ,\quad i=1,2,3,4,5,6, \end{aligned}$$

  (2.13)

  where $\left\{ \ell _{j}\right\} _{j=0}^{N}$, $\left\{ \ell _{k}\right\} _{k=0}^{N}$ are the Lagrange polynomials associated with the interpolation points $\left\{ \eta _{j}\right\} _{j=0}^{N}$ and $\left\{ \zeta _{k}\right\} _{k=0}^{N}$.

• (A3) The determinant J of the Jacobian matrix $\left[ \vec {\nabla }_{\vec {\xi }}\otimes \vec {\chi }\right] ^{T}$ satisfies

  $$\begin{aligned} J:=\text {det}\left( \vec {\nabla }_{\vec {\xi }}\otimes \vec {\chi }\right) >0, \quad \forall \tau \in \left[ 0,T\right] . \end{aligned}$$

  (2.14)

Mesh curving techniques are discussed by Hindenlang et al. [30] and methodologies to construct a moving mesh with the properties (A1)–(A3) are given in the literature e.g. the book of Huang and Russell [32, Chapter 6, Chapter 7]. In many situations the moving mesh methodology depends on the underlying problem, e.g. [45].

Fig. 1

Left the reference element $E=[-1,1]^3$ and on the right a general hexahedral element $e_{\kappa }(t)$ with the curved faces $\vec {\Gamma }_{1}\left( \xi ^{1},\xi ^{3},\tau \right)$, $\vec {\Gamma }_{2}\left( \xi ^{1},\xi ^{3},\tau \right)$, $\vec {\Gamma }_{3}\left( \xi ^{1},\xi ^{2},\tau \right)$, $\vec {\Gamma }_{4}\left( \xi ^{2},\xi ^{3},\tau \right)$, $\vec {\Gamma }_{5}\left( \xi ^{1},\xi ^{2},\tau \right)$, and $\vec {\Gamma }_{6}\left( \xi ^{2},\xi ^{3},\tau \right)$. The mapping $\vec {x}\left( t\right) =\vec {\chi }\left( \vec {\xi },\tau \right)$ connects E and $e_{\kappa }(t)$

The mapping provides the grid velocity field

$$\begin{aligned} \vec {\nu }=\left[ \nu _{1},\nu _{2},\nu _{3}\right] ^{T}:= \left[ \frac{\partial \chi _{1}}{\partial \tau },\frac{\partial \chi _{2}}{\partial \tau }, \frac{\partial \chi _{3}}{\partial \tau }\right] ^{T}=\frac{\partial \vec {\chi }}{\partial \tau }. \end{aligned}$$

(2.15)

It is desirable that the grid velocity is continuous, since the mesh should be conforming and watertight at each time level. The next statement provides conditions on the element boundaries to guarantee that the grid velocity becomes continuous.

Lemma 2.1

Let $e_{1}(t)$ and $e_{2}(t)$ be two neighboring elements which share one of the faces

$$\begin{aligned} \vec {\Gamma }_{1}^{1}=\vec {\Gamma }_{2}^{2},\quad \vec {\Gamma }_{3}^{1} =\vec {\Gamma }_{5}^{2},\quad \vec {\Gamma }_{4}^{1}=\vec {\Gamma }_{6}^{2}, \quad \vec {\Gamma }_{1}^{2}=\vec {\Gamma }_{2}^{1},\quad \vec {\Gamma }_{3}^{2} =\vec {\Gamma }_{5}^{1},\quad \vec {\Gamma }_{4}^{2}=\vec {\Gamma }_{6}^{1}, \end{aligned}$$

(2.16)

where $\vec {\Gamma }_{i}^{l}$, $l=1,2$, and $i=1,2,3,4,5,6$, are the faces of the element $e_{l}(t)$. Furthermore, suppose that the faces $\vec {\Gamma }_{i}^{l}\left( \cdot ,\cdot ,\tau \right)$ are continuously differentiable in the time interval $\left[ 0,T\right]$. Then the grid velocity field is continuous in the points which belong to the face that the elements share.

In Appendix A the Lemma 2.1 is proven in two dimensions. The three dimensional proof can be done by the same argumentation.

2.2 Transformation of the Conservation Law onto a Reference Element

In the following, we show that the system (2.10) can be transformed from a time-dependent element $e_{\kappa }(t)$ on the reference element E. The mapping (A.1) provides the covariant basis vectors

$$\begin{aligned} \vec {a}_{i}:=\frac{\partial \vec {\chi }}{\partial \xi ^{i}},\quad i=1,2,3, \end{aligned}$$

(2.17)

and the volume weighted contravariant vectors

$$\begin{aligned} J\vec {a}^{i}=\vec {a}_{j}\times \vec {a}_{k}, \quad (i, j, k) \ \text {cyclic}. \end{aligned}$$

(2.18)

The quantity $\vec {\xi }=\left( \xi ^{1},\xi ^{2},\xi ^{3}\right) ^{T}$ is a vector in the reference element $E=[-1,1]^3$. The covariant and the volume weighted contravariant vectors represent the Jacobian matrix $\left[ \vec {\nabla }_{\vec {\xi }}\otimes \vec {\chi }\right] ^{T}$ and its adjoint matrix

$$\begin{aligned} \left[ \vec {\nabla }_{\vec {\xi }}\otimes \vec {\chi }\right] ^{T}=\begin{bmatrix}\vec {a}_{1}&\vec {a}_{2}&\vec {a}_{3} \end{bmatrix},\quad \text {adj}\left( \left[ \vec {\nabla }_{\vec {\xi }}\otimes \vec {\chi }\right] ^{T}\right) =\begin{bmatrix}\left( J\vec {a}^{1}\right) ^{T}\\ \left( J\vec {a}^{2}\right) ^{T} \\ \left( J\vec {a}^{3} \right) ^{T} \end{bmatrix}. \end{aligned}$$

(2.19)

Furthermore, the contravariant vectors satisfy the metric identities

$$\begin{aligned} \sum _{i=1}^{3}\frac{\partial J\vec {a}^{i}}{\partial \xi ^{i}}=0. \end{aligned}$$

(2.20)

In particular, the covariant and the contravariant vectors allow to transform differential operators on the time-independent reference element E. On the reference element the gradient of a function f is given by

$$\begin{aligned} \vec {\nabla }_{x}f=\frac{1}{J}\left( \sum _{i=1}^{3}J\vec {a}^{i} \frac{\partial f}{\partial \xi ^{i}}\right) =\frac{1}{J}\left[ \text {adj} \left( \vec {\nabla }_{\vec {\xi }}\otimes \vec {\chi }\right) \right] \,\vec {\nabla }_{\xi }f \end{aligned}$$

(2.21)

and the divergence of a vector valued function $\vec {g}$ is given by

$$\begin{aligned} \vec {\nabla }_{x}\cdot \vec {g}=\frac{1}{J}\sum _{i=1}^{3}\frac{\partial }{\partial \xi ^{i}} \left( J\vec {a}^{i}\cdot \vec {g}\right) =\frac{1}{J} \vec {\nabla }_{\xi }\cdot \vec {\tilde{g}}, \end{aligned}$$

(2.22)

where we used the contravariant flux

$$\begin{aligned} \vec {\tilde{g}}:=\begin{bmatrix}J\vec {a}^{1}\cdot \vec {g}\\ J\vec {a}^{2}\cdot \vec {g}\\ J\vec {a}^{3}\cdot \vec {g} \end{bmatrix}=\left[ \text {adj}\left( \vec {\nabla }_{\vec {\xi }}\otimes \vec {\chi }\right) \right] ^{T}\,\vec {g}. \end{aligned}$$

(2.23)

In [24], the following block matrix has been introduced to combine the transformations (2.21) and (2.22) with the block vector notation

$$\begin{aligned} \varvec{\mathcal {M}}=\left[ \begin{matrix}Ja_{1}^{1}\mathcal {\mathcal {I_{\textit{p}}}} &{}\quad Ja_{1}^{2} \mathcal {\mathcal {I_{\textit{p}}}} &{}\quad Ja_{1}^{3}\mathcal {\mathcal {I_{\textit{p}}}}\\ Ja_{2}^{1}\mathcal {\mathcal {I_{\textit{p}}}} &{}\quad Ja_{2}^{2}\mathcal {\mathcal {I_{\textit{p}}}} &{}\quad Ja_{2}^{3} \mathcal {\mathcal {I_{\textit{p}}}}\\ Ja_{3}^{1}\mathcal {\mathcal {I_{\textit{p}}}} &{}\quad Ja_{3}^{2}\mathcal {\mathcal {I_{\textit{p}}}} &{}\quad Ja_{3}^{3} \mathcal {\mathcal {I_{\textit{p}}}} \end{matrix}\right] , \end{aligned}$$

(2.24)

where the matrix $\mathcal {\mathcal {I_{\textit{p}}}}$ is the $p\times p$ identity matrix and $Ja_{j}^{i}$ is the component of $J \vec {a}^{i}$ in the j-th Cartesian coordinate direction. The transformation of the gradient becomes

$$\begin{aligned} \vec {\nabla }_{x}{\mathbf {u}}=\frac{1}{J}\varvec{\mathcal {M}}\,\vec {\nabla }_{\xi }{\mathbf {u}}. \end{aligned}$$

(2.25)

We note that for a vector valued function $\vec {g}$ the following identity holds

$$\begin{aligned} \vec {g}\cdot \vec {\nabla }_{x}{\mathbf {u}}=\frac{1}{J}\vec {g}\cdot \varvec{\mathcal {M}}\,\vec {\nabla }_{\xi }{\mathbf {u}}=\frac{1}{J}\vec {\tilde{g}} \cdot \vec {\nabla }_{\xi }{\mathbf {u}}. \end{aligned}$$

(2.26)

Moreover, by applying the metric identities (2.20), the transformation of the divergence can be written as

$$\begin{aligned} \vec {\nabla }_{x}\cdot {\overset{\leftrightarrow }{\mathbf{f }}}=\frac{1}{J}\vec {\nabla }_{\xi } \cdot \varvec{\mathcal {M}}^{T}{\overset{\leftrightarrow }{\mathbf{f }}}. \end{aligned}$$

(2.27)

Hence, the contravariant block vector flux is given by

$$\begin{aligned} {\overset{\leftrightarrow }{\tilde{\mathbf{f }}}} := \begin{bmatrix}J\vec {a}^{1}\cdot {\overset{\leftrightarrow }{\mathbf{f }}}\\ J\vec {a}^{2}\cdot {\overset{\leftrightarrow }{\mathbf{f }}} \\ J\vec {a}^{3}\cdot {\overset{\leftrightarrow }{\mathbf{f }}} \end{bmatrix} =\varvec{\mathcal {M}}^{T}{\overset{\leftrightarrow }{\mathbf{f }}}. \end{aligned}$$

(2.28)

Since the elements $\left\{ e_{k}\left( t\right) \right\} _{k=1}^{K}$ are time-dependent, the time evolution of the quantity J needs to be analyzed. Thus, we apply Jacobi’s formula (cf. e.g. Bellman [3]) and obtain by (2.15), (2.19)

$$\begin{aligned} \begin{aligned} \frac{\partial J}{\partial \tau }=\text {tr}\left[ \left[ \text {adj}\left( \vec {\nabla }_{\vec {\xi }} \otimes \vec {\chi }\right) \right] ^{T}\frac{\partial }{\partial \tau }\left[ \vec {\nabla } \otimes \vec {\chi }\right] ^{T}\right] =\sum _{i=1}^{3}J\vec {a}^{i}\cdot \left( \frac{\partial \vec {a}_{i}}{\partial \tau }\right) =\sum _{i=1}^{3}J\vec {a}^{i}\cdot \left( \frac{\partial \vec {\nu }}{\partial \xi ^{i}}\right) , \end{aligned} \end{aligned}$$

(2.29)

where $\text {tr}\left[ \cdot \right]$ denotes the trace of a matrix. The metric identities (2.20) allow to write the Eq. (2.29) in conservation form

$$\begin{aligned} \frac{\partial J}{\partial \tau }=\sum _{i=1}^{3}\frac{\partial }{\partial \xi _{i}}\left( J\vec {a}^{i} \cdot \vec {\nu }\right) =\vec {\nabla }_{\xi }\cdot \vec {{\tilde{\nu }}}. \end{aligned}$$

(2.30)

The chain rule formula and the identity (2.26) provide

$$\begin{aligned} \frac{\partial {\mathbf {u}}}{\partial \tau }=\frac{\partial {\mathbf {u}}}{\partial t}+\frac{1}{J} \vec {{\tilde{\nu }}}\cdot \vec {\nabla }_{\xi }{\mathbf {u}}. \end{aligned}$$

(2.31)

Next, we plug (2.30) into Eq. (2.31), apply the product rule (2.9) and rearrange. This provides the equation

$$\begin{aligned} J\frac{\partial {\mathbf {u}}}{\partial t}=\frac{\partial \left( J{\mathbf {u}}\right) }{\partial \tau }- \vec {\nabla }_{\xi }\cdot \left( \vec {{\tilde{\nu }}}{\mathbf {u}}\right) . \end{aligned}$$

(2.32)

Finally, we combine the identities (2.27) and (2.32) to write the the conservation law (2.10) in the following form

$$\begin{aligned} \frac{\partial \left( J{\mathbf {u}}\right) }{\partial \tau }+\vec {\nabla }_{\xi }\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {g}}}}=\mathbf 0 , \end{aligned}$$

(2.33)

where

$$\begin{aligned} \overset{\leftrightarrow }{{\mathbf {g}}}= \begin{bmatrix}{\mathbf {g}}_{1}\\ {\mathbf {g}}_{2}\\ {\mathbf {g}}_{3}\\ \end{bmatrix} :=\begin{bmatrix}{\mathbf {f}}_{1}-\nu _{1}{\mathbf {u}}\\ {\mathbf {f}}_{2}-\nu _{2}{\mathbf {u}} \\ {\mathbf {f}}_{3}-\nu _{3}{\mathbf {u}} \end{bmatrix}=\overset{\leftrightarrow }{{\mathbf {f}}}-\vec {\nu }{\mathbf {u}}. \end{aligned}$$

(2.34)

The formulation (2.33) is the representation of the system (2.10) on the time-independent reference element E for a time-dependent element $e_{\kappa }(t)$.

Remark 2.2

The metric identities (2.20) and the Eq. (2.30) provide the geometric conservation law (GCL) [18, 28, 41, 42, 46]. A numerical method to solve (2.10) on moving and deforming grids needs to satisfy both equations, otherwise the conservation properties of the conservation law (2.10) are not preserved. Farhat et al. [18, 28, 41] proved that the absence of these equations has a critical effect on the accuracy and stability of a moving mesh method. In particular, the preservation of constant states is no longer guaranteed, if the GCL is not satisfied on the discrete level.

2.3 Entropy Analysis in Three Dimensions

The system (2.1) is assumed to be symmetrizable. Thus, in particular, it is equipped with entropy/entropy flux pairs $\left( s,f_{i}^{s}\right)$, $i=1,2,3$, (cf. Godunov [26] and Mock [49]). The strictly convex function s is the entropy function. The entropy function s provides the entropy variables

$$\begin{aligned} \mathbf{w} :=\frac{\partial s}{\partial \mathbf{u} }, \end{aligned}$$

(2.35)

and it follows by the chain rule

$$\begin{aligned} \frac{\partial s}{\partial t}={\mathbf {w}}^{T}\frac{\partial {\mathbf {u}}}{\partial t},\quad \frac{\partial s}{\partial x_{i}}={\mathbf {w}}^{T}\frac{\partial {\mathbf {u}}}{\partial x_{i}}, \quad i=1,2,3. \end{aligned}$$

(2.36)

The entropy flux functions and the flux functions in the conservation law are related and satisfy

$$\begin{aligned} {\mathbf {w}}^{T}\frac{\partial {\mathbf {f}}_{i}}{\partial x_{i}}=\frac{\partial f_{i}^{s}}{\partial x_{i}}, \quad i=1,2,3. \end{aligned}$$

(2.37)

The identities (2.26) and (2.36) give

$$\begin{aligned} {\mathbf {w}}^{T}\left( \vec {{\tilde{\nu }}}\cdot \vec {\nabla }_{\xi }{\mathbf {u}}\right) =J{\mathbf {w}}^{T}\left( \vec {\nu }\cdot \vec {\nabla }_{x}{\mathbf {u}}\right) =J \left( \vec {\nu }\cdot \vec {\nabla }_{x}s\right) =\vec {{\tilde{\nu }}}\cdot \vec {\nabla }_{\xi }s. \end{aligned}$$

(2.38)

Hence, we obtain with the identity (2.31) and the chain rule

$$\begin{aligned} J{\mathbf {w}}^{T}\frac{\partial {\mathbf {u}}}{\partial \tau }=J\frac{\partial s}{\partial t}+ \vec {{\tilde{\nu }}}\cdot \vec {\nabla }_{\xi }s=J\frac{\partial s}{\partial \tau }. \end{aligned}$$

(2.39)

Therefore, the product rule provides the identity

$$\begin{aligned} \begin{aligned} {\mathbf {w}}^{T}\frac{\partial \left( J{\mathbf {u}}\right) }{\partial \tau }&= J\frac{\partial s}{\partial \tau }+\left( \frac{\partial J}{\partial \tau }\right) {\mathbf {w}}^{T}{\mathbf {u}} \\&= \frac{\partial \left( Js\right) }{\partial \tau }+\left( \frac{\partial J}{\partial \tau } \right) \left( {\mathbf {w}}^{T}{\mathbf {u}}-s\right) \\&= \frac{\partial \left( Js\right) }{\partial \tau }+\left( \vec {\nabla }_{\xi } \cdot \vec {{\tilde{\nu }}}\right) \left( {\mathbf {w}}^{T}{\mathbf {u}}-s\right) , \end{aligned} \end{aligned}$$

(2.40)

where we used the GCL (2.30) in the last step. Next, we apply the relation (2.37) for the entropy flux functions and obtain

$$\begin{aligned} {\mathbf {w}}^{T}\frac{\partial {\mathbf {g}}_{i}}{\partial x_{i}}=\frac{\partial }{\partial x} \left( f_{i}^{s}-\nu _{i}s\right) -\left( \frac{\partial v_{i}}{\partial x_{i}}\right) \left( {\mathbf {w}}^{T}{\mathbf {u}}-s\right) ,\quad i=1,2,3. \end{aligned}$$

(2.41)

Next, we apply the vector notation $\vec {f}^{s}:=\left[ f_{1}^{s},f_{2}^{s},f_{3}^{s}\right] ^{T}$. Then (2.41) and the transformation formulas for the gradient and divergence in the Sect. 2.2 give

$$\begin{aligned} {\mathbf {w}}^{T}\left( \vec {\nabla }_{\xi }\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {g}}}}\right) =\vec {\nabla }_{\xi }\cdot \left( \vec {\tilde{f}}{{}^{s}}-\vec {{\tilde{\nu }}}s\right) - \left( \vec {\nabla }_{\xi }\cdot \vec {{\tilde{\nu }}}\right) \left( {\mathbf {w}}^{T}{\mathbf {u}}-s\right) . \end{aligned}$$

(2.42)

Finally, the identities (2.40) and (2.42) provide the balance law

$$\begin{aligned} 0={\mathbf {w}}^{T}\left( \frac{\partial \left( J{\mathbf {u}}\right) }{\partial \tau }+\vec {\nabla }_{\xi } \cdot \overset{\leftrightarrow }{\tilde{{\mathbf {g}}}}\right) =\frac{\partial \left( Js\right) }{\partial \tau } +\vec {\nabla }_{\xi }\cdot \left( \vec {\tilde{f}}{{}^{s}}-\vec {{\tilde{\nu }}}s\right) . \end{aligned}$$

(2.43)

We integrate the Eq. (2.43) over the domain $E\times \left[ 0,T\right]$ and obtain

$$\begin{aligned} \frac{\partial }{\partial \tau }\int \int _{E}Js\,d\vec {\xi }\,d\tau =-\int _{0}^{T} \int _{\partial E}\left( \vec {\tilde{f}}{{}^{s}}-\vec {{\tilde{\nu }}}s\right) ^{T}{\hat{n}}\,dS\,d\tau . \end{aligned}$$

(2.44)

Boundary conditions then need to be specified so that the bound on the entropy depends only on the boundary data. We will assume here that boundary data is given in a way that the right hand side in Eq. (2.44) is non-positive so that the entropy will not increase in time.

For discontinuous solutions the Eq. (2.44) is not satisfied, but under further assumptions it is possible to proof that a weak solution of (2.33) satisfies the inequality

$$\begin{aligned} \frac{\partial \left( Js\right) }{\partial \tau }+\vec {\nabla }_{\xi }\cdot \left( \vec {\tilde{f}}{{}^{s}}-\vec {{\tilde{\nu }}}s\right) \le 0 \end{aligned}$$

(2.45)

in the sense of distributions on $E\times \left( 0,T\right)$ (see Godlewski and Raviart [25, Chapter 1, Theorem 3.3]). The inequality (2.45) means that it holds the inequality

$$\begin{aligned} \int _{0}^{T}\int _{E}Js\frac{\partial \phi }{\partial \tau }\,d\vec {\xi }\,d\tau \ge - \int _{0}^{T}\int _{E} \left( \vec {\tilde{f}}{{}^{s}}-\vec {{\tilde{\nu }}}s\right) ^{T} \vec {\nabla }_{\xi }\phi \,d\vec {\xi }\,d\tau ,\quad \forall \phi \in { \mathcal {C}}_{0}^{\infty }\left( E\times \left( 0,T\right) \right) ,\quad \phi \ge 0.\nonumber \\ \end{aligned}$$

(2.46)

2.4 Building Blocks for the Spectral Element Approximation

A nodal approach is used for the spectral element approximation. The Lagrange basis functions are given by

$$\begin{aligned} \ell _{j}\left( \xi \right) :=\prod _{i=0,\,j\ne i}^{N}\frac{\xi -\xi _{i}}{\xi _{j}-\xi _{i}},\quad j=0,\dots N, \end{aligned}$$

(2.47)

where the nodal points $\left\{ \xi _{i}\right\} _{i=0}^{N}$ are the LGL points. We note that $\xi _{0}=-1$ and $\xi _{N}=1$. The Lagrange basis functions satisfy the cardinal property

$$\begin{aligned} \ell _{i}\left( \xi _{j}\right) =\delta _{ji}, \end{aligned}$$

(2.48)

where $\delta _{ji}$ is the Kronecker delta. On the reference element $E=\left[ -1,1\right] ^{3}$ the solution and fluxes of the system (2.33) are approximated by tensor product Lagrange polynomials of degree N, e.g.

$$\begin{aligned} {\mathbf {u}}\left( \xi ^{1},\xi ^{2},\xi ^{3},t\right) \approx {\mathbf {U}}\left( \xi ^{1},\xi ^{2},\xi ^{3},t\right) := \sum _{i,j,k=0}^{N}{\mathbf {U}}_{ijk}\left( t\right) \ell _{i}\left( \xi ^{1}\right) \ell _{j}\left( \xi ^{2}\right) \ell _{k}\left( \xi ^{3}\right) . \end{aligned}$$

(2.49)

In the following, polynomial approximations are highlighted by capital letters, e.g. ${\mathbf {U}}$ is an approximation for the state vector $\mathbf{u}$ and $\mathbf{F} _{l}$, $l=1,2,3$, are approximations for the fluxes $\mathbf{f} _{l}$, $l=1,2,3$. The determinant J of the Jacobian matrix $\vec {\nabla }_{\vec {\xi }}\vec {\chi }$ is also approximated by tensor product Lagrange polynomials

$$\begin{aligned} J\left( \xi ^{1},\xi ^{2},\xi ^{3},t\right) \approx \mathrm {J}\left( \xi ^{1},\xi ^{2},\xi ^{3},t\right) :=\sum _{i,j,k=0}^{N}\mathrm {J}_{ijk}\left( t\right) \ell _{i}\left( \xi ^{1}\right) \ell _{j}\left( \xi ^{2}\right) \ell _{k}\left( \xi ^{3}\right) . \end{aligned}$$

(2.50)

In particular, the interpolation operator for a function ${\mathbf {g}}$ is given by

$$\begin{aligned} {\mathbb {I}}^{N}\!\left( {\mathbf {g}}\right) \left( \xi ^{1},\xi ^{2},\xi ^{3}\right) =\sum _{i,j,k=0}^{N}{\mathbf {g}}_{ijk}\ell _{i}\left( \xi ^{1}\right) \ell _{j}\left( \xi ^{2}\right) \ell _{k}\left( \xi ^{3}\right) , \end{aligned}$$

(2.51)

where ${\mathbf {g}}_{ijk}:={\mathbf {g}}\left( \xi _{i}^{1},\xi _{j}^{2},\xi _{k}^{3}\right)$ and $\left\{ \xi _{i}^{1}\right\} _{i=0}^{N}$, $\left\{ \xi _{i}^{2}\right\} _{i=0}^{N}$, $\left\{ \xi _{i}^{3}\right\} _{i=0}^{N}$ are sets of LGL points. Derivatives are approximated by exact differentiation of the polynomial interpolants. In general we have $\left( {\mathbb {I}}^{N}\!\left( g\right) \right) '\ne {\mathbb {I}}^{N-1}\!\left( g'\right)$ (cf. e.g. [7, 36]), as differentiation and interpolation only commute if there are no discretization errors. However, the contravariant coordinate vectors need to be discretized in such a way that the metric identities (2.20) are satisfied on the discrete level, too. Kopriva [35] introduced the conservative curl form that computes

$$\begin{aligned} {\mathbb {J}}a_{\beta }^{\alpha }:=-{\hat{x}}_{\alpha }\cdot \vec {\nabla }_{\xi }\times \left( {\mathbb {I}}^{N}\!\left( \chi _{\gamma }\vec {\nabla }_{\xi }\chi _{\delta }\right) \right) ,\quad \alpha =1,2,3,\quad \beta =1,2,3,\quad \left( \beta ,\gamma ,\delta \right) \ \text {cyclic},\nonumber \\ \end{aligned}$$

(2.52)

to approximate the metric terms. Here $\vec {\chi }=\left[ \chi _{1},\chi _{2},\chi _{3}\right] ^{T}$ represents the mapping from the element to the reference element and ${\hat{x}}_{i}$ is the unit vector in the i-th Cartesian coordinate direction. The representation (2.52) ensures that

$$\begin{aligned} \sum _{\alpha =1}^{3}\frac{\partial {\mathbb {I}}^{N}\!\left( {\mathbb {J}}a_{\beta }^{\alpha }\right) }{\partial \xi ^{\alpha }}=0,\quad \beta =1,2,3. \end{aligned}$$

(2.53)

From now on, the discrete contravariant coordinate vectors are denoted by ${\mathbb {J}}a_{\beta }^{\alpha }$, when the curl form (2.52) has been used to compute these quantities.

Integrals are approximated by a tensor product extension of a $2N-1$ accurate LGL quadrature formula. Hence, interpolation and quadrature nodes are collocated. In one spatial dimension the LGL quadrature formula is given by

$$\begin{aligned} \int \limits _{-1}^{1}g\left( \xi \right) \,d\xi \approx \sum _{i=0}^{N}\omega _{i}g\left( \xi _{i}\right) =\sum _{i=0}^{N}\omega _{i}g_{i}, \end{aligned}$$

(2.54)

where $\omega _{i}$, $i=0,\dots ,N$, are the quadrature weights and $\xi _{i}$, $i=0,\dots ,N$, are the LGL quadrature points. The formula (2.54) motivates the definition of the discrete quantity

$$\begin{aligned} \left\langle {\mathbf {f}},{\mathbf {g}}\right\rangle _{N}:=\sum _{i=0}^{N}\sum _{j=0}^{N}\sum _{k=0}^{N}\omega _{i}\omega _{j}\omega _{k}{\mathbf {f}}_{ijk}^{T}{\mathbf {g}}_{ijk}=\sum _{i,j,k=0}^{N}\omega _{ijk}{\mathbf {f}}_{ijk}^{T}{\mathbf {g}}_{ijk} \end{aligned}$$

(2.55)

for two functions ${\mathbf {f}}$ and ${\mathbf {g}}$. We note that (2.55) satisfies

$$\begin{aligned} \left\langle {\mathbb {I}}^{N}\!\left( {\mathbf {g}}\right) ,\varvec{\varphi }\right\rangle _{N}=\left\langle {\mathbf {g}},\varvec{\varphi }\right\rangle _{N}, \quad \forall \varvec{\varphi }\in {\mathbb {P}}^{N}\left( E,{\mathbb {R}}^{p}\right) . \end{aligned}$$

(2.56)

Furthermore, for a block vector ${\overset{\leftrightarrow }{\mathbf{f }}}$ and test functions $\varvec{\varphi }\in {\mathbb {P}}^{N}\left( E,{\mathbb {R}}^{p}\right)$, we define the discrete surface integral

$$\begin{aligned} \begin{aligned} \int \limits _{\partial E,N}\varvec{\varphi }^T\left\{ {\overset{\leftrightarrow }{\mathbf{f }}}\cdot {\hat{n}}\right\} \,dS&:= \sum _{j,k=0}^{N}\omega _{j}\omega _{k}\left( \varvec{\varphi }_{Njk}^{T}\left( {\mathbf {F}}_{1}\right) _{Njk}-\varvec{\varphi }_{0jk}^{T}\left( {\mathbf {F}}_{1}\right) _{0jk}\right) \\&\quad +\,\sum _{i,k=0}^{N}\omega _{i}\omega _{k}\left( \varvec{\varphi }_{iNk}^{T}\left( {\mathbf {F}}_{2}\right) _{iNk}-\varvec{\varphi }_{i0k}^{T}\left( {\mathbf {F}}_{2}\right) _{i0k}\right) \\&\quad +\sum _{i,j=0}^{N}\omega _{i}\omega _{j}\left( \varvec{\varphi }_{ijN}^{T}\left( {\mathbf {F}}_{3}\right) _{ijN}-\varvec{\varphi }_{ij0}^{T}\left( {\mathbf {F}}_{3}\right) _{ij0}\right) , \end{aligned} \end{aligned}$$

(2.57)

where ${\hat{n}}$ is the unit outward normal at the faces of the reference element E.

The spectral element approximation with LGL points for interpolation and quadrature provides a SBP operator $\mathcal {\mathcal {Q}}=\mathcal {\mathcal {M}}\,\mathcal {\mathcal {D}}$ with the mass matrix $\mathcal {\mathcal {M}}$ and the derivative matrix $\mathcal {\mathcal {D}}$. The mass matrix and the derivative matrix are given by

$$\begin{aligned} {\mathcal {M}}_{ij}=\omega _{i}\delta _{ij}, \quad {\mathcal {D}}_{ij}=\ell _{j}'\left( \xi _{i}\right) \quad i,j=0,\dots ,N. \end{aligned}$$

(2.58)

The important characteristic of this SBP operator is the property

$$\begin{aligned} \mathcal {\mathcal {Q}}+\mathcal {\mathcal {Q}}^T=\mathcal {\mathcal {B}}, \end{aligned}$$

(2.59)

where $\mathcal {\mathcal {B}}=\text {diag}\left( -1,0,\dots ,0,1\right)$. A SBP operator provides a discrete analogue of the integration-by-parts formula [19, 22, 38].

Finally, we note that in the LGL points $\xi _{i}^{1}$, $\xi _{j}^{2}$, $\xi _{k}^{3}$, $i,j,k=0,\dots ,N$, the Eq. (2.53) gives

$$\begin{aligned} \sum _{m=0}^{N}\left( {\mathcal {D}}_{im}\left( {\mathbb {J}}a_{\beta }^{1}\right) _{mjk}+{\mathcal {D}}_{jm}\left( {\mathbb {J}}a_{\beta }^{2}\right) _{imk}+{\mathcal {D}}_{km}\left( {\mathbb {J}}a_{\beta }^{3}\right) _{ijm}\right) =0,\quad \beta =1,2,3. \end{aligned}$$

(2.60)

2.5 The Semi-discrete Discontinuous Galerkin Method

Now, we apply the notation introduced in Sect. 2.4 and construct a moving mesh DGSEM. We discretize the Eqs. (2.30) and (2.33) simultaneously. In this way, it is ensured that the Eq. (2.30) is satisfied on the discrete level [37, 48, 64]. First, we replace the solution $\mathbf{u}$ by (2.49), the Jacobian J by (2.50) and approximate the fluxes by the interpolation operator (2.51). Next, we multiply the GCL (2.30) by test functions $\varphi \in {\mathbb {P}}^{N}\left( E\right)$, the Eq. (2.33) with $\varvec{\varphi }\in {\mathbb {P}}^{N}\left( E,{\mathbb {R}}^{p}\right)$, integrate the resulting equations and use integration-by-parts to separate boundary and volume contributions. The volume integrals in the variational form are approximated with the LGL quadrature. Then, we insert numerical surface fluxes $\vec {{\tilde{\nu }}}^{*}$ and $\overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}{}^{*}$ at the spatial element interfaces. Afterwards, we use the SBP property (2.59) for the volume contribution to get the standard DGSEM in strong form:

$$\begin{aligned} \left\langle \frac{\partial \mathrm {J}}{\partial \tau },\varphi \right\rangle _{N}&= \left\langle \vec {\nabla }_{\xi }\cdot {\mathbb {I}}^{N}\!\left( \vec {{\tilde{\nu }}}\right) ,\varphi \right\rangle _{N}+\int \limits _{\partial E,N}\varphi \left( {\tilde{\nu }}_{{\hat{n}}}^{*}-{\tilde{\nu }}_{{\hat{n}}}\right) \,dS, \quad \forall \varphi \in {\mathbb {P}}^{N}\left( E\right) , \end{aligned}$$

(2.61a)

$$\begin{aligned} \left\langle \frac{\partial \left( \mathrm {J}{\mathbf {U}}\right) }{\partial \tau },\varvec{\varphi }\right\rangle _{N}&= -\left\langle \vec {\nabla }_{\xi }\cdot {\mathbb {I}}^{N}\!\left( \overset{\leftrightarrow }{\tilde{{\mathbf {g}}}}\right) ,\varvec{\varphi }\right\rangle _{N}-\int \limits _{\partial E,N}\varvec{\varphi }^{T}\left( \tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}-\tilde{{\mathbf {G}}}_{{\hat{n}}}\right) \,dS, \quad \forall \varvec{\varphi }\in {\mathbb {P}}^{N}\left( E,{\mathbb {R}}^{p}\right) , \end{aligned}$$

(2.61b)

where we used the notation (2.55) and the notation (2.57) for the discrete surface integral.

The approximation of $\vec {{\tilde{\nu }}}$ and the nonlinear flux $\overset{\leftrightarrow }{\tilde{{\mathbf {g}}}}$ by the interpolation operator (2.51) causes aliasing errors in the standard strong form. The aliasing errors cannot be bounded and the errors are independent of the choice of the numerical surface flux. In Gassner [22] a detailed explanation and analysis of the aliasing problem is given. Furthermore, a specific reformulation of the volume integrals by using the skew-symmetry strategy has been developed to fix the aliasing problem. This approach has been enhanced and generalized by Gassner et al. in [23, 24] with a technique developed for high-order FD schemes (LeFloch et al. [40] or Fisher and Carpenter [20]). The generalized approach is called split form DG framework. Here, we proceed similar as in [24] and replace the interpolation operators in the discrete volume integrals by derivative projection operators. The interpolation operator in the discrete equation for the GCL (2.30) is replaced by

$$\begin{aligned} \begin{aligned} \vec {{\mathbb {D}}}^{N}\!\cdot \vec {{\tilde{\nu }}}_{ijk}&:= \sum _{m=0}^{N}\quad \,2\, {\mathcal {D}}_{im}\{\!\{\vec {\nu }\}\!\} _{\left( i,m\right) jk}\cdot \{\!\{{\mathbb {J}} \vec {a}^{1}\}\!\} _{\left( i,m\right) jk} \\&\quad +\,2\,{\mathcal {D}}_{jm}\{\!\{\vec {\nu }\}\!\} _{i\left( j,m\right) k}\cdot \{\!\{{\mathbb {J}}\vec {a}^{2}\}\!\} _{i\left( j,m\right) k} \\&\quad +\,2\,{\mathcal {D}}_{km}\{\!\{\vec {\nu }\}\!\} _{ij\left( k,m\right) }\cdot \{\!\{{\mathbb {J}}\vec {a}^{3}\}\!\} _{ij\left( k,m\right) } \end{aligned} \end{aligned}$$

(2.62)

with the volume averages of the metric terms, e.g.

$$\begin{aligned} \{\!\{\cdot \}\!\} _{(i,m)jk}:=\frac{1}{2}\left[ \left( \cdot \right) _{ ijk}+\left( \cdot \right) _{ mjk}\right] . \end{aligned}$$

(2.63)

The derivative projection operator in the discrete equation for (2.33) is computed as in [24]. Thus, the operator is given by

$$\begin{aligned} \begin{aligned} \vec {{\mathbb {D}}}^{N}\!\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}{}_{ijk}^{\text {EC}}&:= \sum _{m=0}^{N}\quad \,2\,{\mathcal {D}}_{im}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{mjk} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{1}\}\!\} _{\left( i,m\right) jk}\right) \\&\quad +2\,{\mathcal {D}}_{jm}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{imk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{imk} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{2}\}\!\} _{i\left( j,m\right) k}\right) \\&\quad +2\,{\mathcal {D}}_{km}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{ijm},{\mathbf {U}}_{ijk},{\mathbf {U}}_{ijm} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{3}\}\!\} _{ij\left( k,m\right) }\right) . \end{aligned} \end{aligned}$$

(2.64)

We note that the discrete volume weighted contravariant vectors ${\mathbb {J}}\vec {a}^{l}$, $l=1,2,3$, in the derivative projection operator (2.62) and (2.64) are computed by the conservative curl form (2.52). The flux $\overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}}$ is consistent and symmetric such that, e.g.

$$\begin{aligned} \begin{aligned} \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}}\left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}},{\mathbf {U}}\right) =\overset{\leftrightarrow }{{\mathbf {F}}}\left( {\mathbf {U}}\right) -\{\!\{\vec {v}\}\!\} _{\left( i,m\right) jk}{\mathbf {U}}, \end{aligned} \end{aligned}$$

(2.65)

and

$$\begin{aligned} \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}}\left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{mjk}\right) =\overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}}\left( \vec {\nu }_{mjk},\vec {\nu }_{ijk},{\mathbf {U}}_{mjk},{\mathbf {U}}_{ijk}\right) , \end{aligned}$$

(2.66)

for $i,j,k,m=0,\dots ,N$. Furthermore, the flux functions ${\mathbf {G}}_{l}^{\text {EC}}$, $l=1,2,3$, satisfy for $i,j,k,m=0,\dots ,N$, the following discrete entropy conditions

$$\begin{aligned} \begin{aligned}&[\![{\mathbf {W}}]\!] _{(i,m)jk}^{T}{\mathbf {G}}_{l}^{\text {EC}}\left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{mjk}\right) =[\![\Psi _{l}]\!] _{(i,m)jk}-\{\!\{\nu _{l}\}\!\} _{\left( i,m\right) jk}[\![\Phi ]\!] _{(i,m)jk}, \\&[\![{\mathbf {W}}]\!] _{i(j,m)k}^{T}{\mathbf {G}}_{l}^{\text {EC}}\left( \vec {\nu }_{ijk},\vec {\nu }_{imk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{imk}\right) =[\![\Psi _{l}]\!] _{i(j,m)k}-\{\!\{\nu _{l}\}\!\} _{i\left( j,m\right) k}[\![\Phi ]\!] _{i(j,m)k}, \\&[\![{\mathbf {W}}]\!] _{ij(k,m)}^{T}{\mathbf {G}}_{l}^{\text {EC}}\left( \vec {\nu }_{ijk},\vec {\nu }_{ijm},{\mathbf {U}}_{ijk},{\mathbf {U}}_{ijm}\right) =[\![\Psi _{l}]\!] _{ij(k,m)}-\{\!\{\nu _{l}\}\!\} _{ij\left( k,m\right) }[\![\Phi ]\!] _{ij(k,m)}. \end{aligned} \end{aligned}$$

(2.67)

The quantities $\Phi$ and $\Psi _{l}$ are polynomial approximations which satisfy in the LGL points

$$\begin{aligned} \Phi _{ijk}={\mathbf {W}}_{ijk}^{T}{\mathbf {U}}_{ijk}-S_{ijk}, \quad \left( \Psi _{l}\right) _{ijk}:={\mathbf {W}}_{ijk}^{T}\left( {\mathbf {F}}_{l}\right) _{ijk}-\left( F_{l}^{s}\right) _{ijk}, \quad l=1,2,3, \end{aligned}$$

(2.68)

where ${\mathbf {W}}_{ijk}$, $S_{ijk}$ and $\left( F_{l}^{s}\right) _{ijk}$ are the nodal values of the polynomials

$$\begin{aligned} {\mathbf {W}}:={\mathbb {I}}^{N}\!\left( {\mathbf {w}}\right) , \quad S:={\mathbb {I}}^{N}\!\left( s\right) , \quad F_{l}^{s}:={\mathbb {I}}^{N}\!\left( f_{l}^{s}\right) , \quad l=1,2,3. \end{aligned}$$

(2.69)

Here, s represents an entropy for the system (2.1) with the corresponding entropy flux functions $f_{l}^{s}$, $l=1,2,3$, and entropy variables $\mathbf{w}$. Furthermore, the volume jumps in (2.67) are, e.g.

$$\begin{aligned}{}[\![\cdot ]\!] _{(i,m)jk}:=\left( \cdot \right) _{ijk}-\left( \cdot \right) _{mjk}. \end{aligned}$$

(2.70)

In Appendix B, flux functions with these properties are presented for the Euler equations.

Finally, for each element $e_{\kappa }(t)$ the semi-discrete moving mesh DGSEM can be written in the following form:

$$\begin{aligned} \left\langle \frac{\partial \mathrm {J}}{\partial \tau },\varphi \right\rangle _{N}&= \left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \vec {{\tilde{\nu }}},\varphi \right\rangle _{N}+\int \limits _{\partial E,N}\varphi \left( {\tilde{\nu }}_{{\hat{n}}}^{*}-{\tilde{\nu }}_{{\hat{n}}}\right) \,dS, \quad \forall \varphi \in {\mathbb {P}}^{N}\left( E\right) , \end{aligned}$$

(2.71a)

$$\begin{aligned} \left\langle \frac{\partial \left( \mathrm {J}{\mathbf {U}}\right) }{\partial \tau },\varvec{\varphi }\right\rangle _{N}&= -\left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}{}^{\text {EC}},\varvec{\varphi }\right\rangle _{N}-\int \limits _{\partial E,N}\varvec{\varphi }^{T}\left( \tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}-\tilde{{\mathbf {G}}}_{{\hat{n}}}\right) \,dS, \quad \forall \varvec{\varphi }\in {\mathbb {P}}^{N}\left( E,{\mathbb {R}}^{p}\right) . \end{aligned}$$

(2.71b)

The unit outward facing normal vector and surface element on the element side are constructed from the element metrics by

$$\begin{aligned} \vec {n}:=\frac{1}{{\hat{s}}}\sum _{l=1}^{3}\left( {\mathbb {J}}\vec {a}^{l}\right) {\hat{n}}^{l},\quad {\hat{s}}:=\left| \sum _{l=1}^{3}\left( {\mathbb {J}}\vec {a}^{l}\right) {\hat{n}}^{l}\right| . \end{aligned}$$

(2.72)

Thus, the quantity ${\tilde{\nu }}_{{\hat{n}}}$ in (2.71a) and the flux $\tilde{{\mathbf {G}}}_{{\hat{n}}}$ in (2.71b) are defined by

$$\begin{aligned} {\tilde{\nu }}_{{\hat{n}}}&= \left( {\hat{s}}\vec {n}\right) \cdot \vec {\nu }=\sum _{l=1}^{3}{\hat{n}}^{l}\left( {\mathbb {J}}a_{1}^{l}\nu _{1}+{\mathbb {J}}a_{2}^{l}\nu _{2}+{\mathbb {J}}a_{3}^{l}\nu _{3}\right) , \end{aligned}$$

(2.73)

$$\begin{aligned} \tilde{{\mathbf {G}}}_{{\hat{n}}}&= \left( {\hat{s}}\vec {n}\right) \cdot \overset{\leftrightarrow }{{\mathbf {G}}}=\sum _{l=1}^{3}{\hat{n}}^{l}\left( {\mathbb {J}}a_{1}^{l}{\mathbf {G}}_{1}+{\mathbb {J}}a_{2}^{l}{\mathbf {G}}_{2}+{\mathbb {J}}a_{3}^{l}{\mathbf {G}}_{3}\right) =\left\{ \varvec{\mathcal {M}}\,\overset{\leftrightarrow }{{\mathbf {G}}}\right\} \cdot {\hat{n}}. \end{aligned}$$

(2.74)

To define the numerical surface fluxes in (2.71a) and (2.71b), we introduce notation for states at the LGL nodes along an interface between two spatial elements to be a primary “−” and complement the notation with a secondary “$+$” to denote the value at the LGL nodes on the opposite side. Then the orientated jump and the arithmetic mean at the interfaces are defined by

$$\begin{aligned}{}[\![\cdot ]\!] :=\left( \cdot \right) ^{+}-\left( \cdot \right) ^{-}, \quad \text {and} \quad \{\!\{\cdot \}\!\} :=\frac{1}{2}\left[ \left( \cdot \right) ^{+}+\left( \cdot \right) ^{-}\right] . \end{aligned}$$

(2.75)

When applied to vectors, the average and jump operators are evaluated separately for each vector component. Then the normal vector $\vec {n}$ is defined unique to point from the “−” to the “$+$” side. This notation allows to compute the contravariant surface numerical fluxes in (2.71a) as

$$\begin{aligned} {\tilde{\nu }}_{{\hat{n}}}^{*}={\hat{s}}\left( n_{1}\{\!\{v_{1}\}\!\} +n_{2}\{\!\{v_{2}\}\!\} +n_{3}\{\!\{v_{3}\}\!\} \right) . \end{aligned}$$

(2.76)

We note that due to the assumptions made in Sect. 2.1, the mesh velocity is a continuous function and the averages reduce to the uniquely defined values on the surface. The contravariant surface numerical fluxes in (2.71b) are given by

$$\begin{aligned} \tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}={\hat{s}}\left( n_{1}{\mathbf {G}}_{1}^{\text {EC}}+n_{2}{\mathbf {G}}_{2}^{\text {EC}}+n_{3}{\mathbf {G}}_{3}^{\text {EC}}\right) , \end{aligned}$$

(2.77)

where the Cartesian fluxes ${\mathbf {G}}_{l}^{\text {EC}}$, $l=1,2,3$, satisfy (2.65), (2.66), (2.67). We note that these fluxes are the baseline choices without interface dissipation, to get a baseline scheme that is entropy conservative.

Remark 2.3

• (i) The discrete volume weighted contravariant vectors ${\mathbb {J}}\vec {a}^{\alpha }$, $\alpha =1,2,3$, do not dependent on the solution $\mathrm {J}$ of (2.71a), since these vectors are computed by the conservative curl form (2.52). Thus, the discrete metric identities (2.53) are satisfied and the normal computation (2.72) is watertight. This means the normal vector and the surface element are continuous across element interfaces.

• (ii) Since the discrete volume weighted contravariant vectors ${\mathbb {J}}\vec {a}^{\alpha }$, $\alpha =1,2,3$, are computed by the conservative curl form (2.52), the Eq. (2.20) is satisfied on the discrete level.

• (iii) The Eqs. (2.71a) and (2.71a) ensure that the Eq. (2.30) is satisfied on the discrete level.

2.6 Semi-discrete Entropy Conservation

The spatial integral of the entropy is bounded in time on the continuous level. Thus, it is desirable that a numerical method is stable in the sense that a discrete version of this integral is bounded in time, too. In the context of the moving mesh semi-discrete DGSEM (2.71), we are interested to find an upper bound for the quantity

$$\begin{aligned} {\bar{S}}\left( \tau \right) :=\sum _{k=1}^{K}\left\langle S\left( \tau \right) ,\mathrm {J}\left( \tau \right) \right\rangle _{N},\quad \forall \tau \in \left[ 0,T\right] , \end{aligned}$$

(2.78)

where $S={\mathbb {I}}^{N}\!\left( s\right)$ is a polynomial approximation for the entropy s. Next, we prove the following statement for the semi-discrete moving mesh DGSEM.

Theorem 2.4

Suppose the flux functions $\overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}}$ in the derivative projection operator (2.64), the numerical surface fluxes $\tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}$ are computed by Cartesian fluxes ${\mathbf {G}}_{l}^{\text {EC}}$, $l=1,2,3$, with the properties (2.65), (2.66), (2.67) and periodic boundary conditions are used. Then the semi-discrete moving mesh DGSEM (2.71) satisfies the discrete entropy equation

$$\begin{aligned} {\bar{S}}\left( \tau \right) ={\bar{S}}\left( 0\right) , \quad \forall \tau \in \left[ 0,T\right] , \end{aligned}$$

(2.79)

where ${\bar{S}}\left( \tau \right)$ is given by (2.78).

Proof

We proceed similar as in the continuous entropy analysis, use the polynomial approximation $\varvec{\varphi }={\mathbb {I}}^{N}\!\left( {\mathbf {w}}\right) ={\mathbf {W}}$ as test function in the Eq. (2.71b) and obtain

$$\begin{aligned} \left\langle \frac{\partial \left( \mathrm {J}{\mathbf {U}}\right) }{\partial \tau },{\mathbf {W}}\right\rangle _{N}=-\left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}{}^{\text {EC}},{\mathbf {W}}\right\rangle _{N}-\int \limits _{\partial E,N}{\mathbf {W}}^{T}\left( \tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}-\tilde{{\mathbf {G}}}_{{\hat{n}}}\right) \,dS. \end{aligned}$$

(2.80)

First, we consider the left hand side in the Eq. (2.80). Since interpolation and quadrature nodes are collocated, the nodal values can be analyzed by the same arguments as in the continuous computations (2.38) and (2.39). Hence, we obtain for all $i,j,k=0,\dots ,N$

$$\begin{aligned} \begin{aligned} \mathrm {J}_{ijk}{\mathbf {W}}_{ijk}^{T}\left( \frac{\partial }{\partial \tau }{\mathbf {U}}_{ijk}\right)&=\mathrm {J}_{ijk}{\mathbf {W}}_{ijk}^{T}\frac{\partial {\mathbf {U}}_{ijk}}{\partial t}+{\mathbf {W}}_{ijk}^{T}\left( \vec {{\tilde{\nu }}}_{ijk}\cdot \vec {\nabla }_{\xi }{\mathbf {U}}_{ijk}\right) \\&=\mathrm {J}_{ijk}\frac{\partial S_{ijk}}{\partial t}+\vec {{\tilde{\nu }}}\cdot \vec {\nabla }_{\xi }S_{ijk}=J_{ijk}\left( \frac{\partial }{\partial \tau }S_{ijk}\right) . \end{aligned} \end{aligned}$$

(2.81)

Next we multiply the Eq. (2.81) by $\omega _{ijk}$ and compute the sum over all LGL nodes. This gives

$$\begin{aligned} \left\langle \mathrm {J}\frac{\partial {\mathbf {U}}}{\partial \tau },{\mathbf {W}}\right\rangle _{N}=\left\langle \frac{\partial S}{\partial \tau },\mathrm {J}\right\rangle _{N}. \end{aligned}$$

(2.82)

Since we assume time continuity for our semi-discrete analysis, we apply the product rule in time and obtain by (2.82)

$$\begin{aligned} \begin{aligned} \left\langle \frac{\partial \left( \mathrm {J}{\mathbf {U}}\right) }{\partial \tau },{\mathbf {W}}\right\rangle _{N}&= \left\langle \frac{\partial S}{\partial \tau },\mathrm {J}\right\rangle _{N}+\left\langle \frac{\partial J}{\partial \tau },{\mathbf {W}}^{T}{\mathbf {U}}\right\rangle _{N} \\&= \frac{\partial }{\partial \tau }\left\langle S,J\right\rangle _{N}+\left\langle \frac{\partial \mathrm {J}}{\partial \tau },\Phi \right\rangle _{N} \\&= \frac{\partial }{\partial \tau }\left\langle S,J\right\rangle _{N}+\left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \vec {{\tilde{\nu }}},\Phi \right\rangle _{N}+\int \limits _{\partial E,N}\left( {\tilde{\nu }}_{{\hat{n}}}^{*}-{\tilde{\nu }}_{{\hat{n}}}\right) \Phi \,dS, \end{aligned} \end{aligned}$$

(2.83)

where we used in the last step the Eq. (2.71a) with the test function $\varphi =\Phi$. We note that the quantity $\Phi$ is defined as a polynomial with the nodal values (2.68). In the Appendix C.1, the following equation is proven

$$\begin{aligned} \left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}{}^{\text {EC}},{\mathbf {W}}\right\rangle _{N}=\int \limits _{\partial E,N}\left( \tilde{F}_{{\hat{n}}}^{s}-{\tilde{\nu }}_{{\hat{n}}}S\right) \,dS-\left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \vec {{\tilde{\nu }}},\Phi \right\rangle _{N}, \end{aligned}$$

(2.84)

where $\tilde{F}_{{\hat{n}}}^{s}=\left( {\hat{s}}\vec {n}\right) \cdot \vec {F}^{s}$ with $\vec {F}^{s}=\left[ F_{1}^{s},F_{2}^{s},F_{3}^{s}\right] ^{T}$. Here the polynomials $F_{l}^{s}$, $l=1,2,3$, are given by (2.69). Moreover, we obtain by (2.73) and (2.74)

$$\begin{aligned} \begin{aligned}&-{\mathbf {W}}^{T}\left( \tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}- \tilde{{\mathbf {G}}}_{{\hat{n}}}\right) -\left( \tilde{F}_{{\hat{n}}}^{s}- {\tilde{\nu }}_{{\hat{n}}}S\right) \\&\quad =\sum _{l=1}^{3}\left\{ {\hat{s}}n_{l}\left( {\mathbf {W}}^{T}{\mathbf {F}}_{l}-F_{l}^{s}\right) -{\hat{s}}n_{l}\left( {\mathbf {W}}^{T}{\mathbf {U}}-S\right) \right\} -{\mathbf {W}}^{T}\tilde{{\mathbf {G}}}_{{\hat{n}}}^{*} \\&\quad ={\tilde{\Psi }}_{{\hat{n}}}-{\tilde{\nu }}_{{\hat{n}}}\Phi - {\mathbf {W}}^{T}\tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}, \end{aligned} \end{aligned}$$

(2.85)

where $\Phi$ as well as $\Psi _{l}$, $l=1,2,3$, are polynomials with nodal values (2.68) and ${\tilde{\Psi }}_{{\hat{n}}}:=\left( {\hat{s}}\vec {n}\right) \cdot \vec {\Psi }$ with $\vec {\Psi }=\left[ \Psi _{1},\Psi _{2},\Psi _{3}\right] ^{T}$. Next, we plug the Eqs. (2.83), (2.84), (2.85) in (2.80) and rearrange. This results in the equation

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial \tau }\left\langle S,J\right\rangle _{N}&= -\int \limits _{\partial E,N}\left\{ {\mathbf {W}}^{T}\left( \tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}- \tilde{{\mathbf {G}}}_{{\hat{n}}}\right) +\left( \tilde{F}_{{\hat{n}}}^{s} -{\tilde{\nu }}_{{\hat{n}}}S\right) -\left( {\tilde{\nu }}_{{\hat{n}}}^{*} -{\tilde{\nu }}_{{\hat{n}}}\right) \Phi \right\} \,dS \\&= \int \limits _{\partial E,N}\left( {\tilde{\Psi }}_{{\hat{n}}}-{\tilde{\nu }}_{{\hat{n}}}^{*} \Phi -{\mathbf {W}}^{T}\tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}\right) \,dS. \end{aligned} \end{aligned}$$

(2.86)

Then, we sum the Eq. (2.86) over all elements and use that the normal computation (2.72) is watertight. This provides the equation

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial \tau }{\bar{S}}\left( \tau \right)&= \quad \underset{\text {faces}}{\sum _{\text {Boundary}}}\ \int \limits _{\partial E,N}\left( {\tilde{\Psi }}_{{\hat{n}}}-{\nu }_{{\hat{n}}}^{*} \Phi \tilde{-}{\mathbf {W}}^{T}\tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}\right) \,dS \\&\quad -\underset{\text {faces}}{\sum _{\text {Interior}}}\int \limits _{\partial E,N} \left( [\![{\tilde{\Psi }}_{{\hat{n}}}]\!] -\{\!\{{\tilde{\nu }}_{{\hat{n}}}\}\!\} [\![\Phi ]\!] -[\![{\mathbf {W}}]\!] ^{T}\tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}\right) \,dS. \end{aligned} \end{aligned}$$

(2.87)

Since the numerical surface fluxes $\tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}$ are computed by Cartesian fluxes ${\mathbf {G}}_{l}^{\text {EC}}$, $l=1,2,3$, with the properties (2.67), it follows

$$\begin{aligned}{}[\![{\tilde{\Psi }}_{{\hat{n}}}]\!] -\{\!\{{\tilde{\nu }}_{{\hat{n}}}\}\!\} [\![\Phi ]\!] -[\![{\mathbf {W}}]\!] ^{T}\tilde{{\mathbf {G}}}_{{\hat{n}}}^{*} =\sum _{l=1}^{3}{\hat{s}}n_{l}\left( [\![\Psi _{l}]\!] -\{\!\{\nu _{l}\}\!\} [\![\Phi ]\!] -[\![{\mathbf {W}}]\!] ^{T}{\mathbf {G}}_{l}^{*}\right) =0. \end{aligned}$$

(2.88)

Hence, we obtain the equation

$$\begin{aligned} \frac{\partial }{\partial \tau }{\bar{S}}\left( \tau \right) = \underset{\text {faces}}{\sum _{\text {Boundary}}}\ \int \limits _{\partial E,N} \left( {\tilde{\Psi }}_{{\hat{n}}}-{\tilde{\nu }}_{{\hat{n}}}^{*}\Phi -{\mathbf {W}}^{T}\tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}\right) \,dS. \end{aligned}$$

(2.89)

Since the method is investigated with periodic boundary conditions, we obtain the desired entropy equation by integrating the Eq. (2.89) over the time interval [0, T]. This completes the proof of Theorem 2.4. $\square$

Remark 2.5

The proof of Theorem 2.4 requires the assumptions that the time integration is exact and that properties like positivity preservation (of the water height, density or pressure) are satisfied on the discrete level.

For non-periodic boundary conditions, a proper choice of discrete boundary condition is necessary to bound the term

$$\begin{aligned} \underset{\text {faces}}{\sum _{\text {Boundary}}}\ \int \limits _{\partial E,N} \left( {\tilde{\Psi }}_{{\hat{n}}}-{\tilde{\nu }}_{{\hat{n}}}^{*}\Phi -{\mathbf {W}}^{T} \tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}\right) \,dS \end{aligned}$$

(2.90)

in Eq. (2.89) such that the method becomes entropy conservative/stable. Thus, we obtain from Theorem 2.4 the following Corollary.

Corollary 2.6

Suppose the flux functions $\overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}}$ in the derivative projection operator (2.64) and the numerical surface fluxes $\tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}$ (2.77) are computed by Cartesian fluxes ${\mathbf {G}}_{l}^{\text {EC}}$, $l=1,2,3$, with the properties (2.65), (2.66), (2.67) and a proper dissipative boundary condition, e.g., [14, 31, 53], is applied. Then the semi-discrete moving mesh DGSEM (2.71) satisfies the discrete entropy inequality

$$\begin{aligned} {\bar{S}}\left( \tau \right) \le {\bar{S}}\left( 0\right) , \quad \forall \tau \in \left[ 0,T\right] . \end{aligned}$$

(2.91)

2.7 Semi-discrete Entropy Stability

Entropy conservation can be merely expected when a reversible process is described by a system of PDEs. In general, conservation laws are describing irreversible processes with discontinuous solutions. Hence, it cannot be expected that the entropy conservative moving mesh DGSEM provides a physical meaningful discretization for the system (2.1). However, the entropy conservative flux at the element interfaces can be augmented by an artificial dissipation term.

In the literature, there are different strategies to add dissipation to an entropy conservative flux. Here, dissipation is added via a matrix operator. This approach, for instance, has been used in the context of gas dynamics by Chandrashekar [8] or Winters et al. [63].

The conservative variables $\mathbf{u}$ can be written in dependence of the entropy variables $\mathbf{w}$. Differentiation of the conservative variables $\mathbf{u} =\mathbf{u} (\mathbf{w} )$ provides the symmetric positive definite matrix $\frac{\partial \mathbf{u} }{\partial \mathbf{w} }$, since the system (2.1) is assumed to be symmetrizable (cf. e.g. [29]). Thus, it follows by a Taylor expansion up to first order

$$\begin{aligned}{}[\![\mathbf{u} ]\!] =\left( \frac{\partial \mathbf{u} }{\partial \mathbf{w} }\right) [\![\mathbf{w} ]\!] +{\mathcal {O}}\left( \left| [\![\mathbf{w} ]\!] \right| ^{2}\right) , \end{aligned}$$

(2.92)

where the jump operator is defined by (2.75) at the interfaces. Furthermore, the system (2.1) is hyperbolic. Thus, the flux Jacobian matrices $\frac{\partial \mathbf{f} _{l}}{\partial \mathbf{u} }$, $l=1,2,3$, are diagonalizable and have real eigenvalues $\left\{ \lambda _{i}^{l}\left( \mathbf{u} \right) \right\} _{i=1}^{p}\subseteq {\mathbb {R}}$. The corresponding right eigenvector matrices are $\mathcal {\mathcal {R}}_{l}$. For the Euler equations Merriam [47] has shown that there are block diagonal scaling matrices such that the Hessian matrix of the entropy can be represented by scaled right eigenvector matrices. This result has been generalized and is known as the eigenvector scaling theorem (cf. Barth [2, Theorem 4]). Hence, according to the eigenvector scaling theorem, there are symmetric block diagonal scaling matrices $\mathcal {\mathcal {T}}_{l}$ with

$$\begin{aligned} \frac{\partial {\mathbf {f}}_{l}}{\partial {\mathbf {u}}}=\tilde{\mathcal {\mathcal {R}}}_{l}\, \Lambda _{l}\left( {\mathbf {u}}\right) \,\tilde{\mathcal {\mathcal {R}}}_{l}^{-1}, \quad \frac{\partial {\mathbf {u}}}{\partial {\mathbf {w}}}=\tilde{\mathcal {\mathcal {R}}}_{l}\, \tilde{\mathcal {\mathcal {R}}}_{l}^{T},\quad \tilde{\mathcal {\mathcal {R}}}_{l}=\mathcal {\mathcal {R}}_{l}\, \mathcal {\mathcal {T}}_{l},\quad l=1,2,3, \end{aligned}$$

(2.93)

where $\Lambda _{l}\left( {\mathbf {u}}\right) :=\text {diag}\left( \lambda _{1}^{l}\left( {\mathbf {u}}\right) ,\dots ,\lambda _{p}^{l}\left( {\mathbf {u}}\right) \right)$. The flux Jacobian matrices $\frac{\partial \mathbf{g} _{l}}{\partial \mathbf{u} }=\frac{\partial \mathbf{f} _{l}}{\partial \mathbf{u} }-\nu _{l}\mathcal {\mathcal {I}}_{p}$ have the real eigenvalues $\left\{ \lambda _{i}^{l}\left( {\mathbf {u}}\right) -\nu _{l}\right\} _{i=1}^{p}$ and the same right eigenvectors as the flux Jacobian $\frac{\partial \mathbf{f} _{l}}{\partial \mathbf{u} }$. We note that $\mathcal {\mathcal {I}}_{p}$ is the $p\times p$ identity matrix. Hence, it follows

$$\begin{aligned}&\frac{\partial {\mathbf {g}}_{l}}{\partial {\mathbf {u}}}=\tilde{\mathcal {\mathcal {R}}_{l}}\, \Lambda _{l}\left( \nu ,{\mathbf {u}}\right) \,\tilde{\mathcal {\mathcal {R}}}_{l}^{-1}, \quad \Lambda _{l}\left( \nu ,{\mathbf {u}}\right) :=\text {diag}\left( \lambda _{1}^{l} \left( {\mathbf {u}}\right) -\nu _{l},\dots ,\lambda _{p}^{l}\left( {\mathbf {u}} \right) -\nu _{l}\right) ,\nonumber \\&\quad l=1,2,3. \end{aligned}$$

(2.94)

Furthermore, we obtain by (2.93)

$$\begin{aligned} \left( \frac{\partial {\mathbf {g}}_{l}}{\partial {\mathbf {w}}}\right) = \left( \frac{\partial {\mathbf {g}}_{l}}{\partial {\mathbf {u}}}\right) \left( \frac{\partial {\mathbf {u}}}{\partial {\mathbf {w}}}\right) =\tilde{\mathcal {\mathcal {R}}}_{l}\, \Lambda _{l}\left( \nu ,{\mathbf {u}}\right) \,\tilde{\mathcal {\mathcal {R}}}_{l}^{T},\quad l=1,2,3. \end{aligned}$$

(2.95)

The Eq. (2.95) motivates the definition of the following matrix dissipation operators

$$\begin{aligned} \mathcal {\mathcal {H}}_{l}=\hat{\mathcal {\mathcal {R}}}_{l}\,\left| \Lambda _{l}\right| \,\hat{\mathcal {\mathcal {R}}}_{l}^{T}, \quad \hat{\mathcal {\mathcal {R}}}_{l}=\mathcal {\mathcal {R}}_{l}^{\star }\mathcal {\mathcal {T}}_{l}^{\star } ,\quad l=1,2,3. \end{aligned}$$

(2.96)

where the matrices $\mathcal {\mathcal {R}}_{l}^{\star }$, $\mathcal {\mathcal {T}}_{l}^{\star }$, depend on some averaged values of the states ${\mathbf {U}}^{-}$, ${\mathbf {U}}^{+}$ and they are consistent with the right eigenvector matrix $\mathcal {\mathcal {R}}_{l}$ and the scaling matrix $\mathcal {\mathcal {T}}_{l}$. The matrix $\left| \Lambda _{l}\right|$ depends on the values $\left\{ \lambda _{i}^{l}\left( {\mathbf {U}}^{-}\right) -\nu _{l}^{-}\right\} _{i=1}^{p}$ and $\left\{ \lambda _{i}^{l}\left( {\mathbf {U}}^{+}\right) -\nu _{l}^{+}\right\} _{i=1}^{p}$. The matrix $\mathcal {\mathcal {H}}_{l}$ needs to be a symmetric positive definite matrix. Therefore, the matrix $\left| \Lambda _{l}\right|$ has to be chosen carefully. In Appendix B.3, the matrices to construct the dissipation operator (2.96) for the compressible Euler equations are given. There it can be also seen which average values are used to evaluate the states ${\mathbf {U}}^{-}$, ${\mathbf {U}}^{+}$ in the matrices.

The dissipation operator (2.96) is used to modify the Cartesian numerical surface flux at the element interfaces as follows

$$\begin{aligned} {\mathbf {G}}_{l}^{\text {ES}}:={\mathbf {G}}_{l}^{\text {EC}}-\frac{1}{2}\, \mathcal {\mathcal {H}}_{l}\,[\![{\mathbf {W}}]\!] , \quad l=1,2,3, \end{aligned}$$

(2.97)

where the Cartesian fluxes ${\mathbf {G}}_{l}^{\text {EC}}$, $l=1,2,3$, satisfy (2.65), (2.66), (2.67). The contravariant surface numerical fluxes $\tilde{{\mathbf {G}}}_{{\hat{n}}}^{\text {EC}}$ are computed by (2.77). We note that the dissipation operator (2.96) is not used to modify the entropy conservative fluxes in the derivative projection operator (2.64).

The numerical fluxes $\tilde{{\mathbf {G}}}_{{\hat{n}}}^{\text {ES}}$ do not provide an entropy conservative scheme, but the result in Theorem 2.4 can be used to prove that the moving mesh DGSEM becomes entropy stable, such that the discrete mathematical entropy is bounded at any time by its initial data, when the numerical fluxes $\tilde{{\mathbf {G}}}_{{\hat{n}}}^{\text {ES}}$ are used at the element interfaces and it is assumed that the time integration is exact and that properties like positivity preservation (of the water height, density or pressure) are satisfied on the discrete level.

Corollary 2.7

Suppose the flux functions $\overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}}$ in the derivative projection operator (2.64) are computed by Cartesian fluxes ${\mathbf {G}}_{l}^{\text {EC}}$, $l=1,2,3$, with the properties (2.65), (2.66), (2.67), the numerical surface fluxes $\tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}=\tilde{{\mathbf {G}}}_{{\hat{n}}}^{\text {ES}}$ are computed by the Cartesian fluxes ${\mathbf {G}}_{l}^{\text {ES}}$, $l=1,2,3$, given by (2.97) and periodic boundary conditions are used. Then the semi-discrete moving mesh DGSEM (2.71) satisfies the discrete entropy inequality

$$\begin{aligned} {\bar{S}}\left( \tau \right) \le {\bar{S}}\left( 0\right) , \quad \forall \tau \in \left[ 0,T\right] . \end{aligned}$$

(2.98)

Furthermore, with proper dissipative boundary conditions, the method satisfies again the inequality (2.98) for non-periodic problems.

Proof

We proceed as in the proof of Theorem 2.4 and obtain the equation

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial \tau }{\bar{S}}\left( \tau \right)&= \quad \underset{\text {faces}}{\sum _{\text {Boundary}}}\ \int \limits _{\partial E,N}\left( {\tilde{\Psi }}_{{\hat{n}}} -{\tilde{\nu }}_{{\hat{n}}}^{*}\Phi -{\mathbf {W}}^{T} \tilde{{\mathbf {G}}}_{{\hat{n}}}^{\text {ES}}\right) \,dS \\&\quad -\underset{\text {faces}}{\sum _{\text {Interior}}} \int \limits _{\partial E,N}\left( [\![{\tilde{\Psi }}_{{\hat{n}}}]\!] -\{\!\{{\tilde{\nu }}_{{\hat{n}}}\}\!\} [\![\Phi ]\!] -[\![{\mathbf {W}}]\!] ^{T} \tilde{{\mathbf {G}}}_{{\hat{n}}}^{\text {ES}}\right) \,dS. \end{aligned} \end{aligned}$$

(2.99)

Since the numerical surface fluxes $\tilde{{\mathbf {G}}}_{{\hat{n}}}^{\text {ES}}$ are computed by the Cartesian fluxes (2.97) and the fluxes ${\mathbf {G}}_{l}^{\text {EC}}$, $l=1,2,3$, satisfy (2.67), it follows

$$\begin{aligned} \begin{aligned}&[\![{\tilde{\Psi }}_{{\hat{n}}}]\!] -[\![\Phi ]\!] \{\!\{{\tilde{\nu }}_{{\hat{n}}}\}\!\} -[\![{\mathbf {W}}]\!] ^{T}\tilde{{\mathbf {G}}}_{{\hat{n}}}^{\text {ES}} \\&\quad =\sum _{l=1}^{3}{\hat{s}}n_{l}\left( [\![\Psi _{l}]\!] -[\![\Phi ]\!] \{\!\{\nu _{l}\}\!\} -[\![{\mathbf {W}}]\!] ^{T}{\mathbf {G}}_{l}^{\text {EC}}+\frac{1}{2} [\![{\mathbf {W}}]\!] ^{T}\mathcal {\mathcal {H}}_{l}[\![{\mathbf {W}}]\!] \right) \\&\quad =\frac{1}{2}\sum _{l=1}^{3}{\hat{s}}n_{l}[\![{\mathbf {W}}]\!] ^{T} \mathcal {\mathcal {H}}_{l}[\![{\mathbf {W}}]\!] . \end{aligned} \end{aligned}$$

(2.100)

Since the matrices $\mathcal {\mathcal {H}}_{l}$, $l=1,2,3$, are symmetric positive definite and the outward normal vectors of the curved elements are positive oriented, the Eq. (2.100) provides

$$\begin{aligned} -\underset{\text {faces}}{\sum _{\text {Interior}}}\int \limits _{\partial E,N} \left( [\![{\tilde{\Psi }}_{{\hat{n}}}]\!] -\{\!\{{\tilde{\nu }}_{{\hat{n}}}\}\!\} [\![\Phi ]\!] -[\![{\mathbf {W}}]\!] ^{T}\tilde{{\mathbf {G}}}_{{\hat{n}}}^{\text {ES}}\right) \,dS\le 0. \end{aligned}$$

(2.101)

Hence, we obtain the inequality

$$\begin{aligned} \frac{\partial }{\partial \tau }{\bar{S}}\left( \tau \right) \le \underset{\text {faces}}{\sum _{\text {Boundary}}}\ \int \limits _{\partial E,N}\left( {\tilde{\Psi }}_{{\hat{n}}}-{\tilde{\nu }}_{{\hat{n}}}^{*} \Phi -{\mathbf {W}}^{T}\tilde{{\mathbf {G}}}_{{\hat{n}}}^{\text {ES}}\right) \,dS. \end{aligned}$$

(2.102)

The right hand side of the inequality vanishes, since the method is investigated with periodic boundary conditions. Hence, we obtain the the desired inequality (2.98) by integrating (2.102) over the temporal interval $\left[ 0,T\right]$. $\square$

2.8 Free Stream Preservation for the Moving Mesh DGSEM

In this section, we check the discretization of the geometric and metric terms in time. Since DG methods with the forward Euler discretization are unstable [9, 16], we investigate directly the discretization by an explicit RK method with $s\ge 2$ stages and the characteristic coefficients $\left\{ a_{\varrho \sigma }\right\} _{\varrho ,\sigma =1}^{s}$, $\left\{ b_{\sigma }\right\} _{\sigma =1}^{s}$, $\left\{ c_{\sigma }\right\} _{\sigma =1}^{s}$. It is worth to mention that a Courant–Friedrichs–Lewy (CFL) restriction is necessary when an explicit s-stage RK method is used in the DG framework. In order to present the RK discretization of the semi-discrete DGSEM (2.71), it is beneficial to write the method in the equivalent nodal representation. This representation is for all $i,j,k=0,\dots ,N$, given by

$$\begin{aligned} \frac{\partial \mathrm {J}_{ijk}}{\partial \tau }&={\mathsf {V}} \left( \left( \vec {\nu }\right) _{ijk}\right) , \end{aligned}$$

(2.103a)

$$\begin{aligned} \frac{\partial \left( \mathrm {J_{ijk}}{\mathbf {U}}_{ijk}\right) }{\partial \tau }\quad&=\quad {{\mathbf {\mathsf{{G}}}}}\left( \left( \vec {\nu }\right) _{ijk},{\mathbf {U}}_{ijk}\right) , \end{aligned}$$

(2.103b)

where the right hand sides are given by

$$\begin{aligned} {\mathsf {V}}\left( \left( \vec {\nu }\right) _{ijk}\right):= & {} \vec {{\mathbb {D}}}^{N}\!\cdot \vec {{\tilde{\nu }}}_{ijk}+\frac{1}{\omega _{i}\omega _{j}\omega _{k}}\int \limits _{\partial E,N}\ell _{i}\ell _{j}\ell _{k}\left( {\tilde{\nu }}_{{\hat{n}}}^{*} -{\tilde{\nu }}_{{\hat{n}}}\right) \,dS, \end{aligned}$$

(2.104)

$$\begin{aligned} {{\mathbf {\mathsf{{G}}}}}\left( \left( \vec {\nu }\right) _{ijk},{\mathbf {U}}_{ijk}\right):= & {} -\vec {{\mathbb {D}}}^{N}\!\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}{}_{ijk}^{\text {EC}} -\frac{1}{\omega _{i}\omega _{j}\omega _{k}}\int \limits _{\partial E,N}\ell _{i} \ell _{j}\ell _{k}\left( \tilde{{\mathbf {G}}}_{{\hat{n}}}^{*} -\tilde{{\mathbf {G}}}_{{\hat{n}}}\right) \,dS \end{aligned}$$

(2.105)

with the tensorial Lagrange polynomials $\ell _{i}\ell _{j}\ell _{k}$ given by (2.47).

It should be noted that the solutions $\mathrm {J}_{ijk}$, $i,j,k=0,\dots ,N$, of the ordinary differential equations (ODEs) (2.103a) need to be positive. We note that the solutions $\mathrm {J}_{ijk}$, $i,j,k=0,\dots ,N$ of the ODEs (2.103a) are not used to compute the volume weighted contravariant coordinate vectors ${\mathbb {J}}\vec {a}^{l}$, $l=1,2,3$, in the right hand sides (2.104) and (2.105). These vectors are computed from the mapping by the conservative curl form (2.52). Hence, the right hand sides (2.104) are are independent of $\mathrm {J}_{ijk}$, $i,j,k=0,\dots ,N$. Therefore, the solutions of the ODEs (2.103a) are positive, if the grid velocity does not cause to much distortion in the mesh which is ensured when the assumptions (A1)-(A3) are satisfied.

Next, the interval $\left[ 0,T\right]$ is divided in time points $t^{n}$. The step size of the time discretization is $\Delta t$. The DGSEM solutions, the fluxes and the grid velocity field are approximated in the time points $t^{n}$, e.g. ${\mathbf {U}}\left( t^{n}\right) \approx {\mathbf {U}}^{n}$. Then, the RK discretization of the semi-discrete DGSEM is given by

$$\begin{aligned}&\text {for }\varrho =1,\dots ,s: \nonumber \\&\mathrm {J}_{ijk}^{\left( \varrho \right) }=\mathrm {J}_{ijk}^{n}+\Delta t\sum _{\sigma =1}^{\varrho -1}a_{\varrho \sigma }{\mathsf {V}} \left( \left( \vec {\nu }\right) _{ijk}^{n+\sigma }\right) , \end{aligned}$$

(2.106a)

$$\begin{aligned}&{\mathbf {U}}_{ijk}^{\left( \varrho \right) }={\mathbf {U}}_{ijk}^{n}+\frac{\Delta t}{\mathrm {J}_{ijk}^{\left( \varrho \right) }}\sum _{\sigma =1}^{\varrho -1} a_{\varrho \sigma }\,\left( {{\mathbf {\mathsf{{G}}}}} \left( \left( \vec {\nu }\right) _{ijk}^{n+\sigma },{\mathbf {U}}_{ijk}^{(\sigma )} \right) -{\mathsf {V}}\left( \left( \vec {\nu }\right) _{ijk}^{n+\sigma } \right) {\mathbf {U}}_{ij}^{n}\right) , \end{aligned}$$

(2.106b)

$$\begin{aligned}&\mathrm {J}_{ijk}^{n+1}=\mathrm {J}_{ijk}^{n}+\Delta t\sum _{\sigma =1}^{s}b_{\sigma } {\mathsf {V}}\left( \left( \vec {\nu }\right) _{ijk}^{n+\sigma }\right) , \end{aligned}$$

(2.106c)

$$\begin{aligned}&{\mathbf {U}}_{ijk}^{n+1}={\mathbf {U}}_{ijk}^{n}+\frac{\Delta t}{\mathrm {J}_{ijk}^{\left( n+1\right) }}\sum _{\sigma =1}^{s}b_{\sigma }\, \left( {{\mathbf {\mathsf{{G}}}}}\left( \left( \vec {\nu }\right) _{ijk}^{n+\sigma }, {\mathbf {U}}_{ijk}^{(\sigma )}\right) -{\mathsf {V}}\left( \left( \vec {\nu } \right) _{ijk}^{n+\sigma }\right) {\mathbf {U}}_{ijk}^{n}\right) , \end{aligned}$$

(2.106d)

where $\left( \vec {\nu }\right) _{ijk}^{n+\sigma }:=\vec {\nu }\left( \xi _{i}^{1},\xi _{j}^{2},\xi _{k}^{3},t^{n}+c_{\sigma }\Delta t\right)$ and $\left\{ \xi _{i}^{1}\right\} _{i=0}^{N}$, $\left\{ \xi _{i}^{2}\right\} _{i=0}^{N}$, $\left\{ \xi _{i}^{3}\right\} _{i=0}^{N}$ are sets of LGL points. Next, we prove that the fully-discrete split form RK-DGSEM (2.106) satisfies the free stream preservation property.

Theorem 2.8

Suppose the fully-discrete split form RK-DGSEM (2.106) is investigated with periodic boundary conditions and the solution of the scheme is given by ${\mathbf {U}}_{ijk}^{n}={\mathbf {C}}:=\left( c_{1},\dots ,c_{p}\right) ^{T}\in {\mathbb {R}}^{p}$ for all elements $e_{\kappa }(t^{n})$, $\kappa =1,\dots ,K$, and the numerical fluxes satisfy (2.65). Then, the constant states $c_{l}$, $l=1,\dots ,p$, are preserved in each Runge–Kutta stage (2.106b). In particular, the solution of the fully-discrete DGSEM method at time level $t^{n+1}$ is ${\mathbf {U}}_{ijk}^{n+1}={\mathbf {C}}$.

Proof

Let $\varrho \in \left\{ 1,\dots ,s\right\}$ be an arbitrary fixed index. We are interested to investigate the $\varrho$-th RK stage. Hence, without loss of generality, we can assume that $\mathbf{U} ^{(\sigma )}=\mathbf{C}$ for all $\sigma =0,\dots ,\varrho -1$. Then, since the flux $\overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}}$ satisfies (2.65), it follows

$$\begin{aligned} \begin{aligned} \vec {{\mathbb {D}}}^{N}\!\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}{}_{ijk}^{\text {EC}}&= 2\sum _{m=0}^{N}{\mathcal {D}}_{im}\{\!\{{\mathbb {J}} \vec {a}^{1}\}\!\} _{\left( i,m\right) jk}\cdot \overset{\leftrightarrow }{{\mathbf {F}}} \left( {\mathbf {C}}\right) \\&\quad + 2\sum _{m=0}^{N}{\mathcal {D}}_{jm}\{\!\{{\mathbb {J}}\vec {a}^{2}\}\!\} _{i \left( j,m\right) k}\cdot \overset{\leftrightarrow }{{\mathbf {F}}}\left( {\mathbf {C}}\right) \\&\quad +2\sum _{m=0}^{N}{\mathcal {D}}_{km}\{\!\{{\mathbb {J}}\vec {a}^{3}\}\!\} _{ij \left( k,m\right) }\cdot \overset{\leftrightarrow }{{\mathbf {F}}}\left( {\mathbf {C}}\right) - \vec {{\mathbb {D}}}^{N}\!\cdot \left( \vec {{\tilde{\nu }}}\right) _{_{ijk}}^{n+\sigma }{\mathbf {C}}. \end{aligned} \end{aligned}$$

(2.107)

Furthermore, since the metric terms are computed by the conservative curl form (2.52), we obtain

$$\begin{aligned} \begin{aligned}&2\sum _{m=0}^{N}\left( {\mathcal {D}}_{im}\{\!\{{\mathbb {J}} \vec {a}^{1}\}\!\} _{\left( i,m\right) jk}+{\mathcal {D}}_{jm}\{\!\{{\mathbb {J}} \vec {a}^{2}\}\!\} _{i\left( j,m\right) k}+{\mathcal {D}}_{km}\{\!\{{\mathbb {J}} \vec {a}^{3}\}\!\} _{ij\left( k,m\right) }\right) \\&\quad = \sum _{m=0}^{N}\left( {\mathcal {D}}_{im}\left( {\mathbb {J}} \vec {a}^{1}\right) _{mjk}+{\mathcal {D}}_{jm}\left( {\mathbb {J}}\vec {a}^{2}\right) _{imk} +{\mathcal {D}}_{km}\left( {\mathbb {J}}\vec {a}^{3}\right) _{ijm}\right) =0. \end{aligned} \end{aligned}$$

(2.108)

Here we used the split form Lemma from Gassner et al. [23, Lemma 1] in the first step and in the second step we used the identity (2.60) for the discrete metric identities. Thus, it follows that

$$\begin{aligned} \vec {{\mathbb {D}}}^{N}\!\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}{}_{ijk}^{\text {EC}} =-\vec {{\mathbb {D}}}^{N}\!\cdot \left( \vec {{\tilde{\nu }}}\right) _{_{ijk}}^{n+\sigma }{\mathbf {C}}. \end{aligned}$$

(2.109)

Similar, since the flux $\overset{\leftrightarrow }{{\mathbf {G}}}{}^{*}$ satisfies (2.65), follows

$$\begin{aligned} \begin{aligned} \tilde{{\mathbf {G}}}_{{\hat{n}}}^{*}-\tilde{{\mathbf {G}}}_{{\hat{n}}}&= \sum _{l=1}^{3}{\hat{s}}n_{l}\left( {\mathbf {F}}_{l}\left( {\mathbf {C}}\right) -\{\!\{\nu _{l}^{n+\sigma }\}\!\} {\mathbf {C}}\right) -\left( {\hat{s}}\vec {n}\right) \cdot \left( \overset{\leftrightarrow }{{\mathbf {F}}}\left( {\mathbf {C}}\right) -\left( \vec {\nu } \right) ^{n+\sigma }{\mathbf {C}}\right) \\&= -\left( {\hat{s}}\vec {n}\right) \cdot \left( \{\!\{\left( \vec {\nu } \right) ^{n+\sigma }\}\!\} -\left( \vec {\nu }\right) ^{n+\sigma }\right) {\mathbf {C}} =-\left( {\tilde{\nu }}_{{\hat{n}}}^{*,n+\sigma }-{\tilde{\nu }}_{{\hat{n}}}^{n+\sigma } \right) {\mathbf {C}}. \end{aligned} \end{aligned}$$

(2.110)

Thus, the Eqs. (2.109) and (2.110) give

$$\begin{aligned} {{\mathbf {\mathsf{{G}}}}}\left( \left( \vec {\nu }\right) _{ijk}^{n+\sigma }, {\mathbf {C}}\right)= & {} \left( \vec {{\mathbb {D}}}^{N}\!\cdot \left( \vec {{\tilde{\nu }}} \right) _{_{ijk}}^{n+\sigma }+\frac{1}{\omega _{i}\omega _{j}\omega _{k}}\int \limits _{\partial E,N}\ell _{i}\ell _{j}\ell _{k}\left( {\tilde{\nu }}_{{\hat{n}}}^{*,n+\sigma }-{\tilde{\nu }}_{{\hat{n}}}^{n+\sigma }\right) \,dS\right) {\mathbf {C}}\nonumber \\= & {} {\mathsf {V}}\left( \left( \vec {\nu }\right) _{ijk}^{n+\sigma }\right) {\mathbf {C}}. \end{aligned}$$

(2.111)

Hence, the solution of the RK stage (2.106b) is given by

$$\begin{aligned} {\mathbf {U}}_{ijk}^{\left( \varrho \right) }={\mathbf {C}}+\frac{\Delta t}{\mathrm {J}_{ijk}^{\left( \varrho \right) }}\sum _{\sigma =1}^{\varrho -1} a_{\varrho \sigma }\,\left( {{\mathbf {\mathsf{{G}}}}}\left( \left( \vec {\nu } \right) _{ijk}^{n+\sigma },{\mathbf {C}}\right) -{\mathsf {V}} \left( \left( \vec {\nu }\right) _{ijk}^{n+\sigma }\right) {\mathbf {C}}\right) ={\mathbf {C}}. \end{aligned}$$

(2.112)

Since the parameter $\varrho$ was arbitrary chosen, it follows ${\mathbf {U}}_{ijk}^{\left( \varrho \right) }$ for all $\varrho =1,\dots ,s$. In particular, it follows

$$\begin{aligned} {\mathbf {U}}_{ijk}^{n+1}={\mathbf {C}}+\frac{\Delta t}{\mathrm {J}_{ijk}^{n+1}}\sum _{\sigma =1}^{s}b_{\sigma }\,\left( {{\mathbf {\mathsf{{G}}}}}\left( \left( \vec {\nu }\right) _{ijk}^{n+\sigma },{\mathbf {C}}\right) -{\mathsf {V}}\left( \left( \vec {\nu }\right) _{ijk}^{n+\sigma }\right) {\mathbf {C}}\right) ={\mathbf {C}}. \end{aligned}$$

(2.113)

This completes the proof of Theorem 2.8. $\square$

3 Numerical Results

The numerical computations in this section are performed with the open source code FLEXI¹ and the three-dimensional high-order meshes for the simulations are generated with the open source tool HOPR.²

We present tests on three dimensional moving hexahedral curved meshes for the compressible Euler equations. Based on these tests we will evaluate the theoretical findings of the previous sections. The three dimensional compressible Euler equations are given by

$$\begin{aligned} \frac{\partial \mathbf{u} }{\partial t} + \vec {\nabla } \cdot {\overset{\leftrightarrow }{\mathbf{f }}}=\mathbf 0 . \end{aligned}$$

(3.1)

The state vector and the components of the block vector flux, ${\overset{\leftrightarrow }{\mathbf{f }}}$, are given by

$$\begin{aligned} {\mathbf {u}}=\begin{bmatrix}\rho \\ \rho u_{1}\\ \rho u_{2}\\ \rho u_{3}\\ E \end{bmatrix},\quad \mathbf{f} _{1}=\begin{bmatrix}\rho u_{1}\\ \rho u_{1}^{2}+p\\ \rho u_{1}u_{2}\\ \rho u_{1}u_{3}\\ \left( E+p\right) u_{1} \end{bmatrix},\quad \mathbf{f} _{2}=\begin{bmatrix}\rho u_{2}\\ \rho u_{1}u_{2}\\ \rho u_{2}^{2}+p\\ \rho u_{2}u_{3}\\ \left( E+p\right) u_{2} \end{bmatrix},\quad \mathbf{f} _{3}=\begin{bmatrix}\rho u_{3}\\ \rho u_{1}u_{3}\\ \rho u_{2}u_{3}\\ \rho u_{3}^{2}+p\\ \left( E+p\right) u_{3} \end{bmatrix}, \end{aligned}$$

(3.2)

where the conservative variables are the density $\rho$, the momentum $\rho \vec {u}=\left[ \rho u_{1},\rho u_{2},\rho u_{3}\right] ^{T}$ and the total energy E. In order to close the system, we assume an ideal gas such that the pressure is defined as

$$\begin{aligned} p = (\gamma -1)\left( E - \frac{\rho }{2}\left| \vec {u}\right| ^2\right) , \end{aligned}$$

(3.3)

where $\gamma$ is the adiabatic exponent. We choose $\gamma =1.4$ in the following experiments. The system (3.1) is investigated in the domain $\Omega =\left[ x_{\text {min}},x_{\text {max}}\right] ^3$. At initial time $t=0$ the domain is divided in K non-overlapping and conforming cartesian hexahedral elements $e_{\kappa }(0)$, $\kappa =1,\dots ,K$. For each element $e_{\kappa }(0)$, $\kappa = 1,\dots ,K$, the temporal distribution of a grid point

$$\begin{aligned} \vec {x}_{\kappa }\left( 0\right) =\left( x_{1}^{\kappa }\left( 0\right) , x_{2}^{\kappa }\left( 0\right) ,x_{3}^{\kappa }\left( 0\right) \right) ^{T}\in e_{\kappa }(0) \end{aligned}$$

(3.4)

is given by

$$\begin{aligned} \vec {x}_{\kappa }\left( t\right) =\vec {x}_{\kappa }\left( 0\right) +0.05 L \sin \left( 2\pi t\right) \sin \left( \frac{2\pi }{L}x_{1}^{\kappa }\left( 0\right) \right) \sin \left( \frac{2\pi }{L}x_{2}^{\kappa }\left( 0\right) \right) \sin \left( \frac{2\pi }{L}x_{3}^{\kappa }\left( 0\right) \right) ,\nonumber \\ \end{aligned}$$

(3.5)

where $L:=x_{\text {max}}-x_{\text {min}}$. In Fig. 2, we show a slice through a three dimensional mesh with $K=16^3$ elements at initial time and at its maximal distortion. The mesh velocity is calculated by exact differentiation of Eq. (3.5). Note that the formula (3.5) is a common way to construct a deforming domain. For instance, similar formulas were used for the DG methods in [37, 64] and the collocation method in [66]. Furthermore, the five stage fourth order low-storage two-register explicit RK method (RK4(3)5[2R+]) from Kennedy, Carpenter and Lewis [34, Section 3.4.] is used for the time-integration in the numerical experiments. The CFL restriction is computed as in [12]

$$\begin{aligned} \frac{\Delta t}{\underset{1\le \kappa \le K}{\min }\left| h_{\kappa }\left( t^{n}\right) \right| }\le \frac{C_{\text {CFL}}}{\left( 2N+1\right) \lambda _{\text {max}}}, \end{aligned}$$

(3.6)

where $h_{\kappa }\left( t^{n}\right)$ is the minimum element size of $e_{\kappa }(t^{n})$, $C_{\text {CFL}}\in \left( 0,1\right]$ and $\lambda _{\text {max}}$ is the largest advective wave speed at the current time level traveling in either the $x_{1},x_{2},x_{3}$-direction.

Fig. 2

A slice through a three dimensional mesh with $K=16^3$ elements at initial time (left) and at its maximal distortion (right)

3.1 Experimental Convergence Rates

In this section, we verify the high-order approximation of the moving DGSEM (2.71). For this purpose, we investigate the domain $\Omega =\left[ -1,1\right] ^3$ and apply the method of manufactured solutions. Thus, we assume a solution of the form

$$\begin{aligned} {\mathbf {U}}\left( \vec {x},t\right) =\begin{bmatrix}\rho \left( \vec {x},t\right) \\ \rho u_{1}\left( \vec {x},t\right) \\ \rho u_{2}\left( \vec {x},t\right) \\ \rho u_{3}\left( \vec {x},t\right) \\ E\left( \vec {x},t\right) \end{bmatrix}=\begin{bmatrix}2+0.1\sin \left( \pi (x_1+x_2+x_3 - 2 \cdot 0.3t\right) )\\ 2+0.1\sin \left( \pi (x_1+x_2+x_3 - 2 \cdot 0.3t)\right) \\ 2+0.1\sin \left( \pi (x_1+x_2+x_3 - 2 \cdot 0.3t)\right) \\ 2+0.1\sin \left( \pi (x_1+x_2+x_3 - 2 \cdot 0.3t)\right) \\ \left[ 2+0.1\sin \left( \pi (x_1+x_2+x_3 - 2 \cdot 0.3t)\right) \right] ^{2} \end{bmatrix}. \end{aligned}$$

(3.7)

We plug solution (3.7) into the Euler system and compute the residual using a computer algebra system. This term is used as a source term in our convergence tests. We note that this term is handled and discretized as a solution independent part in the numerical computation.

We run the convergence test with periodic boundary conditions. Furthermore, the moving mesh DGSEM (2.71) is applied with the flux function in Appendix B.1 as volume and surface flux. In addition, the surface flux is stabilized by the dissipation operator in Appendix B.3. Besides using the grid point distribution given in (3.5), we also compute static reference solutions, by setting the grid velocity to zero. In this case, the moving mesh DGSEM (2.71) degenerates to the split form DGSEM for static meshes [23, 24].

In Table 1, we list the experimental order of convergence (EOC) and $\mathrm {L}^{2}$ errors for the conservative variables that we obtain for polynomials with odd degree $N=3$ on a static mesh (top) and on a moving mesh (bottom). To calculate the $\mathrm {L}^{2}$ norm, we interpolate the polynomial solution to a higher degree (at least twice the degree of the solution) and perform integration on that higher degree. The convergence rates on the moving mesh are not as good as on a static mesh, which can be justified by the high distortion in the mesh from the grid point distribution formula (3.5). However, with an increasing number of elements the same convergence rates as on a static mesh are almost reached. Moreover, the experimental order of convergence (EOC) and $\mathrm {L}^{2}$ errors for the conservative variables that we obtain for polynomials with even degree $N=4$ are listed in the Table 2. We observe a similar behavior as for the odd degree $N=3$. This indicate the high-order approximation properties of the moving mesh DGSEM.

Table 1 Experimental order of convergence (EOC) and $\mathrm {L}^{2}$ errors at time $T=5$ for the Euler manufactured solution test (3.7)

Table 2 Experimental order of convergence (EOC) and $\mathrm {L}^{2}$ errors at time $T=5$ for the Euler manufactured solution test (3.7)

3.2 Entropy Analysis Validation

The three dimensional Euler equations (3.1) are equipped with the entropy/entropy flux pairs

$$\begin{aligned} s=-\frac{\rho \varsigma }{\gamma -1},\quad f_{l}^{s}=-\frac{\rho \varsigma u_{l}}{\gamma -1},\quad l=1,2,3, \end{aligned}$$

(3.8)

where $\varsigma =\log \left( p\rho ^{-\gamma }\right)$. We are interested in the behavior of the discrete entropy conservation error

$$\begin{aligned} \Delta _{S}(T)={\bar{S}}\left( T\right) -{\bar{S}}\left( 0\right) , \end{aligned}$$

(3.9)

where ${\bar{S}}\left( \cdot \right)$ is computed by (2.78). Therefore, we investigate the inviscid Taylor-Green vortex (TGV) test case [56] in the domain $\Omega =\left[ 0,2\pi \right] ^{3}$. The inviscid TGV can be a challenging test case regarding the robustness of a numerical scheme, partly because the dynamics produce arbitrarily small scales. The flow field is thus by design under-resolved, which makes it a suitable test case to investigate the entropy conservation properties of the scheme. The TGV evolves from the initial data

$$\begin{aligned} \begin{aligned} \rho&= 1, \\ \vec {u}&= \left[ \text {sin}\left( x_{1}\right) \text {cos}\left( x_{2} \right) \text {cos}\left( x_{3}\right) ,-\text {cos}\left( x_{1}\right) \text {sin}\left( x_{2}\right) \text {cos}\left( x_{3}\right) ,0\right] ^{T}, \\ p&= p_{0}+\frac{1}{16}\left( \text {cos}\left( 2x_{1}\right) +\text {cos} \left( 2x_{2}\right) \right) \left( \text {cos}\left( 2x_{3}\right) +2\right) . \end{aligned} \end{aligned}$$

(3.10)

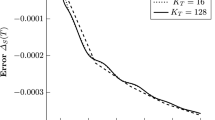
To render the simulation close to incompressible, the Mach number $M_0=\frac{1}{\sqrt{\gamma p_{0}}}$ is set to 0.1 by adjusting the pressure correspondingly. We run the simulation with $K=16^3$ elements and periodic boundary conditions. The final time is chosen to be $T=13$. Furthermore, we apply the flux function in Appendix B.1 to compute the derivative projection operator (2.64). To calculate the discrete integral entropy, the SBP mass matrices are used directly. In Fig. 3 we present a log-log plot of the entropy conservation error for $N=3,4$. We note that the flux in Appendix B.1 is used as surface flux without a dissipation term in these computations, rendering the semi-discrete discretization fully entropy conserving. As expected, we observe the reduction of the remaining entropy conservation error according to the order of the RK method for decreasing CFL numbers. In Fig. 4 the temporal evolution of the entropy conservation errors $\Delta _{S}(T)$ is given. The CFL number is set to $C_{\text {CFL}}=0.125$ and polynomial degrees $N=3$ and $N=4$ are used. We observe that the entropy conservation error $\Delta _{S}(T)$ is constant in time (dashed line) when the flux in Appendix B.1 is used without a dissipation term. This indicates the entropy conservation in the TVG test case. On the other hand the entropy conservation error $\Delta _{S}(T)$ is decreasing in time (solid line) when the surface flux is stabilized by the dissipation term in Appendix B.3. Thus, the moving mesh DGSEM is an entropy stable scheme in this test case. These observations agree with the results in Theorem 2.4 and Corollary 2.6.

Fig. 3

Log-log plot of the entropy conservation errors $\Delta _{S}(T)$ for the Euler equations with initial data (3.10). The errors are given at time $T=13$ for polynomials with degree $N=3$ (solid line) and $N=4$ (dotted line) on a curved moving mesh with $K=16^3$ elements

Fig. 4

Temporal evolution of the entropy conservation errors $\Delta _{S}(T)$ for the Euler equations with initial data (3.10). The flux in Appendix B.1 is used as surface flux without dissipation (solid line) and with the dissipation term in Appendix B.3 (dashed line)

3.3 Robustness Test

As has been stated in Sect. 3.2 and noted in literature [50, 62], the inviscid TGV is a notoriously challenging test case for the stability of the numerical scheme. While for lower polynomial degrees calculations may be possible, high-order simulations are known to crash even if aliasing-reducing methods like polynomial dealiasing are used [50]. Thus, we use the TGV test case (3.10) to demonstrate the increased robustness of the entropy stable moving mesh DGSEM. To do so, we run the simulation up to $T=13$ using a polynomial degree of $N=7$ on three different meshes employing $K_1=14^3$, $K_2=19^3$ and $K_3=26^3$ elements. These cases correspond to the most restrictive simulations from [50]. Again, the point distribution given in (3.5) is used. We use the flux function in Appendix B.1 as volume and surface flux and stabilize the surface flux by the dissipation operator in Appendix B.3.

Using the entropy stable moving DGSEM, we were able to run all simulations until final time. This shows that the consistent dissipation operators in combination with the entropy conservative volume fluxes can lead to superior stability properties. We note that simulations without dissipative surface fluxes crash before reaching the final time for higher-order simulations ($N\ge 3$). This highlights the role that entropy conservation plays in the stabilization of challenging numerical problems.

3.4 Free Stream Preservation Validation

We consider the Euler equations (3.1) on the domain $\Omega =[0,2\pi ]^3$ with the initial data

$$\begin{aligned} {\mathbf {U}}\left( x,t\right) =\begin{bmatrix}\rho \left( x,t\right) \\ \rho u_{1}\left( x,t\right) \\ \rho u_{2}\left( x,t\right) \\ \rho u_{3}\left( x,t\right) \\ E\left( x,t\right) \end{bmatrix}=\begin{bmatrix}1 \\ 0.3 \\ 0 \\ 0 \\ 17 \\ \end{bmatrix}. \end{aligned}$$

(3.11)

The entropy stable DGSEM is applied with the flux function in Appendix B.1 as volume and surface flux as well as the dissipation operator in Appendix B.3 to stabilize the surface flux. We apply $K=16^3$ elements, the formula (3.5) to describe the displacement of the mesh points and periodic boundary conditions are used in the simulation. Furthermore, the final time is set to $T=20$. In Table 3, we present the $\mathrm {L}^{\infty }$ errors between the initial data (3.11) and the numerical solution at time $T=20$ for polynomials of degree $N=3$ (top), $N=4$ (bottom) and different CFL numbers $C_{\text {CFL}}$. The errors are computed by super sampling the polynomial solution, at least doubling the amount of nodes per direction from the underlying solution. We observe that the errors are close to zero and vary slightly for the different CFL numbers. These results indicate the compliance of the free stream preservation property.

Table 3 Free stream preservation test for $N=3$ (top) and $N=4$ (bottom)

4 Conclusions

In this work a moving mesh DGSEM to solve non-linear conservation laws has been constructed and analyzed. The semi-discrete method is provably entropy stable and the free stream preservation property is satisfied for each explicit s-stage Runge–Kutta method.

The moving mesh DGSEM has been presented for three dimensional conservation laws. The derivatives in space are approximated with high-order derivative matrices which are SBP operators. Furthermore, the split form DG framework [23, 24] has been used to avoid aliasing in the discretization of the volume integrals. In addition, two-point flux functions with the generalized entropy condition (2.67) are used in the split form DG framework. These modules in the spatial discretization are the basis to prove that the moving mesh DGSEM is an entropy stable scheme, when periodic boundary conditions are used. Non-periodic boundary conditions require the construction of suitable dissipative boundary conditions to enforce the entropy stability. The discrete entropy analysis requires the assumptions that the time derivatives can be evaluated exactly and that properties like positivity preservation (of the water height, density or pressure) are satisfied on the discrete level. Operations like the integration-by-parts formula are mimicked by the SPB operators on the discrete level.

The three dimensional Euler equations have been considered to verify the proven properties of the moving mesh DGSEM in our numerical experiments. We presented convergence tests for smooth test problems to verify that the split form DG framework provides also on a moving mesh a high-order accurate approximation. Furthermore, the numerical robustness tests in the Sect. 3.3 emphasize the relevance of the entropy stable DGSEM, since the method was able to run the challenging inviscid TGV test case until final time.

Appendices

Proof for Lemma 2.1

In this section, we prove Lemma 2.1. For the sake of simplicity we present merely the proof in two dimensions. The three dimensional proof can be done by the same argumentation.

A way to compute the two dimensional bijective isoparametric transfinite mapping is given in the book of Kopriva [36, Chapter 6, equation (6.18)]. The mapping is for all $\left[ \xi ^{1},\xi ^{2}\right] ^{T}\in E$ and $\tau \in \left[ 0,T\right]$ given by

$$\begin{aligned} \begin{aligned} e_{\kappa }\left( t\right) \ni \vec {x}\left( t\right)&= \vec {\chi } \left( \xi ^{1},\xi ^{2},\tau \right) =\quad \frac{1}{2} \left[ \left( 1-\xi ^{1}\right) {\mathbb {I}}^{N}\!\left( \vec {\Gamma }_{4}\right) \left( \xi ^{2},\tau \right) +\left( 1+\xi ^{1}\right) {\mathbb {I}}^{N}\!\left( \vec {\Gamma }_{2}\right) \left( \xi ^{2},\tau \right) \right] \\&\quad +\frac{1}{2}\left[ \left( 1-\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \vec {\Gamma }_{1} \right) \left( \xi ^{1},\tau \right) +\left( 1+\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \vec {\Gamma }_{3}\right) \left( \xi ^{1},\tau \right) \right] \\&\quad -\frac{1}{4}\left[ \left( 1+\xi ^{1}\right) \left\{ \left( 1-\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \vec {\Gamma }_{1}\right) \left( 1,\tau \right) + \left( 1+\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \vec {\Gamma }_{3}\right) \left( 1,\tau \right) \right\} \right] \\&\quad -\frac{1}{4}\left[ \left( 1-\xi ^{1}\right) \left\{ \left( 1-\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \vec {\Gamma }_{1}\right) \left( -1,\tau \right) +\left( 1+\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \vec {\Gamma }_{3}\right) \left( -1,\tau \right) \right\} \right] . \end{aligned} \end{aligned}$$

(A.1)

It is worth to mention that the mapping $\vec {\chi }\left( \xi ^{1},\xi ^{2},\tau \right)$ matches with the boundary faces in the interpolation points. The location of the curved faces $\vec {\Gamma }_{1}\left( \xi ^{1},\tau \right)$, $\vec {\Gamma }_{2}\left( \xi ^{2},\tau \right)$, $\vec {\Gamma }_{3}\left( \xi ^{1},\tau \right)$ and $\vec {\Gamma }_{4}\left( \xi ^{2},\tau \right)$ is sketched in Fig. 5.

Fig. 5

Left the reference element $E=[-1,1]^2$ and on the right a general quadrilateral element $e_{k}(t)$ with the curved faces $\vec {\Gamma }_{1}\left( \xi ^{1},\tau \right)$, $\vec {\Gamma }_{2}\left( \xi ^{2},\tau \right)$, $\vec {\Gamma }_{3}\left( \xi ^{1},\tau \right)$ and $\vec {\Gamma }_{4}\left( \xi ^{2},\tau \right)$. The mapping $\vec {\chi }\left( \xi ^{1},\xi ^{2},\tau \right)$ connects E and $e_{k}(t)$

Fig. 6

Two elements $\varvec{e_{1}}(t)$ and $\varvec{e_{2}}(t)$ of a conforming mesh sharing the same curved boundary (dotted curve)

In the following, $e_{1}(t)$ and $e_{2}(t)$ are two neighboring elements which share the same boundary face. Without loss of generality the elements share the face $\vec {\Gamma }_{3}^{1}=\vec {\Gamma }_{1}^{2}$ as it is illustrated in Fig. 6. Then, for the elements $e_{l}(t)$, $l=1,2$, the grid velocity field is given by

$$\begin{aligned} \vec {\nu }^{l}\left( \xi ^{1},\xi ^{2},\tau \right)= & {} \frac{1}{2} \left[ \left( 1-\xi ^{1}\right) {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau } \vec {\Gamma }_{4}^{l}\right) \left( \xi ^{2},\tau \right) +\left( 1+\xi ^{1}\right) {\mathbb {I}}^{N}\!\left( \frac{d}{dt}\vec {\Gamma }_{2}^{l}\right) \left( \xi ^{2},t\right) \right] \nonumber \\&+\frac{1}{2}\left[ \left( 1-\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau } \vec {\Gamma }_{1}^{l}\right) \left( \xi ^{1},\tau \right) +\left( 1+\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau }\vec {\Gamma }_{3}^{l}\right) \left( \xi ^{1},\tau \right) \right] \nonumber \\&-\frac{1}{4}\left[ \left( 1+\xi ^{1}\right) \left\{ \left( 1-\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau }\vec {\Gamma }_{1}^{l}\right) \left( 1,\tau \right) \right. \right. \nonumber \\&\left. \left. +\left( 1+\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau } \vec {\Gamma }_{3}^{l}\right) \left( 1,\tau \right) \right\} \right] \nonumber \\&-\frac{1}{4}\left[ \left( 1-\xi ^{1}\right) \left\{ \left( 1-\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau } \vec {\Gamma }_{1}^{l}\right) \left( -1,\tau \right) \right. \right. \nonumber \\&\left. \left. +\left( 1+\xi ^{2}\right) {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau }\vec {\Gamma }_{3}^{l}\right) \left( -1,\tau \right) \right\} \right] , \end{aligned}$$

(A.2)

since it holds the identity

$$\begin{aligned} \frac{\partial }{\partial \tau }{\mathbb {I}}^{N}\!\left( \vec {\Gamma }_{i}^{l}\right) = {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau }\vec {\Gamma }_{i}^{l}\right) ,\quad l=1,2,\quad \text {and}\quad i=1,2,3,4. \end{aligned}$$

(A.3)

Furthermore, since for $l=1,2$, and $i=1,2,3,4$, the faces $\vec {\Gamma }_{i}^{l}\left( \cdot ,\cdot ,t\right)$ are continuously differentiable in the time interval $\left[ 0,T\right]$, it holds

$$\begin{aligned} {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau }\vec {\Gamma }_{4}^{1}\right) \left( 1,\tau \right)&= {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau } \vec {\Gamma }_{3}^{1}\right) \left( -1,\tau \right) ,\quad {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau }\vec {\Gamma }_{2}^{1}\right) \left( 1,\tau \right) ={\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau } \vec {\Gamma }_{3}^{1}\right) \left( 1,\tau \right) , \end{aligned}$$

(A.4)

$$\begin{aligned} {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau }\vec {\Gamma }_{4}^{2}\right) \left( -1,\tau \right)&= {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau } \vec {\Gamma }_{1}^{2}\right) \left( -1,\tau \right) ,\quad {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau }\vec {\Gamma }_{2}^{2}\right) \left( -1,\tau \right) = {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau }\vec {\Gamma }_{1}^{2}\right) \left( 1,\tau \right) , \end{aligned}$$

(A.5)

$$\begin{aligned} \frac{\partial }{\partial \tau }\vec {\Gamma }_{3}^{1}\left( \zeta _{j},\tau \right)&= \frac{d}{dt}\vec {\Gamma }_{1}^{2}\left( \zeta _{j},\tau \right) ,\quad j=0,\dots ,N, \end{aligned}$$

(A.6)

where $\left\{ \zeta _{j}\right\} _{j=0}^{N}$ are interpolation points.

For the element $e_{1}(t)$ the points along the interface with $e_{2}(t)$ are mapped in the set $\left\{ \left( \xi ,1\right) :\ \xi \in \left[ -1,1\right] \right\}$. Hence, the grid velocity becomes

$$\begin{aligned} \begin{aligned} \vec {\nu }^{1}\left( \xi ,1,\tau \right)&= {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau }\vec {\Gamma }_{3}^{1}\right) \left( \xi ,\tau \right) ,\quad \forall \xi \in \left[ -1,1\right] \end{aligned} \end{aligned}$$

(A.7)

by (A.4). On the opposite, for the element $e_{2}(t)$ the points along the interface with $e_{1}(t)$ are mapped in the set $\left\{ \left( \xi ,-1\right) :\ \xi \in \left[ -1,1\right] \right\}$ and we obtain

$$\begin{aligned} \begin{aligned} \vec {\nu }^{2}\left( \xi ,-1,\tau \right)&= {\mathbb {I}}^{N}\!\left( \frac{\partial }{\partial \tau }\vec {\Gamma }_{1}^{2}\right) \left( \xi ,\tau \right) ,\quad \forall \xi \in \left[ -1,1\right] , \end{aligned} \end{aligned}$$

(A.8)

by (A.5). Thus, we obtain $\vec {\nu }^{1}\left( \cdot ,1,\tau \right) =\vec {\nu }^{2}\left( \cdot ,-1,\tau \right)$ by (A.6). This proves that the grid velocity is continuous in the interface points of the two neighboring elements.

Entropy Stable Moving Mesh Euler Fluxes

We present entropy stable Cartesian fluxes ${\mathbf {G}}_{l}^{\text {EC}}$, $l=1,2,3$, for the compressible Euler equations (3.1) equipped with the entropy/entropy flux pairs (3.8). Then the entropy variables are given by

$$\begin{aligned} {\mathbf {w}}=\left[ \frac{\gamma -\varsigma }{\gamma -1}-\beta \left| \vec {u} \right| ^{2},2\beta u_{1},2\beta u_{2},2\beta u_{3},-2\beta \right] ^{T},\quad \text {with}\quad \beta :=\frac{\rho }{2p} \end{aligned}$$

(B.1)

and the entropy functionals are given by

$$\begin{aligned} \phi ={\mathbf {w}}^{T}{\mathbf {u}}-s=\rho ,\quad \psi _{l}={\mathbf {w}}^{T} {\mathbf {f}}_{l}-f_{l}^{s}=\rho u_{l},\quad l=1,2,3. \end{aligned}$$

(B.2)

1.1 Entropy Conservative Euler Flux Based on the Flux in [8]

In the following the logarithmic mean $\{\!\{\cdot \}\!\} ^{\text {log}}$ will be used. For two positive states $a^{-}$ and $a^{+}$, the logarithmic mean is defined by

$$\begin{aligned} \{\!\{a\}\!\} ^{\text {log}}:={\left\{ \begin{array}{ll} \frac{[\![a]\!] }{[\![\log \left( a\right) ]\!] }, &{} \text {if }\,a^{-}\ne a^{+},\\ a^{-}, &{} \text {if }a^{-}=a^{+}. \end{array}\right. } \end{aligned}$$

(B.3)

A numerically stable procedure to compute the logarithmic mean (B.3) is provided by Ismail and Roe [33, Appendix B]. Friedrich et al. [21, Theorem 3] constructed the following state function

$$\begin{aligned} {\mathbf {U}}^{\#}=\begin{bmatrix}\{\!\{\rho \}\!\} ^{\text {log}}\\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{2}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{3}\}\!\} \\ \frac{\{\!\{\rho \}\!\} ^{\text {log}}}{2\left( \gamma -1\right) \{\!\{\beta \}\!\} ^{\text {log}}} +\frac{1}{2}\{\!\{\rho \}\!\} ^{\text {log}}\overline{\left| \vec {u}\right| ^{2}} \end{bmatrix}, \end{aligned}$$

(B.4)

where

$$\begin{aligned} \overline{\left| \vec {u}\right| ^{2}}=2\left( \{\!\{u_{1}\}\!\} ^{2}+\{\!\{u_{2}\}\!\} ^{2} +\{\!\{u_{3}\}\!\} ^{2}\right) -\left( \{\!\{u_{1}^{2}\}\!\} +\{\!\{u_{2}^{2}\}\!\} +\{\!\{u_{3}^{2}\}\!\} \right) . \end{aligned}$$

(B.5)

The state function (B.4) is consistent, symmetric and it holds

$$\begin{aligned}{}[\![{\mathbf {w}}]\!] ^{T}{\mathbf {U}}^{\#}=[\![\rho ]\!] =[\![\phi ]\!] . \end{aligned}$$

(B.6)

In [40, Eg. (3.4) p. 1974] LeFloch et al. gave a general formula to compute entropy conservative numerical state flux-functions. Furthermore, Chandrashekar constructed in [8] a kinetic energy preserving and entropy conservative (KEPEC) numerical flux function for the compressible Euler equations. In the $x_{1}$-direction Chandrashekar’s KEPEC flux is given by

$$\begin{aligned} {\mathbf {F}}_{1}^{\text {EC}\_\text {CH}}=\begin{bmatrix}\{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}\}\!\} ^{2}+\frac{\{\!\{\rho \}\!\} }{2\{\!\{\beta \}\!\} }\\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}\}\!\} \{\!\{u_{2}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}\}\!\} \{\!\{u_{3}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}\}\!\} \left( \frac{1}{2\left( \gamma -1\right) \{\!\{\beta \}\!\} ^{\text {log}}}+\frac{1}{2}\overline{\left| \vec {u}\right| ^{2}}\right) +\frac{\{\!\{\rho \}\!\} \{\!\{u_{1}\}\!\} }{2\{\!\{\beta \}\!\} } \end{bmatrix}. \end{aligned}$$

(B.7)

The flux (B.7) is consistent with $\mathbf{f} _1$ and symmetric. In particular, Chandrashekar proved that

$$\begin{aligned}{}[\![{\mathbf {w}}]\!] ^{T}{\mathbf {F}}_{1}^{\text {EC}\_\text {CH}}=[\![\rho u_{1}]\!] =[\![\psi _{1}]\!] . \end{aligned}$$

(B.8)

The state function (B.4) and the flux function (B.7) are used to construct the flux

$$\begin{aligned} {\mathbf {G}}_{1}^{\text {EC}\_\text {CH}}={\mathbf {F}}_{1}^{\text {EC}\_\text {CH}} -\{\!\{\nu _{1}\}\!\} {\mathbf {U}}^{\#}=\begin{bmatrix}\{\!\{\rho \}\!\} ^{\text {log}} \{\!\{u_{1}-\nu _{1}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}-\nu _{1}\}\!\} \{\!\{u_{1}\}\!\} +\frac{\{\!\{\rho \}\!\} }{2\{\!\{\beta \}\!\} }\\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}-\nu _{1}\}\!\} \{\!\{u_{2}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}-\nu _{1}\}\!\} \{\!\{u_{3}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}-\nu _{1}\}\!\} \left( \frac{1}{2 \left( \gamma -1\right) \{\!\{\beta \}\!\} ^{\text {log}}}+\frac{1}{2} \overline{\left| \vec {u}\right| ^{2}}\right) +\frac{\{\!\{\rho \}\!\} \{\!\{u_{1}\}\!\} }{2\{\!\{\beta \}\!\} } \end{bmatrix}.\nonumber \\ \end{aligned}$$

(B.9)

The flux (B.9) is consistent with ${\mathbf {g}}_{1}={\mathbf {f}}_{1}-\nu _{1}{\mathbf {u}}$, symmetric and it follows

$$\begin{aligned}{}[\![{\mathbf {w}}]\!] ^{T}{\mathbf {G}}_{1}^{\text {EC}\_\text {CH}}=[\![{\mathbf {w}}]\!] ^{T} {\mathbf {F}}_{1}^{\text {EC}\_\text {CH}}-\{\!\{\nu _{1}\}\!\} [\![{\mathbf {w}}]\!] ^{T} {\mathbf {U}}^{\#}=[\![\psi _{1}]\!] -\{\!\{\nu _{1}\}\!\} [\![\phi ]\!] \end{aligned}$$

(B.10)

by (B.6) and (B.8). In the same way, the $x_{2}$-direction and the $x_{3}$-direction of Chandrashekar’s KEPEC flux can be used to construct

$$\begin{aligned} {\mathbf {G}}_{2}^{\text {EC}\_\text {CH}}=\begin{bmatrix}\{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{2}-\nu _{2}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}\}\!\} \{\!\{u_{2}-\nu _{2}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{2}\}\!\} \{\!\{u_{2}-\nu _{2}\}\!\} +\frac{\{\!\{\rho \}\!\} }{2\{\!\{\beta \}\!\} }\\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{2}-\nu _{2}\}\!\} \{\!\{u_{3}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{2}-\nu _{2}\}\!\} \left( \frac{1}{2\left( \gamma -1\right) \{\!\{\beta \}\!\} ^{\text {log}}}+\frac{1}{2}\overline{\left| \vec {u}\right| ^{2}}\right) +\frac{\{\!\{\rho \}\!\} \{\!\{u_{2}\}\!\} }{2\{\!\{\beta \}\!\} } \end{bmatrix} \end{aligned}$$

(B.11)

and

$$\begin{aligned} {\mathbf {G}}_{3}^{\text {EC}\_\text {CH}}=\begin{bmatrix}\{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{3}-\nu _{3}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}\}\!\} \{\!\{u_{3}-\nu _{3}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{2}\}\!\} \{\!\{u_{3}-\nu _{3}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{3}\}\!\} \{\!\{u_{3}-\nu _{3}\}\!\} +\frac{\{\!\{\rho \}\!\} }{2\{\!\{\beta \}\!\} }\\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{3}-\nu _{3}\}\!\} \left( \frac{1}{2\left( \gamma -1\right) \{\!\{\beta \}\!\} ^{\text {log}}}+\frac{1}{2}\overline{\left| \vec {u}\right| ^{2}}\right) +\frac{\{\!\{\rho \}\!\} \{\!\{u_{3}\}\!\} }{2\{\!\{\beta \}\!\} } \end{bmatrix}. \end{aligned}$$

(B.12)

The fluxes (B.11), (B.12) are consistent with ${\mathbf {g}}_{2}={\mathbf {f}}_{2}-\nu _{2}{\mathbf {u}}$, ${\mathbf {g}}_{3}={\mathbf {f}}_{3}-\nu _{3}{\mathbf {u}}$, symmetric and satisfy

$$\begin{aligned}{}[\![{\mathbf {w}}]\!] ^{T}{\mathbf {G}}_{2}^{\text {EC}\_\text {CH}}&= [\![{\mathbf {w}}]\!] ^{T} {\mathbf {F}}_{2}^{\text {EC}\_\text {CH}}-\{\!\{\nu _{2}\}\!\} [\![{\mathbf {w}}]\!] ^{T} {\mathbf {U}}^{\#}=[\![\psi _{2}]\!] -\{\!\{\nu _{2}\}\!\} [\![\phi ]\!] , \end{aligned}$$

(B.13)

$$\begin{aligned}{}[\![{\mathbf {w}}]\!] ^{T}{\mathbf {G}}_{3}^{\text {EC}\_\text {CH}}&= [\![{\mathbf {w}}]\!] ^{T} {\mathbf {F}}_{3}^{\text {EC}\_\text {CH}}-\{\!\{\nu _{3}\}\!\} [\![{\mathbf {w}}]\!] ^{T} {\mathbf {U}}^{\#}=[\![\psi _{3}]\!] -\{\!\{\nu _{3}\}\!\} [\![\phi ]\!] . \end{aligned}$$

(B.14)

1.2 Entropy Conservative Euler Flux Based on the Flux in [55]

Ranocha constructed in his PHD thesis [55] another KEPEC numerical flux for the compressible Euler equations. We proceed as in the Appendix  B.1 and use the state (B.4) and Ranocha’s flux to construct the following two-point flux functions

$$\begin{aligned} {\mathbf {G}}_{1}^{\text {EC}\_\text {R}}= & {} \begin{bmatrix}\{\!\{\rho \}\!\} ^{\text {log}} \{\!\{u_{1}-\nu _{1}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}-\nu _{1}\}\!\} \{\!\{u_{1}\}\!\} +\{\!\{p\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}-\nu _{1}\}\!\} \{\!\{u_{2}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}-\nu _{1}\}\!\} \{\!\{u_{3}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}-\nu _{1}\}\!\} \left( \frac{1}{2\left( \gamma -1\right) \{\!\{\beta \}\!\} ^{\text {log}}}+\frac{1}{2}\overline{\left| \vec {u}\right| ^{2}}\right) +2\{\!\{p\}\!\} \{\!\{u_{1}\}\!\} -\{\!\{pu_{1}\}\!\} \end{bmatrix}, \qquad \qquad \end{aligned}$$

(B.15a)

$$\begin{aligned} {\mathbf {G}}_{2}^{\text {EC}\_\text {R}}= & {} \begin{bmatrix}\{\!\{\rho \}\!\} ^{\text {log}} \{\!\{u_{2}-\nu _{2}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}\}\!\} \{\!\{u_{2}-\nu _{2}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{2}\}\!\} \{\!\{u_{2}-\nu _{2}\}\!\} +\{\!\{p\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{2}-\nu _{2}\}\!\} \{\!\{u_{3}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{2}-\nu _{2}\}\!\} \left( \frac{1}{2 \left( \gamma -1\right) \{\!\{\beta \}\!\} ^{\text {log}}}+\frac{1}{2} \overline{\left| \vec {u}\right| ^{2}}\right) +2\{\!\{p\}\!\} \{\!\{u_{2}\}\!\} -\{\!\{pu_{2}\}\!\} \end{bmatrix}, \end{aligned}$$

(B.15b)

and

$$\begin{aligned} {\mathbf {G}}_{3}^{\text {EC}\_\text {R}}=\begin{bmatrix}\{\!\{\rho \}\!\} ^{\text {log}} \{\!\{u_{3}-\nu _{3}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{1}\}\!\} \{\!\{u_{3}-\nu _{3}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{2}\}\!\} \{\!\{u_{3}-\nu _{3}\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{3}\}\!\} \{\!\{u_{3}-\nu _{3}\}\!\} +\{\!\{p\}\!\} \\ \{\!\{\rho \}\!\} ^{\text {log}}\{\!\{u_{3}-\nu _{3}\}\!\} \left( \frac{1}{2\left( \gamma -1\right) \{\!\{\beta \}\!\} ^{\text {log}}}+\frac{1}{2}\overline{\left| \vec {u}\right| ^{2}} \right) +2\{\!\{p\}\!\} \{\!\{u_{3}\}\!\} -\{\!\{pu_{3}\}\!\} \end{bmatrix}.\nonumber \\ \end{aligned}$$

(B.15c)

The flux functions (B.15) are consistent with ${\mathbf {g}}_{1}$, ${\mathbf {g}}_{2}$, ${\mathbf {g}}_{3}$, symmetric and satisfy

$$\begin{aligned}{}[\![{\mathbf {w}}]\!] ^{T}{\mathbf {G}}_{l}^{\text {EC}\_\text {R}}=[\![\psi _{l}]\!] - \{\!\{\nu _{l}\}\!\} [\![\phi ]\!] ,\quad l=1,2,3. \end{aligned}$$

(B.16)

1.3 Matrix Dissipation Term for the Euler Flux

We will use the Euler fluxes from the previous Appendices B.1 and B.2 with the dissipation operators form Winters et al. [63]. In the following, the matrices to construct the entropy stable dissipation operators (2.96) are listed. The average components of the dissipation term in the $x_{1}$-direction are given by

$$\begin{aligned} \mathcal {\mathcal {R}}_{1}^{\star }= & {} \begin{bmatrix}1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ \{\!\{u_{1}\}\!\} -{\bar{c}} &{}\quad \{\!\{u_{1}\}\!\} &{}\quad 0 &{}\quad 0 &{}\quad \{\!\{u_{1}\}\!\} +{\bar{c}}\\ \{\!\{u_{2}\}\!\} &{}\quad \{\!\{u_{2}\}\!\} &{}\quad 1 &{}\quad 0 &{}\quad \{\!\{u_{2}\}\!\} \\ \{\!\{u_{3}\}\!\} &{} \quad \{\!\{u_{3}\}\!\} &{}\quad 0 &{}\quad 1 &{} \quad \{\!\{u_{3}\}\!\} \\ {\bar{h}}-\{\!\{u_{1}\}\!\} {\bar{c}} &{}\quad \frac{1}{2}\overline{\left| \vec {u}\right| ^{2}} &{}\quad \{\!\{u_{2}\}\!\} &{}\quad \{\!\{u_{3}\}\!\} &{}\quad {\bar{h}}+\{\!\{u_{1}\}\!\} {\bar{c}} \end{bmatrix}, \end{aligned}$$

(B.17)

$$\begin{aligned} \mathcal {\mathcal {T}}_{1}^{\star }= & {} \text {diag}\left( \sqrt{\frac{\{\!\{\rho \}\!\} ^{\text {log}}}{2\gamma }},\sqrt{\frac{\left( \gamma -1\right) }{\gamma }\{\!\{\rho \}\!\} ^{\text {log}}}, \sqrt{\frac{\{\!\{\rho \}\!\} }{2\{\!\{\beta \}\!\} }},\sqrt{\frac{\{\!\{\rho \}\!\} }{2\{\!\{\beta \}\!\} }}, \sqrt{\frac{\{\!\{\rho \}\!\} ^{\text {log}}}{2\gamma }}\right) , \end{aligned}$$

(B.18)

$$\begin{aligned} \Lambda _{1}= & {} \text {diag}\left( \left| \{\!\{u_{1}-\nu _{1}\}\!\} -{\bar{c}}\right| , \left| \{\!\{u_{1}-\nu _{1}\}\!\} \right| ,\left| \{\!\{u_{1}-\nu _{1}\}\!\} \right| , \left| \{\!\{u_{1}-\nu _{1}\}\!\} \right| ,\left| \{\!\{u_{1}-\nu _{1}\}\!\} +{\bar{c}}\right| \right) ,\nonumber \\ \end{aligned}$$

(B.19)

where

$$\begin{aligned} {\bar{c}}:=\sqrt{\frac{\gamma \{\!\{\rho \}\!\} }{2\{\!\{\rho \}\!\} ^{\text {log}}\{\!\{\beta \}\!\} }}, \quad {\bar{h}}:=\frac{\gamma }{2\left( \gamma -1\right) \{\!\{\beta \}\!\} ^{\text {log}}}+ \frac{1}{2}\overline{\left| \vec {u}\right| ^{2}}. \end{aligned}$$

(B.20)

In the $x_{2}$-direction the components are given by

$$\begin{aligned} \mathcal {\mathcal {R}}_{2}^{\star }= & {} \begin{bmatrix}1 &{} \quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1\\ \{\!\{u_{1}\}\!\} &{}\quad 1 &{} \quad \{\!\{u_{1}\}\!\} &{}\quad 0 &{}\quad \{\!\{u_{1}\}\!\} \\ \{\!\{u_{2}\}\!\} -{\bar{c}} &{}\quad 0 &{}\quad \{\!\{u_{2}\}\!\} &{}\quad 0 &{}\quad \{\!\{u_{2}\}\!\} +{\bar{c}}\\ \{\!\{u_{3}\}\!\} &{}\quad 0 &{}\quad \{\!\{u_{3}\}\!\} &{}\quad 1 &{}\quad \{\!\{u_{3}\}\!\} \\ {\bar{h}}-\{\!\{u_{2}\}\!\} {\bar{c}} &{}\quad \{\!\{u_{1}\}\!\} &{}\quad \frac{1}{2}\overline{\left| \vec {u}\right| ^{2}} &{}\quad \{\!\{u_{3}\}\!\} &{}\quad {\bar{h}}+\{\!\{u_{2}\}\!\} {\bar{c}} \end{bmatrix}, \end{aligned}$$

(B.21)

$$\begin{aligned} \mathcal {\mathcal {T}}_{2}^{\star }= & {} \text {diag}\left( \sqrt{\frac{\{\!\{\rho \}\!\} ^{\text {log}}}{2\gamma }}, \sqrt{\frac{\{\!\{\rho \}\!\} }{2\{\!\{\beta \}\!\} }},\sqrt{\frac{\left( \gamma -1\right) }{\gamma } \{\!\{\rho \}\!\} ^{\text {log}}},\sqrt{\frac{\{\!\{\rho \}\!\} }{2\{\!\{\beta \}\!\} }}, \sqrt{\frac{\{\!\{\rho \}\!\} ^{\text {log}}}{2\gamma }}\right) , \end{aligned}$$

(B.22)

$$\begin{aligned} \Lambda _{2}= & {} \text {diag}\left( \left| \{\!\{u_{2}-\nu _{2}\}\!\} -{\bar{c}}\right| , \left| \{\!\{u_{2}-\nu _{2}\}\!\} \right| ,\left| \{\!\{u_{2}-\nu _{2}\}\!\} \right| , \left| \{\!\{u_{2}-\nu _{2}\}\!\} \right| ,\left| \{\!\{u_{2}-\nu _{2}\}\!\} +{\bar{c}}\right| \right) ,\nonumber \\ \end{aligned}$$

(B.23)

and in the $x_{3}$-direction the components are given by

$$\begin{aligned} \mathcal {\mathcal {R}}_{3}^{\star }= & {} \begin{bmatrix}1 &{} \quad 0 &{} \quad 0 &{} \quad 1 &{} \quad 1\\ \{\!\{u_{1}\}\!\} &{} \quad 1 &{} \quad 0 &{} \quad \{\!\{u_{1}\}\!\} &{} \quad \{\!\{u_{1}\}\!\} \\ \{\!\{u_{2}\}\!\} &{} \quad 0 &{} \quad 1 &{} \quad \{\!\{u_{2}\}\!\} &{} \quad \{\!\{u_{2}\}\!\} \\ \{\!\{u_{3}\}\!\} -{\bar{c}} &{} \quad 0 &{} \quad 0 &{} \quad \{\!\{u_{3}\}\!\} &{} \quad \{\!\{u_{3}\}\!\} +{\bar{c}}\\ {\bar{h}}-\{\!\{u_{3}\}\!\} {\bar{c}} &{} \quad \{\!\{u_{1}\}\!\} &{} \quad \{\!\{u_{2}\}\!\} &{} \quad \frac{1}{2}\overline{\left| \vec {u}\right| ^{2}} &{} \quad {\bar{h}}+\{\!\{u_{3}\}\!\} {\bar{c}} \end{bmatrix}, \end{aligned}$$

(B.24)

$$\begin{aligned} \mathcal {\mathcal {T}}_{3}^{\star }= & {} \text {diag}\left( \sqrt{\frac{\{\!\{\rho \}\!\} ^{\text {log}}}{2\gamma }}, \sqrt{\frac{\{\!\{\rho \}\!\} }{2\{\!\{\beta \}\!\} }},\sqrt{\frac{\{\!\{\rho \}\!\} }{2\{\!\{\beta \}\!\} }}, \sqrt{\frac{\left( \gamma -1\right) }{\gamma }\{\!\{\rho \}\!\} ^{\text {log}}}, \sqrt{\frac{\{\!\{\rho \}\!\} ^{\text {log}}}{2\gamma }}\right) , \end{aligned}$$

(B.25)

$$\begin{aligned} \Lambda _{3}= & {} \text {diag}\left( \left| \{\!\{u_{3}-\nu _{3}\}\!\} -{\bar{c}}\right| , \left| \{\!\{u_{3}-\nu _{3}\}\!\} \right| ,\left| \{\!\{u_{3}-\nu _{3}\}\!\} \right| , \left| \{\!\{u_{3}-\nu _{3}\}\!\} \right| ,\left| \{\!\{u_{3}-\nu _{3}\}\!\} +{\bar{c}}\right| \right) .\nonumber \\ \end{aligned}$$

(B.26)

Proofs of Entropy Conservation for Advection Terms

In this section, we apply the following identities which result from the properties of the SBP operator $\mathcal {\mathcal {Q}}$

$$\begin{aligned} \sum _{i,j=0}^{N}\mathcal {\mathcal {Q}}_{ij}[\![a]\!] _{\left( i,j\right) }\{\!\{b\}\!\} _{\left( i,j\right) }&= \sum _{i,j=0}^{N}\mathcal {\mathcal {Q}}_{ij}a_{i}b_{j}-\left( a_{N}b_{N}-a_{0}b_{0}\right) , \end{aligned}$$

(C.1)

$$\begin{aligned} \sum _{i,j=0}^{N}\mathcal {\mathcal {Q}}_{ij}[\![a]\!] _{\left( i,j\right) }\{\!\{b\}\!\} _{\left( i,j\right) }\{\!\{c\}\!\} _{\left( i,j\right) }&= \sum _{i,j=0}^{N}2\mathcal {\mathcal {Q}}_{ij}a_{i}\{\!\{b\}\!\} _{\left( i,j\right) }\{\!\{c\}\!\} _{\left( i,j\right) }-\left( a_{N}b_{N}c_{N}-a_{0}b_{0}c_{0}\right) , \end{aligned}$$

(C.2)

where $\left\{ a\right\} _{i=0}^{N}$, $\left\{ b\right\} _{i=0}^{N}$ and $\left\{ c\right\} _{i=0}^{N}$ are generic nodal values. These identities can be proven in a similar way as the discrete split forms in Lemma 1 in [23]. Thus, we skip a proof in this paper.

1.1 Proof for Eq. (2.84)

The flux $\overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}}$ satisfies the symmetry property (2.66) and the SBP property (2.59) provides

$$\begin{aligned} 2\omega _{i}{\mathcal {D}}_{im}=2{\mathcal {Q}}_{im}={\mathcal {Q}}_{im}- {\mathcal {Q}}_{mi}+{\mathcal {B}}_{im},\quad i,m=0,\dots ,N. \end{aligned}$$

(C.3)

Thus, we obtain

$$\begin{aligned} \begin{aligned}&\left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}{}^{\text {EC}}, {\mathbf {W}}\right\rangle _{N}\\&\quad = \sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m,k=0}^{N}{\mathcal {Q}}_{im} [\![{\mathbf {W}}]\!] _{\left( i,m\right) j}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{mjk}\right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{1}\}\!\} _{\left( i,m\right) jk}\right) \\&\qquad +\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m=0}^{N}{\mathcal {B}}_{im} {\mathbf {W}}_{ijk}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{mjk} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{1}\}\!\} _{\left( i,m\right) jk}\right) \\&\qquad +\sum _{i,k=0}^{N}\omega _{i}\omega _{k}\sum _{j,m=0}^{N}{\mathcal {Q}}_{jm} [\![{\mathbf {W}}]\!] _{i\left( j,m\right) ,k}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{imk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{imk} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{2}\}\!\} _{i\left( j,m\right) k}\right) \\&\qquad +\sum _{i,k=0}^{N}\omega _{i}\omega _{k}\sum _{j,m=0}^{N}{\mathcal {B}}_{jm} {\mathbf {W}}_{ijk}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{imk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{imk} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{2}\}\!\} _{i\left( j,m\right) k}\right) \\&\qquad +\sum _{i,j=0}^{N}\omega _{i}\omega _{j}\sum _{j,m=0}^{N}{\mathcal {Q}}_{km} [\![{\mathbf {W}}]\!] _{ij\left( k,m\right) }^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{ijm},{\mathbf {U}}_{ijk},{\mathbf {U}}_{ijm} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{3}\}\!\} _{ij\left( k,m\right) }\right) \\&\qquad +\sum _{i,j=0}^{N}\omega _{i}\omega _{j}\sum _{j,m=0}^{N}{\mathcal {B}}_{km} {\mathbf {W}}_{ijk}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{ijm},{\mathbf {U}}_{ijk},{\mathbf {U}}_{ijm} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{3}\}\!\} _{ij\left( k,m\right) }\right) \end{aligned} \end{aligned}$$

(C.4)

by the same calculation as in [21, Appendix C.1., Equations (C.4) and (C.5)] or [24, Appendix B.3., Equation (B.31)]. To evaluate the fluxes $\overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}}$ at the element interfaces, we apply the consistence condition (2.65), such that e.g.

$$\begin{aligned}&\overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}}\left( \vec {\nu }_{Njk},\vec {\nu }_{Njk}, {\mathbf {U}}_{Njk},{\mathbf {U}}_{Njk}\right) =\overset{\leftrightarrow }{{\mathbf {F}}} \left( {\mathbf {U}}_{Njk}\right) -\{\!\{\vec {\nu }\}\!\} _{\left( N,N\right) jk} {\mathbf {U}}_{Njk}=\overset{\leftrightarrow }{{\mathbf {G}}}_{Njk},\nonumber \\&\quad j,k=0,\dots ,N. \end{aligned}$$

(C.5)

This provides the identity

$$\begin{aligned}&\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m=0}^{N}{\mathcal {B}}_{im} {\mathbf {W}}_{ijk}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{mjk} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{1}\}\!\} _{\left( i,m\right) jk}\right) \nonumber \\&\qquad +\sum _{i,k=0}^{N}\omega _{i}\omega _{k}\sum _{j,m=0}^{N}{\mathcal {B}}_{jm} {\mathbf {W}}_{ijk}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{imk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{imk} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{2}\}\!\} _{i\left( j,m\right) k}\right) \nonumber \\&\qquad +\sum _{i,j=0}^{N}\omega _{i}\omega _{j}\sum _{k,m=0}^{N}{\mathcal {B}}_{km} {\mathbf {W}}_{ijk}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{ijm},{\mathbf {U}}_{ijk},{\mathbf {U}}_{ijm} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{3}\}\!\} _{ij\left( k,m\right) }\right) \nonumber \\&\quad = \sum _{j,k=0}^{N}\omega _{j}\omega _{k}\left[ {\mathbf {W}}_{Njk}^{T} \left( \overset{\leftrightarrow }{{\mathbf {G}}}_{Njk}\cdot \left( {\mathbb {J}}\vec {a}^{1} \right) _{Njk}\right) -{\mathbf {W}}_{0jk}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}_{0jk} \cdot \left( {\mathbb {J}}\vec {a}^{1}\right) _{0jk}\right) \right] \nonumber \\&\qquad +\sum _{i,k=0}^{N}\omega _{i}\omega _{k}\left[ {\mathbf {W}}_{iNk}^{T} \left( \overset{\leftrightarrow }{{\mathbf {G}}}_{iNk}\cdot \left( {\mathbb {J}}\vec {a}^{2} \right) _{iNk}\right) -{\mathbf {W}}_{i0k}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}_{i0k} \cdot \left( {\mathbb {J}}\vec {a}^{2}\right) _{i0k}\right) \right] \nonumber \\&\qquad +\sum _{i,j=0}^{N}\omega _{i}\omega _{j}\left[ {\mathbf {W}}_{ijN}^{T} \left( \overset{\leftrightarrow }{{\mathbf {G}}}_{ijN}\cdot \left( {\mathbb {J}}\vec {a}^{3} \right) _{ijN}\right) -{\mathbf {W}}_{ij0}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}_{ij0} \cdot \left( {\mathbb {J}}\vec {a}^{3}\right) _{ij0}\right) \right] \nonumber \\&\quad =\int \limits _{\partial E,N}{\mathbf {W}}^{T}\left\{ \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}\cdot {\hat{n}}\right\} \,dS. \end{aligned}$$

(C.6)

Next, we investigate the first sum on the right hand side in the Eq. (C.4). Since the fluxes ${\mathbf {G}}_{l}^{\text {EC}}$, $l=1,2,3$, satisfy the entropy condition (2.67), follows

$$\begin{aligned} \begin{aligned}&\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m=0}^{N}{\mathcal {Q}}_{im} [\![{\mathbf {W}}]\!] _{\left( i,m\right) jk}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{mjk} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{1}\}\!\} _{\left( i,m\right) jk}\right) \\&\quad =\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m=0}^{N}{\mathcal {Q}}_{im} [\![{\mathbf {W}}]\!] _{\left( i,m\right) jk}^{T}{\mathbf {G}}_{1}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{mjk} \right) \{\!\{{\mathbb {J}}a_{1}^{1}\}\!\} _{\left( i,m\right) jk} \\&\qquad +\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m=0}^{N}{\mathcal {Q}}_{im} [\![{\mathbf {W}}]\!] _{\left( i,m\right) jk}^{T}{\mathbf {G}}_{2}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{mjk} \right) \{\!\{{\mathbb {J}}a_{2}^{1}\}\!\} _{\left( i,m\right) jk} \\&\qquad +\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m=0}^{N}{\mathcal {Q}}_{im} [\![{\mathbf {W}}]\!] _{\left( i,m\right) jk}^{T}{\mathbf {G}}_{3}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{mjk} \right) \{\!\{{\mathbb {J}}a_{3}^{1}\}\!\} _{\left( i,m\right) jk}\\&\quad =\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m=0}^{N}{\mathcal {Q}}_{im} \left( [\![\Psi _{1}]\!] _{\left( i,m\right) jk}-\{\!\{\nu _{1}\}\!\} _{\left( i,m\right) jk} [\![\Phi ]\!] _{\left( i,m\right) jk}\right) \{\!\{{\mathbb {J}}a_{1}^{1}\}\!\} _{\left( i,m\right) jk} \\&\qquad +\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m=0}^{N}{\mathcal {Q}}_{im} \left( [\![\Psi _{2}]\!] _{\left( i,m\right) jk}-\{\!\{\nu _{2}\}\!\} _{\left( i,m\right) jk} [\![\Phi ]\!] _{\left( i,m\right) jk}\right) \{\!\{{\mathbb {J}}a_{2}^{1}\}\!\} _{\left( i,m\right) jk} \\&\qquad +\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m=0}^{N}{\mathcal {Q}}_{im} \left( [\![\Psi _{3}]\!] _{\left( i,m\right) jk}-\{\!\{\nu _{3}\}\!\} _{\left( i,m\right) jk} [\![\Phi ]\!] _{\left( i,m\right) jk}\right) \{\!\{{\mathbb {J}}a_{3}^{1}\}\!\} _{\left( i,m\right) jk}. \end{aligned} \end{aligned}$$

(C.7)

For $l=1,2,3$, the SPB properties (C.1) and (C.2) provide

$$\begin{aligned}&\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m=0}^{N}{\mathcal {Q}}_{im} \left( [\![\Psi _{l}]\!] _{\left( i,m\right) jk}-\{\!\{\nu _{l}\}\!\} _{\left( i,m\right) jk} [\![\Phi ]\!] _{\left( i,m\right) jk}\right) \{\!\{{\mathbb {J}}a_{l}^{1}\}\!\} _{\left( i,m\right) jk} \nonumber \\&\quad = -\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\left[ \left( \left( \Psi _{l}\right) _{Njk}- \left( \nu _{l}\right) _{Njk}\Phi _{Njk}\right) \left( {\mathbb {J}}a_{l}^{1}\right) _{Njk}\right. \nonumber \\&\qquad \left. - \left( \left( \Psi _{l}\right) _{0jk}-\left( \nu _{l}\right) _{0jk}\Phi _{0jk}\right) \left( {\mathbb {J}}a_{l}^{1}\right) _{0jk}\right] \nonumber \\&\qquad +\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\left( \Psi _{l}\right) _{ijk} \sum _{m=0}^{N}{\mathcal {D}}_{im}\left( {\mathbb {J}}a_{l}^{1}\right) _{mjk}\nonumber \\&\qquad - \sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\Phi _{ijk}\sum _{m=0}^{N}2\,{\mathcal {D}}_{im}\{\!\{\nu _{l}\}\!\} _{\left( i,m\right) jk}\{\!\{{\mathbb {J}}a_{l}^{1}\}\!\} _{\left( i,m\right) jk}. \end{aligned}$$

(C.8)

Hence, we obtain the identity

$$\begin{aligned} \begin{aligned}&\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\sum _{i,m=0}^{N}{\mathcal {Q}}_{im} [\![{\mathbf {W}}]\!] _{\left( i,m\right) jk}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{mjk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{mjk} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{1}\}\!\} _{\left( i,m\right) jk}\right) \\&\quad =-\sum _{j,k=0}^{N}\omega _{j}\omega _{k}\left[ \left( \left( \vec {\Psi } \right) _{Njk}-\left( \vec {\nu }\right) _{Njk}\Phi _{Njk}\right) \cdot \left( {\mathbb {J}}\vec {a}^{1}\right) _{Njk}-\left( \left( \vec {\Psi }\right) _{0jk}\right. \right. \\&\qquad \left. \left. - \left( \vec {\nu }\right) _{0jk}\Phi _{0jk}\right) \left( {\mathbb {J}}\vec {a}^{1} \right) _{0jk}\right] \\&\qquad +\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\left( \vec {\Psi } \right) _{ijk}\cdot \left( \sum _{m=0}^{N}{\mathcal {D}}_{im}\left( {\mathbb {J}} \vec {a}^{1}\right) _{mjk}\right) \\&\qquad -\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\Phi _{ijk} \sum _{m=0}^{N}2\,{\mathcal {D}}_{im}\{\!\{\vec {\nu }\}\!\} _{\left( i,m\right) jk} \cdot \{\!\{{\mathbb {J}}\vec {a}^{1}\}\!\} _{\left( i,m\right) jk}. \end{aligned} \end{aligned}$$

(C.9)

By the same computation, the third sum on the right hand side in the Eq. (C.4) becomes

$$\begin{aligned} \begin{aligned}&\sum _{i,k=0}^{N}\omega _{i}\omega _{k}\sum _{j,m=0}^{N}{\mathcal {Q}}_{jm} [\![{\mathbf {W}}]\!] _{i\left( j,m\right) k}^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{imk},{\mathbf {U}}_{ijk},{\mathbf {U}}_{imk} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{2}\}\!\} _{i\left( j,m\right) k}\right) \\&\quad = -\sum _{i,k=0}^{N}\omega _{i}\omega _{k}\left[ \left( \left( \vec {\Psi }\right) _{iNk}- \left( \vec {\nu }\right) _{iNk}\Phi _{iNk}\right) \cdot \left( {\mathbb {J}}\vec {a}^{2} \right) _{iNk}-\left( \left( \vec {\Psi }\right) _{i0k}\right. \right. \\&\qquad \left. \left. -\left( \vec {\nu }\right) _{i0k} \Phi _{i0k}\right) \left( {\mathbb {J}}\vec {a}^{2}\right) _{i0k}\right] \\&\qquad +\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\left( \vec {\Psi }\right) _{ijk} \cdot \left( \sum _{m=0}^{N}{\mathcal {D}}_{jm}\left( {\mathbb {J}}\vec {a}^{2} \right) _{imk}\right) \\&\qquad -\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\Phi _{ijk}\sum _{m=0}^{N} 2\,{\mathcal {D}}_{jm}\{\!\{\vec {\nu }\}\!\} _{i\left( j,m\right) k}\cdot \{\!\{{\mathbb {J}}\vec {a}^{2}\}\!\} _{i\left( j,m\right) k} \end{aligned} \end{aligned}$$

(C.10)

and the sum next-to-last on the right hand side in the Eq. (C.4) becomes

$$\begin{aligned}&\sum _{i,j=0}^{N}\omega _{i}\omega _{j}\sum _{k,m=0}^{N}{\mathcal {Q}}_{km} [\![{\mathbf {W}}]\!] _{ij\left( k,m\right) }^{T}\left( \overset{\leftrightarrow }{{\mathbf {G}}}{}^{\text {EC}} \left( \vec {\nu }_{ijk},\vec {\nu }_{ijm},{\mathbf {U}}_{ijk},{\mathbf {U}}_{ijm} \right) \cdot \{\!\{{\mathbb {J}}\vec {a}^{3}\}\!\} _{ij\left( k,m\right) }\right) \nonumber \\&\quad = -\sum _{i,j=0}^{N}\omega _{i}\omega _{j}\left[ \left( \left( \vec {\Psi } \right) _{ijN}-\left( \vec {\nu }\right) _{ijN}\Phi _{ijN}\right) \cdot \left( {\mathbb {J}}\vec {a}^{3}\right) _{ijN}-\left( \left( \vec {\Psi } \right) _{ij0}\right. \right. \nonumber \\&\qquad \left. \left. -\left( \vec {\nu }\right) _{ij0}\Phi _{ij0}\right) \left( {\mathbb {J}}\vec {a}^{3}\right) _{ij0}\right] \nonumber \\&\qquad +\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\left( \vec {\Psi } \right) _{ijk}\cdot \left( \sum _{m=0}^{N}{\mathcal {D}}_{km} \left( {\mathbb {J}}\vec {a}^{3}\right) _{ijm}\right) \nonumber \\&\qquad -\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\Phi _{ijk} \sum _{m=0}^{N}2\,{\mathcal {D}}_{km}\{\!\{\vec {\nu }\}\!\} _{ij\left( k,m\right) } \cdot \{\!\{{\mathbb {J}}\vec {a}^{3}\}\!\} _{ij\left( k,m\right) }. \end{aligned}$$

(C.11)

The definition of the derivative projection operator (2.62) in the Eq. (2.71a) provides

$$\begin{aligned} \begin{aligned}&-\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\Phi _{ijk}\sum _{m=0}^{N}2\, {\mathcal {D}}_{im}\{\!\{\vec {\nu }\}\!\} _{\left( i,m\right) jk}\cdot \{\!\{{\mathbb {J}} \vec {a}^{1}\}\!\} _{\left( i,m\right) jk} \\&\qquad -\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\Phi _{ijk} \sum _{m=0}^{N}2\,{\mathcal {D}}_{jm}\{\!\{\vec {\nu }\}\!\} _{i\left( j,m\right) k} \cdot \{\!\{{\mathbb {J}}\vec {a}^{2}\}\!\} _{i\left( j,m\right) k}\\&\qquad -\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\Phi _{ijk} \sum _{m=0}^{N}2\,{\mathcal {D}}_{km}\{\!\{\vec {\nu }\}\!\} _{ij\left( k,m\right) } \cdot \{\!\{{\mathbb {J}}\vec {a}^{3}\}\!\} _{ij\left( k,m\right) }\\&\quad =-\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\Phi _{ijk} \left( \vec {{\mathbb {D}}}^{N}\!\cdot \vec {{\tilde{\nu }}}_{ijk}\right) =-\left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \vec {{\tilde{\nu }}},\Phi \right\rangle _{N}. \end{aligned} \end{aligned}$$

(C.12)

Next, we plug the Eqs. (C.6), (C.9), (C.10), (C.11) in the Eq. (C.4) and apply the identity (C.12). This results in the identity

$$\begin{aligned} \begin{aligned} \left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}{}^{\text {EC}},{\mathbf {W}}\right\rangle _{N}&= \int \limits _{\partial E,N}\left[ {\mathbf {W}}^{T}\left\{ \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}\cdot {\hat{n}}\right\} -\left( \vec {{\tilde{\Psi }}}-\vec {{\tilde{\nu }}}\Phi \right) \cdot {\hat{n}}\right] \,dS -\left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \vec {{\tilde{\nu }}},\Phi \right\rangle _{N} \\&\quad +\sum _{i,j,k=0}^{N}\omega _{i}\omega _{j}\omega _{k}\left( \vec {\Psi } \right) _{ijk}\cdot \left( \sum _{m=0}^{N}\left( {\mathcal {D}}_{im} \left( {\mathbb {J}}\vec {a}^{1}\right) _{mjk}+{\mathcal {D}}_{jm} \left( {\mathbb {J}}\vec {a}^{2}\right) _{imk}\right. \right. \\&\quad \left. \left. +{\mathcal {D}}_{km} \left( {\mathbb {J}}\vec {a}^{3}\right) _{ijm}\right) \right) . \end{aligned} \end{aligned}$$

(C.13)

The definition of the contravariant vector flux functions (2.23) and contravariant block vector flux functions (2.28) provide the equality

$$\begin{aligned} \begin{aligned} {\mathbf {W}}^{T}\left\{ \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}\cdot {\hat{n}}\right\} -\left( \vec {{\tilde{\Psi }}}-\vec {{\tilde{\nu }}}\Phi \right) \cdot {\hat{n}}&= \sum _{l,r=1}^{3}{\mathbb {J}}a_{l}^{r}\left( {\mathbf {W}}^{T}{\mathbf {G}}_{l} -\mathbf {\Psi }_{l}+\nu _{l}\Phi \right) {\hat{n}}^{r} \\&= \sum _{l,r=1}^{3}{\mathbb {J}}a_{l}^{r}\left( F_{l}^{s}-\nu _{l}S \right) {\hat{n}}^{r} \\&= \left( {\hat{s}}\vec {n}\right) \cdot \left( \vec {F}^{s}-\vec {\nu }S\right) = \tilde{F}_{{\hat{n}}}^{s}-{\tilde{\nu }}_{{\hat{n}}}S. \end{aligned} \end{aligned}$$

(C.14)

Therefore, the Eq. (C.13) simplifies to

$$\begin{aligned} \left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \overset{\leftrightarrow }{\tilde{{\mathbf {G}}}}{}^{\text {EC}},{\mathbf {W}}\right\rangle _{N} =\int \limits _{\partial E,N}\left( \tilde{F}_{{\hat{n}}}^{s}-{\tilde{\nu }}_{{\hat{n}}}S\right) \,dS-\left\langle \vec {{\mathbb {D}}}^{N}\!\cdot \vec {{\tilde{\nu }}},\Phi \right\rangle _{N}, \end{aligned}$$

(C.15)

since the discrete volume weighted contravariant vectors ${\mathbb {J}}\vec {a}^{\alpha }$, $\alpha =1,2,3$, are computed by the conservative curl form (2.52) and the discrete metric identities (2.60) are satisfied in the LGL points.