An Entropy Stable h / p Non-Conforming Discontinuous Galerkin Method with the Summation-by-Parts Property

Abstract

This work presents an entropy stable discontinuous Galerkin (DG) spectral element approximation for systems of non-linear conservation laws with general geometric (h) and polynomial order (p) non-conforming rectangular meshes. The crux of the proofs presented is that the nodal DG method is constructed with the collocated Legendre–Gauss–Lobatto nodes. This choice ensures that the derivative/mass matrix pair is a summation-by-parts (SBP) operator such that entropy stability proofs from the continuous analysis are discretely mimicked. Special attention is given to the coupling between non-conforming elements as we demonstrate that the standard mortar approach for DG methods does not guarantee entropy stability for non-linear problems, which can lead to instabilities. As such, we describe a precise procedure and modify the mortar method to guarantee entropy stability for general non-linear hyperbolic systems on h / p non-conforming meshes. We verify the high-order accuracy and the entropy conservation/stability of fully non-conforming approximation with numerical examples.

Appendices

A Derivations of the Growth of Primary Quantities and Entropy

The proof below is the same result as presented by Fisher et al. [12]. For completeness, we re-derive the proof in our notation. We analyze the two dimensional discretization of (1.27) on a single element.

$$\begin{aligned} J\omega _i\omega _j\left( \varvec{U}_{t}\right) _{ij}+\omega _j\mathcal {L}(\varvec{U}_{ij})_x+\omega _i\mathcal {L}(\varvec{U}_{ij})_y=0, \end{aligned}$$

(A.1)

with

$$\begin{aligned} \begin{aligned} \mathcal {L}(\varvec{U}_{ij})_x&=2\sum _{m=0}^N\omega _i\mathsf {D}_{im}\tilde{\varvec{F}}^{\mathrm {EC}}(\varvec{U}_{ij},\varvec{U}_{mj})-\left( \delta _{iN}[\tilde{\varvec{F}}-\tilde{\varvec{F}}^{\mathrm {EC}}]_{Nj}-\delta _{i0}[\tilde{\varvec{F}}-\tilde{\varvec{F}}^{\mathrm {EC}}]_{0j}\right) ,\\ \mathcal {L}(\varvec{U}_{ij})_y&=2\sum _{m=0}^N\omega _j\mathsf {D}_{jm}\tilde{\varvec{G}}^{\mathrm {EC}}(\varvec{U}_{ij},\varvec{U}_{im})-\left( \delta _{Nj}[\tilde{\varvec{G}}-\tilde{\varvec{G}}^{\mathrm {EC}}]_{iN}-\delta _{0j}[\tilde{\varvec{G}}-\tilde{\varvec{G}}^{\mathrm {EC}}]_{i0}\right) . \end{aligned} \end{aligned}$$

(A.2)

Assuming, that $\tilde{\varvec{F}}^{\mathrm {EC}}$ and $\tilde{\varvec{G}}^{\mathrm {EC}}$ satisfy the appropriate entropy condition (1.24)

$$\begin{aligned} \begin{aligned} \tilde{\varvec{F}}^{\mathrm {EC}}(\varvec{U}_{ij},\varvec{U}_{ml})^T\left( \varvec{V}_{ij}-\varvec{V}_{ml}^{q}\right) =\tilde{{\varPsi }}^f_{ij}-\tilde{{\varPsi }}^f_{ml},\\ \tilde{\varvec{G}}^{\mathrm {EC}}(\varvec{U}_{ij},\varvec{U}_{ml})^T\left( \varvec{V}_{ij}-\varvec{V}_{ml}^{q}\right) =\tilde{{\varPsi }}^g_{ij}-\tilde{{\varPsi }}^g_{ml}. \end{aligned} \end{aligned}$$

(A.3)

First, we derive the growth of the primary quantities on each element $E_k, k=1,\ldots ,K$. Summing over all nodes $i,j=0,\ldots ,N$ yields

$$\begin{aligned} \underbrace{J\sum _{i,j=0}^N\omega _i\omega _j\left( \varvec{U}_{t}\right) _{ij}}_{\approx \int \varvec{U}_t \,\mathrm {d}E}+\sum _{j=0}^N\omega _j\sum _{i=0}^N\mathcal {L}(\varvec{U}_{ij})_x+\sum _{i=0}^N\omega _i\sum _{j=0}^N\mathcal {L}(\varvec{U}_{ij})_y=0, \end{aligned}$$

(A.4)

with

$$\begin{aligned} \sum _{i=0}^N\mathcal {L}(\varvec{U}_{ij})_x=2\sum _{i=0}^N\sum _{m=0}^N{\mathsf {Q}}_{im}\tilde{\varvec{F}}^{\mathrm {EC}}(\varvec{U}_{ij},\varvec{U}_{mj})-[\tilde{\varvec{F}}-\tilde{\varvec{F}}^{\mathrm {EC}}]_{Nj}+[\tilde{\varvec{F}}-\tilde{\varvec{F}}^{\mathrm {EC}}]_{0j}. \end{aligned}$$

(A.5)

Using the SBP property of the matrices $2{\mathsf {Q}}={\mathsf {Q}}-{\mathsf {Q}}^T+{\mathsf {B}}$ we find

$$\begin{aligned} \sum _{i=0}^N\mathcal {L}(\varvec{U}_{ij})_x=\sum _{i=0}^N\sum _{m=0}^N {\mathsf {Q}}_{im}\tilde{\varvec{F}}^{\mathrm {EC}}(\varvec{U}_{ij},\varvec{U}_{mj})-\sum _{i=0}^N\sum _{m=0}^N{\mathsf {Q}}_{im}\tilde{\varvec{F}}^{\mathrm {EC}}(\varvec{U}_{mj},\varvec{U}_{ij})+\tilde{\varvec{F}}^{\mathrm {EC}}_{Nj}-\tilde{\varvec{F}}^{\mathrm {EC}}_{0j}. \end{aligned}$$

(A.6)

Due to nearly skew-symmetric nature of ${\mathsf {Q}}$ we arrive at

$$\begin{aligned} \sum _{i=0}^N\mathcal {L}(\varvec{U}_{ij})_x=\tilde{\varvec{F}}^{\mathrm {EC}}_{Nj}-\tilde{\varvec{F}}^{\mathrm {EC}}_{0j}. \end{aligned}$$

(A.7)

And similar for $\sum \limits _{j=0}^N\mathcal {L}(\varvec{U}_{ij})_y$ we have

$$\begin{aligned} \sum _{j=0}^N\mathcal {L}(\varvec{U}_{ij})_x=\tilde{\varvec{G}}^{\mathrm {EC}}_{iN}-\tilde{\varvec{G}}^{\mathrm {EC}}_{i0}. \end{aligned}$$

(A.8)

Together both directions yield

$$\begin{aligned} \underbrace{J\sum _{i,j=0}^N\omega _i\omega _j\left( \varvec{U}_{t}\right) _{ij}}_{\approx \int \varvec{U}_t \,\mathrm {d}E}=-\sum _{j=0}^N\omega _j\left( \tilde{\varvec{F}}^{\mathrm {EC}}_{Nj}-\tilde{\varvec{F}}^{\mathrm {EC}}_{0j}\right) -\sum _{i=0}^N\omega _i\left( \tilde{\varvec{G}}^{\mathrm {EC}}_{iN}-\tilde{\varvec{G}}^{\mathrm {EC}}_{i0}\right) , \end{aligned}$$

(A.9)

which is precisely (2.5).

Next, we derive the entropy growth on the single element. To do so, we pre-multiply with the entropy variables and sum over all nodes to get

$$\begin{aligned} J\sum _{i,j=0}^N\omega _i\omega _j\underbrace{\varvec{V}_{ij}^T\left( \varvec{U}_{t}\right) _{ij}}_{=:\left( S_{t}\right) _{ij}}+\sum _{j=0}^N\omega _j\sum _{i=0}^N\varvec{V}_{ij}^T\mathcal {L}(\varvec{U}_{ij})_x + \sum _{i=0}^N\omega _j\sum _{j=0}^N\varvec{V}_{ij}^T\mathcal {L}(\varvec{U}_{ij})_y=0, \end{aligned}$$

(A.10)

with

$$\begin{aligned} \begin{aligned} \sum _{i=0}^N\varvec{V}_{ij}^T\mathcal {L}(\varvec{U}_{ij})_x&= 2\sum _{i=0}^N\sum _{m=0}^N{\mathsf {Q}}_{im}\varvec{V}_{ij}^T\tilde{\varvec{F}}^{\mathrm {EC}}(\varvec{U}_{ij},\varvec{U}_{mj})\\&\quad -\left[ \varvec{V}^T\tilde{\varvec{F}}-\varvec{V}^T\tilde{\varvec{F}}^{\mathrm {EC}}\right] _{Nj}+\left[ \varvec{V}^T\tilde{\varvec{F}}+\varvec{V}^T\tilde{\varvec{F}}^{\mathrm {EC}}\right] _{0j}. \end{aligned} \end{aligned}$$

(A.11)

Again using $2{\mathsf {Q}}={\mathsf {Q}}-{\mathsf {Q}}^T+{\mathsf {B}}$ we have

$$\begin{aligned} \begin{aligned} \sum _{i=0}^N\varvec{V}_{ij}^T\mathcal {L}(\varvec{U}_{ij})_x=&\sum _{i=0}^N\sum _{m=0}^N{\mathsf {Q}}_{im}\varvec{V}_{ij}^T\tilde{\varvec{F}}^{\mathrm {EC}}(\varvec{U}_{ij},\varvec{U}_{mj})-\sum _{i=0}^N\sum _{m=0}^N{\mathsf {Q}}_{im}\varvec{V}_{ji}^T\tilde{\varvec{F}}^{\mathrm {EC}}(\varvec{U}_{mj},\varvec{U}_{ij})\\&+\varvec{V}_{Nj}^T\tilde{\varvec{F}}^{\mathrm {EC}}_{Nj}-\varvec{V}^T_{0j}\tilde{\varvec{F}}^{\mathrm {EC}}_{0j}. \end{aligned} \end{aligned}$$

(A.12)

Due to entropy conservation condition (1.24) and the consistency of the derivative matrix, i.e. $\mathsf {D}\varvec{1}=\varvec{0}~\left( \Leftrightarrow {\mathsf {Q}}\varvec{1}=\varvec{0}\right)$ we find

$$\begin{aligned} \begin{aligned} \sum _{i=0}^N\varvec{V}_{ij}^T\mathcal {L}(\varvec{U}_{ij})_x =&\sum _{i=0}^N\sum _{m=0}^N{\mathsf {Q}}_{im}\underbrace{\left( \left( \tilde{\varvec{F}}^{\mathrm {EC}}(\varvec{U}_{ij},\varvec{U}_{mj})\right) ^T\left( \varvec{V}_{ij}-\varvec{V}_{ji}\right) \right) }_{=\tilde{\varPsi }^f_{ij}-\tilde{\varPsi }^f_{mj}}\\&+\varvec{V}_{Nj}^T\tilde{\varvec{F}}^{\mathrm {EC}}_{Nj}-\varvec{V}_{0j}^T\tilde{\varvec{F}}^{\mathrm {EC}}_{0j},\\ =&\sum _{i=0}^N\tilde{\varPsi }^f_{ij}\underbrace{\sum _{m=0}^N{\mathsf {Q}}_{im}}_{=0}-\sum _{i=0}^N\sum _{m=0}^N\underbrace{{\mathsf {Q}}_{im}}_{{\mathsf {B}}_{im}-{\mathsf {Q}}_{mi}}\tilde{\varPsi }^f_{mj}+\varvec{V}_{Nj}^T\tilde{\varvec{F}}^{\mathrm {EC}}_{Nj}-\varvec{V}_{0j}^T\tilde{\varvec{F}}^{\mathrm {EC}}_{0j},\\ =&-\,\sum _{i=0}^N\sum _{m=0}^N{\mathsf {B}}_{im}\tilde{\varPsi }^f_{mj}+\sum _{m=0}^N\tilde{\varPsi }^f_{mj}\underbrace{\sum _{i=0}^N{\mathsf {Q}}_{mi}}_{=0}+\varvec{V}_{Nj}^T\tilde{\varvec{F}}^{\mathrm {EC}}_{Nj}-\varvec{V}_{0j}^T\tilde{\varvec{F}}^{\mathrm {EC}}_{0j},\\ =&\left( \varvec{V}_{Nj}^T\tilde{\varvec{F}}^{\mathrm {EC}}_{Nj}-\tilde{\varPsi }^f_{Nj}\right) -\left( \varvec{V}_{0j}^T\tilde{\varvec{F}}^{\mathrm {EC}}_{0j}-\tilde{\varPsi }^f_{0j}\right) . \end{aligned} \end{aligned}$$

(A.13)

And similar for $\sum \limits _{j=0}^N\varvec{V}_{ij}^T\mathcal {L}(\varvec{U}_{ij})_y$ we get

$$\begin{aligned} \sum _{j=0}^N\varvec{V}_{ij}^T\mathcal {L}(\varvec{U}_{ij})_y=\left( \varvec{V}_{iN}^T\tilde{\varvec{G}}^{\mathrm {EC}}_{iN}-\tilde{\varPsi }^g_{iN}\right) -\left( \varvec{V}_{i0}^T\tilde{\varvec{G}}^{\mathrm {EC}}_{i0}-\tilde{\varPsi }^g_{i0}\right) \end{aligned}$$

(A.14)

Both directions together yield

$$\begin{aligned} \begin{aligned} \underbrace{J\sum _{i,j=0}^N\omega _i\omega _j\left( S_{t}\right) _{ij}}_{\approx \int S_t\,\mathrm {d}E}=&-\,\sum _{j=0}^N\omega _j\left( \left( \varvec{V}_{Nj}^T\tilde{\varvec{F}}^{\mathrm {EC}}_{Nj}-\tilde{\varPsi }^f_{Nj}\right) -\left( \varvec{V}_{0j}^k\tilde{\varvec{F}}^{\mathrm {EC}}_{0j}-\tilde{\varPsi }^f_{0j}\right) \right) \\&-\sum _{i=0}^N\omega _i\left( \left( \varvec{V}_{iN}^T\tilde{\varvec{G}}^{\mathrm {EC}}_{iN}-\tilde{\varPsi }^g_{iN}\right) -\left( \varvec{V}_{i0}^T\tilde{\varvec{G}}^{\mathrm {EC}}_{i0}-\tilde{\varPsi }^g_{i0}\right) \right) , \end{aligned} \end{aligned}$$

(A.15)

which is precisely (2.6).

B Projection Operators for Discontinuous Galerkin Methods

The projection operators for DG methods are constructed with the Mortar Element Method by Kopriva [22].

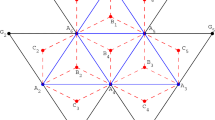
Here we assume two neighboring elements with a single coinciding interface as in Fig. 5. Let N, M denote the polynomial degrees of both elements with corresponding one-dimensional nodes $x_0^N,\ldots ,x_N^N$ and $x_0^M,\ldots ,x_M^M$ and integration weights $\omega _0^N,\ldots ,\omega _N^N$ and $\omega _0^M,\ldots ,\omega _M^M$. The corresponding norm matrices are defined as $\mathsf {M}_N={{\mathrm{diag}}}(\omega _0^N,\ldots ,\omega _N^N)$ and $\mathsf {M}_M={{\mathrm{diag}}}(\omega _0^M,\ldots ,\omega _M^M)$ and each element is equipped with a set of Lagrange basis functions $l_0^N,\ldots ,l_N^N$ and $l_0^M,\ldots ,l_M^M$.

As for the elements, the mortar also consists of a set of nodes, integration weights, norm matrix and Lagrange basis functions. Without lose of generality, we assume $N<M$. Therefore, the polynomial order on the mortar $N_{\varXi } = \max \{N,M\} = M$. So the mortar will simply copy the solution data from the element with the higher polynomial degree M because the nodal distributions are identical. Thus, the projection operator from the element to the mortar as well as back from the mortar to the element are simply the identity matrix of size M, i.e. ${\mathsf {P}}_{M2\varXi }={\mathsf {I}}^M$ and ${\mathsf {P}}_{\varXi 2M}={\mathsf {I}}^M$. Next, we briefly describe how to project the element of degree N to the mortar and back.

Step 1 (Projection from element of degree N to the mortar) Assume we have a discrete evaluated function $\varvec{f}=(f_0,\ldots ,f_N)^T$ with $f(x)=\sum _{i=0}^N\ell _i^N(x)f_i$. We want to project this function onto the mortar to obtain $\varvec{f}^{\varXi }=(f^{\varXi }_0,\ldots , f^{\varXi }_{M})^T$ with $f^{\varXi }(x)=\sum _{j=0}^{M}\ell _j^M(x) f^{\varXi }_j$. Note, that ${f}(x)\ne {f}^\varXi (x)$ for a polynomial of higher degree. In [22] the operator $P_{N2\varXi }$ is created by a $L_2$ projection on the mortar

$$\begin{aligned} \left\langle {f}, {\ell _j^M} \right\rangle _{L_2} = \left\langle {f^{\varXi }}, {\ell _j^M} \right\rangle _{L_2} \Leftrightarrow \sum _{i=0}^N\left\langle {\ell _i^N}, {\ell _j^M} \right\rangle _{L_2}f_i=\sum _{i=0}^M\left\langle {\ell _i^M}, {\ell _j^M} \right\rangle _{L_2}\ f^\varXi _i, \end{aligned}$$

(B.1)

for $j=0,\ldots ,M$. Here, the $L_2$ inner products are evaluated discretely using the appropriate norm matrices. The $L_2$ inner product on the left in (B.1) is evaluated exactly due to the high-order nature of the LGL quadrature and the assumption that $N<M$. Therefore, using M-LGL nodes and weights we have

$$\begin{aligned} \left\langle {\ell _i^N}, {\ell _j^M} \right\rangle _{L_2} = \left\langle {\ell _i^N}, {\ell _j^M} \right\rangle _{M} = \sum _{k=0}^M\omega _k^M\ell _i^N(x_k^M)\ell _j^M(x_k^M)=\sum _{k=0}^M\omega _k^M\ell _i^N(x_k^M)\delta _{jk}=\omega _j^M\ell _i^N(x_j^M), \end{aligned}$$

(B.2)

for $i=0,\ldots ,N$, $j=0,\ldots ,M$ and use the Kronecker delta property of the Lagrange basis. On the right side of (B.1) we evaluate an inner product of two polynomial basis functions of order M. Therefore, due to the exactness of the LGL quadrature, the $L_2$ inner product is approximated by an integration rule with mass lumping, e.g. [2],

$$\begin{aligned} \left\langle {\ell _i^M}, {\ell _j^M} \right\rangle _{L_2} \approx \left\langle {\ell _i^M}, {\ell _j^M} \right\rangle _{M} = \sum _{k=0}^M\omega _k^M\ell _i^M(x_k^M)\ell _j^M(x_k^M)=\sum _{k=0}^M\omega _k^M\delta _{ik} \delta _{jk} = \delta _{ij}\omega _j^M, \end{aligned}$$

(B.3)

for $i,j=0,\ldots ,M$. Next, we define interpolation operators

$$\begin{aligned} {[}{\mathsf {L}}_{N2\varXi }]_{ij}:= \ell _j^N(x_i^M), \end{aligned}$$

(B.4)

with $i=0,\ldots ,N$ and $j=0,\ldots ,M$ to rewrite (B.1) in a compact matrix-vector notation

$$\begin{aligned} \mathsf {M}_M{\mathsf {L}}_{N2\varXi } \varvec{f}=\mathsf {M}_M\varvec{f}^\varXi \Leftrightarrow \underbrace{{\mathsf {L}}_{N2\varXi }}_{:= {\mathsf {P}}_{N2\varXi }}\varvec{f}=\varvec{f}^\varXi . \end{aligned}$$

(B.5)

So the projection operator to move the solution from the element with N nodes onto the mortar is equivalent to an interpolation operator. However, this does not hold for projecting the solution from the mortar back to the element.

Step 2 (Projection from the mortar to element of degree N) To construct the operator ${\mathsf {P}}_{\varXi 2N}$ we consider the $L_2$ projection from the mortar back to an element with N nodes. Here, we assume a discrete evaluation of the solution on the mortar $\varvec{f}^\varXi =(f_0^\varXi ,\ldots ,f_M^\varXi )^T$ with $f^\varXi (x)=\sum _{i=0}^M \ell _i^M(x)f_i^\varXi$ and seek the solution on the element $\varvec{f}=( f_0,\ldots , f_N)^T$ with $f(x)=\sum _{i=0}^N \ell _i^N(x) f_i$. The $L_2$ projection back to the element is

$$\begin{aligned} \left\langle {f^{\varXi }}, {\ell _j^N} \right\rangle _{L_2}=\left\langle {f}, {\ell _j^N} \right\rangle _{L_2} \Leftrightarrow \sum _{i=0}^M \left\langle {\ell _i^M}, {\ell _j^N} \right\rangle _{L_2}f_i^\varXi =\sum _{i=0}^N\left\langle {\ell _i^N}, {\ell _j^N} \right\rangle _{L_2} f_i, \end{aligned}$$

(B.6)

for $j=0,\ldots ,N$. The $L_2$ inner product on the left in (B.6) is computed exactly using M-LGL points and the $L_2$ inner product on the right in (B.6) is approximated with mass lumping at N-LGL nodes. Thus, we obtain

$$\begin{aligned} \left\langle {\ell _i^M}, {\ell _j^N} \right\rangle _{L_2}=\left\langle {\ell _i^M}, {\ell _j^N} \right\rangle _{M}=\sum _{k=0}^M\omega _k^M \ell _i^M(x_k^M) \ell _j^N(x_k^M)=\omega _i^M \ell _j^N(x_i^M), \end{aligned}$$

(B.7)

where $i=0,\ldots ,M$, $j = 0,\ldots ,N$ and

$$\begin{aligned} \left\langle {\ell _i^N}, {\ell _j^N} \right\rangle _{L_2}\approx \left\langle {\ell _i^N}, {\ell _j^N} \right\rangle _{N}=\sum _{k=0}^N\omega _i^N \ell _i^N(x_k^N) \ell _j^N(x_k^N)=\delta _{ij}\omega _j^N, \end{aligned}$$

(B.8)

for $i,j=0,\ldots ,N$. Again, we write (B.6) in a compact matrix-vector notation which gives us

$$\begin{aligned} {\mathsf {L}}_{N2\varXi }^T\mathsf {M}_M\varvec{f}^\varXi =\mathsf {M}_N\varvec{f}. \end{aligned}$$

(B.9)

As ${\mathsf {L}}_{N2\varXi }={\mathsf {P}}_{N2\varXi }$ we obtain

$$\begin{aligned} \underbrace{\mathsf {M}_N^{-1}{\mathsf {P}}_{N2\varXi }^T\mathsf {M}_M}_{:={\mathsf {P}}_{\varXi 2N}}\varvec{f}^\varXi =\varvec{f}, \end{aligned}$$

(B.10)

where we introduce the projection operator (not interpolation operator) from the mortar back to the element with N nodes. With this approach we constructed projection operators satisfying the $\mathsf {M}$-compatibility condition (2.24), i.e.,

$$\begin{aligned} {\mathsf {P}}_{\varXi 2N}=\mathsf {M}_N^{-1}{\mathsf {P}}_{N2\varXi }^T\mathsf {M}_M\Leftrightarrow \mathsf {M}_N{\mathsf {P}}_{\varXi 2N}={\mathsf {P}}_{N2\varXi }^T\mathsf {M}_M. \end{aligned}$$

(B.11)

By combining the operators, we can construct projections which directly move the solution from one element to another (in some sense “hiding” the mortar) to be

$$\begin{aligned} \begin{aligned} {\mathsf {P}}_{N2M}&={\mathsf {P}}_{\varXi 2M}{\mathsf {P}}_{N2\varXi },\\ {\mathsf {P}}_{M2N}&={\mathsf {P}}_{\varXi 2N}{\mathsf {P}}_{M2\varXi }. \end{aligned} \end{aligned}$$

(B.12)

Note, that in this paper we only consider LGL-nodes for the approximating the $L_2$-projection. However, the approach in [22] is more general as it also considers Legendre Gauss nodes and the construction of projection operators on interfaces with hanging corners.

C Experimental Order of Convergence–Degree Preserving Element Based Finite Difference Operators

Besides Discontinuous Galerkin SBP operators, we analyze the convergence of degree preserving, element based finite difference operators (DPEBFD) operators. As described in [14] these operators are SBP operators by construction, for which our entropy stable discretization remains stable. The norm matrix of the DPEBFD operator integrates polynomials up to degree of $2p+1$ exactly, where p denotes the minimum polynomial degree of all elements. In comparison to SBP finite difference operators as in [9] these operators are element based, meaning that the number of nodes is fixed as for DG operators.

As we focus on elements with SBP operators of the same degree, we set all elements to be DPEBFD elements with degree p where $p=2,3$. To approximate the convergence order of the non-conforming discretization, we consider the same mesh refinement strategy as in Fig. 7 with element types A, B, B. These types are set up in the following way:

• Element A with 22 nodes in x- and y-direction,

• Element B with 24 nodes in x- and y-direction,

• Element C with 22 nodes in x- and y-direction.

This leads to a mesh considering h / p refinement. Here, we obtain the results in Tables 5, 6.

Table 5 Experimental order of convergence for DPEBFD operators with $p=2$

Table 6 Experimental order of convergence for DPEBFD operators with $p=3$

As documented in [14] we numerically verify an EOC of $p+1$. So when considering degree preserving SBP operators our entropy stable non-conforming method can handle h / p refinement and possesses full order. However when considering DG-operators we obtain a smaller $L_2$ error for a more coarse mesh. We do not claim that DPEBFD operators have the best error properties, but considering these operators is a possible cure for retaining a full order scheme. The development of optimal degree preserving SBP operators is left for future work.