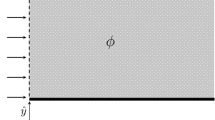
In this article we discuss singularly perturbed convection–diffusion equations in a channel in cases producing parabolic boundary layers. It has been shown that one can improve the numerical resolution of singularly perturbed problems involving boundary layers, by incorporating the structure of the boundary layers into the finite element spaces, when this structure is available; see e.g. [Cheng, W. and Temam, R. (2002). Comput. Fluid. V.31, 453–466; Jung, C. (2005). Numer. Meth. Partial Differ. Eq. V.21, 623–648]. This approach is developed in this article for a convection–diffusion equation. Using an analytical approach, we first derive an approximate (simplified) form of the parabolic boundary layers (elements) for our problem; we then develop new numerical schemes using these boundary layer elements. The results are performed for the perturbation parameter ε in the range 10−1–10−15 whereas the discretization mesh is in the range of order 1/10–1/100 in the x-direction and of order 1/10–1/30 in the y-direction. Indications on various extensions of this work are briefly described at the end of the Introduction.
Similar content being viewed by others
References
Cheng W., Temam R. (2002). Numerical approximation of one-dimensional stationary diffusion equations with boundary layers. Comput. Fluid. V.31, 453–466
Cheng W., Temam R., Wang X. (2000). New approximation algorithms for a class of partial differential equations displaying boundary layer behavior. Meth. Appl. Anal. V.7(2): 363–390
Ciarlet P. G. (1978). The Finite Element Method for Elliptic Problems. North-Holland, New York.
Eckhaus W. (1972). Boundary layers in linear elliptic singular perturbations. SIAM Rev. V.14, 225–270
Eckhaus W., and De Jager E.M. (1966). Asymptotic solutions of singular perturbation problems for linear differential equations of elliptic type. Arch. Rational Mech. Anal. V.23, 26–86
Evans L.C. (1998). Partial Differential Equations. AMS, Providence Rhode Island.
Gilbarg D., Trudinger N.S. (1998). Elliptic Partial Differential Equations of Second Order. Springer-Verlag, New York
Goering H., Felgenhauer A., Lube G., Roose H.-G., Tobiska L. (1983). Singularly Perturbed Differential Equations. Akademie-Verlag, Berlin
Holmes M.H. (1995). Introduction to Perturbation Methods. Springer-Verlag, New York
Jung C. (2005). Numerical approximation of two-dimensional convection-diffusion equations with boundary layers. Numer. Meth. Partial Diff. Eq. V.21(3): 623–648
Jung C. Numerical approximation of convection-diffusion equations in a channel using boundary layer elements. Appl. Numer. Math. To appear.
Jung C., Temam R. (2005). Numerical approximation of two-dimensional convection-diffusion equations with multiple boundary layers. Int. J. Numer. Analy. Modeling. V.2(4): 367–408
Jung, C., and Temam, R. Double-gyre problems and singular perturbation with numerical applications. In preparation.
Knaub K.R., O’Malley R.E. (2004). The motion of internal layers in singularly perturbed advection–diffusion–reaction equations. Stud. Appl. Math. V.112(1): 1–15
Lions J.L. (1973). Perturbations singulières dans les problèmes aux limites et en contrôle optimal. (French) Lecture Notes in Mathematics, Vol. 323. Springer-Verlag, Berlin-New York
Larsson S., Thomée V. (2003). Partial Differential Equations with Numerical Methods. Springer-Verlag, Berlin
O’Malley R.E. (1977). Singular perturbation Analysis for Ordinary Differential Equations. Communications of the Mathematical Institute, Rijksuniversiteit Utrecht, Rijksuniversiteit Utrecht, Mathematical Institute, Utrecht
O’Malley R.E. (1991). Singular Perturbation Methods for Ordinary Differential Equations. Springer-Verlag, New York
O’Malley R.E. (2001). Naive singular perturbation theory. Special issue in memory of Richard Weiss. Math. Models. Meth. Appl. Sci. V.11(1): 119–131
Roos H.-G., Stynes M., Tobiska L. (1996). Numerical Methods for Singularly Perturbed Differential Equations. Springer-Verlag, Berlin
Schultz M.H. (1973). Spline Analysis. Prentice-Hall, Inc., Englewood Cliffs, NJ
Stynes M. (2005). Steady-state convection–diffusion problems Acta Numerica. Cambridge University Press, Cambridge, pp. 445–508.
Shih S., Kellogg R.B. (1987). Asymptotic analysis of a singular perturbation problem. SIAM J. Math. Anal. V.18, 1467–1511
Temam, R. (1997). Infinite dimensional dynamical systems in mechanics and physics, Appl. Math. Sci. Ser. Vol. 68. Springer-Verlag, New-York.
Vishik M.I., Lyusternik L.A. (1957). Regular degeneration and boundary layer for linear differential equations with small parameter. Uspekki Mat. Nauk. 12, 3–122
Vretblad A. (2003). Fourier Analysis and Its Applications. Springer-Verlag, New-York
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to David Gottlieb on his 60th birthday.
Rights and permissions
About this article
Cite this article
Jung, CY., Temam, R. On Parabolic Boundary Layers for Convection–Diffusion Equations in a Channel: Analysis and Numerical Applications. J Sci Comput 28, 361–410 (2006). https://doi.org/10.1007/s10915-006-9086-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-006-9086-8
Keywords
- Boundary layers
- parabolic boundary layers
- finite elements
- singularly perturbed problem
- convection–diffusion