Modelling linear reactions in inhomogeneous catalytic systems

Abstract

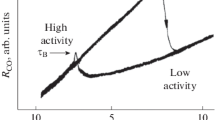
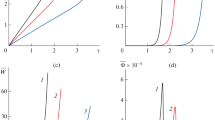
The kinetics of linear chemical reactions in an inhomogeneous medium is modeled as an evolutionary system characterized by a fractional derivative. The corresponding mathematical model depending on one nonlocal parameter $0< \alpha <1$ is proposed. Reactions with one degree of freedom are analyzed. Solutions of the corresponding kinetic equations are shown to depend on the nonlocality parameter $\alpha$. The concept of the critical moment of time is introduced, and the dependence of its value on the value of the relaxation coefficient is determined.

Appendix

The left Riemann–Liouville fractional derivative

$$\begin{aligned} { }_a^{RL}{D_{t+}}^\alpha f(t)=\frac{1}{{\varGamma }(n-\alpha )}\left( {\frac{d}{dt}} \right)^{n}\int \limits _a^t {\frac{f(\tau )d\tau }{(t-\tau )^{1+\alpha -n}}.} \end{aligned}$$

(30)

The right fractional derivative

$$\begin{aligned} { }_b^{RL}{D_{t-}}^\alpha f(t)=\frac{1}{{\varGamma }(n-\alpha )}\left( {-\frac{d}{dt}} \right)^{n}\int \limits _t^b {\frac{f(\tau )d\tau }{(\tau -t)^{1+\alpha -n}} ,} \end{aligned}$$

(31)

where $n=|\alpha |+1$ and $\alpha >0$.

Unfortunately, the Riemann–Liouville fractional derivative of the constant function is non-zero. This is not convenient when analysing, e.g., the asymptotic and other states. To escape this inconvenience, the corresponding Caputo fractional derivatives are defined as follows:

• the left Caputo fractional derivative

  $$\begin{aligned} { }_aD_{t+}^\alpha f(t)=\frac{1}{{\varGamma }(n-\alpha )}\int \limits _a^t {\frac{d\tau }{(t-\tau )^{1+\alpha -n}}\left( {\frac{df(\tau )}{d\tau }} \right)^{n}} \end{aligned}$$

  (32)

• the right Caputo fractional derivative

  $$\begin{aligned} { }_bD_{t-}^\alpha f(t)=\frac{1}{{\varGamma }(n-\alpha )}\int \limits _t^b {\frac{d\tau }{(\tau -t)^{1+\alpha -n}}\left( {\frac{df(\tau )}{d\tau }} \right)^{n},} \end{aligned}$$

  (33)

where $\alpha$ represents the order of the derivative: $n-1<\alpha <n$ and $\alpha >0$.

The relationship between the Riemann–Liouville and the Caputo fractional derivatives is $(0<\alpha <1)$:

$$\begin{aligned} { }_aD_{t+}^\alpha f(t)&= { }_a^{RL}{D_{t+}}^\alpha f(t)-\frac{1}{{\varGamma }(1-\alpha )}\frac{f(a)}{(t-a)^{\alpha }},\end{aligned}$$

(34)

$$\begin{aligned} { }_bD_{t-}^\alpha f(t)&= { }_b^{RL}{D_{t-}}^\alpha f(t)-\frac{1}{{\varGamma }(1-\alpha )}\frac{f(b)}{(b-t)^{\alpha }}. \end{aligned}$$

(35)

Thus, e.g., the left Riemann–Liouville fractional derivative of the constant function $C$ equals $C/\left| {{\varGamma }(1-\alpha )(t-a)^{\alpha }} \right|$, whereas the left Caputo fractional derivative is equal to zero. On the other hand, many properties of the Caputo fractional derivatives are the same as those of the Riemann–Liouville fractional derivative when $f(a)=f(b)=0$:

$$\begin{aligned}&{ }_aD_{t+}^{-\alpha } f(t)={ }_aI_{t+}^\alpha f(t),\quad { }_bD_{t-}^{-\alpha } f(t)={ }_bI_{t-}^\alpha f(t),\quad \quad \alpha >0\end{aligned}$$

(36)

$$\begin{aligned}&{ }_aI_{t+}^\alpha f(t)=\frac{1}{{\varGamma }(\alpha )}\int \limits _a^t {\frac{f(\tau )d\tau }{(t-\tau )^{1-\alpha }}} -,\quad \quad t>a,\end{aligned}$$

(37)

$$\begin{aligned}&{ }_bI_{t-}^\alpha f(t)=\frac{1}{{\varGamma }(\alpha )}\int \limits _t^b {\frac{f(\tau )d\tau }{(\tau -t)^{1-\alpha }}} -,\quad \quad t<b,\end{aligned}$$

(38)

$$\begin{aligned}&{ }_aD_{t+}^\alpha f(t)={ }_aI_{t+}^{-\alpha } f(t),\quad \quad { }_bD_{t-}^\alpha f(t)={ }_bI_{t-}^{-\alpha } f(t),\quad \quad \alpha >0\end{aligned}$$

(39)

$$\begin{aligned}&{ }_aD_{t+}^\alpha { }_aD_{t+}^\beta f(t)={ }_aD_{t+}^\beta { }_aD_{t+}^\alpha f(t)={ }_aD_{t+}^{\alpha +\beta } f(t),\end{aligned}$$

(40)

$$\begin{aligned}&{ }_aI_{t+}^\alpha { }_aI_{t+}^\beta f(t)={ }_aI_{t+}^\beta { }_aI_{t+}^\alpha f(t)={ }_aI_{t+}^{\alpha +\beta } f(t), \end{aligned}$$

(41)

The analogue of the Taylor expansion is valid here:

$$\begin{aligned} f(t)=\sum _{i=0}^{n-1} {\frac{{ }_aD_{t+}^{\alpha +j} f(0)}{{\varGamma }(1+\alpha +j)}} t^{\alpha +j}+R_n (t),\quad \quad n=\left[ {\text{ Re} \alpha } \right]+1, \end{aligned}$$

(42)

where $R_n (t) ={ }_aI_{t+}^{\alpha +j} { }_aD_{t+}^{\alpha +j} f(t)$.

As an example, let us consider the derivatives of some functions:

$$\begin{aligned}&{ }_{-\infty }D_{t+}^\alpha \sin \lambda t=\lambda ^{\alpha }\sin \left( {\lambda t+\frac{\pi \alpha }{2}} \right),\end{aligned}$$

(43)

$$\begin{aligned}&{ }_{-\infty }D_{t+}^\alpha \cos \lambda t=\lambda ^{\alpha }\cos \left( {\lambda t+\frac{\pi \alpha }{2}} \right), \end{aligned}$$

(44)

where $\lambda >0, \quad \alpha >-1.$ When $\alpha \le -1,$we have to use the property (39):

$$\begin{aligned} { }_{-\infty }D_{t+}^\alpha e^{\lambda t+\mu }=\lambda ^{\alpha }e^{\lambda t+\mu },\quad \quad \text{ Re} \lambda >0. \end{aligned}$$

(45)

Some special functions, e.g., the Mittag-Leffler function

$$\begin{aligned} E_{\alpha ,\beta } (z)=\sum _{n=0}^\infty {\frac{z^{n}}{{\varGamma }(\alpha n+\beta )}} \end{aligned}$$

(46)

and the generalized exponential function

$$\begin{aligned} 1+E_\alpha ^z =1+\sum _{n=0}^\infty {\frac{z^{n+\alpha }}{{\varGamma }(1+\alpha +n)}} , \end{aligned}$$

(47)

naturally appear and are widely used in fractional calculus.

In this paper, the fractional Caputo derivative ${ }_{t_0 }D_{t+}^\alpha =\frac{d^{\alpha }}{dt^{\alpha }}$ is used.