Cutting circles and polygons from area-minimizing rectangles

Abstract

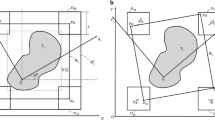
A set of circles, rectangles, and convex polygons are to be cut from rectangular design plates to be produced, or from a set of stocked rectangles of known geometric dimensions. The objective is to minimize the area of the design rectangles. The design plates are subject to lower and upper bounds of their widths and lengths. The objects are free of any orientation restrictions. If all nested objects fit into one design or stocked plate the problem is formulated and solved as a nonconvex nonlinear programming problem. If the number of objects cannot be cut from a single plate, additional integer variables are needed to represent the allocation problem leading to a nonconvex mixed integer nonlinear optimization problem. This is the first time that circles and arbitrary convex polygons are treated simultaneously in this context. We present exact mathematical programming solutions to both the design and allocation problem. For small number of objects to be cut we compute globally optimal solutions. One key idea in the developed NLP and MINLP models is to use separating hyperplanes to ensure that rectangles and polygons do not overlap with each other or with the circles. Another important idea used when dealing with several resource rectangles is to develop a model formulation which connects the binary variables only to the variables representing the center of the circles or the vertices of the polytopes but not to the non-overlap or shape constraints. We support the solution process by symmetry breaking constraints. In addition we compute lower bounds, which are constructed by a relaxed model in which each polygon is replaced by the largest circle fitting into that polygon. We have successfully applied several solution techniques to solve this problem among them the Branch&Reduce Optimization Navigator (BARON) and the LindoGlobal solver called from GAMS, and, as described in Rebennack et al. [21], a column enumeration approach in which the columns represent the assignments. Good feasible solutions are computed within seconds or minutes usually during preprocessing. In most cases they turn out to be globally optimal. For up to 10 circles, we prove global optimality up to a gap of the order of 10⁻⁸ in short time. Cases with a modest number of objects, for instance, 6 circles and 3 rectangles, are also solved in short time to global optimality. For test instances involving non-rectangular polygons it is difficult to obtain small gaps. In such cases we are content to obtain gaps of the order of 10%.