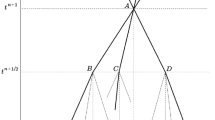
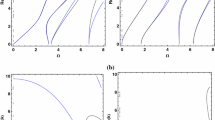
The setting of boundary conditions on curvilinear walls in application to the multidimensional nodal method of characteristics is discussed, which is based on splitting the initial system of equations into a number of one-dimensional subsystems along the coordinate directions. For the boundary points located on curvilinear impermeable surfaces, a calculation method based on the procedure of fictitious nodes is suggested, with the use of which a number of test problems with self-similar solutions have been calculated.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. S. Surov, Heterogeneous media. Hyperbolic models and methods of calculation, Proc. XXI Int. Conf. Comp. Meth. Sovr. Prikl. Program Syst., Izd. MAI, Moscow (2019), pp. 350–352.
V. S. Surov, On calculation of flows of heterogeneous media in a body-force field, J. Eng. Phys. Thermophys., 93, No. 4, 878–884 (2020).
P. Rouch, Computational Hydrodynamics [Russian translation], Mir, Moscow (1980).
D. A. Anderson, J. C. Tannehill, and R. H. Pletcher, Computational Fluid Mechanics and Heat Transfer [Russian translation], Mir, Moscow (1990).
S. K. Godunov, A. V. Zabrodin, M. Ya. Ivanov, A. N. Kraiko, and G. P. Prokopov, Numerical Solution of Multidimensional Problems of Gas Dynamics [in Russian], Nauka, Moscow (1976).
Yu. A. Grishin, V. A. Zenkin, and R. N. Khmelev, Boundary conditions for numerical calculation of gas exchange in piston engines, J. Eng. Phys. Thermophys., 90, No. 4, 965–970 (2017).
V. S. Surov, On hyperbolization of a number of continuum mechanics models, J. Eng. Phys. Thermophys., 92, No. 5, 1302–1317 (2019).
V. S. Surov, On a variant of the method of characteristics for calculating one-velocity flows of a multicomponent mixture, J. Eng. Phys. Thermophys., 83, No. 2, 366–372 (2010).
V. S. Surov, On a method of approximate solution of the Riemann problem for a one-velocity flow of a multicomponent mixture, J. Eng. Phys. Thermophys., 83, No. 2, 373–379 (2010).
A. G. Kulikovskii, N. V. Pogorelov, and A. Yu. Semenov, Mathematical Problems of Numerical Solution of Hyperbolic Systems of Equations [in Russian], Fizmatlit, Moscow (2012).
E. F. Toro, Riemann solvers with evolved initial condition, Int. J. Numer. Methods Fluids, 52, 433–453 (2006).
V. S. Surov, Shock adiabat of a one-velocity heterogeneous medium, J. Eng. Phys. Thermophys., 79, No. 5, 886–892 (2006).
V. S. Surov, Certain self-similar problems of flows of a one-velocity heterogeneous medium, J. Eng. Phys. Thermophys., 80, No. 6, 1237–1246 (2007).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 94, No. 3, pp. 715–721, May–June, 2021.
Rights and permissions
About this article
Cite this article
Surov, V.S. On the Problem of Boundary Conditions in the Multidimensional Nodal Method of Characteristics. J Eng Phys Thermophy 94, 695–701 (2021). https://doi.org/10.1007/s10891-021-02346-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-021-02346-1