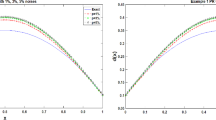
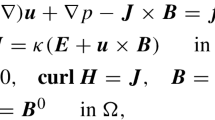With the use of the integral heat balance method based on the introduction of the temperature perturbation field and additional boundary conditions, we consider a method for finding analytical solutions of boundary-value problems of nonstationary heat conduction that permits obtaining, for a series of problems, solutions with a given degree of accuracy throughout the range of variation of the Fourier number. Solutions have a simple form of exponential algebraic polynomials, which makes it possible to investigate the heat transfer in the fields of isothermal lines, as well as analyze the time distributions of velocities of motion of isotherms.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. A. Kudinov, É. M. Kartashov, and V. V. Kalashnikov, Analytical Solutions of the Problems of Heat- and Mass Transfer and Thermal Elasticity for Multilayer Structures: Manual for Higher Educational Establishments [in Russian], Vysshaya Shkola, Moscow (2005).
V. A. Kudinov, Method of coordinate functions in nonstationary heat-conduction problems, Izv. Ross. Akad. Nauk, Énergetika, No. 3, 84–107 (2004).
T. Goodmen, Application of integral methods in nonlinear problems of nonstationary heat transfer, in: Heat Transfer Problems [Russian translation], Atomizdat, Moscow (1967), pp. 41–96.
N. M. Belyaev and A. A. Ryadno, Methods of Nonstationary Heat Conduction: Manual for Higher Educational Establishments [in Russian], Vysshaya Shkola, Moscow (1978).
Yu. S. Postol’nik, Methods of averaging functional corrections in heat-conduction problems, in: Heat- and Mass Transfer, Vol. 8, Minsk (1972), pp. 23–29.
M. A. Biot, Variational Principles in Heat Transfer [Russian translation], Énergiya, Moscow (1975).
A. I. Veinik, Approximate Calculation of Heat-Conduction Processes [in Russian], Gosénergoizdat, Moscow–Leningrad (1959).
V. A. Kudinov, B. V. Averin, E. V. Stefanyuk, and S. A. Nazarenko, Analytical solutions of heat-conduction problems with a variable initial condition on the basis of determining the temperature perturbation front, Inzh.-Fiz. Zh., 80, No. 3, 27–35 (2007).
V. A. Kudinov, B. V. Averin, and E. V. Stefanyuk, Solutions of heat-conduction problems under time-variable boundary conditions on the basis of determining the temperature perturbation front, Izv. Ross. Akad. Nauk, Énergetika, No. 1, 55–68 (2007).
É . M. Kartashov, Analytical Methods in the Theory of Heat Conduction of Solids [in Russian], Vysshaya Shkola, Moscow (2001).
A. V. Luikov, Theory of Heat Conduction [in Russian], Vysshaya Shkola, Moscow (1967).
N. M. Tsirel’man, Direct and Inverse Heat and Mass Transfer Problems [in Russian], Énergoatomizdat, Moscow (2005).
V. A. Kudinov, B. V. Averin, and E. V. Stefanyuk, Heat Conductivity and Thermoelasticity of Multilayer Structures: Manual for Higher Educational Establishments [in Russian], Vysshaya Shkola, Moscow (2008).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 82, No. 3, pp. 540–558, May–June, 2009.
Rights and permissions
About this article
Cite this article
Kudinov, V.A., Stefanyuk, E.V. Analytical solution method for heat conduction problems based on the introduction of the temperature perturbation front and additional boundary conditions. J Eng Phys Thermophy 82, 537–555 (2009). https://doi.org/10.1007/s10891-009-0223-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-009-0223-8