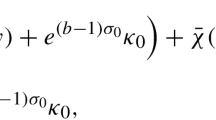Meanders, Zero Numbers and the Cell Structure of Sturm Global Attractors

Abstract

We study global attractors $\mathcal {A}=\mathcal {A}_f$ of semiflows generated by semilinear partial parabolic differential equations of the form $u_t = u_{xx} + f(x,u,u_x), 0<x<1$, satisfying Neumann boundary conditions. The equilibria $v\in \mathcal {E}\subset \mathcal {A}$ of the semiflow are the stationary solutions of the PDE, hence they are solutions of the corresponding second order ODE boundary value problem. Assuming hyperbolicity of all equilibria, the dynamic decomposition of $\mathcal {A}$ into unstable manifolds of equilibria provides a geometric and topological characterization of Sturm global attractors $\mathcal {A}$ as finite regular signed CW-complexes, the Sturm complexes, with cells given by the unstable manifolds of equilibria. Concurrently, the permutation $\sigma =\sigma _f$ derived from the ODE boundary value problem by ordering the equilibria according to their values at the boundaries $x=0,1$, respectively, completely determines the Sturm global attractor $\mathcal {A}$. Equivalently, we use a planar curve, the meander $\mathcal {M}=\mathcal {M}_f$, associated to the the ODE boundary value problem by shooting. In the previous paper (Fiedler and Rocha in J Dyn Differ Equ, 2020. https://doi.org/10.1007/s10884-020-09836-5), we set up to determine the boundary neighbors of any specific unstable equilibrium $\mathcal {O}$, based exclusively on the information on the corresponding signed hemisphere complex. In addition, a certain minimax property of the boundary neighbors was established. In the signed hemisphere decomposition of the cell boundary of $\mathcal {O}$, this property identifies the equilibria which are closest to, or most distant from, $\mathcal {O}$ at the boundaries $x=0,1$, in each hemisphere. The main objective of the present paper is to derive this minimax property directly from the Sturm permutation $\sigma$, or equivalently from the Sturm meander $\mathcal {M}$, based on the Sturm nodal properties of the solutions of the ODE boundary value problem. This minimax result simplifies the task of identifying the equilibria on the cell boundary of each unstable equilibrium, directly from the Sturm meander $\mathcal {M}$. We emphasize the local aspect of this result by an example for which the identification of the equilibria is obtained from the knowledge of only a segment of the Sturm meander $\mathcal {M}$.

Appendices

Appendix: Nonlinear Sturm-Liouville Property

In this Appendix we review and prove the nonlinear Sturm-Liouville property (NSL for short) in our meander setting. Let $v_j=h_0(j), v_k=h_0(k)$ denote two equilibria with $j<k$. Then, the NSL property corresponds to the relation (2.5) between zero numbers, Morse indices and crossing numbers, which we now repeat for convenience. The claim is that the zero number $z_{j\,k}:=z(v_k-v_j)$ is given by ( [32, Proposition 3])

$$\begin{aligned} z(v_k-v_j) = {\left\{ \begin{array}{ll} \ i(v_j) + c(j,k;j), &{} \text { if } Q\mathcal {M}_{j\,j+1} \text { is odd } \,; \\ \\ \ i(v_j) - 1 + c(j,k;j), &{} \text { if } Q\mathcal {M}_{j\,j+1} \text { is even } \,, \end{array}\right. } \end{aligned}$$

(5.1)

Here $Q\mathcal {M}_{j\,j+1}$ denotes the quadrant with respect to j of the arc segment of $\mathcal {M}$ between the intersection points j and $j+1$.

As in Sect. 2, c(j, k; j) denotes the net signed clockwise crossings of the oriented meander segment $\mathcal {M}_{j\,k}$ from equilibrium crossing j to k through the vertical line of j, ignoring that first crossing. See (2.3), (2.4).

Our proof of the NSL property (5.1) is based on zeros and winding numbers associated to the solutions $v=v(x,a)$ of the initial value second order ODE problem

$$\begin{aligned} 0=v_{xx}+f(x,v,v_x) \quad , \quad v(0,a)=a , \quad v_x(0,a)=0 . \end{aligned}$$

(5.2)

The equilibrium boundary value problem (1.2) is related to this ODE by the shooting condition $v_x(x,a)=0$ at the right boundary $x=1$. Let $a_j:=v_j(0),\ a_k:=v_k(0)$ denote the initial values at $x=0$ of the equilibria $v_j, v_k\in \mathcal {E}$, i.e.

$$\begin{aligned} v(\cdot ,a_j)=v_j(\cdot ) \,, \qquad v(\cdot ,a_k)=v_k(\cdot ) \,. \end{aligned}$$

(5.3)

Then the segment $\mathcal {M}_{j\,k}$ of the meander $\mathcal {M}$, from the intersection point j to the intersection point k, is given by the planar curve

$$\begin{aligned} a\mapsto (v(1,a),v_x(1,a))\in \mathbb {R}^2 \,, \qquad a_j \le a \le a_k \end{aligned}$$

(5.4)

of boundary values at the shooting boundary $x=1$. Note how the shooting condition $v_x(1,a)=0$ is actually satisfied, precisely, at the equilibrium intersections of the meander $\mathcal {M}$ with the horizontal axis $v_x=0$ in the $(v,v_x)$-plane.

For $a_j<a\le a_k$ , let

$$\begin{aligned} w=w(x,a):=(v(x,a)-v_j(x))/(a-a_j) \end{aligned}$$

(5.5)

denote the scaled difference between the two solutions $v,v_j$ of (5.2). Note that $w=w(x,a)$ solves a linear second order ODE initial value problem

$$\begin{aligned} 0 = w_{xx}+q_1(x,a)w_x+q_0(x,a)w \,, \qquad w(0,a)=1, \quad w_x(0,a)=0 \,. \end{aligned}$$

(5.6)

Indeed, the coefficients $q_0, q_1$ depend on $v, v_j$ and are given explicitly as

$$\begin{aligned} \begin{aligned} q_0(x,a) =&\int _0^1 \partial _u f(x,r(x,a,\mu ),r_x(x,a,\mu )) \ d\mu \,, \\ q_1(x,a) =&\int _0^1 \partial _p f(x,r(x,a,\mu ),r_x(x,a,\mu )) \ d\mu \,, \end{aligned} \end{aligned}$$

(5.7)

with $r(x,a,\mu ) = \mu v(x,a) + (1-\mu ) v_j(x)$, by the Fundamental Theorem of Calculus.

To extend the above construction (5.5)–(5.7), down to $a=a_j$ , let

$$\begin{aligned} q_0(x,a_j) := \partial _u f(x,v_j(x),v_{j\,x}(x)) \,, \qquad q_1(x,a_j) := \partial _p f(x,v_j(x),v_{j\,x}(x)) \,. \end{aligned}$$

(5.8)

Then $f\in C^1$ implies continuity of $q_0, q_1$ , and therefore continuity of $w,w_x\in C^1$, in the closed rectangle

$$\begin{aligned} (x,a)\in {\mathcal {R}}:=[0,1]\times [a_j,a_k]\,. \end{aligned}$$

(5.9)

The initial condition $w(0,a)=1$ of the linear equation (5.6) implies $(w(x,a),w_x(x,a))\ne (0,0)$ on ${\mathcal {R}}$. We can therefore introduce (clockwise!) polar coordinates, according to the Prüfer transformation

$$\begin{aligned} w=\rho \cos \vartheta \,, \quad w_x=-\rho \sin \vartheta \, \end{aligned}$$

(5.10)

and obtain

$$\begin{aligned} \begin{aligned} \rho _x =&- \rho \left( q_1(x,a) \sin ^2\vartheta +(1-q_0(x,a)) \sin \vartheta \cos \vartheta \right) \\ \\ \vartheta _x =&\sin ^2\vartheta - q_1(x,a) \sin \vartheta \cos \vartheta + q_0(x,a) \cos ^2\vartheta \,. \end{aligned} \end{aligned}$$

(5.11)

Note how the initial conditions $w(0,a)=1,\ w_x(0,a)=0$ imply $\rho =1,\ \vartheta =0$ at $x=0$. The first equation of (5.11) then implies $\rho >0$ on the rectangle ${\mathcal {R}}$. In particular all zeros of $x\mapsto w(x,a)$ are simple, for any fixed a. The second equation implies $\vartheta _x>0$ for $\cos \vartheta =0$, i.e. whenever $w=0$, alias $\vartheta =\frac{1}{2}{\pi }\,(\mathrm {mod}\,\pi )$. Hence the total number of zeros of the solutions $x\mapsto w=w(x,a)$ relates to the winding of $x\mapsto \vartheta =\vartheta (x,a)$.

Fig. 7

Illustration of the rectangle ${\mathcal {R}}:=[0,1]\times [a_j,a_k]$. On each side of ${\mathcal {R}}$ is indicated the total winding of $\vartheta$ along the corresponding side. On the top side, the two values correspond to the alternative: $\mathcal {M}_{j\,j+1}$ is in an odd/even quadrant with respect to j

We can now outline the remaining proof of the NSL property (5.1) as follows. We first note that the winding number of

$$\begin{aligned} \vartheta \,(\mathrm {mod}\,2\pi ): \quad \partial {\mathcal {R}} \rightarrow S^1 \end{aligned}$$

(5.12)

is zero, along the boundary $\partial {\mathcal {R}}$ of the rectangle ${\mathcal {R}}$ in (5.9). Indeed, the map extends to all of ${\mathcal {R}}$, continuously, and hence is contractible, i.e. of winding number zero. In Lemma 5.1 we relate the winding along the right boundary $a=a_k,\ 0\le x\le 1$ of ${\mathcal {R}}$ to the zero number $z(v_k-v_j)$ in claim (5.1). In Lemma 5.2 we relate the winding along the left boundary $a=a_j,\ 0\le x\le 1$ of ${\mathcal {R}}$ to the Morse index $i(v_j)$ in claim (5.1). In Lemma 5.3 we relate the winding along the upper boundary $x=1,\ a_j\le a\le a_k$ of ${\mathcal {R}}$ to the crossing number c(j, k; j) in claim (5.1). Since $\vartheta =0$ is constant along the lower boundary $x=0,\ a_j\le a\le a_k$ , and since the total winding number is zero, this reduces the proof of the NSL property (5.1) to the three Lemmata 5.1–5.3.

Lemma 5.1

The zero number $z(v_k-v_j)$ is given by

$$\begin{aligned} z(v_k-v_j)=z(w(\cdot ,a_k))=\vartheta (1,a_k)/\pi \,. \end{aligned}$$

(5.13)

Proof

Fix $a=a_k$. We recall that all zeros of $w(\cdot ,a_k)$ are simple. They correspond to clockwise crossings of $(w,w_x)$ through the vertical $w_x$-axis or, equivalently, to simple zeros of $\vartheta -\tfrac{1}{2}\pi \,(\mathrm {mod}\,\pi )$ with positive slope $\vartheta _x>0$ . The Neumann boundary condition $v_{k\,x}=v_{j\,x}=0$ at $x=1$ implies $w_x=0$ and hence $\vartheta \equiv 0\,(\mathrm {mod}\,\pi )$ there. This proves the lemma. $\square$

Lemma 5.2

The Morse index $i(v_j)$, i.e. the unstable dimension of the equilibrium $v_j$, satisfies

$$\begin{aligned} i(v_j) = \lfloor \vartheta (1,a_j)/\pi \rfloor +1\,. \end{aligned}$$

(5.14)

Here $\lfloor \cdot \rfloor$ denotes the integer valued floor function.

Proof

See for example [31, Theorem 2].

Comparing (5.2) with (5.5), (5.6), (5.8), we first note that $w=v_a$ is the partial derivative of $v=v(\cdot ,a)$ with respect to a, at $a=a_j$. In particular, $(w(1,a_j),w_x(1,a_j))$ is the tangent of the meander segment $\mathcal {M}_{j\,j+1}$ at j, at (clockwise) angle $\vartheta (1,a_j)\,(\mathrm {mod}\,2\pi )$ from the horizontal axis; see (5.10). Since the equilibrium $v_j$ is assumed to be hyperbolic, $\vartheta (1,a_j) \ne 0 \,(\mathrm {mod}\,\pi )$. In particular the meander crosses the horizontal axis transversely at the intersection j. More precisely, the (clockwise) tangent angle $\vartheta (1,a_j)$ has to point above the horizontal axis, for odd j (alias even $i(v_j)$), and below for even j (alias odd $i(v_j)$), alternatingly:

$$\begin{aligned} \vartheta (1,a_j) \,(\mathrm {mod}\,2\pi )\in {\left\{ \begin{array}{ll} (0,\pi )\,,&{} \text { for odd }i(v_j)\,; \\ (\pi ,2\pi )\,,&{} \text { for even }i(v_j)\,. \end{array}\right. } \end{aligned}$$

(5.15)

Next, consider the simple eigenvalues $\lambda _m$ , i.e.

$$\begin{aligned} \lambda _0> \dots> \lambda _{i(v_j)-1}> 0> \lambda _{i(v_j)} > \dots \,, \end{aligned}$$

(5.16)

of the linearization

$$\begin{aligned} \lambda {\tilde{v}}={\tilde{v}}_{xx}+q_1(x,a_j){\tilde{v}}_x+q_0(x,a_j){\tilde{v}} \,, \quad {\tilde{v}}(0)=1, \quad {\tilde{v}}_x(0)={\tilde{v}}_x(1)=0 \end{aligned}$$

(5.17)

at $v_j$. By classical Sturm-Liouville theory, e.g. as in [6], the eigenfunction ${\tilde{v}} = {\tilde{v}}_m$ of $\lambda =\lambda _m$ possesses m simple zeros. Moreover, w solves (5.17) with $\lambda =0$, but violates the Neumann boundary condition at $x=1$. Therefore Sturm-Liouville comparison with (5.16) implies

$$\begin{aligned} i(v_j)-1 \le z(w) \le i(v_j)\,. \end{aligned}$$

(5.18)

Translating zeros of w to zeros of $\vartheta - \tfrac{1}{2} \pi \,(\mathrm {mod}\,\pi )$, as in the proof of Lemma 5.1, we obtain

$$\begin{aligned} (i(v_j)-1)\pi< \vartheta (1,a_j)- \pi /2 < (i(v_j)+1)\pi \,. \end{aligned}$$

(5.19)

Combined with (5.15), this implies

$$\begin{aligned} (i(v_j)-1)\pi< \vartheta (1,a_j) < i(v_j)\pi \end{aligned}$$

(5.20)

and proves claim (5.14) of the lemma. $\square$

We recall the definition of the signed clockwise counts c(j, k; j) of meander crossings, from Sect. 2.

Lemma 5.3

The clockwise increase

$$\begin{aligned} \lfloor (\vartheta (1,a_k)-\vartheta (1,a_j))/\pi \rfloor =\vartheta (1,a_k)/\pi -\lfloor \vartheta (1,a_j))/\pi \rfloor \end{aligned}$$

(5.21)

of the angle $\vartheta (1,a)$ from $a=a_j$ to $a=a_k$ is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \ c(j,k;j)+1 , &{} \text { if }\ Q\mathcal {M}_{j\,j+1} \text { is odd } \,; \\ \\ \ c(j,k;j), &{} \text { if }\ Q\mathcal {M}_{j\,j+1} \text { is even } \,. \end{array}\right. } \end{aligned}$$

(5.22)

Proof

At $a=a_k$ we recall $\vartheta (1,a)/\pi \in \mathbb {N}_0$ from (5.13). This proves claim (5.21). It remains to prove claim (5.22).

From the proof of Lemma 5.2 we recall that $\vartheta (1,a_j)\,(\mathrm {mod}\,2\pi )$ is the (clockwise) tangent angle of the meander segment $\mathcal {M}_{j\,j+1}$ at j with the horizontal axis; see (5.10). For general $a_j<a\le a_k$, the angle $\vartheta (1,a)$ tracks the secant between j and $(w(1,a),w_x(1,a))\in \mathcal {M}_{j\,k}$ .

By definition, neither the clockwise crossing count c(j, k; j), nor the clockwise angular increase $\lfloor (\vartheta (1,a_k)-\vartheta (1,a_j))/\pi \rfloor$ depend on homotopies of the Jordan meander segment $\mathcal {M}_{jk}$, as long as the initial tangent angle $\vartheta (1,a_j)$ and the final secant $\vartheta (1,a_k)$ remain fixed. Therefore we may assume all crossings of the angle $\vartheta (1,a)\,(\mathrm {mod}\,\pi )$ through the levels $\pi /2$ to be transverse, and finite in number, for $a\in (a_j,a_k]$.

The two cases (5.22) at $a=a_j$ arise as follows. The even/odd parity of j at the up- or down-crossing j of the meander $\mathcal {M}$ determines whether the initial (clockwise) tangent $\vartheta (1,a_j)$ points down or up; see (5.15). The precise direction, however, and the even/odd quadrant on that side of the horizontal axis, remain undetermined. Suppose we artificially twist an initial tangent $\vartheta (1,a_j)$ from an odd quadrant at j to the even quadrant on the same side of the horizontal axis. We do not require this twist to be realized by specific nonlinearities $f=f(x,v,v_x))$ in (5.2); we just compensate our twist, locally, by a homotopy of the initial meander segment $\mathcal {M}_{j\,j+1}$ near j. Then our twist of the initial tangent contributes one additional clockwise crossing to the crossing count c(j, k; j). Since this modification leaves (5.22) invariant, we may assume the initial tangent $\vartheta (1,a_j)$ to be in an odd quadrant, without loss of generality, i.e.

$$\begin{aligned} \lfloor \vartheta (1,a_j))/\pi \rfloor +\tfrac{1}{2}<\vartheta (1,a_j)/\pi <\lfloor \vartheta (1,a_j))/\pi \rfloor +1\,. \end{aligned}$$

(5.23)

Therefore (5.21), (5.23) ensure that $\lfloor (\vartheta (1,a_k)-\vartheta (1,a_j))/\pi \rfloor -1$ counts the net clockwise crossings of the angle $\vartheta (1,a)\,(\mathrm {mod}\,\pi )$ through the levels $\pi /2$, as a increases from $a=a_j$ to $a=a_k$ . This coincides with the clockwise crossing count c(j, k; j), by definition, and proves the lemma. $\square$

Contractibility of the winding map (5.12) allows us to identify the values of $\vartheta$ in lemmata 5.1–5.3 as real numbers, not just $\mathrm {mod}\,2\pi$. The lemmata therefore combine to show the NSL property (5.1) as follows. We first express $z_{j\,k}=\vartheta (1,a_k)/\pi$ in (5.13) of Lemma 5.1 via (5.21) of Lemma 5.3. We then substitute the two floor function expressions in (5.21) by (5.22) and (5.14), respectively. This proves our original claim (5.1). We may therefore evaluate $\vartheta (1,a_k)$ in (5.13) via summation of (5.11) and (5.21), to complete the proof of the NSL property (5.1).

Appendix: Meander Suspensions

The double cone suspension ${\widetilde{\mathcal {A}}}$ of a global attractor $\mathcal {A}$ is the topological quotient of $\mathcal {A}\times [0,1]$ obtained by identifying $\mathcal {A}\times 0$ and $\mathcal {A}\times 1$ to distinct disjoint points, called cone points. The unstable suspension of global attractors is an efficient tool for the study of their geometric properties (see for example [11]), and has also been considered in the related setting of meanders (see [26]). In this Appendix we define the corresponding suspension of a meander $\mathcal {M}$ and review some results encoded in the boundary value orderings of the equilibria in their Sturm global attractors.

Let ${\widetilde{\mathcal {M}}}$ denote the suspension of the meander $\mathcal {M}$ obtained by rotating the segment $\mathcal {M}_{1\,N}$ by $180^\circ$ and adding two extreme intersection points, labeled by $j=0$, left, and $j=N+1$, right, and two maximal outermost arcs. See Fig. 8,7 for an illustration.

Fig. 8

Canonical form of the suspension ${\widetilde{\mathcal {M}}}$ of the meander $\mathcal {M}$ corresponding to the permutation $\sigma = \{ 1 \ 4 \ 5 \ 6 \ 3 \ 2 \ 7 \}$. The meander segment ${\widetilde{\mathcal {M}}}_{1\,7}$ corresponds to a $180^\circ$ rotation of the segment $\mathcal {M}_{1\,7}$. The suspended meander ${\widetilde{\mathcal {M}}}$ corresponds to the permutation ${\widetilde{\sigma }} = \{ 0 \ 7 \ 2 \ 3 \ 6 \ 5 \ 4 \ 1 \ 8 \}$

As we show in Lemma 6.1 below, the suspension ${\widetilde{\mathcal {M}}}$ of a Sturm meander is again Sturm and the corresponding global attractor ${\widetilde{\mathcal {A}}}$ is connection equivalent to a double cone unstable suspension of the global attractor $\mathcal {A}$. Let ${\widetilde{\mathcal {E}}}$ denote the set of equilibria of ${\widetilde{\mathcal {A}}}$ and ${\widetilde{h}}_0,{\widetilde{h}}_1:\{0,\dots ,N+1\}\rightarrow {\widetilde{\mathcal {E}}}$ their boundary orders as obtained from the suspension ${\widetilde{\mathcal {M}}}$. Due to the rotation of the meander segment $\mathcal {M}_{1\,N}$, the correspondence $h_0(j)=v_j\mapsto {\widetilde{v}}_j:={\widetilde{h}}_0(j), j=1,\dots ,N$, preserves the $h_0$-order and reverses the $h_1$. Moreover, as we will show, the first equilibrium ${\widetilde{v}}_0:={\widetilde{h}}_0(0)$ and the last equilibrium ${\widetilde{v}}_{N+1}:={\widetilde{h}}_0(N+1)$ constitute the cone points of ${\widetilde{\mathcal {A}}}$.

Lemma 6.1

Let ${\widetilde{\mathcal {M}}}$ denote the meander suspension of the Sturm meander $\mathcal {M}$. Then, ${\widetilde{\mathcal {M}}}$ is a Sturm meander. Moreover, the Morse indices of the equilibria in ${\widetilde{\mathcal {E}}}$ and their zero number relations satisfy

$$\begin{aligned} i({\widetilde{v}}_0)= & {} i({\widetilde{v}}_{N+1})=0 \ , \quad i({\widetilde{v}}_j) = i(v_{j})+1 \text{ for } \ 1\le j\le N \ , \end{aligned}$$

(6.1)

$$\begin{aligned} z({\widetilde{v}}_j-{\widetilde{v}}_k)= & {} z(v_j-v_k)+1 \ \text{ for } \ 1\le j<k\le N , \end{aligned}$$

(6.2)

$$\begin{aligned} z({\widetilde{v}}_0-{\widetilde{v}}_j)= & {} 0 \ \text{ for } \ 1\le j\le N+1 , \quad z({\widetilde{v}}_k-{\widetilde{v}}_{N+1})=0 \ \text{ for } \ 0\le k\le N \,. \end{aligned}$$

(6.3)

Proof

Let $\sigma :=h_0^{-1}\circ h_1$ and ${\widetilde{\sigma }}:={\widetilde{h}}_0^{-1}\circ {\widetilde{h}}_1$ denote the permutations corresponding to the Sturm meanders $\mathcal {M}$ and ${\widetilde{\mathcal {M}}}$, respectively. Let ${\widetilde{\sigma }}'$ denote the restriction of ${\widetilde{\sigma }}$ to the set $\{1,\dots ,N\}$. By our definition of meander suspension, the meander segment ${\widetilde{\mathcal {M}}}_{1\,N}$ corresponds to a $180^\circ$ rotation of $\mathcal {M}_{1\,N}$. This implies that ${\widetilde{\sigma }}'=\kappa \sigma$, where $\kappa$ is the reversal involution. Therefore, we have

$$\begin{aligned} {\widetilde{\sigma }}(0)= & {} 0 \ , \quad {\widetilde{\sigma }}(N+1)=N+1 \ , \quad {\widetilde{\sigma }}(j)=\sigma (N+1-j) \ \text{ for } 1\le j\le N \,, \end{aligned}$$

(6.4)

$$\begin{aligned} {\widetilde{\sigma }}^{-1}(j)= & {} \sigma ^{-1}\kappa (j)=N+1-\sigma ^{-1}(j) \ \text{ for } 1\le j\le N \,. \end{aligned}$$

(6.5)

To show that ${\widetilde{\sigma }}\in S_{N+2}$ is a Sturm permutation, we compute the corresponding Morse numbers ${\widetilde{i}}_j, j=0,\dots ,N+1$, using the recursion (2.1) in this setting:

$$\begin{aligned} {\widetilde{i}}_0=0 \ , \quad {\widetilde{i}}_{j+1} = {\widetilde{i}}_j + (-1)^j{\text {sign}}\left( {\widetilde{\sigma }}^{-1}(j+1)-{\widetilde{\sigma }}^{-1}(j)\right) \ \text{ for } 0\le j\le N \,. \end{aligned}$$

(6.6)

In terms of the permutation $\sigma$, by (6.5), this recursion becomes

$$\begin{aligned} {\widetilde{i}}_{j+1} = {\widetilde{i}}_j + (-1)^j{\text {sign}}\left( \sigma ^{-1}(j)-\sigma ^{-1}(j+1)\right) \ \text{ for } 1\le j<N \,. \end{aligned}$$

(6.7)

A comparison between (6.7) and (2.1) then shows that both recursions, ${\widetilde{i}}_j$ and $i_j$, have the same step increments,

$$\begin{aligned} {\widetilde{i}}_{j+1}-{\widetilde{i}}_j = i_{j+1}-i_j \ \text{ for } \text{ all } 1\le j<N \,. \end{aligned}$$

(6.8)

Now, these recursions start at $j=1$ with $i_1=0$ and ${\widetilde{i}}_1=1$, by (6.6). Therefore, (6.8) shows that ${\widetilde{i}}_j=i_j+1$ for all $1\le j\le N$. It follows that ${\widetilde{i}}_N=1$, and (6.6) again implies ${\widetilde{i}}_{N+1}=0$. This shows that ${\widetilde{\mathcal {M}}}$ is a Sturm meander and proves (6.1).

Next, to prove the zero number relations (6.2)–(6.3) we invoke (2.5), alias the nonlinear Sturm-Liouville property (5.1) in the appendix Sect. 5.

Let $c=c(j,k;\ell )$ and ${\tilde{c}}={\tilde{c}}(j,k;\ell )$ denote the crossing numbers of $\mathcal {M}_{1\,N}$ and ${\widetilde{\mathcal {M}}}_{0\,N+1}$, respectively. We first note that the suspension does not affect the meander orientation. In fact, both meander segments $\mathcal {M}_{1\,N}$ and ${\widetilde{\mathcal {M}}}_{1\,N}$ are oriented by the increasing labels along $h_0$ and ${\widetilde{h}}_0$, respectively. Since $\mathcal {M}_{1\,N}$ and ${\widetilde{\mathcal {M}}}_{1\,N}$ are equal up to rotation, all the crossing numbers are preserved by the meander suspension, i.e. we have

$$\begin{aligned} {\widetilde{c}}(j,k;\ell ) = c(j,k;\ell ) \ \text{ for } \text{ all } 1 \le j,k,\ell \le N \,. \end{aligned}$$

(6.9)

The zero number relations for the equilibria ${\widetilde{v}}_1,\dots ,{\widetilde{v}}_N\in {\widetilde{\mathcal {E}}}$ are then obtained directly from (2.5). For all $0\le j<k\le N+1$, we have

$$\begin{aligned} z({\widetilde{v}}_k-{\widetilde{v}}_j) = {\left\{ \begin{array}{ll} i({\widetilde{v}}_j) + {\widetilde{c}}(j,k;j), &{} \text { if } Q{\widetilde{\mathcal {M}}}_{j\,j+1} \text { is odd } ; \\ \\ i({\widetilde{v}}_j) - 1 + {\widetilde{c}}(j,k;j), &{} \text { if } Q{\widetilde{\mathcal {M}}}_{j\,j+1} \text { is even } . \end{array}\right. } \end{aligned}$$

(6.10)

In addition, for $1\le j<N$ the quadrants $Q{\widetilde{\mathcal {M}}}_{j\,j+1}$ and $Q\mathcal {M}_{j\,j+1}$ have the same even/odd parity. Indeed, the parity of the quadrants is not affected by the $180^\circ$ rotation. Then, by (6.1) and (6.9), from (6.10) we obtain for all $1\le j<k\le N$

$$\begin{aligned} z({\widetilde{v}}_k-{\widetilde{v}}_j) = {\left\{ \begin{array}{ll} i(v_j) + 1 + c(j,k;j), &{} \text { if } Q\mathcal {M}_{j\,j+1} \text { is odd } ; \\ \\ i(v_j) + c(j,k;j), &{} \text { if } Q\mathcal {M}_{j\,j+1} \text { is even } . \end{array}\right. } \end{aligned}$$

(6.11)

Hence, comparing (6.11) with (2.5) for the equilibria $v_1,\dots ,v_N\in \mathcal {E}$, we obtain (6.2).

Finally, to prove (6.3) we invoke again (2.5) for the suspended meander ${\widetilde{\mathcal {M}}}$, alias (6.10). By the definition of meander suspension, the quadrant $Q{\widetilde{\mathcal {M}}}_{0\,1}$ of the first arc segment of ${\widetilde{\mathcal {M}}}$ is odd. Moreover, $i({\widetilde{v}}_0)=0$ for the extremal equilibrium ${\widetilde{v}}_0$, and the crossing numbers of ${\widetilde{\mathcal {M}}}_{0\,k}$ with respect to $\ell =0$ satisfy

$$\begin{aligned} {\widetilde{c}}(0,k;0) = 0 \ \text{ for } \text{ all } 1 \le k\le N+1 \,. \end{aligned}$$

(6.12)

Therefore, (6.10) with $j=0$ implies

$$\begin{aligned} z({\widetilde{v}}_k-{\widetilde{v}}_0) = i({\widetilde{v}}_0) + {\widetilde{c}}(0,k;0) = 0 \ \text{ for } \text{ all } 1\le k\le N+1 \,. \end{aligned}$$

(6.13)

Similarly, for the extremal equilibrium ${\widetilde{v}}_{N+1}$, we obtain

$$\begin{aligned} z({\widetilde{v}}_{N+1}-{\widetilde{v}}_j) = 0 \ \text{ for } \text{ all } 0\le j\le N \,. \end{aligned}$$

(6.14)

This proves (6.3), and completes the lemma. $\square$

Let $\mathcal {E}^*:={\widetilde{\mathcal {E}}}\setminus \{{\widetilde{v}}_0,{\widetilde{v}}_{N+1}\}$ and let $\mathcal {H}^*$ denote the set of heteroclinic orbits between the equilibria in $\mathcal {E}^*$, i.e. the connecting orbits $v\leadsto w$ with $v,w\in \mathcal {E}^*$. Let $\mathcal {A}^*\subset {\widetilde{\mathcal {A}}}$ denote the subset of all equilibria in $\mathcal {E}^*$ and all their connecting orbits in $\mathcal {H}^*$,

$$\begin{aligned} \mathcal {A}^* := \mathcal {E}^* \cup \mathcal {H}^* \,. \end{aligned}$$

(6.15)

Then, $\mathcal {A}^*$ is a flow invariant subset of ${\widetilde{\mathcal {A}}}$ which, by the transversality of stable and unstable manifolds, is the union of invariant submanifolds of ${\widetilde{\mathcal {A}}}$.

By our previous Lemma 6.1, the suspension has the effect of increasing all Morse indices by one, as asserted by (6.1). Moreover, the uniform increase by one of all the zero number relations between the equilibria, displayed by (6.2), shows that the suspension preserves the heteroclinic structure of the global attractor. Hence, the suspension correspondence $\mathcal {E}\mapsto \mathcal {E}^*$ determined by $v_j\mapsto {\widetilde{v}}_j, j=1,\dots ,N$, implies the connection equivalence between the global attractor $\mathcal {A}$ and the subset $\mathcal {A}^*\subset {\widetilde{\mathcal {A}}}$, i.e. the corresponding oriented connection graphs are isomorphic,

$$\begin{aligned} \mathcal {A}\sim \mathcal {A}^* \,. \end{aligned}$$

(6.16)

The zero number relations (6.3) then concern the orbits contained in ${\widetilde{\mathcal {A}}}\setminus \mathcal {A}^*$. In particular, for each ${\widetilde{v}}_j\in \mathcal {E}^*\subset \mathcal {A}^*$, (6.3) and the parabolic comparison principle imply that the one-dimensional fast unstable manifold $W^1({\widetilde{v}}_j)$ is the union of ${\widetilde{v}}_j$ itself, with two heteroclinic orbits: one connecting to ${\widetilde{v}}_0$, ${\widetilde{v}}_j\leadsto {\widetilde{v}}_0$, and the other connecting to ${\widetilde{v}}_{N+1}$, ${\widetilde{v}}_j\leadsto {\widetilde{v}}_{N+1}$. Therefore, $\mathcal {A}^*$ stands unstably suspended between the two extremal equilibria, ${\widetilde{v}}_0$ and ${\widetilde{v}}_{N+1}$, introduced by the meander suspension. See Fig. 9 for an illustration.

Fig. 9

Illustration of the unstable suspension of the global attractor $\mathcal {A}$. The cones are topologically glued at their bases where they share an invariant subset $\mathcal {A}^*$ which is connection equivalent to the global attractor $\mathcal {A}$, $\mathcal {A}^*\sim \mathcal {A}$. The cone points $\mathbf {\widetilde{N}}$ and $\mathbf {\widetilde{S}}$ correspond to the extremal equilibria ${\widetilde{v}}_0$ and ${\widetilde{v}}_{N+1}$

The next Lemma 6.2 addresses the behavior of the minimax property under the meander suspension.

Lemma 6.2

Let ${\widetilde{\mathcal {O}}}\in {\widetilde{\mathcal {E}}}\setminus \{{\widetilde{v}}_0,{\widetilde{v}}_{N+1}\}$ denote the equilibrium corresponding to any unstable $\mathcal {O}\in \mathcal {E}$ by the suspension mapping $v_j\mapsto {\widetilde{v}}_j, j=1,\dots ,N$. Then we have the following correspondences between target subsets and minimax equilibria, respectively:

$$\begin{aligned} \mathcal {E}^{n-1}_\pm (\mathcal {O}) \mapsto \mathcal {E}^n_\pm ({\widetilde{\mathcal {O}}}) \ , \quad \underline{v}^{\,\iota }_{\,\pm }(\mathcal {O}) \mapsto \underline{v}^{\,\iota }_{\,\pm }({\widetilde{\mathcal {O}}}) \ , \ {\overline{v}}^{\,\iota }_{\,\pm }(\mathcal {O}) \mapsto {\overline{v}}^{\,\iota }_{\,\pm }({\widetilde{\mathcal {O}}}) \ , \ \iota \in \{0,1\} \,. \end{aligned}$$

(6.17)

Proof

The suspended equilibria correspondence $\mathcal {E}^{n-1}_\pm (\mathcal {O}) \mapsto \mathcal {E}^n_\pm ({\widetilde{\mathcal {O}}})$, follows directly from (6.3) of Lemma 6.1 and the connection equivalence $\mathcal {A}\sim \mathcal {A}^*$, since the meander suspension preserves the $h_0$-order. The same arguments prove the correspondences $\underline{v}^{\,\iota }_{\,\pm }(\mathcal {O})\mapsto \underline{v}^{\,\iota }_{\,\pm }({\widetilde{\mathcal {O}}})$ and ${\overline{v}}^{\,\iota }_{\,\pm }(\mathcal {O})\mapsto {\overline{v}}^{\,\iota }_{\,\pm }({\widetilde{\mathcal {O}}})$ for $\iota \in \{0,1\}$, and complete the proof of (6.17) and the lemma. $\square$

In conclusion, this lemma shows that the Morse index $n=i(\mathcal {O})$ can indeed be assumed odd, without any loss, in our proof of Theorem 1.1. In fact, if the minimax property $\underline{v}^\iota _\pm (\mathcal {O})={\overline{v}}^{1-\iota }_\pm (\mathcal {O})$ holds for odd Morse index $i(\mathcal {O})$, Lemma 6.2 asserts that the minimax property $\underline{v}^{\,\iota }_{\,\pm }({\widetilde{\mathcal {O}}})={\overline{v}}^{\,1-\iota }_{\,\pm }({\widetilde{\mathcal {O}}})$ holds for even Morse index $i({\widetilde{\mathcal {O}}})=i(\mathcal {O})+1$.

As a final observation we mention that the $180^\circ$ rotation introduced in our definition of meander suspension is not necessary. In fact, Lemma 6.1 and also Lemma 6.2 conveniently adapted, hold as well for a meander suspension defined without the rotation of the meander segment $\mathcal {M}_{1\,N}$.