Abstract
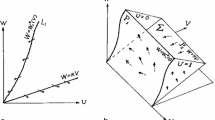
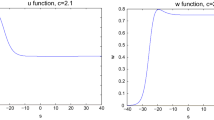
We use a shooting method to show the existence of traveling wave fronts and to obtain an explicit expression of minimum wave speed for a class of diffusive predator–prey systems. The existence of traveling wave fronts indicates the existence of a transition zone from a boundary equilibrium to a co-existence steady state and the minimum wave speed measures the asymptotic speed of population spread in some sense. Our approach is a significant improvement of techniques introduced by Dunbar. The advantage of our method is that it does not need the notion of Wazewski’s set and LaSalle’s invariance principle used in Dunbar’s approach. In our approach, we convert the equations for traveling wave solutions to a system of first order equations by a “non-traditional transformation”. With this converted new system, we are able to construct a Liapunov function, which gives an immediate implication of the boundedness and convergence of the relevant class of heteroclinic orbits. Our method provides a more efficient way to study the existence of traveling wave solutions for general predator–prey systems.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Diekmann O.: Run for your life: a note on the asymptotic speed of propagation of an epidemic. J. Diff. Equ. 33, 58–73 (1979)
Dunbar S.R.: Traveling wave solutions of diffusive Lotka-Volterra equations. J. Math. Biol. 17, 11–32 (1983)
Dunbar S.R.: Traveling wave solutions of diffusive Lotka-Volterra equations: a heteroclinic connection in R 4. Trans. Am. Math. Soc. 286, 557–594 (1984)
Fife P.C.: Mathematical aspects of reacting and diffusing systems, lecture notes in biomath., 28. Springer-Verlag, New York (1979)
Huang J., Lu G., Ruan S.: Existence of traveling wave solutions in a diffusive predator–prey model. J. Math. Biol. 46, 132–152 (2003)
Huang W., Han M.: Non-linear determinacy of minimum wave speed for a Lotka-Volterra diffusive competition model. J. Diff. Equ. 251, 1549–1561 (2011)
Lewis M., Li B., Weinberger H.: Spreading speed and linear determinacy for two-species competition models. J. Math. Biol. 45, 219–233 (2002)
Li B., Weinberger H., Lewis M.: Spreading speeds as slowest wave speeds for cooperative systems. Math. Biosci. 196, 82–98 (2005)
Li W., Wu S.: Traveling waves in a diffusive predator–prey model with holling type-III functional response. Chaos Solitons Fractals 37, 476–486 (2008)
Liang X., Zhao X.Q.: Asymptotic speed of pread and traveling waves for monotone semiflows with applications. Commun. Pure Appl. Math. 60, 1–40 (2007)
Lin, X., Wu, C., Weng, P.: Traveling wave solutions for a predator–prey system with sigmoidal response function. J. Dynam. Diff. Equ. (2011) (to appear)
Liu R., Feng Z., Zhu H., DeAngelis D.L.: Bifurcation analysis of a plant-herbivore model with toxin-determined functional response. J. Diff. Equ. 245, 442–467 (2008)
Mischaikow K., Reineck J.F.: Traveling waves in predator–prey systems. SIAM J. Math. Anal. 24, 1179–1214 (1993)
Murray J.D.: Mathematical biology. Springer-Verlag, New York (1993)
Okubo A., Levin S.A.: Diffusion and Ecological Problems, Modern Prespectives. Springer-Verlag, New York (2001)
Volpert, A.I., Volpert, V.A., Volpert, V.A.: Traveling Waves solutions of parabolic systems. Trans. Math. Monogr. Am. Math. Soc. 140 (1994)
Weinberger H.F.: Long time behavior of a class of biological models. SIAM J. Math. Anal. 13, 353–396 (1982)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Huang, W. Traveling Wave Solutions for a Class of Predator–Prey Systems. J Dyn Diff Equat 24, 633–644 (2012). https://doi.org/10.1007/s10884-012-9255-4
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-012-9255-4