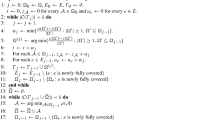Abstract
In this paper, we study the minimum partial set multi-cover problem (PSMC). Given an element set E, a collection of subsets \({\mathcal {S}}\subseteq 2^E\), a cost \(c_S\) on each set \(S\in {\mathcal {S}}\), a covering requirement \(r_e\) for each element \(e\in E\), and an integer k, the PSMC problem is to find a sub-collection \({\mathcal {F}}\subseteq {\mathcal {S}}\) to fully cover at least k elements such that the cost of \({\mathcal {F}}\) is as small as possible, where element e is fully covered by \({\mathcal {F}}\) if it belongs to at least \(r_e\) sets of \({\mathcal {F}}\). This paper presents an approximation algorithm using local ratio method achieving performance ratio \(\max \left\{ \frac{\Delta }{k}\left( \frac{1}{f-r_{\min }}+\frac{r_{\max }}{r_{\min }}\right) ,\frac{1}{\rho }+\frac{f}{r_{\min }}+\frac{1}{r_{\max }}-\frac{1}{\rho r_{\max }}-1,\frac{1}{\rho }\right\} \), where \(\Delta \) is the size of a maximum set, f is the maximum number of sets containing a common element, \(\rho \) is the minimum percentage of elements required to be fully covered during iterations of the algorithm, and \(r_{\max }\) and \(r_{\min }\) are the maximum and the minimum covering requirement, respectively. In particular, when \(r_{\max }\) is a constant, the first term can be omitted. Notice that our ratio coincides with the classic ratio f for both the set multi-cover problem (in which case \(k=|E|\)) and the partial set single-cover problem (in which case \(r_{\max }=1\)). However, when \(k<|E|\) and \(r_{\max }>1\), the ratio might be as large as \(\Theta (n)\). This result shows an interesting “shock wave like” feature of approximating PSMC. The purpose of this paper is trying to arouse some interest in such a feature and attract more work on this challenging problem.
Similar content being viewed by others
References
Bar-Yehuda R, Even S (1985) A local-ratio theorem for approximating the weighted vertex cover problem. Ann Discret Math 25:27–46
Bar-Yehuda R (2001) Using homogeneous weights for approximating the partial cover problem. J Algorithms 39:137–144
Bshouty NH, Burroughs L (1998) Massaging a linear programming solution to give a 2-approximation for a generalization of the vertex cover problem. In: The proceedings of the 15th annual symposium on the theoretical aspects of computer science, pp 298–308
Chvatal V (1979) A greedy heuristic for the set-covering problem. Math Oper Res 4:233–235
Dinh TN, Shen Y, Nguyen DT, Thai MT (2014) On the approximability of positive influence dominating set in social networks. J Comb Optim 27:487–503
Dobson G (1982) Worst-case analysis of greedy heuristics for integer programming with nonnegative data. Math Oper Res 7:515–531
Feige U (1996) A threshold of ln \(n\) for approximating set cover. In: Proceedings of the 28th ACM symposium on the theory of computing, pp 312–318
Fisher ML, Wolsey LA (1982) On the greedy heuristic for continuous covering and packing problems. SIAM J Algeb Discret Methods 3:584–591
Gandhi R, Khuller S, Srinivasan A (2004) Approximation algorithms for partial covering problems. J Algorithms 53(1):55–84
Halperin E, Srinivasan A (2002) Improved approximation algorithms for the partial vertex cover problem. In: 5th international workshop on approximation algorithms for combinatorial optimization problems, LNCS, vol 2462, pp 161–174
Hochbaum DS (1982) Approximation algorithms for the set covering and vertex cover problems. SIAM J Comput 11:555–556
Hochbaum DS (1998) The \(t\)-vertex cover problem: extending the half integrality framework with budget constraints, In: Proceedings of the first international workshop on approximation algorithms for combinatorial optimization problems, pp 111–122
Johnson DS (1974) Approximation algorithms for combinatorial problems. J Comput Syst Sci 9:256–278
Karp RM (1972) Reducibility among combinatorial problems. In: Miller RE, Thatcher JW (eds) Complexity of computer computations. Plenum Press, New York, pp 85–103
Kearns MJ (1990) The computational complexity of machine learning. MIT Press, Cambridge
Kolliopoulos SG (2003) Approximating covering integer programs with multiplicity constraints. Discret Appl Math 129:461–473
Kolliopoulos SG, Young Neal E (2005) Approximation algorithms for covering/packing integer programs. J Comput Syst Sci 71:495–505
Lovász L (1975) On the ratio of optimal integral and fractional covers. Discret Math 13:383–390
Ouali ME, Fohlin H, Srivastav A (2016) An approximation algorithm for the partial vertex cover problem in hypergraphs. J Comb Optim 31:846–864
Rajagopalan S, Vazirani VV (1993) Primal-dual RNC approximation algorithms for (multi)-set (multi)-cover and covering integer programs. In: Proceedings of the 34th annual IEEE symposium on foundations of computer science. Palo Alto, CA, pp 322–331
Ran YL, Zhang Z, Du HW, Zhu YQ (2016) Approximation algorithm for partial positive influence problem in social network. J Comb Optim. doi:10.1007/s10878-016-0005-0
Rawitz D, Shahar SH (2011) Partial multicovering and the d-consecutive ones property. Discret Optim 4:555–567
Slavík P (1997) Improved performance of the greedy algorithm for partial cover. Inf Process Lett 64(5):251–254
Srinivasan A (1996) An extension of the Lovász local lemma and its applications to integer programming. In: Proceedings of the seventh ACM-SIAM symposium on discrete algorithms, pp 6–15
Srinivasan A (1999) Improved approximations guarantees for packing and covering integer programs. SIAM J Comput 29:648–670 (preliminary version in Proc. STOC 95)
Srinivasan A, Teo C-P (2001) A constant-factor approximation algorithm for packet routing and balancing local versus global criteria. SIAM J Comput 30:2051–2068 (preliminary version in Proc. STOC 97)
Vazirani VV (2001) Approximation algorithms. Springer, Berlin
Wang F, Camacho E, Xu K (2009) Positive influence dominating set in online social networks. COCOA, LNCS, vol 5573, pp 313–321
Wang F, Du H, Camacho E, Xu K, Lee W, Shi Y, Shan S (2011) On positive influence dominating sets in social networks. Theor Comput Sci 412:265–269
Zhang W, Wu W, Wang F, Xu K (2011) Positive influence dominating sets in power-law graphs. Soc Netw Anal Min 2:31–37
Acknowledgments
This research is supported by NSFC (11531011).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ran, Y., Shi, Y. & Zhang, Z. Local ratio method on partial set multi-cover. J Comb Optim 34, 302–313 (2017). https://doi.org/10.1007/s10878-016-0066-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-016-0066-0