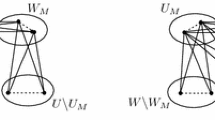Some results on the reciprocal sum-degree distance of graphs

Abstract

In this contribution, we first investigate sharp bounds for the reciprocal sum-degree distance of graphs with a given matching number. The corresponding extremal graphs are characterized completely. Then we explore the $k$-decomposition for the reciprocal sum-degree distance. Finally, we establish formulas for the reciprocal sum-degree distance of join and the Cartesian product of graphs.

1 Introduction

Throughout the paper, we consider finite undirected simple connected graphs. Let $G=(V,E)$ be a graph, we denote simply the order and size with $|V|$ and $|E|$ if no ambiguity can arise. The degree of a vertex $u\in V$ is the number of edges incident to $u,$ denoted by $\mathrm{deg }_{G}(u)$. The maximum and minimum vertex degree in the graph $G$ will be denoted by $\Delta (G)$ and $\delta (G),$ respectively. The distance between two vertices $u$ and $v$ is the length of a shortest path connecting them in $G,$ denoted by $\mathrm{dist }_{G}(u,v)$. The maximum value of such numbers, $\mathrm{diam }(G)$, is said to be the diameter of $G$. A matching of a graph $G$ is a set of edges with no shared endpoints. A maximal matching in a graph is a matching whose cardinality cannot be increased by adding an edge. The matching number $\beta (G)$ is the number of edges in a maximum matching.

The link, denoted by $(G_{1}\sim G_{2})(a\cdot b),$ of two disjoint graphs $G_{1}$ and $G_{2}$ is the graph obtained by joining $a\in V(G_{1})$ and $b\in V(G_{2})$ by an edge. Other terminology and notations needed will be introduced as it naturally occurs in the following and we use (Bondy and Murty 1976) for those not defined here.

The motivation for studying the quantity that the authors intend to call reciprocal (sum)-degree distance and reciprocal product-degree distance of a graph respectively, comes from the following observation. The sum of distances between all pairs of vertices in a graph $G$ is the Wiener index (Wiener 1947a), namely

$$\begin{aligned} W=W(G)=\sum _{\{u,v\}\subseteq V(G)}\mathrm{dist }_{G}(u,v), \end{aligned}$$

(1)

was first time introduced by Wiener more that 60 years ago (Wiener 1947a). Initially, the Wiener index $W(G)$ was considered as a molecular-structure descriptor used in chemical applications, but soon it attracted the interest of pure mathematicians (Entringer et al. 1976); for details and additional references see the review (Dobrynin et al. 2001) and the recent papers (Caporossi et al. 2012; Li et al. 2011; Wiener 1947b, c).

Eventually, a number of modifications of the Wiener index were proposed, which we present in the following table:

In Table 1, $W$ is the ordinary Wiener index, Eq. (1), whereas

$$\begin{aligned} DD_+ = DD_+(G)&= \sum _{\{u,v\}\subseteq V(G)} \big [\deg _G(u)+\deg _G(v)\big ]\mathrm{dist }_G(u,v) \end{aligned}$$

(2)

$$\begin{aligned} DD_* = DD_*(G)&= \sum _{\{u,v\}\subseteq V(G)} \big [\deg _G(u)\cdot \deg _G(v)\big ]\mathrm{dist }_G(u,v) \end{aligned}$$

(3)

$$\begin{aligned} H = H(G)&= \sum _{\mathop {\{u,v\}\subseteq V(G)}\limits _{u \ne v}} \frac{1}{\mathrm{dist }_G(u,v)} \end{aligned}$$

(4)

The graph invariants defined via Eqs. (2)–(4) have all been much studied in the past. The invariant $DD_+$ was first time introduced by Dobrynin and Kochetova (1994) and named (sum)-degree distance. Later the same quantity was examined under the name “Schulz index” (Gutman 1994). For mathematical research on degree distance see (Ilić et al. 2011; Tomescu 2010) and the references cited therein. A remarkable property of $DD_+$ is that in the case of trees of order $n$, the identity $DD_+ =4W - n(n-1)$ holds (Klein et al. 1992).

Table 1 A family of distance- and degree-based graph invariants

In Gutman (1994) it was shown that also the multiplicative variant of the degree distance, namely $DD_*$ , Eq. (3), obeys an analogous relation: $DD_* = 4W - (2n-1)(n-1)$. This latter quantity is sometimes referred to as the “Gutman index” (see Feng and Liu 2011; Mukwembi 2012; and the references quoted therein), but here we call it product-degree distance.

The greatest contributions to the Wiener index, Eq. (1), come from most distant vertex pairs. Because in many applications of graph invariants it is preferred that the contribution of vertex pairs diminishes with distance, the Wiener index was modified according to Eq. (4). This distance-based graph invariant is called Harary index and was introduced in the 1990s by Plavšić et al. (1993). It also was subject of numerous mathematical studies (see Cui and Liu 2012; Xu 2012; Xu and Das 2011; Zhou et al. 2008; and the references cited therein).

The graph invariants, defined via Eqs. (1)–(4), can be arranged as in Table 1. From this Table it is immediately seen that one more such invariants are missing.

In Su et al. (2012a) introduced the reciprocal product-degree distance of graphs, which can be seen as a product-degree-weight version of Harary index:

$$\begin{aligned} RDD_* = RDD_*(G)&= \sum _{\mathop {\{u,v\}\subseteq V(G)}\limits _{u \ne v}} \frac{\deg _{G}(u)\cdot \deg _{G}(v)}{\mathrm{dist }_G(u,v)} . \end{aligned}$$

(5)

They mainly determined the connected graph of given order with maximum $RDD_*$-value, and established various lower and upper bounds for $RDD_*$ in terms of matching, independence number, vertex-connectivity and other topological invariants.

Hua and Zhang (2012) proposed a new graph invariant named reciprocal degree distance (here we call it reciprocal sum-degree distance), which can be seen as a (sum)-degree-weight version of Harary index:

$$\begin{aligned} RDD_+ = RDD_+(G)&= \sum _{\mathop {\{u,v\}\subseteq V(G)}\limits _{u \ne v}} \frac{\deg _{G}(u)+\deg _{G}(v)}{\mathrm{dist }_G(u,v)} \ . \end{aligned}$$

(6)

In (Hua and Zhang 2012) they mainly presented some extremal properties of reciprocal degree distance. However, to our best knowledge, the $RDD_{+}$-value of connected graphs with a given matching number has not been considered by other authors so far. In this contribution, we first investigate sharp bounds of the reciprocal sum-degree distance of graphs with a given matching number. The extremal graphs also determined completely. Then we explore the $k$-decomposition of the complete graph $K_{n}$ for the reciprocal sum-degree distance. Formulas for the reciprocal sum-degree distance of join and the Cartesian product graphs were also established.

2 $RDD_{+}$-value with given matching number

Let $G-e$ denote the graph formed from $G$ by deleting an edge $e\in E,$ and $G+e$ denote the one obtained from $G$ by adding an edge $e\in \overline{E}$.

Lemma 2.1

(Hua and Zhang 2012) Let $G$ be a connected graph of order $n$ at least three. Each of the following holds:

(a):

if $G$ is not isomorphic to $K_{n}$ (the complete graph of order $n$), then $RDD_{+}(G)<RDD_{+}(G+e)$ for any $e\in E(\overline{G});$

(b):

if $G$ has an edge $e$ not being a bridge, then $RDD_{+}(G)>RDD_{+}(G-e)$.

A component of a graph is said to be odd (resp., even) if it has odd (resp., even) number of vertices. Indicate the number of odd components by $o(G)$.

The following is an immediate consequence of the Tutte-Berge formula (Lovász and Plummer 1986).

Lemma 2.2

(Lovász and Plummer 1986) Let $G$ be a connected graph of order $n$. Then

$$\begin{aligned} n-2\beta =\max \{o(G-X)-|X|:X\subset V\}. \end{aligned}$$

Let $\mathcal Q (n,\beta )$ denote the class of connected graphs of order $n$ with matching number $\beta$.

Lemma 2.3

Let $G$ be a connected graph of order $n\ge 4$ with matching number $\beta \in [2,\lfloor \frac{n}{2}\rfloor ]$. Let

$$\begin{aligned} \sigma =\frac{23-4n+\sqrt{37n^{2}-121n+109}}{21}. \end{aligned}$$

Each of the following holds:

(a):

if $\beta =\lfloor \frac{n}{2}\rfloor ,$ then $RDD_{+}(G)\le n(n-1)^{2},$ with equality if and only if $G=K_{n};$

(b):

if $\sigma <\beta \le \lfloor \frac{n}{2}\rfloor -1,$ then $RDD_{+}(G)\le 4\beta ^{3}+(2n-12)\beta ^{2}+(11-3n)\beta +\frac{n^{2}-n-4}{2},$ with equality if and only if $G=K_{1}+(K_{2\beta -1}\cup \overline{K_{n-2\beta }});$

(c):

if $\beta =\sigma ,$ then $RDD_{+}(G)\le 4\sigma ^{3}+(2n-12)\sigma ^{2}+(11-3n)\sigma +\frac{n^{2}-n-4}{2} =\frac{1}{2}\sigma ^{3}-\frac{1}{2}\sigma ^{2}+\frac{n^{2}-3n+2}{2}\sigma ,$ with equality if and only if $G=K_{\beta }+\overline{K_{n-\beta }}$ or $G=K_{1}+(K_{2\beta -1}\cup \overline{K_{n-2\beta }});$

(d):

if $2\le \beta <\sigma ,$ then $RDD_{+}(G)\le \frac{1}{2}\beta ^{3}-\frac{1}{2}\beta ^{2}+\frac{n^{2}-3n+2}{2}\beta ,$ with equality if and only if $G=K_{\beta }+\overline{K_{n-\beta }}$.

Proof

Let $G^{\prime }$ be a connected graph with maximum $RDD_{+}$-value in $\mathcal Q (n,\beta )$. From Lemma 2.2, it follows that there exists a vertex subset $X^{\prime }\subset V(G^{\prime })$ such that

$$\begin{aligned} n-2\beta =\max \{o(G^{\prime }-X)-|X|:X\subset V\}=o(G^{\prime }-X^{\prime })-|X^{\prime }|. \end{aligned}$$

For simplicity, let $|X^{\prime }|=s$ and $o(G^{\prime }-X^{\prime })=t$. Then $n-2\beta =t-s$.

• Case I. $s=0$.

In this case, $G^{\prime }-X^{\prime }=G^{\prime }$ and then $n-2\beta =t\le 1$. By our choice of $G$ and Lemma 2.1, we obtain that $G^{\prime }= K_n,$ then we have $RDD_{+}(G^{\prime })= n(n-1)^{2}$.

• Case II. $s\ge 1$.

Consequently, $t\ge 1$. Let $G^\mathrm{o }_{1},G^\mathrm{o }_{2},\cdots ,G^\mathrm{o }_{t}$ be all the odd components of $G^{\prime }-X^{\prime }$. To obtain our result, we state and prove the following four claims.

• Claim 1. There is no even component in $G^{\prime }-X^{\prime }$.

To the contrary, let $G^\mathrm{e }$ be an even component. Then the link $(G^\mathrm{e }\sim G^\mathrm{o }_{i})(a\cdot b),$ obtained by joining a vertex $a\in V(G^\mathrm{e })$ and $b\in V(G^\mathrm{o }_{i}),$ is also an odd component in $G^{\prime }-X^{\prime }$. We denote such a graph by $G^{\prime \prime },$ for which $n-2\beta (G^{\prime \prime })\ge o(G^{\prime \prime }-X^{\prime })-|X^{\prime }|=o(G^{\prime }-X^{\prime })-|X^{\prime }|$ holds. This implies that $G^{\prime \prime } \in \mathcal Q (n,\beta ),$ which contradicts to the choice of $G^{\prime }$.

• Claim 2. Each odd component $G^\mathrm{o }_{i} (1\le i\le t),$ and the graph induced by $X^{\prime },$ are complete.

Assume that $G^\mathrm{o }_{i}$ is not complete. Then there must exist two non-adjacent vertices $u,v$ in $G^\mathrm{o }_{i}$. By Lemma 2.1, one can get a graph $G^{\prime }+uv,$ which increases the $RDD_{+}$-value. This again is a contradiction with the choice of $G^{\prime }$. Similarly, we can prove that $X^{\prime }$ is complete.$\square$

• Claim 3. Each vertex of $G^\mathrm{o }_{i}$ is adjacent to a vertex of $X^{\prime }$.

The proof follows as before.$\square$

Now, without loss of generality, we let $n_{i}=|V(G^\mathrm{o }_{i})|$ for $i=1,2,\cdots ,t$. Then by Claim 1, 2 and 3 we have

$$\begin{aligned} G^{\prime }=K_{s}+(K_{n_{1}}\cup K_{n_{2}}\cup \cdots \cup K_{n_{t}}). \end{aligned}$$

Let $\widehat{RDD_{+}}(G_{1},G_{2})$ denote the contribution to the $RDD_{+}$-value between vertices of $G_{1}$ and those of $G_{2},$ then we have

$$\begin{aligned} \left\{ \begin{array}{l} \widehat{RDD_{+}}(K_{n_{i}},K_{n_{i}})=2{n_{i}\atopwithdelims ()2}(n_{i}+s-1),\\ \widehat{RDD_{+}}(K_{n_{i}},K_{n_{j}})=n_{i}n_{j}(n_{i}+s-1+n_{j}+s-1),\\ \widehat{RDD_{+}}(K_{n_{i}},K_{s})=sn_{i}(n-1+n_{i}+s-1),\\ \widehat{RDD_{+}}(K_{s},K_{s})=2{s\atopwithdelims ()2}(n-1).\\ \end{array}\right. \end{aligned}$$

Hence, the reciprocal sum-degree distance of $G^{\prime }$ can be represented as

$$\begin{aligned} RDD_{+}(G^{\prime })&= \sum _{i=1}^{t}\widehat{RDD_{+}}(K_{n_{i}},K_{n_{i}}) +\sum _{i<j}\widehat{RDD_{+}}(K_{n_{i}},K_{n_{j}})\\&\quad +\sum _{i=1}^{t}\widehat{RDD_{+}}(K_{n_{i}},K_{s})+\widehat{RDD_{+}}(K_{s},K_{s})\\&= \sum _{i=1}^{t}n_{i}^{3}+(2s-2)\sum _{i=1}^{t}n_{i}^{2}+(s^{2}+(n-3)s+1)\sum _{i=1}^{t}n_{i}\\&\quad +\sum _{i<j}n_{i}n_{j}(n_{i}+n_{j}+2s-2)+2{s\atopwithdelims ()2}(n-1). \end{aligned}$$

We also need claim 4 below, which can be verified by Lagrange multiplier.

• Claim 4. Each of the following function

$$\begin{aligned} \left\{ \begin{array}{l} \mathrm F _{1}(n_{1},n_{2},\cdots ,n_{t})=n_{1}^{3}+n_{2}^{3}+\cdots +n_{t}^{3}\\ \mathrm F _{2}(n_{1},n_{2},\cdots ,n_{t})=n_{1}^{2}+n_{2}^{2}+\cdots +n_{t}^{2}\\ \mathrm F _{3}(n_{1},n_{2},\cdots ,n_{t})=n_{1}+n_{2}+\cdots +n_{t}\\ \mathrm F _{4}(n_{1},n_{2},\cdots ,n_{t})=\sum _{i<j}n_{i}n_{j}(n_{i}+n_{j}+2s-2) \end{array}\right. \end{aligned}$$

attains its maximum under the conditions $n_{1}+n_{2}+\cdots +n_{t}=n-s$ and $1\le n_{1}\le n_{2}\le \cdots \le n_{t}$ if and only if $n_{1}=n_{2}=\cdots =n_{t-1}=1$ and $n_{t}=2\beta -2s+1$.

By Claim 4, we get

$$\begin{aligned} RDD_{+}(G^{\prime })&= \mathrm F _{1}(n_{1},n_{2},\cdots ,n_{t})+2(s-1)\mathrm F _{2}(n_{1},n_{2},\cdots ,n_{t})\\&\quad +(s^{2}+(n-3)+1)\mathrm F _{3}(n_{1},n_{2},\cdots ,n_{t})+\frac{1}{2}\mathrm F _{4}(n_{1},n_{2},\cdots ,n_{t}), \end{aligned}$$

which attains its maximum if and only if $n_{1}=n_{2}=\cdots =n_{t-1}=1$ and $n_{t}=n-s-t+1=2\beta -2s+1$.

It follows that

$$\begin{aligned} G^{\prime }=K_{s}+(K_{2\beta -2s+1}\cup \overline{K_{n+s-2\beta -1}}). \end{aligned}$$

Simple calculations shows that

$$\begin{aligned} \left\{ \begin{array}{l} \widehat{RDD_{+}}(K_{2\beta -2s+1},K_{2\beta -2s+1})=2{2\beta -2s+1\atopwithdelims ()2}(2\beta -s),\\ \widehat{RDD_{+}}(\overline{K_{n+s-2\beta -1}},\overline{K_{n+s-2\beta -1}})={n+s-2\beta -1\atopwithdelims ()2}s,\\ \widehat{RDD_{+}}(K_{2\beta -2s+1},\overline{K_{n+s-2\beta -1}})=(2\beta -2s+1)(n+s-2\beta -1)\beta ,\\ \widehat{RDD_{+}}(K_{s},K_{s})=2{s\atopwithdelims ()2}(n-1). \end{array}\right. \end{aligned}$$

Taking into account the contributions to the $RDD_{+}$-value above, it follows that

$$\begin{aligned} RDD_{+}(G^{\prime })&= \widehat{RDD_{+}}(K_{2\beta -2s+1},K_{2\beta -2s+1}) +\widehat{RDD_{+}}(\overline{K_{n+s-2\beta -1}},\overline{K_{n+s-2\beta -1}})\\&\quad +\widehat{RDD_{+}}(K_{2\beta -2s+1},\overline{K_{n+s-2\beta -1}})+\widehat{RDD_{+}}(K_{s},K_{s})\\&= -\frac{7}{2}s^{3}+\frac{4n+24\beta -1}{2}s^{2}+\frac{n^{2}-5n-24\beta ^{2}-8n\beta +4}{2}s\\&\quad +4\beta ^{3}+2n\beta ^{2}+(n-1)\beta . \end{aligned}$$

Analyzing the function $\Phi$ on $s$

$$\begin{aligned} \Phi (s)&= -\frac{7}{2}s^{3}+\frac{4n+24\beta -1}{2}s^{2}+\frac{n^{2}-5n-24\beta ^{2}-8n\beta +4}{2}s+4\beta ^{3}\\&\quad +2n\beta ^{2}+(n-1)\beta . \end{aligned}$$

It follows that $s\le \beta ,$ since $t-s= n-2\beta \ge t+s-2\beta$. By taking derivatives, we have

$$\begin{aligned}&\Phi ^{\prime }(s)=-\frac{21}{2}s^{2}+(4n+24\beta -1)s+\frac{n^{2}-5n-24\beta ^{2}-8n\beta +4}{2}~\text {and}\\&\Phi ^{\prime \prime }(s)=-21s+4n+24\beta -1=21(\beta -s)+4n+3\beta -1\ge 4n+3\beta -1>0. \end{aligned}$$

This implies that $\Phi (s)$ is a strictly convex function for $s\le \beta ,$ and the maximum value of $\Phi (s)$ is attained when $s=1$ or $s=\beta$.

$$\begin{aligned}&\Phi (1)=4\beta ^{3}+(2n-12)\beta ^{2}-(3n-11)\beta +\frac{n^{2}-n-4}{2}~\text {and}\\&\Phi (\beta )=\frac{1}{2}\beta ^{3}-\frac{1}{2}\beta ^{2}+\frac{n^{2}-3n+2}{2}\beta . \end{aligned}$$

After subtraction, we obtain

$$\begin{aligned} \Phi (1)-\Phi (\beta )=\frac{7}{2}\beta ^{3}+\frac{4n-23}{2}\beta ^{2}-\frac{n^{2}+3n-20}{2}\beta +\frac{n^{2}-n-4}{2}. \end{aligned}$$

Now, let us consider the function $\Psi$ on $\beta$

$$\begin{aligned} \Psi (\beta )=\frac{7}{2}\beta ^{3}+\frac{4n-23}{2}\beta ^{2}-\frac{n^{2}+3n-20}{2}\beta +\frac{n^{2}-n-4}{2}. \end{aligned}$$

It follows that

$$\begin{aligned} \Psi ^{\prime }(\beta )=\frac{21}{2}\beta ^{2}+(4n-23)\beta -\frac{n^{2}+3n-20}{2}. \end{aligned}$$

The quadratic equation $\Psi ^{\prime }(\beta )=0$ has two distinct roots, since $37n^{2}-121n+109>0$. Let $\sigma$ be its positive root, namely

$$\begin{aligned} \sigma =\frac{23-4n+\sqrt{37n^{2}-121n+109}}{21}. \end{aligned}$$

If $\beta >\sigma ,$ and $\Psi ^{\prime }(\beta )>0,$ then $\Psi (\beta )$ is an increasing function, and $\Psi (\beta )>\Psi (1)=0$ follows. This implies that $\Phi (1)>\Phi (\beta )$. If $\beta <\sigma ,$ then $\Phi (1)<\Phi (\beta )$. This completes the proof of Theorem 2.3.$\square$

3 $K$-decomposition for $RDD_{+}$

Let $k$ be an integer not less than $2,$ a k -decomposition $\mathcal D _{k}=(G_{1}, G_{2},\cdots , G_{k})$ of a graph $G$ is a partition of its edge set to form $k$ spanning subgraphs $G_{1}, G_{2}, \cdots , G_{k},$ each of the $G_{i}$ is said to be a cell of $G$. We encourage the interested reader to refer (Aouchiche and Hansen 2013; Nordhaus and Gaddum 1956) for some more information.

Li and Zhao (2004) introduced the concept of the generalized first Zagreb index for a graph, which was defined as: $M_{1,\epsilon }(G)=\sum _{v\in V}[\mathrm{deg }_{G}(v)]^{\epsilon }$. In particular, $M_{1,2}(G)=M_{1}(G)$ is the first Zagreb index. We encourage the interested reader to consult (Ashrafi et al. 2011; Došlić and Bonchev 2008; Klein et al. 2007) for details on these indices.

Lemma 3.1

(Su et al. 2012b) Let $\mathcal D _{k}$ be a $k$-decomposition of the complete graph $K_{n}$ and $t$ be an integer. Then

(a):

$n(n-1)^{\epsilon }k^{1-\epsilon }\le \sum _{i=1}^{k}M_{1,\epsilon }(G_{i})\le n(n-1)^{\epsilon },~\text {if}~ \epsilon > 1;$

(b):

$n(n-1)^{\epsilon }\le \sum _{i=1}^{k}M_{1,\epsilon }(G_{i})\le n(n-1)^{\epsilon }k^{1-\epsilon },~\text {if}~ 0<\epsilon <1;$

(c):

$n(n-1)^{\epsilon }k^{1-\epsilon }\le \sum _{i=1}^{k}M_{1,\epsilon }(G_{i})\le n\big [t+t(n-2)^{\epsilon }\big ],~\text {if}~ \epsilon <0~\text {and}~ k=2t;$

(d):

$n(n-1)^{\epsilon }k^{1-\epsilon }\le \sum _{i=1}^{k}M_{1,\epsilon }(G_{i})\le n\big [t+(t+1)(n-2)^{\epsilon }\big ],~\text {if}~\epsilon <0~\text {and}~ k=2t+1$.

The following results will be used in our proofs.

Lemma 3.2

(Hua and Zhang 2012) Let $G$ be a connected graph of order $n\ge 2$ and $m\ge 1$. Then

$$\begin{aligned} \frac{2(n-1)m}{\mathrm{diam }(G)}+\frac{(\mathrm{diam }(G)-1)M_{1}(G)}{\mathrm{diam }(G)}\le RDD_{+}(G)\le (n-1)m+\frac{M_{1}(G)}{2}, \end{aligned}$$

with either equality if and only if $\mathrm{diam }(G)\le 2$.

Hua and Zhang characterized connected graphs with the maximum and minimum $RDD_{+}$-value, respectively. More precisely:

Lemma 3.3

(Hua and Zhang 2012) Among all nontrivial connected graphs of order n, the graphs with the maximum and minimum $RDD_{+}$-value are $K_{n}$ and $P_{n}$ (the path of order $n$), respectively.

This bring us to the main result in this section.

Theorem 3.4

Let $\mathcal D _{k}$ be a $k$-decomposition of the complete graph $K_{n}$. Then

$$\begin{aligned} kRDD_{+}(P_{n})\le \sum _{i=1}^{k}RDD_{+}(G_{i})\le n(n-1)^{2}, \end{aligned}$$

with left equality if and only if each cell $G_{i}\cong P_{n},$ and with right equality if and only if the diameter of $G_{i}$ is at most two.

Proof

Let $m_{i}$ denotes the size of the $i$-th cell $G_{i}$ of $\mathcal D _{k}$. By Lemmas 3.1 and 3.2, we get

$$\begin{aligned} \sum _{i=1}^{k}RDD_{+}(G_{i})&\le \sum _{i=1}^{k}\left[ (n-1)m_{i}+\frac{1}{2}M_{1}(G_{i})\right] \\&= (n-1)\sum _{i=1}^{k}m_{i}+\frac{1}{2}\sum _{i=1}^{k}M_{1}(G_{i})\\&\le n(n-1)^{2}. \end{aligned}$$

An et al. (2011) proved that for any sufficiently large $n$ with respect to $k$, there is a $k$-decomposition $\mathcal D _{k}$ of $K_{n}$ such that $\mathrm{diam }(G_{i})=2$ for each $i=1, 2,\cdots , k$. Hence the right equality holds if and only if the diameter of $G_{i}$ is at most two.

The lower bound can be verified directly by Lemma 3.3

$$\begin{aligned} \sum _{i=1}^{k}RDD_{+}(G_{i})\ge kRDD_{+}(P_{n}). \end{aligned}$$

This completes the proof of Theorem 3.4.$\square$

4 $RDD_{+}$-value for operation graphs

In this section we present formulas for computing $RDD_{+}$ of join and the Cartesian product of graphs.

4.1 Join graphs

The join $G_{1}+ G_{2}$ of graphs $G_{1}$ and $G_{2}$ with disjoint vertex sets $V_{1}$ and $V_{2}$ and edge sets $E_{1}$ and $E_{2}$ is the graph union $G_{1}\cup G_{2}$ together with all edges joining $V_{1}$ and $V_{2}$.

The following lemma is crucial in what follows later. For convenience, we use $|V_{i}|$ and $|E_{i}|$ to denote the order and the size of graph $G_{i}$ for $i=1,2,$ respectively.

Lemma 4.1

Let $G_{1}$ and $G_{2}$ be two connected graphs. Then we have

• (a) $|V(G_{1}+G_{2})|=|V_{1}|+|V_{2}|$ and $|E(G_{1}+G_{2})|=|E_{1}|+|E_{2}|+|V_{1}|\cdot |V_{2}|$.

• (b) The join of graphs is associative and commutative.

• (c) $\mathrm{deg }_{G_{1}+G_{2}}(u)=\mathrm{deg }_{G_{1}}(u)+|V_{2}|$ for $u\in V_{1}$ and $\mathrm{deg }_{G_{1}+G_{2}}(u)=\mathrm{deg }_{G_{2}}(v)+|V_{1}|$ for $v\in V_{2}$.

• (d)
  $$\begin{aligned} \mathrm{dist }_{G_{1}+G_{2}}(u_{1},u_{2})\!=\!\left\{ \begin{array}{l} 0,\quad \text {if}~u_{1}=u_{2},\\ 1,\quad \text {if}~u_{1}u_{2}\in E_{1}~\text {or}~u_{1}u_{2}\in E_{2}~\text {or}~(u_{1}\in V_{1}~\text {and}~u_{2}\in V_{2}),\\ 2,\quad \text {otherwise}. \end{array}\right. \end{aligned}$$

Proof

The claims (a)–(d) are derived from the definitions and some well known results of the book of Imrich and Klavžar (2000).$\square$

Let $\widehat{RDD_{+}}_{+}(G_{i},G_{i})$ (resp., $\widehat{RDD_{+}}_{*}(G_{i},G_{i})$) denote the contribution to the $RDD_{+}$-value by adjacent (resp., non-adjacent) vertices in $G_{i}$ for $i=1,2,$ respectively.

Theorem 4.2

Let $G=G_{1}+G_{2}$ be the join of two connected graphs $G_{1}$ and $G_{2}$. Then

$$\begin{aligned} RDD_{+}(G_{1}\!+\!G_{2})&\!=\!&M_{1}(G_{1})\!+\!M_{1}(G_{2})\!+\!\frac{1}{2}\overline{M}_{1}(G_{1}) \!+\!\frac{1}{2}\overline{M}_{1}(G_{2})\!+\!4|V_{2}|\cdot |E_{1}|\!+\!4|V_{1}|\\&\quad \cdot |E_{2}|+|V_{1}|\cdot |V_{2}|^{2}+|V_{1}|^{2}\cdot |V_{2}|+|V_{2}|\cdot |\overline{E}_{1}|+|V_{1}|\cdot |\overline{E}_{2}|, \end{aligned}$$

where $\overline{M}_{1}(G)$ is the first Zagreb co-index of graph $G$.

Proof

Simple calculations shows that

$$\begin{aligned} \left\{ \begin{array}{lll} \widehat{RDD_{+}}_{+}(G_{1},G_{1})&{}=&{}\sum _{uv\in E_{1}}\big [\mathrm{deg }_{G_{1}}(u)+\mathrm{deg }_{G_{1}}(v)+2|V_{2}|\big ]=M_{1}(G_{1})+2|V_{2}|\cdot |E_{1}|,\\ \widehat{RDD_{+}}_{+}(G_{2},G_{2})&{}=&{}\sum _{uv\in E_{2}}\big [\mathrm{deg }_{G_{2}}(u)+\mathrm{deg }_{G_{2}}(v)+2|V_{1}|\big ]=M_{1}(G_{1})+2|V_{1}|\cdot |E_{2}|,\\ \widehat{RDD_{+}}_{*}(G_{1},G_{1})&{}=&{}\sum _{uv\in \overline{E}_{1}}\big [\mathrm{deg }_{G_{1}}(u)+\mathrm{deg }_{G_{1}}(v)+2|V_{2}|\big ]\cdot \frac{1}{2}=\frac{1}{2}\overline{M}_{1}(G_{1})+|V_{2}|\cdot |\overline{E}_{1}|,\\ \widehat{RDD_{+}}_{*}(G_{2},G_{2})&{}=&{}\sum _{uv\in \overline{E}_{2}}\big [\mathrm{deg }_{G_{2}}(u)+\mathrm{deg }_{G_{2}}(v)+2|V_{1}|\big ]\cdot \frac{1}{2} =\frac{1}{2}\overline{M}_{1}(G_{2})+|V_{1}|\cdot |\overline{E}_{2}|,\\ \widehat{RDD_{+}}(G_{1},G_{2})&{}=&{}\sum _{u\in V_{1}}\sum _{v\in V_{2}}\big [\mathrm{deg }_{G_{1}}(u)+\mathrm{deg }_{G_{2}}(v)+|V_{1}|+|V_{2}|\big ]\\ &{}=&{}2|V_{2}|\cdot |E_{1}|+2|V_{1}|\cdot |E_{2}|+|V_{1}|^{2}\cdot |V_{2}|+|V_{1}|\cdot |V_{2}|^{2}. \end{array}\right. \end{aligned}$$

Hence, the reciprocal sum-degree distance of $G_{1}+G_{2}$ can be written as the sum

$$\begin{aligned} RDD_{+}(G)&= \widehat{RDD_{+}}_{+}(G_{1},G_{1})+\widehat{RDD_{+}}_{+}(G_{2},G_{2}) +\widehat{RDD_{+}}_{*}(G_{1},G_{1})\\&\quad +\widehat{RDD_{+}}_{*}(G_{2},G_{2})+\widehat{RDD_{+}}(G_{1},G_{2})\\&= M_{1}(G_{1})+M_{1}(G_{2})+\frac{1}{2}\overline{M}_{1}(G_{1}) +\frac{1}{2}\overline{M}_{1}(G_{2})+4|V_{2}|\cdot |E_{1}|\\&\quad +4|V_{1}|\cdot |E_{2}| +|V_{1}|\cdot |V_{2}|^{2}+|V_{1}|^{2}\cdot |V_{2}|+|V_{2}|\cdot |\overline{E}_{1}|+|V_{1}|\cdot |\overline{E}_{2}|. \end{aligned}$$

This completes the proof of Theorem 4.2.$\square$

Let $K_{s,t}$ be the bipartite graph with two partitions having $s$ and $t$ vertices. Note that $K_{s,t}=\overline{K}_{s}+\overline{K}_{t},$ we have:

Corollary 4.3

$RDD_{+}(K_{s,t})=RDD_{+}(\overline{K}_{s}+\overline{K}_{t})=st^{2}+s^{2}t+s{t\atopwithdelims ()2}+t{s\atopwithdelims ()2}$.

4.2 Cartesian product graphs

The Cartesian product $G_{1}\square G_{2}$ of graphs $G_{1}$ and $G_{2}$ is a graph with vertex set $V_{1}\times V_{2},$ and two vertices $(u_{1},u_{2})$ and $(v_{1},v_{2})$ adjoint by an edge:

$$\begin{aligned} (u_{1},u_{2})\sim (v_{1},v_{2})\Leftrightarrow \left\{ \begin{array}{lll} u_{1}=v_{1}~\text {and}~u_{2}\sim v_{2}~\text {in}~G_{2}, \\ \text {or}\\ u_{2}=v_{2}~\text {and}~u_{1}\sim v_{1}~\text {in}~G_{1}. \\ \end{array}\right. \end{aligned}$$

Lemma 4.4

Let $G_{1}$ and $G_{2}$ be two connected graphs. Then we have

(a):

$|V(G_{1}\square G_{2})|=|V_{1}|\cdot |V_{2}|$ and $|E(G_{1}\square G_{2})|=|V_{1}|\cdot |E_{2}|+|V_{2}|\cdot |E_{1}|$.

(b):

$\mathrm{deg }_{G_{1}\square G_{2}}(u,v)=\mathrm{deg }_{G_{1}}(u)+\mathrm{deg }_{G_{2}}(v);$

(c):

$\mathrm{dist }_{G_{1}\square G_{2}}((u^{\prime }, u^{\prime \prime }),(v^{\prime }, v^{\prime \prime }))=\mathrm{dist }_{G_{1}}(u^{\prime },v^{\prime })+\mathrm{dist }_{G_{2}}(u^{\prime \prime },v^{\prime \prime })$.

Proof

The claims (a)–(c) are derived from the definitions and some well known results of the book of Imrich and Klavžar Imrich and Klavžar (2000).$\square$

Theorem 4.5

Let $G=G_{1}\square G_{2}$ be the Cartesian product of graphs $G_{1}$ and $G_{2}$. Then

$$\begin{aligned} RDD_{+}(G_{1}\square G_{2})\!\le \! |V_{2}|RDD_{+}(G_{1})\!+\!|V_{1}|RDD_{+}(G_{2})\!+\!4|E_{1}|H(G_{2})\!+\!4|E_{2}|H(G_{1}). \end{aligned}$$

Proof

Let $u=(u^{\prime },u^{\prime \prime })$ and $v=(v^{\prime },v^{\prime \prime })$ be two vertices in $G=G_{1}\square G_{2}$. By the definition of $RDD_{+}$ and Lemma 4.4, we have

$$\begin{aligned} RDD_{+}(G_{1}\square G_{2})&= \sum _{\{u,v\}\in V(G)}\frac{\mathrm{deg }_{G_{1}\square G_{2}}(u) +\mathrm{deg }_{G_{1}\square G_{2}}(v)}{\mathrm{dist }_{G_{1}\square G_{2}}(u,v)}\\&= \sum _{\{u,v\}\in V(G)}\frac{\mathrm{deg }_{G_{1}}(u^{\prime })+\mathrm deg _{G_{2}}(u^{\prime \prime }) +\mathrm{deg }_{G_{1}}(v^{\prime })+\mathrm{deg }_{G_{2}}(v^{\prime \prime })}{\mathrm{dist }_{G_{1}}(u^{\prime },v^{\prime })+\mathrm{dist }_{G_{2}}(u^{\prime \prime },v^{\prime \prime })}\\&\le \sum _{a\in V_{1}}\sum _{\{u^{\prime \prime }, v^{\prime \prime }\}\in V_{2}}\left[ \frac{\mathrm{deg }_{G_{1}}(u^{\prime }) +\mathrm{deg }_{G_{1}}(v^{\prime })}{\mathrm{dist }_{G_{2}}(u^{\prime \prime },v^{\prime \prime })}+\frac{\mathrm{deg }_{G_{2}}(u^{\prime \prime }) +\mathrm{deg }_{G_{2}}(v^{\prime \prime })}{\mathrm{dist }_{G_{2}}(u^{\prime \prime },v^{\prime \prime })}\right] \\&\quad +\sum _{b\in V_{2}}\sum _{\{u^{\prime }, v^{\prime }\}\in V_{1}}\left[ \frac{\mathrm{deg }_{G_{1}}(u^{\prime }) +\mathrm{deg }_{G_{1}}(v^{\prime })}{\mathrm{dist }_{G_{1}}(u^{\prime },v^{\prime })}+\frac{\mathrm{deg }_{G_{2}}(u^{\prime \prime }) +\mathrm{deg }_{G_{2}}(v^{\prime \prime })}{\mathrm{dist }_{G_{1}}(u^{\prime },v^{\prime })}\right] \\&= |V_{2}|RDD_{+}(G_{1})+|V_{1}|RDD_{+}(G_{2})+4|E_{1}|H(G_{2})+4|E_{2}|H(G_{1}). \end{aligned}$$

This completes the proof of Theorem 4.5.$\square$