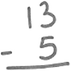Introduction

A sixth-grade student, Chloe, has solved a problem involving subtraction of mixed numbers. Chloe’s work, shown in Fig. 1, makes evident that she has arrived at an incorrect answer.

Fig. 1
figure 1

Chloe’s work on a mixed number subtraction problem

Full size image

How might a teacher respond to Chloe’s work? A novice teacher, relying on their own experiences of mathematics as a subject of clear-cut right and wrong answers, might focus on the fact that Chloe arrived at an incorrect answer and aim to help Chloe find and correct her mistake (Ball 1989). By focusing on remediation and prioritizing the correct answer, the teacher would learn little about the process Chloe was using, Chloe’s understanding of that process, or Chloe’s understanding of relevant concepts like the meaning of mixed number notation. Moreover, the teacher would not learn whether Chloe’s incorrect answer was the result of a minor mistake or reflective of a deeper conceptual misunderstanding. As a result, the teacher would have minimal information on which to base decisions for subsequent instruction.

Another teacher, perhaps a teacher more familiar with common patterns in students’ mathematical thinking, might recognize that an incorrect answer does not necessarily preclude mathematical understanding. Such a teacher might engage in a line of questioning to elicit more information about Chloe’s thinking before drawing conclusions and making instructional decisions. For example, a teacher might learn that Chloe was trying to subtract three-fifths from two-fifths but realized she did not have enough, so she borrowed from the 3. The teacher might then wonder whether Chloe is overgeneralizing “borrowing” from work with subtracting multi-digit numbers or whether she has made a record-keeping error. The teacher could ask Chloe to explain the value of the “little one” in fraction notation, which could lead Chloe to realize that she has made a mistake. Then, Chloe might reflect on the source of the mistake, such as forgetting that she was borrowing five-fifths, not ten. From such an interaction, a teacher could gather important information that helps to characterize Chloe’s mathematical knowledge and understanding accurately and to interpret the significance of this particular incorrect answer in terms of Chloe’s mathematical development. However, for a teacher to obtain this nuanced and detailed information about a student’s mathematical thinking by asking about work on a particular problem, the teacher must have a sense of the mathematical territory involved and be curious about the student’s thinking.

Defining a problem of practice

The opening scenario illustrates a recurring problem of practice in mathematics teaching: A student has produced an incorrect answer, and the teacher must interpret what that incorrect answer might indicate about the student’s mathematical knowledge and skill more broadly in order to determine how to respond instructionally. There are multiple reasons that a student might arrive at an incorrect answer, and each reason has different instructional implications. For example, a student might produce an incorrect answer that is, in fact, a correct answer to a different question (Ginsburg 1997). Clarifying the question would be a possible instructional response. Alternatively, a student could make what Bass (personal communication, 2018) terms a “bookkeeping” error, where the error occurs in the process of recording one’s work or in carrying out a familiar procedure. Radatz (1980) refers to such an error as a mistake, because it is an isolated and unrepresentative mis-execution of an algorithm (i.e., a careless move) as opposed to a systematic and persistent mis-execution that reflects a conceptual or procedural misunderstanding. This suggests the additional possibility that a student may arrive at an incorrect answer due to a conceptual or procedural misunderstanding. Recognizing that scholars (e.g., Borasi 1994; Mellone et al. 2015; Radatz 1980; Santagata 2005; Smith III et al. 1993) have defined errors and mistakes in a variety of ways, we use the terms interchangeably. We include additional description when we mean to isolate a particular type of error. Our point, as the opening exploration of Chloe’s work demonstrates, is that an incorrect answer to a mathematics problem can have a range of possible sources and instructional implications. Eliciting a student’s understanding is necessary for teachers to ascertain the nature of the situation.

In addition, interactions around incorrect student responses can be powerful sites of learning for both teachers and students (Borasi 1994; Hiebert et al. 1997; Mellone et al. 2015; Smith III et al. 1993). When an answer is incorrect, the joint sense-making required to interpret student thinking can go beyond the identification and correction of mistakes or errors into the conceptual analysis of why the mistake or error was made (Borasi 1994; Cooper 2009; Kazemi and Stipek 2001). The information that teachers can uncover by eliciting students’ thinking can then guide their pedagogical response. Further, framing mistakes and incorrect answers as valued contributions to learning can help shape positive mathematics identities for learners (Aguirre et al. 2013) and contribute to equitable instruction (NCTM 2018). We recognize that different types of errors and incorrect responses can offer different opportunities for learning. In order to capitalize on student responses that do offer particularly generative sites for learning, teachers need to be familiar with a range of sources and meanings for errors and incorrect answers (Stockero and Van Zoest 2013).

While the importance of interacting with students around errors and mistakes is well documented, research suggests that practicing teachers vary greatly in their attention to and treatment of errors and mistakes in the classroom (Bray 2011; Brodie 2014; Santagata 2005; Silver et al. 2005). Researchers have also noted considerable variability in practicing teachers’ eliciting of students’ mathematical thinking beyond initially asking, “How did you get that?” (Franke et al. 2009). With regard to prospective teachers (PTs), previous research shows that at the outset of teacher education, in a scenario in which a student uses a nonstandard approach and arrives at a correct answer, PTs may demonstrate the capability to elicit the steps of a student’s mathematical process but may be less likely to elicit the student’s understanding of relevant mathematical ideas (Shaughnessy and Boerst 2018a). Further, PTs may initially “fill in” student thinking, making inferences about what a student did or understands without eliciting that information from the student, or try to redirect a student to use a more familiar or conventional method (Shaughnessy and Boerst 2018a).

Though the field has some knowledge of how practicing teachers handle mistakes and how PTs elicit the mathematical thinking of a student with a correct answer, less is known about how PTs elicit student thinking when they see errors and incorrect answers. This matters for several reasons. When students produce work with an incorrect answer, PTs have the opportunity to learn something about the student and/or about mathematics, including common patterns of student thinking (Mellone et al. 2015). PTs can leverage this information in many ways. For example, learning more about a particular student can support a PT in targeting future instructional interactions. Likewise, learning more about common patterns of student thinking can support PTs in anticipating how students will interact with mathematical tasks and in designing lessons that surface common patterns of student thinking for analysis and learning (Smith and Stein 2011). Additionally, when students make what seem to be mistakes, asking questions may reveal understandings that are not evident from their written work. This can challenge deficit-oriented assumptions about children’s mathematical thinking. As a set, these instances represent ways to break the widely held notion that mathematics is just about right or wrong answers (Boaler 2016).

Research focus

In this study, we examine PTs’ capabilities around a particular recurrent problem of practice: eliciting student thinking when a student has an incorrect answer. We explore a case in which the student makes a bookkeeping error, a mistake in their arithmetic process, and will recognize the mistake if asked specific questions about their reasoning. We selected a case with a bookkeeping error rather than a conceptual error for two main reasons. First, anecdotal findings from our prior work suggest that at the beginning of a teacher education program, PTs often equate correct answers to mathematics problems with a thorough understanding and incorrect answers with a lack of understanding. Therefore, we wanted to create a scenario that could raise PTs’ awareness that someone can arrive at an incorrect answer and still have a strong conceptual understanding. Further, we aimed to challenge common deficit-oriented interpretations of student thinking. We anticipated that an incorrect answer that resulted from a conceptual misunderstanding would lead PTs to focus exclusively on what the student seemed not to know or understand or to dismiss the student’s approach, thereby reinforcing a deficit-oriented perspective. In contrast, an incorrect answer resulting from a bookkeeping error creates an opportunity for PTs to realize that a student has a greater understanding than they may have anticipated.

We focus on the work of eliciting student thinking because a teacher’s eliciting around mistakes and incorrect answers can have significant implications for children’s learning. Limited eliciting of student thinking can reinforce deficit-oriented interpretations and lead teachers to pursue less ambitious learning goals (Battey and Franke 2015). In contrast, thorough eliciting of students’ mathematical thinking via probing questions can support teaching that affirms children’s sense-making and advances their mathematical reasoning (Aguirre et al. 2013; Ball 1988; Lampert et al. 2013). In general, teachers must gather and carefully consider information about what students know and understand in order to design instruction responsive to individual students and build on student strengths (Carpenter et al. 1996; Jacobs et al. 2010, 2011). In cases where a student has made a mistake or arrived at an incorrect answer, teachers’ understanding of the basis of children’s mistakes is necessary for instruction that is linked to students’ current understandings (Brodie 2014; Cooper 2009). In other words, in order to ascertain how to move a student’s understanding forward, teachers need to know whether an incorrect response is a mistake that occurred even though the student had a strong conceptual understanding or whether it reflects limited conceptual understanding. Some might approach interactions with a student around an incorrect answer with the goal of helping the student correct an error that has been made. For example, Jacobs and Ambrose (2008) describe a set of intentional instructional moves to support a student’s mathematical reasoning. In contrast, our work is focused on eliciting students’ thinking. Jacobs and Phillip (2004) have referred to eliciting student thinking as exploring the student’s thinking. We see eliciting student thinking as a precursor to responding to or extending a student’s thinking instructionally.

Research question

This study investigates the following research question: How do prospective teachers elicit the thinking of a student who has made a mistake? Specifically, we sought to analyze the extent to which PTs’ (a) elicited the full process used by the student; (b) elicited the student’s understanding of the process and mathematical ideas underlying that process; and (c) elicited the student’s mistake, including the reason for the mistake and their revised process. In this paper, we illustrate how knowledge of eliciting capability can be gathered through the use of a live simulation in which a PT interacts with a teacher educator who is taking on the role of a student. We discuss what such findings reveal about the capabilities of PTs in one teacher education program and the implications of these findings. In the next section, we explain why we chose to focus on PTs’ capabilities at the beginning of teacher preparation.

Focusing on PTs’ capabilities at the beginning of teacher preparation

There has been increasing focus on preparing PTs for the work of teaching by focusing on specific instructional practices (e.g., Ball and Forzani 2009; Ball et al. 2009; Cartun et al. 2018; Ghousseini and Herbst 2016; Jacobs and Phillip 2004; McDonald et al. 2013). In practice-based teacher education, learning goals for PTs are tied to developing capabilities with specific tasks carried out in teaching. We use the term capabilities to describe PTs’ ability to carry out specific aspects of the work of teaching at a particular point in time, fully intending that PTs’ capabilities will grow and change over time.

When helping PTs develop such capabilities, teacher educators would benefit from knowing what PTs bring with them to teacher education to be able to design the program in ways that anticipate and build on PTs’ prior ways of acting and interacting. Prior research provides knowledge of some of the orientations and assumptions that PTs bring to teacher preparation (Boyd et al. 2014; Foote et al. 2013; Richardson 1996; 2003) and their knowledge of subject-matter content (Ball 1990; Ma 1999). Research on particular teaching practices often focuses on student outcomes resulting from the use of a particular teaching practice (e.g., Fennema et al. 1996), composite parts of the teaching practice (e.g., Smith and Stein 2011), and/or challenges in learning to enact particular teaching practices (e.g., Ghousseini 2015). Such knowledge is useful for the design of teacher education; however, it is insufficient. We need knowledge of the capability with which PTs can enact particular teaching practices upon entry to a teacher education program.

We build on a prior study, mentioned above, that examined PTs’ capabilities with eliciting student thinking at the point of entry to a teacher education program (Shaughnessy and Boerst 2018a). In the prior study, PTs elicited the thinking of a student who arrived at a correct answer. This study focuses on the thinking of a student who arrives at an incorrect answer because of a bookkeeping error. We view the case of eliciting when a student has made a mistake as presenting substantively different opportunities for PTs. We wondered about how the PTs would elicit student thinking when the student arrived at an incorrect answer. In particular, we wondered whether PTs would be able to learn that the student could recognize that they had made a mistake and the student had a strong conceptual understanding of the process used and mathematical ideas underlying that process. Next, we unpack the teaching practice of eliciting student thinking.

The practice of eliciting student thinking

The practice of eliciting student thinking enables teachers to uncover student thinking. TeachingWorks (2019) describes the practice in the following way:

Teachers pose questions that create space for students to share their thinking about specific academic content. They seek to understand student thinking, including novel points of view, new ideas, ways of thinking, or alternative conceptions. Teachers draw out student thinking through carefully chosen questions and tasks and attend closely to what students do and say.

Eliciting student thinking makes the nature of students’ current knowledge available to the teacher. In other words, eliciting is about learning about the elements and details of a student’s thinking. Such information is essential for engaging students’ preconceptions and building on their existing knowledge (National Research Council 2000). Further, the practice of pushing students to explain their thinking in depth through asking student’s questions about their thinking is linked to students’ explaining more of their thinking in both whole class and in small group, even when a teacher is not present (Webb et al. 2019). Through such work, teachers “signal to students that they are knowledgeable and that their ideas are interesting and valued” (TeachingWorks 2019). In actual practice, eliciting student thinking is often done in conjunction with interpreting and responding to student thinking in ways that support students in building on their current understandings (Jacobs et al. 2010).

Because of the crucial nature of the practice and the need to teach novices to do this work, it is necessary to specify the work involved in eliciting student thinking. We conceive of the work of eliciting student thinking in mathematics as including initiating the interaction in a way that invites the student to share initial thinking, asking questions about what the student says and does, and eliciting key aspects of the student’s thinking, such as mathematical processes, strategies, understandings, and solutions (Shaughnessy and Boerst 2018b). We also maintain teachers must convey respect for students and their thinking by thoroughly following the path of the students’ own thinking before or instead of seeking to redirect the student’s thinking. In other words, we believe that students’ reasoning and sense-making should be the focus of eliciting. We recognize that our conception of eliciting student thinking contrasts with more traditional views of mathematics teaching (e.g., seeing the teacher’s role as telling or showing how to arrive at correct answers) that PTs may espouse when entering teacher education (Ball 1989). Thus, part of our work in supporting PTs is to build an understanding of eliciting student thinking as distinct from correcting answers or introducing particular strategies. We further specify the practice of eliciting student thinking by naming moves that are examples of work in each area (Boerst et al. 2011). We view PT’s enactment of particular moves as a means to assess their capabilities with the practice. Throughout this paper, we use “capability with eliciting student thinking” to refer to the degree to which PTs can engage in these areas of work.

Methods

Since 2011, members of our team have been studying PTs’ capability with eliciting student thinking through the use of teaching simulations. A simulation serves as an “approximation of practice” (Grossman et al. 2009). Simulations have been used in many professional fields such as medicine and nursing (Ainsworth 1991; Barrows 1993; Jeffries 2005) and, more recently, in the preparation of teachers (Dotger et al. 2010; Self 2016). In the simulations we design, a PT interacts with a “standardized student” (a teacher educator taking on the role of a student using a well-defined set of decision rules for responding) around a specific piece of written work.

Advantages of using simulations to assess PTs’ teaching capabilities

Our teaching simulation has advantages over field-based interviews for assessing capability with eliciting student thinking (Shaughnessy et al. 2019; Dotger et al. 2018). Field-based interviews leave the nature of the student thinking being elicited to chance and can be highly variable. In contrast, the teaching simulation uses highly specified protocols that enable us to control key aspects of the student’s process, understanding, and demeanor. This leads to comparable eliciting contexts for all of our PTs, which facilitates a fair and more nuanced assessment of PTs’ eliciting capability (Shaughnessy et al. 2019).

The simulation also has advantages over providing PTs with student work samples and having them articulate questions they might ask to learn more about students’ thinking. While this written form of assessment enables teacher educators to standardize the student thinking PTs are considering, it lacks the authenticity of interacting with a student in real time and limits the line of questioning PTs might pursue. Simulations, in contrast, allow PTs to engage in the practice of eliciting in a “live” interaction, which provides space for asking follow-up questions to clarify and probe student thinking. In sum, a simulation serves as an approximation of teaching practice (Grossman et al. 2009) in which teachers engage in authentic work in a way that provides a fair and reliable window into PTs’ developing capability with eliciting student thinking. Although simulations lack the complexity of a classroom context and provide just a snapshot of student thinking, they still provide useful insights into how PTs initially engage in eliciting work.

Structure of our teaching simulations

We design teaching simulations to have a consistent three-part format (Shaughnessy and Boerst 2018b). First, PTs are provided with a student’s work on a problem and given 10 min to prepare for an interaction. Second, PTs have 5 min to interact with the standardized student, eliciting the “student’s” thinking to understand the steps they took, the reasoning behind particular steps, and their understanding of the key mathematical ideas involved. In the event that they discover that the student has a misunderstanding about a mathematical idea, PTs are directed not to teach the student that idea or how to solve the problem.Footnote 1 Third, PTs are interviewed about their interpretations of the “student’s” process and understanding. In total, the assessment takes approximately 25 min.

The teaching simulation used in this particular study

We constructed a detailed student role profile, which included information about the student’s process for solving a particular mathematics problem, understanding, and way of being. The student role profile also included a set of scripted responses for questions that PTs are likely to pose (see a subset of scripted responses in Table 1). This student uses a nonstandard process for solving multi-digit subtraction problems, sometimes referred to as “Expand and Trade” (see the student work in Fig. 2). This process involves writing the value of the minuend and subtrahend in expanded form and making any necessary trades (i.e., regrouping). When used correctly, the user would then subtract the numbers place by place in expanded form. This student correctly applies the expanding and trading process, but mistakenly adds values by place instead of subtracting. The student has a conceptual understanding of (a) the expanded form, (b) the meanings of addition and subtraction, and (c) when, how, and why to make trades. In this particular instance, however, the student loses sight of the fact that they are solving a subtraction problem due to the addition symbols in expanded form. This mistake, akin to a bookkeeping error, is described in Everyday Mathematics teacher materials as a common occurrence to watch for (Bell et al. 2015).

Table 1 Excerpt from the student role profile. A subset of scripted responses
Full size table
Fig. 2
figure 2

Student work, the student makes a mistake

Full size image

Further, the student profile contains specific instances in which the student realizes that they have made a mistake and revises their thinking. We reasoned that having the student change their mind would bring greater authenticity to an interaction around a mistake. During the interaction, the student will change their mind when pressed to: make and evaluate an estimate for the original problem, represent their process with a picture, talk about the meaning of the operation in the original problem, explain why trades were made, solve another multi-digit subtraction problem, or resolve the original problem. The individuals carrying out the standardized student role were trained only to reveal the mistake or revise the process if pressed by the PT on these specific points.

A critical aspect of this student role profile design is that getting the student to realize they made a mistake and to revise their process is contingent upon the PT’s eliciting work. As a result of this design feature, there is the potential for considerable variation in the steps and ideas that PTs elicit. A PT demonstrating stronger eliciting capability could gather information about what the student does understand and why the student made the mistake they did. In contrast, someone with less developed capability might learn only the steps the student took to arrive at their incorrect answer. This variation would not be as visible if the student stuck with their initial process. Thus, this simulation assessment creates the opportunity to examine substantial variation in PTs’ capability with eliciting student thinking when the student has made a mistake.

Data collection

Participants

To investigate how PTs elicit student thinking in a case where a student has made a mistake, we engaged all PTs (n = 30) enrolled in the first year of an undergraduate university-based elementary teacher education program in the USA in the teaching simulation. Twenty-eight identified as female and two identified as male. Almost all were between the ages of 20–23 and 23% identified as people of color. The students were predominately middle class, with a few first-generation college students.

Procedures

All participants engaged in the teaching simulation during the first week of the teacher education program as a regular part of the program. PTs were assembled in a test room to complete written program assessments and pulled out individually to engage in the simulation. All enrolled PTs participated in the teaching simulation and consented to have their data used for research purposes. Three individuals were trained to carry out the role of the standardized student and conducted assessments simultaneously in separate assessment rooms. The teaching simulations were video-recorded. Written artifacts were collected.

Data analysis

We focused our analysis for this study on the interaction between PTs and the standardizad student. We used the software package Studiocode© to code the assessment video. We began by parsing the eliciting portion of the video into talk turns. Then we identified what we refer to as “instances,” which contain a question posed by a PT and the student’s response to that question.

We developed a set of codes that specify core components of the practice of eliciting student thinking. The codes include a combination of components that are quite obvious (e.g., elicitation of each step in the student’s original process), components of eliciting student thinking that we have observed and tracked over time (e.g., eliciting the student’s understanding of key mathematical ideas, Shaughnessy and Boerst 2018a, b; Shaughnessy et al. 2019), and components that emerged from analysis of the data for this specific eliciting task (e.g., surfacing that the student made a mistake, eliciting a revised process). We identified a host of specific “moves,” such as asking a question to elicit that the student compared numbers in each place to determine whether a trade was needed or asking a question to elicit the student’s understanding of why trading is needed. By “moves,” we mean instances of talk that teachers use for specific purposes as they interact with students (Chapin et al. 2013). Each move we identified was used as a code. These codes, including an example of each code, are listed in Table 2.

Table 2 Codes for appraising performance
Full size table

Companion codes were created for each eliciting move to track cases in which PTs made a statement about the student’s process or understanding and got the student to agree but did not first elicit that information from the student. We refer to such a move as “filling” the student’s thinking (Shaughnessy and Boerst 2018a). For example, if a PT said, “Did you get 878 by adding the numbers along the bottom here?” that instance would be coded as a fill for the student’s final step of adding the partial sums. Each question posed by a PT was coded as either a specific eliciting move or as filling in specific information about the student’s process or understanding. In other words, eliciting and filling codes were mutually exclusive as applied to specific information in each instance. In cases where a given step repeatedly occurs (e.g., expanding, comparing numbers in a given place, trading) or where a PT addressed the same understanding multiple times, an individual PT’s overall performance could receive both an eliciting code and a fill code for a given step or understanding. For example, if a PT elicited that the student traded 100 in one instance and then filled in that the student traded 10 in another instance, those instances would be coded with eliciting the trading step and filling the trading step, respectively. Therefore, eliciting codes and fill codes were not mutually exclusive across a performance. We included distinct codes for filling in student thinking because filling positions the student differently and limits the information that teachers can gather about student thinking.

Two members of the research team appraised each performance. All relevant codes were applied to each instance. Disagreements were resolved through a review of the data and remediating differences of interpretation by referencing a codebook. An illustration of two coded instances is provided in Table 3. In the first instance, note that the code applied is based on the information that the student revealed in their response (i.e., that the student expanded 583 to 500 + 80 + 3). In the second instance, note that both eliciting and fill codes were applied, but they refer to different pieces of information about the student’s thinking.

Table 3 Example of coded instances
Full size table

The next stage of analysis entailed exporting code frequencies to determine the presence or absence of each move in each performance. We then examined the prevalence of specific moves across the dataset. We organized the eliciting moves into three components: (a) eliciting the student’s original process for solving the problem, (b) eliciting the student’s understanding of key mathematical ideas, and (c) eliciting the student’s mistake, including the reason for the mistake and the revised answer.

Findings: what moves did PTs make when eliciting student thinking?

We present our findings according to the three main components of eliciting student thinking indicated above and in Table 2, unpacking eliciting around the student’s mistake in two parts (eliciting the mistake and following up after the student has revealed the mistake). For each component, we indicate the percentage of PTs who employed each of the moves, provide illustrative transcripts, and name the patterns that emerged.

Eliciting the student’s original process

The standardized student’s process has five steps: expanding the minuend and subtrahend, comparing numbers in each place, trading, adding (rather than subtracting) by place, and adding partial sums to arrive at the answer. Table 4 includes the percentage of PTs eliciting each step as well as the percentage of PTs filling each step (stating what they thought the student had done and then getting the student to agree or disagree). Some of these steps occurred more than once. For example, comparing the numbers in each place occurred in the hundreds, tens, and ones. When steps occurred multiple times, we looked for evidence that the PT had elicited (or filled) the step at least once. The highest rates of eliciting occurred around the first three steps of the student’s process: the expansion, the comparison of the numbers in each place, and the trading steps. When we examined individual PTs’ eliciting of multiple steps, we found that 7% of PTs elicited all five steps of the process, 27% elicited four of the five steps, 43% elicited three of the five steps, 13% elicited 2 of the five steps, 7% elicited one step, and 3% elicited none of the steps (Note: not shown in Table 4). Notably, only 53% elicited the step where the mistake was made—adding numbers by place in expanded form after trading. There are several possible reasons that PTs may not have asked about this step. For one, PTs may have recognized from the written work that the student made a mistake and therefore saw no reason to ask about it. Alternatively, PTs may have been uncomfortable asking about an error, perhaps worrying about how this might make the student feel. Additionally, PTs may have interpreted the simulation directions not to teach if they uncovered a misunderstanding as meaning they should not point out the error. The smallest percentage of eliciting occurred around the final step adding the partial sums (10%). This low percentage for the final step was not surprising given that (a) the addition of partial sums could be easily inferred from the written work and (b) the step occurred after the student made the mistake and may not have been relevant if the PT had asked questions which resulted in the student revealing that they had made a mistake.

Table 4 Percentage of PTs who elicited and filled each step of the student’s process
Full size table

Across our sample, PTs stating what they thought the student had done and then getting the student to agree or disagree—what we refer to as filling in the student’s thinking—occurred for several steps of the student’s process. To ensure consistency in the student thinking across the interactions, if a PT made an incorrect statement about the student’s thinking, the student would respond with “no” and state their actual thinking. Because the student did not confirm the filled information, we did not count such instances as fills and PTs received credit for eliciting the step. Examining each step of the student’s process, 10% of the PTs filled that the student compared numbers in each place for one or more comparisons, 30% filled that the student traded 100 for 10 tens and/or 10 for 10 ones, and 20% filled the student’s process for adding in expanded form once the trade had been made. Considering all of the steps, we found that 7% of the PTs filled three steps in the student’s process, 10% filled two steps, 43% filled one step, and 40% did not fill any steps during the interaction.

We next turn to an example that represents the common pattern of focusing eliciting on the first three steps and filling in at least one step. This PT initiated the interaction by asking the student to describe what they did step by step.

PT:

So can you tell me step by step what you did with this problem?

Student:

Sure. So, first I expanded 583 to 500 + 80 + 3

PT:

Okay

Student:

Um, and then I also expanded 295 to 200 + 90 + 5

After hearing that the student first expanded 583 and 295, the PT asked about the crossed-out 3 from 583.

PT:

Okay. And… from there, what is this? [points to crossed out 3]

Student:

So, after I expanded, I looked and saw that 500 was more than 200

PT:

Mm hmm

Student:

And then I saw that 80 was less than 90, so I need to make a trade

Upon hearing that the student compared the numbers in each place and saw they needed to make a trade, the PT asked a follow-up question about the trade was carried out. The PT used the language of “borrowing” to refer to trading.

PT:

Okay… So you borrowed from here?

Student:

Yeah, I took 100 from 500, which left 400. And I added 100 to 80, which gave me 180

After hearing the steps used by the student to make a trade, the PT asked about the operation in the problem.

PT:

Okay. And do you know if the problem asked for subtraction or addition?

Student:

It’s a subtraction problem

Although this may have been an attempt to probe the student’s mistake, the PT did not follow up on the connection between the student’s understanding of the operation and the steps performed to solve the problem. The PT returned to asking general questions about the student’s process. Thus, the PT did not get the student to reveal that they had made a mistake.

PT:

Okay. So from here, after you carried everything out, what did you do after that?

Student:

So after I traded 100, I saw that 3 was less than 5, so I need to make another trade

PT:

Okay. So you added this down?

Student:

Well, so, to make my trade here I took 10 from 180, which gave me 170, and I added 10 to 3 which gave me 13

This questioning elicited the steps of the student’s process for trading one 10 for 10 ones. The interaction concluded with the PT stating what they thought the student had done after trading.

PT:

Okay, and then you expanded and added it up at the end?

Student:

Well, I got these numbers by adding. So, like I added 400 plus 200 to get 600

PT:

Okay

The student confirmed that they added the numbers by place in expanded form. Then, the PT ended the interaction. This is an example of an interaction in which the PT did not uncover the student’s mistake. Additionally, as was common in our sample, this PT did not ask the student how they arrived at the final answer of 878.

This particular PT focused on eliciting the first three steps of the student’s process (expanding, comparing numbers in each place, and trading). As noted earlier, this was a common pattern. This case also illustrates a second pattern that emerged in performances related to the eliciting the student’s process: the majority of PTs filled in at least one step of the student’s process. In this case, the PT inferred that the student added the numbers by place and got the student to agree.

Eliciting the student’s understanding of the original process

We coded whether PTs elicited the student’s understanding of six key mathematical ideas underlying the process. Table 5 contains the six understandings that we coded, how the student expressed their understanding if pressed, the percentage of PTs who elicited each understanding, and the percentage of PTs who filled each understanding. The percentage of PTs eliciting each understanding ranged from 0 to 37%. The highest percentages of eliciting occurred around the operation in the problem (27%), why the student expanded (37%), and why the student traded (27%). When we looked across the set of ideas, we found that 33% of the PTs eliciting the student’s understanding of none of the core ideas, 33% of PTs elicited the student’s understanding of one idea, 30% of PTs elicited the student’s understanding of two ideas, and 3% elicited the student’s understanding of three ideas. We also saw that some PTs filled the student’s understanding of mathematical ideas underlying the process. The highest percentage of filling occurred around why the student needed to trade. Five of the PTs (17%) stated the idea, “when you do not have enough, you can get more by making trades” without first eliciting this information from the student. When we looked across the set of ideas, we found that 77% of PTs did not fill any understanding, 17% filled the student’s understanding of one idea, and 7% filled the student’s understanding of two ideas.

Table 5 Percentage of PTs who elicited and filled the student’s understanding
Full size table

The second most common understanding to elicit was why trading is needed. We next consider a case that illustrates a PT who elicited the student’s understanding of why trading is needed. This exchange occurred after the PT elicited that the student expanded numbers to make trading easier.

PT:

So what do you mean by trades? Do you mean like how you… what you did here making 180 into 170?

Student:

Right, right. So you need… when you’re subtracting, sometimes you don’t have enough and you need to do a trade

Here, the PT elicited that, according to the student’s understanding, a trade is needed in a subtraction problem when there is not enough to subtract.

Returning to the finding that 67% of the PTs elicited the student’s understanding of at least one idea underlying the process, we note that many PTs brought capabilities relevant for eliciting student understanding. However, their eliciting does not reveal discernment of which understandings are most important to focus on and/or are more relevant to subsequent instruction. For instance, the most commonly elicited idea (elicited by 37% of PTs) was that the student expands because it makes it easier to see and keep track of trades. This idea is relatively peripheral to the student’s work on this problem and does not offer much insight into the student’s reasoning about subtraction. More discerning eliciting might have focused on the student’s understanding of the operation or the reasonableness of the answer, ideas that are more directly related to the student’s mistake.

Eliciting the student’s mistake

We coded whether the PTs elicited the student’s mistake of adding instead of subtracting as well as whether PTs elicited the student’s understanding of why they made a mistake. We found three pathways in PTs’ performances. Forty-seven percent of PTs elicited the student’s realization that a mistake had been made. Twenty-percent of PTs pointed out or filled the mistake and got the student to confirm without first eliciting the mistake from the student. Thirty-three percent of PTs did not ask questions about the mistake. In other words, 67% of the PTs uncovered the mistake by either eliciting it or asking the student to confirm that they made a mistake; 33% did not learn about the mistake through questioning.

Eliciting the mistake from the student

We now turn to the 47% of PTs who uncovered the mistake by eliciting it from the student and examine how these PTs surfaced the mistake. These 14 PTs elicited the mistake in different ways. The most common way, used by 11 PTs, was to ask about the operation in the problem and to press on how the operation (subtraction) differed from the operation that the student used (addition). The student had used addition to expand the numbers; however, the student added the two expanded numbers rather than computing the difference. For example, one PT pointed to the subtraction sign in the original problem and asked why the student switched to adding 200 and 400 in the hundreds place.

PT:

What did you do after you made the trades that you needed?

Student:

Then I just added the… I added each one, so 200 plus 400 is 600, 170 plus 90 is 260. So I just added them up and down

PT:

And can you remember what the problem was asking you to do? In the very first place?

Student:

… [scratching head] Oh…it was asking me to subtract!

PT:

Yeah… that’s okay, though

Student:

So I should have subtracted

PT:

Yeah, subtracted

By asking the student what the problem was asking, the PT elicited that the student knew it is a subtraction problem and the student thought they had made a mistake.

Posing another problem to solve or asking the student to redo the original problem was another route to eliciting that the student had made a mistake. This approach revealed the mistake because the student profile specifies that the student should correctly apply the expand and trade method if prompted to solve another problem. Two PTs used this approach. One PT had the student resolve the original problem and then asked the student what differences they noticed between the original work and the revised work. The other PT posed the problem 13 − 5, which the student solved correctly and then asked why the student wrote that 13 − 5 equals 18 in the original problem. A third approach to eliciting the mistake was to ask about why the student had made the trades (to get enough to subtract). One PT leveraged this to ask why the student had added.

Pointing out the mistake to the student

Twenty percent of PTs uncovered the student’s mistake by pointing out the mistake themselves and getting the student to agree. Often, PTs made statements about what it appeared the student had done based on the written work. For example, one PT stated their impression that the student expanded and traded correctly and then added instead of subtracting. This exchange took place after the PT had elicited the steps of the student’s original process through the trading step.

PT:

So it looked like you separated them correctly, but then once you got to here… did you remember saying that we were working on a subtraction problem, correct?

Student:

Oh yeah

PT:

Yeah. So let’s work through this. Totally okay. So when you got to this step, I think what you did is you maybe added a little, instead of subtracting

Student:

Yeah. That was a mistake

PT:

Totally okay. No worries

While this PT referenced a previous question about the operation involved in the problem, the idea that the student mistakenly added instead of subtracted was introduced by the PT, not the student. The student merely confirmed what the PT had filled in. We see this “filling” approach to uncovering the mistake as qualitatively distinct from eliciting the mistake by asking questions.

Did not learn about the student’s mistake

One third of the PTs did not learn about the student’s mistake during the simulated interaction. However, we know that these PTs were aware that the student’s answer was incorrect because all PTs articulated that the student arrived at an incorrect answer during the follow-up interview. The distinction here is that these 10 PTs did not get the student to reveal or confirm that they had made a mistake during the teaching simulation. These PTs likely inferred the student’s mistake from the written work and chose not to ask questions about it.

Following up after the student revealed they made a mistake

We now consider the larger subset of PTs (67%) who learned that the student made a mistake by either eliciting or asking the student to confirm that they made a mistake. There are 20 PTs in this group. We begin by considering the extent to which they elicited why the student believed that they had made a mistake. Then, we turn to the extent to which they elicited a revised process.

Following up about why the mistake was made

There were three ways that PTs’ followed up about why the mistake was made: (1) asking no questions about why the mistake was made; (2) asking questions about why the mistake was made; and (3) stating a reason why the student might have made the mistake without first eliciting it from the student. We next discuss each of these ways of following up.

After learning that the student made a mistake, 12 of the 20 PTs did not ask any further questions about the mistake. Some PTs moved directly to eliciting a revised process. For example, one PT asked questions to elicit the student’s process, including that the student mistakenly added instead of subtracting (see transcript excerpt below). Other PTs indicated that they had no additional questions.

PT:

And so, what did you do… what did you do once everything was figured out?

Student:

400 plus 200 is 600

PT:

Are we adding here?

Student:

[Pause, looking at work]

PT:

Are we adding 400 plus 200, or are we subtracting? Like we… from the overall problem

Student:

Oh… I might have made a mistake

Once the student indicated that they might have made a mistake, the PT asked the student to revise their solution without posing any further questions about the mistake.

Of the 8 PTs who did follow up about the mistake, 5 filled in student thinking, or made statements based on their own inferences about how and/or why the student made the mistake and got the student to agree. For example, one PT elicited that the student had made a mistake and then shared their interpretation of how and why the student got confused.

PT:

So if you did… [writes problem] this, then what is the answer?

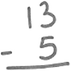
Student:

Eight

PT:

Eight. So here on your problem you have 18. Do you know why… you did 18 instead of 8?

Student:

Uh… I must have added instead of subtracted

PT:

Yeah, so it looks like you did that for all…

Student:

I should have been subtracting, yeah

PT:

However, you did remember to carry over the values. So you were confused between the subtraction and the addition because, when you expanded… possibly this addition symbol threw you off

Student:

Oh

PT:

And made you think that you were adding instead of subtracting

Student:

Uh huh

The remaining 3 PTs asked questions to learn about how and/or why the mistake was made. For example, upon hearing that the student had made a mistake, one PT followed up with a “how” question.

PT:

Did you do anything with the subtraction sign?

Student:

Um… I think I made a mistake actually

PT:

You did? How do you think… How did you make a mistake?

Student:

So I think I was seeing all of these addition signs and I forgot that I was subtracting

PT:

Oh, okay. That makes sense

However, this type of eliciting around the mistake was not common.

Following up about revising the process

Fifteen of the PTs who uncovered the mistake elicited some or all of the revised process from the student. Sometimes this included asking about all of the steps in the process again. For example, one PT elicited that the student made a mistake and then shifted focus to the revised process.

Student:

Oh… I might have made a mistake

PT:

It’s okay. We can start over. So instead of adding, what could we do with the 400? Is it 400 plus 200 now? Or is it 400 minus 200 now?

Student:

400 minus 200

PT:

Good. And then, so, what would that be?

Student:

200

PT:

Would you like to write that down? [hands student a marker]

Student:

Sure.[writes]

PT:

Alright. So. And then, what is the tens place?

Student:

170 take away 90…

PT:

You can, you can write scratch paper if you need it

Student:

That’s 80

PT:

Okay. And then… what is 13 minus 5? Is it 13 plus 5 or 13 minus 5?

Student:

Oh it’s 13 minus 5. And that’s 8

PT:

Right, so that’s 8. Alright, great. Okay, wait, just a second… make sure that’s right. Yeah, okay. And so, you added all these up? Why?

Student:

Well ‘cause you… I need to add them up to know what the final answer is

At the end of the interaction, the PT had gotten the student to talk through their revised process. However, this PT did not return to the mistake and did not learn about why the mistake was made.

Other times PTs focused the interaction on redoing the step where the student had made the mistake. For example, one PT asked the student what they would do differently if they were to solve the same problem again. In 10 of the 20 cases, the PTs pursued a line of questioning in which they asked the student to revise their final answer. PTs were more likely to elicit the student’s revised process than to follow up on how or why the mistake was made.

What can be learned from the capabilities that novices bring?

Responsible instruction builds on the knowledge and capabilities that learners bring. The shift to practice-based teacher education requires that the field develop new ways of learning about the knowledge and capabilities relevant to practices of teaching that novices are bringing to teacher preparation. This study has both empirical and methodological contributions.

This study contributes empirically by revealing the capabilities that PTs might bring to teacher education that are relevant for eliciting student thinking in the context in which a student is using an alternative algorithm and makes a mistake. The mistake is a type of bookkeeping error. If pressed about the reasoning behind their thinking, the student recognizes that they have made a mistake. The data illustrate the moves relevant to eliciting a student’s mathematical thinking when a student has made a mistake that one group of PTs brought to teacher education. For instance, we learned that these PTs were more fluent with eliciting procedural aspects of the student’s thinking (e.g., What did you do next?) than conceptual aspects (e.g., Why did you do that?). Most of our PTs (70–90%) were able to elicit the first three steps in the student’s original process during the simulation. Sixty-seven percent of PTs elicited the student’s understanding of one or more ideas behind the process. However, these PTs’ eliciting of the student’s understanding was scattered across key ideas. Many PTs only learned why the student likes to expand numbers.

Student mistakes can provide fruitful learning opportunities for teachers to learn mathematics, patterns of student thinking, and to build relationships with students. Considering interactions around a mistake, one of the key pieces of information a teacher can uncover is why a student made a mistake in the first place. At the start of their teacher education program, these PTs focused more on eliciting the revised method and/or solution than the reasoning behind the mistake. It is possible that some PTs interpreted the instructions not to teach the student to mean that they could not ask the student to revise their thinking. However, this does not explain why they did not ask about the mistake itself, including why the student made the mistake. Moreover, such an interpretation of the instructions may signal a need to broaden PTs’ conceptions of what eliciting student thinking can entail. It is also possible that PTs may have thought that the mistake was obvious. In other words, the mistake did not provoke a question for them to wonder about (Shaughnessy et al. 2018) and the PTs did not ask a question as a result. Echoing Stockero and Van Zoest’s (2013) observation that PTs often fail to recognize and act on “Pivotal Teaching Moments” in whole class mathematics discussions, these PTs missed an important eliciting opportunity during their interaction with the student.

Such findings can be considered in terms of capabilities brought by PTs that could be built upon in teacher education, capabilities that need to be learned, and capabilities that need to be unlearned (Shaughnessy and Boerst 2018a). It is possible to see capabilities in more than one category. Concerning capabilities that could be built upon and leveraged in the teacher education program, these PTs were able to ask questions to elicit part of the student’s process. In other words, they brought capabilities to ask questions to elicit the student’s process. However, only 53% of PTs elicited the step that contained the mistake. This finding is consistent with studies showing that teachers focus disproportionately on correct student thinking (Bray 2011; Santagata 2005; Silver et al. 2005). In the context of teacher education, we could work with these PTs to learn to continue to ask questions about students’ full processes and to ask questions even (or especially) when steps include mistakes. These PTs also brought some capabilities with posing questions directed at the student’s understanding. At the same time, new learning is required by these PTs. While PTs did often ask a question about the student’s understanding, their foci were scattered. In other words, these PTs would benefit from work on more carefully determining foci for eliciting student thinking to learn about student understandings. In addition, these PTs need to learn how to ask questions that focus on why a student made a mistake. This likely involves constructing a new conception of one’s role as a teacher of mathematics as someone responsible for seeking detailed insights into students’ thinking.

Unlearning is also required by some of these PTs. We use “unlearning” to convey that some of the moves employed by PTs suggest that some of the capabilities brought to teacher preparation by novices may undermine the work that teachers need to do (Shaughnessy and Boerst 2018a). For example, some PTs need to unlearn the practice of stating assumptions and asking for confirmation and instead learn to ask questions that elicit steps of the process and/or understandings from the student. These PTs also appeared to need to unlearn the idea that getting a student to arrive at a correct answer is of the utmost importance in teaching mathematics. This area for unlearning is closely connected to new learning about the importance of asking questions that focus on why a student makes a mistake. Upon uncovering that the student made a mistake, many of these PTs asked the student to correct their work without any attention to why the mistake was made, which emphasizes getting a correct answer over understanding the student’s mathematical reasoning. Learning to ask questions about why a mistake was made, including understandings behind the mistake, can begin to challenge the pervasive idea that mathematics is simply right or wrong and can support novices in building upon information elicited from students in subsequent instruction. As we have argued elsewhere (Shaughnessy and Boerst 2018a; Boerst et al. 2020), PTs may be bringing capabilities to teacher education that are productive and useful in everyday life. However, these same capabilities might not be well aligned with professional practice.

In sum, the data provide a portrait of this group of novice teachers, which can be used by the teacher educators working with these novices. Other teacher educators may also find it useful to look for and consider the relevance of the patterns we have identified in their own efforts to support PTs’ eliciting work.

These empirical contributions suggest several directions for continuing research. First, the PTs in this study were in their first week of a teacher education program. In what ways do their capabilities with eliciting student thinking in the context in which a student has made a mistake develop over time? We are interested in comparing the performances of these PTs with their performances at the mid-point and end of the teacher education program. Second, the assessment itself involved a mistake where the student was using a “nonstandard” approach to solve the problem. Anecdotally, we have reason to think that some PTs were discounting the student’s reasoning because they believed that the student should be using a different method to solve the subtraction problem. A future study could compare capabilities in eliciting around a mistake in two different contexts, a “standard” algorithm and an “alternative” algorithm. Third, the teaching simulation is an approximation of practice that reduces the complexity of interacting with students in a classroom. Therefore, future research could explore the relationship between PTs’ eliciting work in the simulation and in live classroom settings.

Methodologically, the study builds on prior uses of teaching simulations by showing that it is possible to design and use a simulation where the student will change their mind if asked particular questions. This approach enables us to gather data on PTs’ eliciting capabilities within a particular recurrent problem of practice. We believe that this problem of practice, eliciting when a student has made a mistake, is a crucial one to work on in teacher education. Capable teachers can learn about the mistakes that children make and the reasoning behind those mistakes and use the information to design learning experiences that are responsive to current understandings. As this study shows, novices may never surface that a student has made a mistake or why a student has made a mistake and may thereby run the risk of incorrectly labeling a child as needing remediation. Thus, teacher education programs need to track on novices’ developing capabilities in this context.