The influence of spin state of the Cr ions on the structural and magnetic behavior of orthorhombic LaFe_1−xCr_xO₃ Perovskites (0.0<x<0.5)

Abstract

Herein, we report, for the first time, the influence of the state of spin of the Cr³⁺ ions on the structure and magnetic behavior of LaFe_1−xCr_xO₃ (0.0 < x < 0.5) perovskite crystal structures to improve their magnetic properties for memory storage and magneto-optical application potential. A series of LaFe_1−xCr_xO₃ (0.0 < x < 0.5) nanocrystals was prepared using the citrate-nitrate auto-combustion route. The influence of the Cr³⁺ ions on the structure and morphology of the LaFe_1−xCr_xO₃ nanostructures was emphasized using X-ray diffraction (XRD), high-resolution transmission electron microscopy (HRTEM), the selected area of electron diffraction (SAED), and scanning electron microscopy (SEM). The results revealed that the inclusion of the Cr³⁺ ions into the Fe³⁺ sites leads to an increase in the crystallite size of the LaFe_1−xCr_xO₃ (0.0 < x < 0.5) nanocrystals, from 16.12 to 57.29 nm, to preserve their orthorhombic crystal symmetry. The phase stability and the electron density mapping of the prepared orthoferrite nanocrystals were verified using the Goldschmidt tolerance factor and Rietveld refinement. The magnetic properties were evaluated and discussed based on Kanamori–Goodenough (KG) regulations and Heisenberg Hamiltonian notation. The results showed that the inclusion of the 20 mol% of Cr³⁺ ions in the Fe sites results in an enhancement of the magnetic parameters. The enhancement of the magnetic behavior was argued to the tendency of the Cr³⁺ ions to be in the high spin state when included in the Fe³⁺ ions site. This improvement in the magnetic performance of the LaFe_1−xCr_xO₃ (x = 0.2) nanocrystals will open a new avenue for using this nanomagnetic material in the fields of memory storage and magneto-optical devices.

1 Introduction

Rare-earth orthoferrites with a typical formula of RFe_1−x M_xO₃ with (R = Pr, Nd, Dy, La, Eu, Gd, Tb, Sm, Er, etc.) and (M = transition metals as Mn, Cr, Zn, etc.). These rare-earth elements make a significant contribution to the ferrites’ net magnetic response. These classes of metal oxide nanoparticles have attracted great attention due to their multi-functionalities and their significant magnetic properties [1,2,3,4,5]. As a result, these perovskites have promising characteristics for applications such as gas separation, memory storage devices, fuel cells, gas sensing, magneto-optical devices, and electromagnetic equipment, as well as modern electronic technology [6,7,8,9,10]. It is commonly recognized that combining several compositions with superior electrical properties results in new composite materials, which have grabbed the curiosity of researchers in recent years. The addition of a second phase can significantly enhance the resulting composite material’s electrical characteristics [11, 12].

LaFeO₃ (LFO), one of the key rare-earth orthoferrites, has been widely reported for a broad range of industrial applications, including solid oxide fuel cells, sensors, and environmental catalysts [13], among others. LFO is a rare-earth orthoferrite that crystallizes in an orthorhombic structure with pbnm (No.62) symmetry [14], with a great value of Neel temperature of 750 K, and an antiferromagnetic (AFM) axis oriented along the crystallographic a-axis [9, 10, 15]. As K. Rachid et al. [1] point out, the synthesis process used has a considerable influence on characteristics and the composition’s structure. Many chemical methods have been used to synthesize LFO and related perovskite compositions, including sol–gel, hydrothermal, microwave-assisted, co-precipitation, citrate-gel auto-combustion approach, mechanochemical synthesis [16,17,18,19,20,21,22,23].

First, A. Paul Selvadurai et al. [15] demonstrated the LFO multiferroic characteristics, studied the interaction of (AFM/FM), and reported irreversibility in the FCC–ZFC curve. Second, according to the Goodenough-Kanamori hypothesis, Cr³⁺ is the optimum substitute element for increasing the magnetization of LaFeO₃ since Fe³⁺ and Cr³⁺ arranged at the octahedral site as Fe³⁺(d₅)–O²⁻–Cr³⁺(d₃) would have improved the magnetism due to the super exchange interaction [24]. Yan Chen et al. discovered that substituting Cr³⁺ ions for Fe³⁺ ions increase the proportional fraction of Fe³⁺–O²⁻–Cr³⁺ FM super exchange interaction, resulting in a maximum magnetic moment at x = 0.5 in their research of magnetic characteristics of LaFe_1−xCr_xO₃ (0 > x > 1). Even though iron and chromium ions were being randomly allocated at the Fe site, an improved saturation magnetization of 0.21 B/f.u [25] was observed and reported later [26,27,28].

Y.M. Abbas et al. used the sol–gel auto-combustion route to synthesize the orthoferrite system La_1−xY_xFeO₃, which exhibits a canted antiferromagnet and shows a weak ferromagnetism at 300 K [29], and they argued that the contribution of magnetic attitude of the synthesized compositions reflected differences in magnetic moments of Fe³⁺ (5 µB) and Fe^+ 2 ions (4 µB). With rising Y³⁺-content, the effective moment showed a significant decrease.

As a result, Cr³⁺ substitution in LaFe_1−xCr_xO₃ could result in intriguing magnetic and electrical properties. The layered development of LaCrO₃–LaFeO₃ using the molecular beam epitaxy (MBE) approach corroborated the increase in magnetization [30].

Herein, we report for the first time the influence of the state of spin of the Cr³⁺ ions on the structure and magnetic behavior of LaFe_1−xCr_xO₃ (0.1 < x < 0.5) perovskite crystal structures. The inclusion of the Cr³⁺ ions in the Fe sites results in a dramatic change in the Goldschmidt tolerance factor and a change in the dimensions of the formed crystallites. This change gave rise to an enhancement of the magnetic parameters. The enhancement of the magnetic behavior was argued to the tendency of the Cr³⁺ ions to be in the high spin state when included in the Fe³⁺ ions site.

2 Experimental details

Numerous methods were used for synthesis of orthoferrites, including sol–gel, hydrothermal, microwave-assisted, co-precipitation, citrate-gel auto-combustion approach, and mechanochemical synthesis [16,17,18,19,20,21,22,23]. The orthoferrite system LaFe_1−xCr_xO₃ with (x = 0.0, 0.1, 0.2, 0.3, 0.4, and 0.5) were synthesized via sol–gel auto-combustion route, and citrate acid is used as a fuel. Various steps were used as described in Fig. 1. The starting raw materials for synthesis are La(NO₃)₃.6H₂O (Alfa Aesar, purity 99.99%), Fe(NO₃)₃.9H₂O (Alfa Aesar, purity 99.98%), Cr(NO₃)₃.9H₂O (Alfa Aesar, purity 99.90%), and citric acid monohydrate C₆H₈O₇.H₂O (Alfa Aesar, purity 99.50%). Separately, one hour was spent dissolving the metal nitrates in distilled water before they were mixed stoichiometrically with constant stirring. The ratio of nitrates to fuel was kept constant (1:1). A temperature range of 353–363 K was used to dissolve the solution while being stirred continuously at 1700 rpm, and the pH was regulated by adding the right quantity of (NH₃.OH 33.3%) aqueous solution drop by drop during the stirring operation to raise the PH to ~ 7. The dried gel was decomposed into the powder at 573 K in an air environment, and then a vigorous thermochemical combustion process produced the deep brown powder. By increasing the amount of chromium, the blackness of the powder rose. The resulting power perovskites were grinded in an agate mortar and calcinated in open air at 1123 K for 6 h.

Fig. 1

The flow chart of sol–gel auto-combustion synthesis of powder LaFe_1−xCr_xO₃.

$${\text{La}}\left( {{\text{NO}}_{{\text{3}}} } \right)_{{\text{3}}} \cdot{\text{6H}}_{{\text{2}}} {\text{O}}\, + \,{\text{Fe}}\left( {{\text{NO}}_{{\text{3}}} } \right)_{{\text{3}}} \cdot{\text{9H}}_{{\text{2}}} {\text{O}}\, + \,{\text{C}}_{{\text{6}}} {\text{H}}_{{\text{8}}} {\text{O}}_{{\text{7}}} \cdot{\text{H}}_{{\text{2}}} {\text{O}}\, + \,{\text{4NH}}_{{\text{3}}} \cdot{\text{H}}_{{\text{2}}} {\text{O}}~\xrightarrow{{{\text{pH}} = 7}}(monophase\,{\mathbf{LaFeO}}_{{\mathbf{3}}} )\, + \,{\text{6CO}}_{{\text{2}}} \uparrow \, + \,{\text{5N}}_{{\text{2}}} \uparrow \, + \,{\text{3}}0{\text{H}}_{{\text{2}}} {\text{O}} \uparrow.$$

(1)

All the synthesized perovskites were investigated by (XRD, X’Pert pro PANalytical MRD instrument) using Cu-K_α irradiation (λ = 1.54056 Å) for phase identification and structure. The Rietveld approach was employed to determine the refined crystallographic parameters such as unit cell dimensions, electron density, breadth, atomic coordinates, thermal parameters, microstructural parameters, atomic site occupancies, etc. for each perovskite. The FullProf package was used to perform the structural refinement of XRD patterns for the prepared samples. The refinement process was performed on the patterns with a 2° (2θ)/min counting rate per step. The refining approaches for all the perovskites under study began with crystallographic data from LFO [31]. In the structural analysis, the peak shapes for distinct samples were illustrated using an asymmetric “Thompson-Cox-Hastings Pseudo-Voigt function with axial divergence symmetry”, the size/strain broadening caused by the sample contribution might be calculated based on this. Using the GFourier tool (FullProf Suite Package), the electron density mapping (EDM) within the unit cell was estimated and visualized. Several literary works [32,33,34,35,36,37,38,39] have detailed descriptions of the mathematical methodologies used in the Rietveld approach. The crystallite size and shape of the calcinated powder were investigated using HRTEM, JEOI-JEM 2100 equipment (National Research Center (NRC), Egypt). The materials’ morphology and composition analysis were studied using Quanta FEG-250 SEM-EDX. Using a VSM, the magnetization (M) was measured over a magnetic field (H) range of (0–20kOe) (Lakeshore 7310, ACR, El-Dokki, Egypt).

3 Result and discussion

3.1 Structure analysis

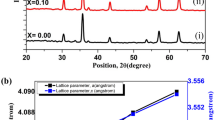
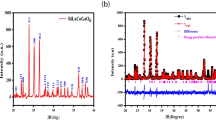
The crystallography of the prepared samples was evaluated using conventional XRD. Figure 2 displays the XRD spectrum for the LaFe_1−xCr_xO₃ perovskite group. The diffraction patterns were refined using Rietveld approach, which yielded peaks for the (101), (121), (220), (202), (240), (242), and (204) planes, correlated with (JCPDS: No. 88–0641), of which a negative x/a site coordinate value yields from the symmetric evolution of Pnma to Pbnm [40], The XRD measurements and Rietveld analysis confirmed that there are no secondary phases that have been formed. It also confirms that the prepared compositions formed a monophase inside the detection limit of XRD. According to Selvadurai et al. [15], the shift of diffraction peaks to higher 2θ with increasing Cr doping is attributable to the less significant ionic radius of the Cr^+ 3 cation compared to the Fa^+ 3, which they attribute to the absence of any secondary phases in the starting materials [13].

Fig. 2

XRD patterns of Perovskites LaFe_1−xCr_xO₃ (X = 0.0, 0.1, 0.2, 0.3, 0.4, and 0.5)

The Goldschmidt’s tolerance factor is an indicator for crystal structure stability and deformation. Goldschmidt tolerance factor (t) of the perovskites LaFe_1−xCr_xO₃ is a dimensionless quantity computed using the ionic radii ratio and is expressed as follows [3, 41]:

$$t\, = \,\frac{{{\text{R}}_{{\text{O}}} + ~{\text{R}}_{{{\text{La}}}} }}{{\sqrt 2 ~({\text{R}}_{{\text{O}}} + ~(\left( {1 - x} \right)~{\text{R}}_{{{\text{Fe~}}}} + ~{\text{x}}~{\text{R}}_{{{\text{Cr}}}} )}},$$

(2)

where ${\text{R}}_{\text{La}}$, ${\text{R}}_{\text{C}\text{r}}$, ${\text{R}}_{\text{O}}$, and ${\text{R}}_{\text{Fe}}$ are the ionic radii of the La, Cr, O and Fe ions, sequentially.

The tolerance factor (t) is a geometric factor describing the size difference that occurs when the cations of A-site are too small to occupy the space in the 3-dimensional octahedral [BO₆] network. If the A-site cation is less than the ideal value, t will be less than unity.

Therefore, in attempting to occupy space, the [BO₆] octahedra will tilt. For an ideal cubic structure (t = 1), the perovskite structure is steady when (0.75 < t < 1.0) and cubic when (t > 0.95) [42]. The orthorhombic symmetry of the perovskites is assured by (t) values in the range of (0.85 < t < 0.95) [3, 43]. Lanthanum and chromium ions have ionic radii of (1.216 Å) and (0.615 Å) on a 9-fold and 6-fold coordinations, respectively. On a 6-fold symmetry of octahedral [FeO₆], iron and oxygen have values of (0.645 Å) and (1.400 Å), respectively. Because of the variation of both Fe^+ 3 and Cr^+ 3 ionic radii, which causes the reduction in the cell volume. The (t) values increase with rising chromium concentration at the expense of iron ions, as displayed in Fig. 3. The increase in deformation was caused by tilting of the octahedron [FeO₆] due to a decrease in R_B cation size. So, when t < 1, the Fe–O–Fe ≠ 180° change in the out of plane Fe–O bonds, which gives rise to the tilting mode [26, 30].

Fig. 3

The variation of the tolerance factor with Cr³⁺ content (x)

Figure 4a–f shows the Rietveld refinement of XRD patterns for the perovskite system LaFe_1−xCr_xO₃. We refined the lattice parameters for all the compositions, and Table 1 summarizes the results. Since the Cr³⁺ cation is smaller than the Fe³⁺ cation, the substitution with Cr results in a reduction of cell volume V, which is an expected result. As the chromium substitution increases, the lattice parameters a, b, and c fall slightly, suggesting a considerable decrease in system volume, which causes lattice geometry distortion. Figure 5 illustrates the variation of cell volume (V) and grain size (D) as a function of Cr concentration. The lattice parameters of the prepared perovskites coincide with previously published values [25, 44]. The decreases in crystallite size with increasing the amount of Cr³⁺ ions may be attributed to the substitution of Fe³⁺ ions with large ionic radius by the Cr³⁺ ions with small ionic radius and/or the inclusion of Cr³⁺ ions may cause the formation of oxygen vacancies. Both of these two reasons give rise to the decrease in crystallite size [44, 45].

Fig. 4

Rietveld refinement of XRD patterns of Perovskites a LaFeO₃ b LaFe_0.9Cr_0.1O₃ c LaFe_0.8Cr_0.2O₃ d LaFe_0.7Cr_0.3O₃ e LaFe_0.6Cr_0.4O₃ f LaFe_0.5Cr_0.5O₃

Table 1 Refined structural parameters, atomic positions, reliability factors, and calculated mean crystallite size (D_XRD) of LaFe_1-xCr_xO₃ (0.0 < x < 0.5) perovskites obtained by the Rietveld method in space group of the pbnm

Fig. 5

Variation of Crystallite size (D) and volume of unit cell (V) as a function of Cr substitution (x) for perovskite system LaFe_1−xCr_xO₃, (x = 0.0, 0.1, 0.2, 0.3, 0.4, and 0.5)

For the perovskites under investigation, the particle size (D_XRD), and micro-strain were determined using the Williamson–Hall (W–H) plot, and the estimated particle size values are listed in Table 1. Equation 3 correlates strain-induced broadening caused by crystal defects and distortion [29].

$$\varepsilon \, = \,\frac{{\beta _{S} }}{{\tan \,\theta }}.$$

(3)

According to the several methodologies, the overall integral breadth of a Bragg peak is made up of the additive components of the crystallite size and micro-strain broadening. The distinction of size and strain broadening in the (W–H) analysis was based on the various θ dependencies of both effects, as shown in the following equations [29]:

$${{\upbeta }}_{\text{h}\text{k}\text{l}}={{\upbeta }}_{\text{D}}+{{\upbeta }}_{{\upepsilon }}=\frac{\text{K}{\uplambda }}{\text{D} \text{c}\text{o}\text{s}{\uptheta }}+4\text{t}\text{a}\text{n}{\uptheta },$$

(4)

$${{\upbeta }}_{\text{h}\text{k}\text{l}}\text{c}\text{o}\text{s}{\uptheta }=\frac{\text{K}{\uplambda }}{\text{D} }+4\epsilon\text{s}\text{i}\text{n}{\uptheta }.$$

(5)

All of the material’s properties should be very independent of the direction in which they are examined because the strain is expected to be isotropic. For the refined diffraction data of LaFe_1−xCr_xO₃ powder, the term (β_hkl cosθ) was drawn as a function of (4sinθ). W–H plots for the refined XRD data show the strain term computed from the slope (ɛ) of the fitted line and the size part calculated from the line cutoff (Kλ/D) as presented in Fig. 6. Based on the W–H plot and Rietveld refinement of the XRD data for the prepared perovskites, Table 1 displays the calculated mean particle size, which ranged from 16.2 to 57.29 nm. A GFourier (FullProf software package) is employed to compute and display the electron density $\rho$($\text{x},\text{y},\text{z}$) as a result of incident X-ray scattering on the unit cell. These estimations use the Fourier method and the fast Fourier transform (FFT). Based on the FFT in the fitted XRD data, Eq. 6 is used to estimate the electron density (ED) [29].

Fig. 6

Williamson–Hall Plot for the refined XRD data of Perovskites a LaFeO₃, b LaFe_0.8Cr_0.2O₃, c LaFe_0.7Cr_0.3O₃, and d LaFe_0.5Cr_0.5O₃.

$$\rho (\text{x},\text{y},\text{z})=\frac{1}{\text{V}}{\sum }_{\text{h}\text{k}\text{l}}\left|{\text{F}}_{\left(\text{h}\text{k}\text{l}\right)}\right|{\text{e}}^{-2{\uppi }\text{i}({\text{h}}_{\text{x}}+{\text{k}}_{\text{y}}+{\text{l}}_{\text{z}}-{\alpha }_{\left(hkl\right)})},$$

(6)

where $\rho (\text{x},\text{y},\text{z})$ is the electron density at a position $\text{x},\text{y},\text{z}$ in a unit cell volume V, $\left|{\text{F}}_{\left(\text{h}\text{k}\text{l}\right)}\right|$ is the structure factor magnitude, and ${\alpha }_{\left(hkl\right)}$ corresponds to the phase angle of each Bragg peak.

Figure 7 shows 3D maps for perovskites LaFe_1−xCr_xO₃ with (x = 0.0, 0.2, and 0.5). Thicker ED contours indicate the existence of a heavy element among the unit cell’s fundamental elements of the prepared orthoferrites. In contrast to the colored areas, which range in color from red to violet-brown, the contour line of zero-level density is shown in black, depicting rising ED levels around the La cation. The positions of the several oxygen atoms in the unit cell show relatively substantial displacements compared to the FelCr and La positions, where significant positive peaks belong to the 4c positions.

Fig. 7

3D Electron density map of individual atoms on the yz plane in the unit cell of Perovskites a LaFeO₃ b LaFe_0.8Cr_0.2O₃ c LaFe_0.5Cr_0.5O₃, Fe³⁺|Cr³⁺ peaks are obviously located on 4b sites, and La³⁺ peaks located on 4c sites. 

The cations FelCr and La are positioned at (0.0, 0.0, 0.5) and (0.028, 0.250, 0.993), respectively, according to the Rietveld refinement results. Figure 7 clearly illustrates the variation in scattering density between the O²⁻ anion, La, and FelCr cations. We shall be able to understand the magnetic properties of the multiferroic system due to this variability in the ED in the crystal lattice.

3.2 TEM analysis

HRTEM imaging of the structure was performed to provide additional support for the formation of nanoparticles, such as particle shape and size for perovskite LaFe_1−xCr_xO₃ (x = 0.0, 0.1, 0.2, 0.3, 0.4, and 0.5) nanocrystallites. According to XRD results, the single-phase nanocrystalline material, as revealed in Fig. 2, is composed of many tiny single crystals.

As displayed in Fig. 8, HRTEM images confirmed that the particles were an agglomeration of several quasi-spherical particles that had quietly accumulated, and the single-direction configuration of the lattice fringes provided further evidence of the perovskites’ polycrystalline nature. In TEM images, particle agglomeration is responsible for the distinct values of crystallite size obtained by TEM and XRD. The estimation of separate, unagglomerated nanoparticles (NPs) is simple. When NPs are attached together or have an irregular shape, the precise size distribution can be more difficult to measure. The mean particle size calculated from TEM micrographs was approximately 57 nm for LaFeO₃ and decreased to 17 nm for LaFe_0.6Cr_0.4O₃, which is very well consistent with XRD results and W–H calculations. According to the HRTEM image of the NPs-suggested part, lattice planes (101) and (121), respectively, have interplanar spacings of 0.39 and 0.27 nm for samples LaFeO₃ and LaFe_0.7Cr_0.3O₃, as seen in Fig. 9 and verifying the XRD results. The main diffraction zones correspond to (101), (121), (220), (202), (242), and (204) of orthorhombic nanocrystalline orthoferrites (SG: Pnma), with no impure phase spots, and agree with XRD results. The Selected Area Electron Diffraction (SAED) patterns of perovskite LaFe_0.5Cr_0.5O₃ were indexed using the CSpot software, as illustrated in Fig. 10. Table 2 summarizes and compares the values of such interplanar spacing in sample LaFe_0.5Cr_0.5O₃ as revealed by XRD and TEM investigations. The intensity of the rings was related to the number of diffracting particles, which was determined by the size of the selected area. For polycrystalline materials, large selected areas are necessary to obtain good diffraction patterns.

Fig. 8

HRTEM micrographs, corresponding SAED patterns, and size histograms of a LaFeO₃, b LaFe_0.8Cr_0.2O₃, c LaFe_0.6Cr_0.4O₃, d LaFe_0.5Cr_0.5O₃

Fig. 9

The measured interplanar spacing for perovskites a LaFeO₃, b LaFe_0.7Cr_0.3O₃

Fig. 10

Indexing of SAED patterns for the perovskite LaFe_0.5Cr_0.5O₃, using CSpot software

Table 2 The d-spacing for the diffraction peaks (101), (121), (220), (202), (242), and (204) of the trimetallic composition LaFe_0.5 Cr_0.5O₃ obtained by XRD and HRTEM.

3.3 SEM-EDX characterization

Scanning electron microscopy with energy-dispersive X-ray spectroscopy (SEM/EDX) was used to examine the surface morphologies of the calcinated samples. The SEM images clearly show the formation of agglomerated, nonuniform spherical grains. As shown in Fig. 11, raising the Cr substitution reduces grain size and increases the agglomeration of NPs.

Fig. 11

SEM-EDX images of the prepared orthoferrites a as-prepared LaFeO₃, b LaFe_0.7Cr_0.3O₃, (Calcinated at 800 ^oC) c LaFe_0.5Cr_0.5O₃ (Calcinated at 800 ^oC)

As shown in Fig. 11, the particle configurations of perovskites LaFe_0.7Cr_0.3O₃ and LaFe_0.5Cr_0.5O₃ are almost the same and likely to become spherical after 5 h of calcination at 800 ^oC, compared with the as-prepared LaFeO₃, these findings suggest that LaFe_1−xCr_xO₃ nanostructures’ morphology is greatly influenced by the calcination temperature. The mean grain diameter was approximately 57 nm for pure LFO and reduced to 37.4 nm for LaFe_0.5Cr_0.5O₃. Figure 11a–c illustrates an EDX elemental analysis of the perovskites LaFe_1−xCr_xO₃ (x = 0.0, 0.3, and 0.5). All peaks are assigned to the spectrum arising from the Fe, La, and O elements of the prepared perovskites. This implies the high purity of the prepared samples. The concentrations of these elements are presented in tables set in Fig. 11a–c. It is noted that the concentrations of these elements agree with the calculated amounts of the elements during preparation, confirming the stoichiometry of the prepared samples owing to the quality of the synthetic recipe compared to the other methods [46]. It is also noted that the inclusion of Cr³⁺ ions into Fe sites leads to a slight decrease of the oxygen amount, implying that there is the possibility of the formation of oxygen vacancies [47].

3.4 Magnetic measurements

Based on the M(H) curves, the magnetic parameters were calculated, including saturation magnetization (M_s), remnant magnetization (M_r), retentivity, and coercive field (H_c). The magnetic hysteresis over the M(H) loop for all the synthesized compositions was characterized at 300 K by using VSM in a field range of ± 20 kOe, as illustrated in Fig. 12. The magnetic susceptibility (χ) measurements of the prepared powder were determined by a VSM inside a field of 1.55 kOe from 400 to 900 K. The hysteresis behavior of samples, as shown in Fig. 12, indicates a weak FM, and this could be due to many reasons. The first possible reason may be due to the oxygen vacancy effect, which may decrease the exchange interaction. These oxygen vacancies show a negative indirect exchange according to Kanamori–Goodenough (KG) empirical rule [48]. Therefore, these oxygen vacancies may lead to the formation of a weak magnetic state, such as spin glass [49, 50].

Fig. 12

Room-temperature M(H) curves of LaFe_1−xCr_xO₃ (x = 0.0, 0.1, 0.2, 0.3, 0.4, and 0.5)

The superexchange (SE) interaction is the second reason. In accordance with Kanamori–Goodenough (KG) regulations, Fe³⁺–O^2-–Fe³⁺ and Cr³⁺–O^2-–Cr³⁺ SE interactions are antiferromagnetic [51, 24], whereas Cr³⁺–O^2-–Fe³⁺ is expected to be ferromagnetic. Previously, there has been no evidence of strong FM in bulk form of Cr-doped LaFe_1−xCr_xO₃, as noted in LaCrO₃–LaFeO₃ layered growth [30]. Because Cr substitutions prefer the Cr–Cr coupling on substitution in the host metal cation, as well as the variation of Cr cation in the host site, showing up a weak FM [52]. These Cr³⁺–Cr³⁺ coupling behaviors were detected in LaFe_0.8Cr_0.2O₃ and LaFe_0.7Cr_0.3O₃. The third reason for weak FM behavior could be attributable to a cluster or an impurity phase coexisting with the first two reasons [53]. As a result, the room-temperature FM in the perovskites under investigation can be explained by the SE interaction of Fe³⁺–O^2-–Fe³⁺ ions, which results in the FM shell model at a particle’s surface because of irregular spins and the core of AFM particles as a result of ordering spins [54, 55]. With decreasing crystallite size and the high surface area of these Fe³⁺ ions, there was an increase in the disordered spin volume fraction relative to the ordered spin volume fraction. In addition, this attitude has also been discovered in other types of perovskites. A. Paul Blessington Selvadurai et al. [15] reported a value close to the M_r and H_c of our samples with (x = 0.0, 0.1), because of the well-grown nanocrystallites, surface disorder is reduced caused by uncompensated spins, while samples LaFe_0.8Cr_0.2O₃ and LaFe_0.7Cr_0.3O₃ show a very small H_c of 75.5 and 28.1 Oe, respectively, because of surface oxide formation and exchange coupling/bias at the resulting interface might be the reason for that drop [27, 54]. Table 3 provides a summary of the magnetic parameters attained from the room-temperature magnetic hysteresis loops for whole compositions. Figure 13 shows that the H_c value gets reduced until LaFe_0.7Cr_0.3O₃, and this behavior may be attributed to cluster spin [15]. The position of the Fe^+ 3 and Cr^+ 3 ions, where the Fe^+ 3 ions are present in a mostly B-site, is where the deviation from the ideal perovskite is most apparent. Because the ordering of Fe moments is somewhat canted rather than precisely antiparallel, there is little net magnetization as a result, which leads to the weak FM that we have previously described [37, 52]. The tilting that decreases a net magnetic moment perpendicular to the uniaxial magneto-crystalline anisotropy is induced by the Dzyaloshinsky-Moriya antisymmetric exchange. The orthoferrite structure exhibits some distortion, as previously noted by C. Gökhan Ünlü et al. [34], which is attributed to the tilts of the octahedral units [FeO₆] around the b and c axes, as seen in Fig. 14. This distortion affects the AFM ordering between Fe³⁺ ions and results in a considerable reduction of the ideal bond angle of 180^o. Weak FM behavior appears to be a result of the alignment of the Fe³⁺ moments being somewhat canted and the LFO structure exhibiting net magnetization [34].

Table 3 Magnetic parameters, anisotropy constant K calculated from M(H) curves of LaFe_1−xCr_xO₃ (x = 0.0, 0.1, 0.2, 0.3, 0.4, and 0.5)

Fig. 13

Variation of Coercivity (Hc) with Cr substitution (x)

Fig. 14

The irregular tilted octahedral [FeO₆] for perovskite LaFe_0.6Cr_0.4O₃, drown using diamond software

The variation in the perovskites’ reciprocal molar magnetic susceptibility (1/χ_M) with absolute temperature in a 1.55 KOe applied field is illustrated in Fig. 15 for LaFe_1−xCr_xO₃, with (x = 0.0, 0.2. 0.4, and 0.5) at a temperature range of (400–900 K). It is obvious that as temperatures rise, the values of 1/χ_M rise as well. It is conceivable for some antiferromagnetic phases to exist as well as for local magnetic phase separation to cause a reduction in susceptibility. The curves 1/χ_M(T) for samples under investigation were examined using the Cuire–Weiss formula [56]. The susceptibility of FM materials given according to Eq. 7:

Fig. 15

Temperature dependence of inverse molar susceptibility (χ_M⁻¹) for perovskites LaFe_1−xCr_xO₃, (x = 0.0, 0.2, 0.4, and 0.5)

$$\chi ~ = \frac{C}{{T - \theta }}~,$$

(7)

where C = N_Aµ_B² µ_eff²/3k_B is the Curie constant, N_A is Avogadro number, µ_B is the Bohr magneton, ${\mu }_{eff}={\mu }_{B} g \sqrt{S(S+1)}$ is the effective magnetic moment, g=2 is the gyromagnetic ratio, and S is the magnetic spin, k_B is Boltzmann constant, and θ is the paramagnetic Weiss temperature. We determined θ from the intercept of the straight line with the temperature axis for the set of χ_M⁻¹(T) curves, where the positive θ values pointing to the FM nature of the prepared samples, as listed in Table 4. One could suggest that a superparamagnetic (SP) behavior is obtained by comparing the hysteresis loops to the behavior of χ_M⁻¹ (T). One may then explain this trend by arguing that if Cr⁺³ ions take the place of Fe⁺³ ions, two factors occur on the magnetic sublattice of octahedral [FeO₆]. The first is that when the Cr substitution is raised, the magnetic lattice is diluted, and the FM arrangement switches from a short-range to a long-range one. With an increase in Cr³⁺ doping, the FM character is weakened, and after that, the effective magnetic moment (µ_eff) has been reduced, as displayed in Table 4. The exchange interaction J_ex/K_B is also reduced by increasing the Cr content, as illustrated in Fig. 16. The second involves lessening the tilting of the octahedra (FeO₆) while increasing the Cr substitution in a bid to enhance their ferromagnetism.

Table 4 Values of calculated Curie temperature (T_C), the Curie constant (C), Curie–Weiss temperature (θ), effective magnetic moment µ_eff, and exchange interaction constant (J_ex/K_B) for LaFe_1−xCr_xO₃ (x = 0.0, 0.2, 0.4, and 0.5)

Fig. 16

Variation of the exchange interaction constant (J_ex/K_B) with the Cr content (x)

On the other hand, the χ_M(T) and M(T) curves of the samples (x = 0.0, 0.2, 0.4, and 0.5) reveal the weak FM character and a significant drop in χ_M because of the non-magnetic nature of Cr³⁺ ions when they replace Fe³⁺ ions in the crystal lattice of LaFe_1−xCr_xO₃ as shown in Fig. 17a. The Curie temperatures (T_c) for LaFeO₃, LaFe_0.8Cr_0.2O₃, LaFe_0.6Cr_0.4O₃, and LaFe_0.5Cr_0.5O₃ were determined based on M(T) graphs, as shown in Fig. 17b. The values of T_c were reduced from approximately 730 K for LaFeO₃ to 682 K for LaFe_0.5Cr_0.5O₃. There are two magnetic sublattices in orthoferrites, one for the iron ions Fe³⁺ and the other for RE (La³⁺). In our present case, the impact of the magnetic properties is controlled by the Fe³⁺ sublattice denoted by the octahedron [FeO₆], since the La³⁺ ion has a diamagnetic nature. By increasing the substitution level of Cr³⁺, the interaction of Cr³⁺–O²⁻–Cr³⁺ is very weak, and the Cr³⁺ (d₃) dilutes the antiferromagnetic (Fe³⁺–O²⁻–Fe³⁺ (d₅)) matrix, leading to reduced magnetization.

Fig. 17

Variation of a molar magnetic susceptibility (χ_M) with absolute temperature (T), b magnetization as a function of temperature for perovskites LaFe_1−xCr_xO₃, (x = 0.0, 0.2, 0.4, and 0.5)

In FM materials, the magnetizations are parallel aligned as a result of exchange coupling between their nearest neighbors. As explained in Heisenberg Hamiltonian notation, the exchange coupling between spins closest to each other could be expressed as follows [29, 57, 58]:

$${\text{E}}_{{{\text{ex}}}} = {\text{ }} - \,{\text{2J}}_{{{\text{ex}}}} {\text{SiSj}} = - \,{\text{2J SiSj cos}}\theta,$$

(8)

where J_ex is the exchange integral, and S_i and S_j are two nearby spins. Whether we have FM or AFM coupling depends on the sign of J_ex, which is + ve for ferromagnetic materials. The electrons travel between nearby atoms when the interatomic distance is small; according to Bethe and Slater [59], this increases the antiparallel ordering, and a -ve value of J_ex will be obtained (AFM material).

Based on the Weiss field theory [27], J_ex for typical perovskites were calculated from Eq. 9, which illustrates the relationship between T_C and J_ex in the FM case.

$${\text{J}}_{{{\text{ex}}}} = \frac{{3{\text{K}}_{{\text{B}}} {\text{T}}_{{\text{C}}} }}{{2{\text{Z}}\;{\text{s}}({\text{s}} + 1)}} ,$$

(9)

where s is the spin (s = 5/2 for Fe³⁺ ion), Z is the number of molecules in the unit cell. The values of J_ex are reported in Table 4.

The total magnetic moment was determined according to the relation [57, 58]:

$${\mu }_{B}=g \sqrt{s (s+1)}.$$

(10)

Since the highest magnetic saturation occurred at x = 0.2; therefore, the µ_cr+3 was determined based on Eq. 10 and found to be 0.046 µ_B. This value is very close to the experimental value obtained from M–H loop as shown in Fig. 12. Thus, one may conclude that the increase of the amount of Cr^+ 3 ions up to x = 0.2, some of the Cr³⁺ ions tend to fill the tetrahedral site instead of the octahedral site of orthorhombic perovskites crystal structure.

4 Conclusion

The perovskite samples LaFe_1−xCr_xO₃ (X = 0.0, 0.1, 0.2, 0.3, 0.4, and 0.5) were synthesized by wet-chemical sol–gel auto-combustion route. All compositions crystalize in orthorhombic structure with Pnma symmetry, without any impurity phases from starting materials, according to a structural investigation using powder XRD analysis. With increasing Cr substitution at Fe site, the cell volume decreases because of the difference in the ionic radii of Fe^+ 3 and Cr^+ 3 ions. Because of the disparity in ionic radii between Cr^+ 3 and Fe^+ 3 ions, the tolerance factor demonstrated the prepared compositions’ phase stability and showed a considerable rise with increasing Cr^+ 3 content at the expense of Fe^+ 3 ions. The mean crystallite size of the produced samples was estimated using the W–H plot based on XRD data, which show variety from 16.12 to 57.29 nm. By using HRTEM micrographs to further investigate the microstructure of all the investigated samples, it was discovered that the particles are quasi-spherical and quite close to the XRD crystallite size. The SAED patterns of the produced orthoferrites revealed spotty ring patterns compatible with the XRD data, indicating the crystallization of samples in orthorhombic structure. The electron density visualization shows an increase in ED around the La³⁺ ions in 4c sites and relatively substantial displacements in the various oxygen positions in the unit cell. The magnetization of the samples depending on composition and is primarily caused by Fe³⁺–O²⁻–Fe³⁺ and Cr³⁺–O²⁻–Cr³⁺ superexchange AFM interactions, according to the M(H) loops of the perovskite system, showed weak FM behavior, due to the canted spin and uncompensated spins at the surface. The change of state of spin of Cr ions and their migration from octahedral site to tetrahedral site leads to the increase of saturation magnetization up to concentration of 20%. These unique features may enable the prepared perovskites to be employed in the fields of memory storage and magneto-optical devices.