Introduction

The rapid development of the global economy requires increased energy resources and thus more efficient energy storage devices [1]. In recent years, emphasis has also been placed on minimizing the impact of fossil fuel usage on the environment [2]. Electrochemical capacitors, known as supercapacitors, are devices that meet the above characteristics [1, 3]. Electrochemical capacitors are characterized by remarkable cyclicity (up to 100 times greater than that of a battery), high power density compared to batteries and a relatively large amount of stored energy. Moreover, their advantage is the ability to quickly charge/discharge [4]. Furthermore, the global market for supercapacitors is dynamically growing, with a market capitalization predicted to reach almost $17 billion by 2027 [5]. Nevertheless, currently achieved energy densities remain the main technological parameter for further improvement of supercapacitors. As the energy density is expressed as half the product of the capacitance and the square of the device voltage (E = ½ CU2), a higher E value can be obtained by varying the values of capacitance (C) and voltage (U). New electrode materials are being developed extensively throughout the world to achieve high capacitance values, and appropriate electrolytes are selected to ensure operation over a wide voltage range [4, 6]. The electrodes that are most commonly used are made of activated carbon [7,8,9,10,11] due to its high conductivity, highly developed inner surface, polarizability, high chemical stability and corrosion resistance, and relatively low cost [12, 13]. In addition, other carbon materials, e.g., graphene, are increasingly being used in this role [3]. However, the inherent hydrophobicity of carbon materials is a common problem that prevents sufficient electrode penetration by the electrolyte [14]. As scientists have recently paid attention not only to the specific surface area of supercapacitor active materials but also to their hydrophilicity, attempts have been made to reduce the hydrophobicity of the materials [14, 15]. Nevertheless, hydrophilic additives are mostly insulating materials, leading to deterioration of the bond between the graphene sheets and thus the conductivity of the material. It is possible to enhance the hydrophilicity of graphene-based materials by C–C hexagonal lattice doping with heteroatoms, which also shows a beneficial effect of increased capacitance due to the improvement of ion mobility at the electrode/electrolyte interface [14].

Electrolytes play an important role in the determination of supercapacitor electrochemical properties. Several types of electrolytes can be used in supercapacitors, based on porous carbon materials: solutions of organic salts in aprotic solvents [4, 16, 17], aqueous solutions of acids, bases and salts [4, 8, 18, 19], and ionic liquids [4, 8, 16, 20]. Most of the supercapacitors available on the market use organic electrolytes, which enable the supercapacitors to operate within a wide potential window (2.7–3.0 V). Unfortunately, such electrolytes pose a risk to the environment, are quite expensive and require a complicated assembly process compared to aqueous electrolytes [8]. Although the highest operating voltages are obtained when using ionic liquids (up to 3.5 V), these electrolytes are characterized by low ionic conductivity and high viscosity, limiting the achievement of high specific power values [20, 21]. The specific energy density values for commercial electrochemical capacitors with organic electrolytes are in range of 8–10 Wh kg−1. The theoretical stability window for the most commonly used solutions of acids (H2SO4) or bases (KOH) of aqueous electrolytes is limited due to the theoretical potential for water decomposition (1.23 V) [22]. Consequently, the operating voltage of activated carbon supercapacitors using these electrolytes is low (approximately 1.0 V). It has been shown that electrochemical capacitors using electrodes with highly porous carbon materials operating in a neutral environment can achieve a wider electrochemical window due to the high cathodic overpotential of the hydrogen evolution reaction noticed at neutral pH [23]. Neutral aqueous electrolytes are also characterized by features that make them an attractive working environment for supercapacitors: environmentally friendly, inexpensive and noncorrosive [23,24,25].

More than 10 years ago, the first attempts were made to enhance the energy density in two-electrode symmetrical systems operating in an aqueous environment [26,27,28]. Demarconnay et al. [26] constructed a symmetrical device based on commercial activated carbon, which worked in 0.5 M Na2SO4. This supercapacitor showed operation in the voltage range up to 1.6 V, achieving a capacity of 135 F g−1. Notably, the device could work up to a voltage of 2.0 V using the same set of electrode materials and electrolyte for the three-electrode system. Shivakumara et al. [27] used 1 M Na2SO4 as a neutral electrolyte and a carbon-based electrode material (partially exfoliated-reduced graphite oxide) to build symmetrical supercapacitors. Their properties were studied in two-electrode and three-electrode systems. For the case of the two-electrode setup, a stable performance of up to only 1.6 V was achieved due to oxidation of the electrode material, which prevents efficient operation at higher voltages. The supercapacitor attained a capacity of 92 F g−1 and an energy density of 8.2 Wh kg−1. For the three-electrode system, it was possible to extend the operating window, as in the Demarconnay et al. [26] article, to 2.0 V. Bello et al. [28] investigated the properties of AC foam based on graphene and polyvinyl alcohol. Electrochemical tests in a symmetric two-electrode system were performed using 1 M Na2SO4 and the potential window achieved was 1.6 V. The assembled device exhibited a capacitance of 65 F g−1, an energy density of 12 Wh kg−1 and a power density of 0.4 kW kg−1. The examples mentioned above show that the narrow potential window is a drawback of supercapacitors filled with aqueous electrolytes. To obtain higher values of current and power density, it is necessary to ensure that the devices can operate at higher voltage.

In this work, we investigated the influence of the specific surface area of the electrode material and surface chemistry-related hydrophilicity on the electrochemical parameters of a symmetric supercapacitor. The devices working in a neutral electrolyte (2 M NaClO4) were built, which, according to the literature, enables operation over a wide potential window. The electrochemical behavior of a commercially available activated carbon with a material with reduced hydrophobicity, phosphorus-doped graphene was compared. Although a supersaturated NaClO4 electrolyte is currently heavily investigated for supercapacitor applications, we investigated capacitor performance with a dilute electrolyte (< 3 M), as water-in-salt highly concentrated NaClO4 electrolytes exhibit lower viscosity and diffusion coefficients [29]. After analyzing the results and noticing the unfavorable phenomenon of cell failure caused by the use of the diluted electrolyte, we decided to extend our research. The 2 M NaClO4 was replaced by 1 M Na2SO4, a neutral, same cation-type aqueous electrolyte with high solubility in water, limited oxygen solubility and good electrical conductivity.

Experimental methods

Preparation of graphene material

Graphene oxide (GO) used as a starting material for the preparation of the P-doped graphene material was prepared using a modified Hummers [30] method, as described previously [31]. P-rGO was obtained by adding 2.025 mL of phytic acid (50 wt%, Sigma-Aldrich) to 100 mL of previously obtained GO (1.45 mg ml−1). Then, the mixture was ultrasonicated for 1 h to obtain a homogeneous dispersion and placed into a hydrothermal stainless steel autoclave (Parr Instrument Company). The reaction was carried out at 180 °C for 6 h under constant stirring at 200 rpm. The as-received product was washed with Milli-Q water and finally vacuum-dried overnight at 60 °C.

Physiochemical characterization

X-ray diffraction (XRD) analysis was performed to determine the crystallographic structure of the materials. The measurements were taken using an Ultima IV Rigaku diffractometer with Cu Kα radiation. Scanning electron microscopy (SEM) images were recorded using a Helios NanoLab 450-FEI to examine the morphology of the graphene material. The porosity of the materials was examined by N2 sorption at 77 K using an Autosorb IQ gas sorption analyser (Quantachrome). The specific surface area (SBET) was calculated according to the Brunauer–Emmet–Teller (BET) method based on nitrogen isotherm data obtained in the relative pressure (p/p0) range of 10−5–0.98. The pore size distributions (PSD) were studied by quenched solid density functional theory (QSDFT). The surface chemistry of P-rGO and AC was determined by X-ray photoelectron spectroscopy (XPS) using a PHI 5000 VersaProbe instrument. The C1s, O1s and P2p core-level spectra were deconvoluted using CasaXPS software into separated peaks. The contact angles of Milli-Q water for the investigated electrodes were conducted by a sessile drop method [32] using the OCA 15 EC contact angle meter (DataPhysics Instruments GmbH, Germany). The images were captured and analyzed using the SCA software (DataPhysics Instruments GmbH, Germany).

Electrochemical measurements

Electrochemical measurements were taken in a three-electrode cell and a full symmetric system in two selected aqueous electrolytes (2 M NaClO4 and 1 M Na2SO4). Carbon-based electrodes were used as working (WE) and counter electrodes (CE) with balanced masses (mWE = mCE) in a symmetric configuration and were separated by glassy fibrous paper (Whatman®). In a three-electrode configuration, we used a silver chloride reference electrode and CE was made of activated carbon labeled as MPK, which was obtained by KOH activation of pitch semi-coke followed by hydrogen annealing at 800 °C. Electrodes were made in a form of tablets, from powders (P-rGO and Norit DLC Super 50) with polyvinylidene fluoride (PVDF, Kynar Flex) binder and carbon black with a respective mass ratio of 85:10:5 in the presence of 1 mL of acetone. Electrodes were pressed in a mold with a pressure of 8 tons for 1 min. The total weight of the electrodes in the assembled cells ranged from 14 to 17 mg. In order to measure the negative and positive electrode electrochemical behavior during symmetric cell operation, the Ag|AgCl reference electrode was introduced and the appropriate measuring protocol was selected in the Biologic EC-Lab software, allowing to measure the whole cell voltage and respective WE and CE potentials, separately.

The electrochemical measurements were taken using a Biologic VSP potentiostat–galvanostat. Cyclic voltammetry (CV) measurements with varying scan rates from 1 to 100 mV s−1 and GCD experiments at current densities ranging from 0.2 to 20 A g−1 were taken in the potential range from 0 to 2.0 V. Moreover, electrochemical impedance spectroscopy (EIS) in the frequency range of 400 kHz–10 mHz at an AC amplitude of 5 mV and DC potential of 0 V (vs. Eoc) was used for the assembled device along with cycling stability measurements at a current density of 1 A g−1.

The specific capacitance per electrode (Csp F g−1) can be calculated by using Eqs. (1 and 2):

$$C_{{{\text{sp}},{\text{GCD}}}} = \frac{I\Delta t}{{m\Delta V}}$$
(1)

where I is the discharge current (A), Δt is the discharge time (s), m is the mass of the active material of a single electrode (g) and ΔV is the applied voltage once the total resistance drop is subtracted (V).

$$C_{{{\text{sp}},{\text{CV}}}} = \frac{{\smallint I{\text{d}}V}}{vm\Delta V}$$
(2)

where \(\int I\mathrm{d}V\) is the integrated area under the CV discharge curve, v is the scan rate (mV s−1), m is the mass of the active material of a single electrode (g) and ΔV is the applied voltage (V).

The stored specific energy (E in Wh kg−1) and the specific power delivered (P in kW kg−1) by a symmetric supercapacitor were calculated using the following equations:

$$E = \frac{{C_{{{\text{sp}},{\text{GCD}}}} V^{2} }}{8 \times 3.6}$$
(3)
$$P = \frac{3.6E}{{\Delta t}}$$
(4)

where Csp is the specific capacitance (F g−1), V is the cell voltage (V) and Δt is discharge time (s).

The imaginary C″ (ω) part of the capacitance as a function of frequency (F g−1) was calculated as follows:

$$C^{\prime \prime } (\omega ) \, = \frac{{Z^{\prime } \left( \omega \right) }}{{M\omega \left| {Z\left( \omega \right)} \right|^{2} }}$$
(5)

where Z’ (ω) is the real part of the impedance (Ω), Z(ω) is the total impedance (Ω) and M is the mass of both electrodes (g).

The relaxation time constant τ0 (s) was calculated according to the equation:

$$\tau_{0} = \frac{1}{{f_{0} }}$$
(6)

where f0 is the frequency at which the imaginary capacitance reaches a maximum value (Hz).

Results and discussion

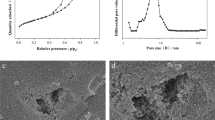
In our work, we investigated the electrochemical performance of two carbon materials that are at the opposite end of the spectrum in terms of both porous characteristics and surface chemistry. We compared highly porous activated carbon with a low amount of oxygen functionalities versus phosphorus-doped rGO with limited porosity. The textural properties of AC and P-rGO were examined by N2 sorption at 77 K (Fig. 1) with the data derived from the measurements presented in Table 1. Additionally, to emphasize the changes in the textural parameters of the modified graphene-based material, undoped rGO was included in the investigations. According to the IUPAC classification [33], rGO and P-rGO are characterized by a type IV isotherm with a hysteresis loop, and AC exhibits a type I isotherm (Fig. 1a). The graphene materials show various microporous and mesoporous attributes with the pore size distribution profiles showing maxima at values of approximately 0.72, 1.68 and 3.10 nm and 0.92, 1.68 and 3.39 nm for rGO and P-rGO, respectively (Fig. 1b). The pore size distribution confirms that Norit DLC Super 50 has a microporous structure with a predominant contribution of pores with a width lower than 2 nm. The BET surface areas (SBET) of AC, rGO and P-rGO are 1601, 453 and 233 m2 g−1, respectively (Table 1). Compared to P-rGO, SBET is over six times higher and the contribution of micropores is twofold higher in the AC structure. The relatively low porosity of P-rGO is a result of functionalization of rGO, which implies micropore blocking with P-functional groups and restacking of the graphene sheets [34].

Figure 1
figure 1

N2 adsorption/desorption isotherm at 77 K (a); pore size distribution of materials (b)

Full size image
Table 1 Textural parameters for the graphene materials and Norit DLC Super 50 obtained from the analysis of N2 sorption at 77 K
Full size table

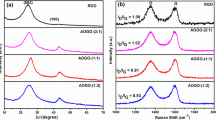
The crystalline structure of AC and P-rGO was determined using XRD, and the results are given in Fig. 2. The diffraction patterns for P-rGO show sharp peaks at 24.8 and 43.2°, which can be assigned to the (002) and (100) planes and confirm the reduction of graphene oxide [34, 35]. These spectra are consistent with the data reported in the literature [36, 37]. The XRD pattern for AC presents two broad peaks at approximately 2θ = 23.8 and 43.5° corresponding to the (002) and (100) planes, respectively. The two broad peaks suggest a low crystallinity for Norit DLC Super 50. The interlayer distance (d002) for rGO, P-rGO and AC is 0.360, 0.365 and 0.374 nm, respectively, while the calculated crystallite size (Lc) is 3.4, 1.5 and 1.7 nm.

Figure 2
figure 2

XRD patterns for rGO, P-rGO and AC

Full size image

P-rGO consists of tightly packed and deformed sheets (Fig. 3a–c), which are characteristic of graphene materials obtained from hydrothermal synthesis [38]. The material shows a typical three-dimensional porous and aggregated network structure. At high magnification (Fig. 3a), accumulation of very small nanoparticles, formed during hydrothermal treatment, is observed on the graphene nanosheets. Since at a temperature of approximately 160 °C, the decomposition of phytic acid is followed by the removal of hydroxyl groups [39], the existence of nanoparticle aggregates with phosphorus-containing functional groups is observed (marked with a circle). Further EDS mapping analysis shows a uniform distribution of phosphorus within the graphene material (Fig. 3f). This implies that the hydrothermal reduction not only results in the formation of a P-doped graphene material but also leads to its uniform doping into the graphene material structure. Furthermore, the even distribution of oxygen atoms on the surface is also noticeable, which influences the formation of phosphate linkages with the defective sites on the graphene surface (Fig. 3e).

Figure 3
figure 3

SEM images at different magnifications (a–c) and EDS elemental mapping analysis of P-rGO (d–f)

Full size image

To analyze the surface chemistry of P-rGO and AC, the XPS measurements were taken. The C, O and P contents in the studied materials are shown in Table 2. P-rGO was characterized by a lower carbon content than AC (83.3 vs. 96.1 at%, respectively) but it contains many more oxygen species on the surface (15.3 vs. 3.9 at%). As given in Table 2, P-rGO contains 1.4 at% phosphorus, therefore taking into account the amount of heteroatoms, the surface of P-rGO can be considered more hydrophilic than that of AC (16.7 vs. 3.9 at%). Carbon speciation in P-rGO was investigated by deconvolution of the high-resolution C1s core-level spectra (Fig. 4a). The content of each type of carbon was calculated by multiplying the total carbon content by the contribution of each deconvoluted peak to the overall C1s spectrum (Table 2). The XPS C1s spectrum obtained for P-rGO was deconvoluted into seven peaks. The main peak at a binding energy of 284.5 eV is attributed to carbon with sp2 hybridization (46.9 at%) [40]. The higher contribution of carbon in sp2 hybridization in P-rGO compared to the sample of GO noted in the literature (22%) [31] confirms the reconstruction of the graphene structure during the simultaneous hydrothermal reduction and phosphorus doping. Moreover, a visible peak at a bonding energy of 285.4 eV represents the carbon with sp3 hybridization [25], which amounts to 4.5 at% of the P-rGO. The remaining peaks in the C1s spectrum at binding energies of 286.0 eV, 287.8 eV and 288.6 eV are attributed to the epoxy, carbonyl and carboxyl groups, respectively, while the two satellite peaks for C–C are visible at 290.4 and 291.8 eV [21, 22]. The O1s spectrum shows the presence of oxygen, which is the result of the incomplete reduction of graphene oxide [39]. The O1s peak illustrates the presence of two components at binding energies of 530.9 and 532.7 eV, which suggest the presence of C=O/P=O/O–H and C–O/C–O–P/P–O–P groups at the surface of the material, respectively [31, 40, 41]. The signal observed at 133.6 eV in the P2p core-level spectrum (Fig. 4c) corresponds to pyrophosphate [P2O7]4− bonding. Furthermore, the peak at a binding energy of 134.5 eV can be ascribed to metaphosphate [PO3]− functional groups [22, 42]. It can be observed that phosphorus is not incorporated through a direct C–P bond into the graphene structure. This element is bound to the graphene nanosheets by oxygen bridges (C–O–P, phosphates). At the AC surface, the most dominant peak is related to the C–C bonds in sp2 hybridization (64.3 at%) with a lower contribution of C–O groups, which aligns with the high-temperature synthesis conditions and hydrophobic nature of such materials. A higher content of carbon in sp2 hybridization (64.3 vs. 46.9 at%) provides the material with good conductivity and thus leads to an improvement in the rate capability and power density.

Table 2 P-rGO and AC chemical composition determined by XPS (at%)
Full size table
Figure 4
figure 4

C1s (a), O1s (b) and P2p (c) high-resolution spectra for P-rGO

Full size image

To test the electrodes wettability [43, 44], the deionized water droplets of 0.2 μL were formed at the end of the syringe and deposited at random locations on each material surface. The reported contact angle values were averaged on ten measurements. The contact angle value (Fig. 5) on the surface of P-rGO (94.9°) is lower than that of AC (110.8°), suggesting that the hydrophilic phosphate and oxygen functional groups on the surface of P-rGO improve the overall hydrophilicity of the electrode active material [45]. The introduction of P-functional groups in graphene enhances wettability, thus ensuring a more efficient transport of the electrolyte ions at the electrode surface [46].

Figure 5
figure 5

Water contact angle of P-rGO and AC electrodes

Full size image

The electrochemical performance of the materials was evaluated in a two-electrode cell configuration, using two different neutral aqueous electrolytes. First, CV measurements were taken in the potential range of 0.8–2.0 V to determine the widest safe operating voltage for a symmetrical capacitor. The safe working potential is the potential at which the anodic current does not exceed 120% of the current that shows a linear nature and undisturbed capacitive performance. The CV curves measured at a voltage of 2.0 V and a scan rate of 1, 10 and 50 mV s−1 are shown in Fig. 6.

Figure 6
figure 6

CV curves of the symmetric devices based on P-rGO and AC in neutral electrolytes recorded at a scan rate of 1 mV s−1 (a); 10 mV s−1 (b); and 50 mV s−1 (c)

Full size image

At low scan rate, the electrolyte ions are effectively diffusing into the carbon material structure, and therefore, the electrodes achieved a higher value of specific capacitance [47] (Fig. 6a). However, at a high scan rate, charging and discharging was too fast for the completed ion diffusion, and as a consequence, less utilization of the electrode surface resulted in a lower specific capacitance [39, 47]. Furthermore, with increasing scan rate to 50 mV s−1, CV curves became rectangular in shape, suggesting a reversible capacitive mechanism of energy storage (Fig. 6c).

The CVs recorded at 10 mV s−1 (Fig. 6b) for both AC-based electrodes display a nearly rectangular shape; nevertheless, the material containing phosphorus shows a noticeable resistance. This shape for the CV curves is attributed to the electrical double-layer (EDL) feature of the materials in the perchlorate electrolyte. The deformation of the voltammetric characteristics for the phosphorus-containing graphene material is noticeable with a small, wide hump distributed from approximately 0.5 to 1.3 V due to the additional pseudocapacitive effect, which originates from the high content of superficial oxygen functional groups [48]. When the properties of AC are compared in two different electrolytes, it can be observed that at the same scanning rate (10 mV s−1), the voltammograms differ to an extent. The shape of the CV curve for 2 M NaClO4 indicates better charge propagation, while the deviation from the ideal shape for the supercapacitor, tested in 1 M Na2SO4, indicates slower diffusion of ions into or out of the micropores. Both electrolytes and materials enable a supercapacitor to operate above the theoretical potential of water decomposition (1.23 V). This enables higher operating voltages to be achieved, which implies higher values for the stored energy.

The literature contains numerous studies of supercapacitors consisting of various electrode materials and an aqueous electrolyte at different concentrations. Shivakumara [27] and Zhao [48] were able to construct devices that work stably within the maximum potential range of 1.6–1.8 V. Symmetrical supercapacitors were tested in 1 M Na2SO4 in a two-electrode cell, with one composite containing carbon nanofibers and the other a partially exfoliated and reduced graphite oxide as an electrode material. The ability to operate at a voltage of 2.0 V and above can be realized for an EDLC containing sodium perchlorate as the electrolyte. Dou et al.’s [49] symmetrical two-electrode system with AC as electrodes and 17 m NaClO4 was able to operate in the maximum voltage window of 2.2 V. However, the wide voltage range did not significantly affect the capacitance values (less than 35 F g−1 in the current range 0.1–20 A g−1). Bu et al. [50] constructed a device based on commercially available AC and used the same electrolyte (17 m NaClO4). The supercapacitor, also for the two-electrode system, achieved similar specific capacitance values (29–33 F g−1), and moreover, the device was able to work stably in a slightly higher voltage range (2.3 V). Stable performance in a higher-voltage window is related to a highly saturated electrolyte and transitions into a water-in-salt system where the mobility of ions is significantly different than that of traditional diluted aqueous electrolytes due to the increased viscosity and decreased diffusion coefficients of ions and water molecules [29].

To investigate positive and negative electrode potentials, the experiments for all devices were performed in a modified three-electrode cell equipped with a silver–silver chloride reference electrode; however, investigations were conducted with adapted measurement conditions to register symmetric cell performance. This method allows recording of electrode potentials separately during the operation of the supercapacitor between 0 and 2.0 V [51]. The GCD profiles of symmetric supercapacitors based on P-rGO and AC at a current density of 1 A g−1 are presented in Fig. 7a–c and in Fig S1 at the current densities of 0.5 and 5 A g−1. The AC-based devices are characterized by a practically symmetric triangular shape for the curves, which prove a capacitive behavior [52]. For the case of cells operating in 2 M NaClO4 electrolyte, it is clear that the positive electrode exhibits a greater contribution within the symmetric setup. The operating potential window for AC and P-rGO operating in 2 M NaClO4 for the anode and cathode are equal to [− 0.27; 0.85], [− 0.40; 0.95] and [− 1.15; − 0.27], [− 1.05; − 0.40] V versus Ag/AgCl, respectively. At the same current regime, P-rGO exhibits a capacitive performance that is different from that of electrodes composed of AC, which is convergent with the results obtained from the CV experiments. The shape of the GCD curve for P-rGO shows some degree of distortion, and this deformation can be caused by the pseudocapacitive effect of the active material during charging and discharging [52, 53].

Figure 7
figure 7

GCD profiles of the symmetric supercapacitors at a current density of 1 A g−1 for AC 2 M NaClO4 (a); P-rGO 2 M NaClO4 (b); AC 1 M Na2SO4 (c); specific capacitance versus discharge current densities (d). Full black line represents the GCD profile of the full cell, and dashed violet and green lines represent the profiles of the positive and negative electrodes of the cell, respectively

Full size image

The GCD profile for the AC-based capacitor working in 1 M Na2SO4 shows that the contributions of the operating potential window of the positive and negative electrodes are almost equal (Fig. 7c). If the supercapacitor is charged between 0 and 2.0 V, the operating potential windows for the positive and negative electrodes are [− 0.09; 0.84] and [− 1.16; − 0.09] V versus Ag/AgCl, respectively. The longer charging and discharging time observed for the AC-based supercapacitors compared to those for the P-rGO-based device corresponds to a higher available capacity [53], calculated using Eq. (2), which is presented in Fig. 7d. It is observed that for P-rGO, the negative electrode works at a potential of 1.35 V (Fig. 7b), which is above the theoretical potential of water decomposition. Noticeably, in devices using 2 M NaClO4, the maximum voltage of the supercapacitor is limited by the anode [23, 26]. If an excessively high-voltage is applied to the positive electrode, irreversible oxidation of the carbon material occurs, and the evolution of hydrogen takes place on the negative electrode [27]. The above GCD results explain the worse behavior of 2 M NaClO4-based supercapacitors during long-term performance.

The dependence of the specific capacitance as a function of current density is shown in Fig. 7d. In the low current density range (0.2–1 A g−1) for AC, the factor determining the capacitance value is the size of the hydrated ion. However, at larger current regimes (1–20 A g−1), the achievement of higher capacitance values is the result of a better ionic conductivity and electrolyte ions mobility. This phenomenon and the decrease in specific capacitance with an increase in current density are attributed to the limited diffusion of electrolyte ions into the electrode micropores with increasing charge current [48, 54]. The electrochemical measurements at low current densities revealed that slightly porous P-rGO meets the capacitive performance of a commercial AC, which implies the significance of the electrode affinity to the aqueous electrolyte. Lower contact angle of the P-rGO than AC (Fig. 5) arising from the oxygen and phosphorus functionalized surface of the material results in greater wettability, followed by improved ion transport at the electrode/electrolyte interface [14]. At current densities above 1 A g−1, the specific capacitance values for AC are similar, and it can be observed that for the graphene material, these values decrease drastically. The result is attributed to the insufficiently developed microporous structure of P-rGO and its smaller specific surface, resulting in obstructed diffusion of electrolyte ions [55].

Based on potential windows for positive and negative electrodes determined from the data retrieved from the assembled aqueous supercapacitors, the CV measurements in a three-electrode setup were taken (Fig. 8 and Fig. S2,S3). The curves of AC 1 M Na2SO4 and P-rGO 2 M NaClO4 show a semi-rectangular shape which can be explained by the presence of electric double-layer capacitance and pseudocapacitive behavior. In the case of AC 2 M NaClO4, two regions of voltammograms can be distinguished. One part of the curve has a rectangular shape (− 1.0 to 0.75 V), suggesting accumulation of charge in the double layer. Well-defined redox peaks (− 1.15 and 0.85 V) can be observed on the edges of the curves. When these voltages are reached, the decomposition of the electrolyte occurs [56].

Figure 8
figure 8

CV curves of AC 1 M Na2SO4 (a); AC 2 M NaClO4 (b); P-rGO 2 M NaClO4 (c) in the three-electrode setup recorded at a scan rate of 10 mV s−1. The green and violet lines represent the material behavior in the potential range of the negative and positive electrode, respectively, for its symmetric counterpart

Full size image

Furthermore, the GCD measurements in the three-electrode configuration (Fig. S4-S6) show that the best electrochemical balance of the material in the potential range of each negative and positive electrode is observed for the AC operating in Na2SO4 electrolyte. What is interesting is that measurements in a three-electrode configuration at higher current densities show more disproportioned capacitive behavior compared with the analogous material measured in a symmetric full device. The specific capacitance value of electrodes constituted of AC 1 M Na2SO4, AC 2 M NaClO4 and P-rGO 2 M NaClO4, according to Eq. (2), at current density 1 A g−1, reach values of 79 and 87 F g−1; 137 and 86 F g−1; and 107 and 13 F g−1, for the positive and negative potential range, respectively (Fig. S5).

There have been many studies comparing the effect of neutral electrolytes on the capacitive characteristics of supercapacitors. Research has focused on aqueous solutions of salts such as Li2SO4, K2SO4 and Na2SO4 [57, 58] and has recently investigated NaClO4 [29, 49, 50]. Scientists study asymmetric supercapacitors more often because of their advantages. One such advantage is that it is easier to widen the potential window, which leads to higher current density values [18]. One property of asymmetric supercapacitors is that they exhibit polarizability. Since the positive and negative electrodes of symmetrical supercapacitors are composed of the same material, theoretically, the supercapacitors do not have true polarizability, limiting the damage caused by reverse polarizability operation [59]. It is worth emphasizing that the supercapacitors assembled in our work were tested in a symmetrical system, and the devices were found to operate efficiently at a voltage of 2.0 V.

The properties of the electrolyte, such as ion conductivity and the size of the hydrated ion, also influence the obtained high capacitance values [50, 59]. Table 3 shows the data gathered from the literature for both electrolytes. It can be observed that the ClO4− ion has a smaller radius for the hydrated ion compared to SO42−, which enhances the adsorption of ClO4− ions at the electrode/electrolyte interface. Furthermore, a high concentration of NaClO4 inhibits water decomposition, which improves device performance, possibly due to a change in the ion solvation structure and reduced water activity [4, 58]. According to the literature, the higher the ionic conductivity, which influences the transport of ions, the higher the capacitance, which is consistent with our experimental data [59].

Table 3 Size of the electrolytic bare and hydrated ions and their conductivity [4, 19, 50]
Full size table

The results of the EIS measurements of the assembled supercapacitors are presented in Fig. 9a. The Nyquist plots show semicircles at high frequencies, suggesting evident charge transfer resistance for all devices [60]. The slope of the straight line in the low-frequency region corresponds to the diffusion resistance in the electrode materials. The more inclined this slope is toward the imaginary axis, the better the capacitive properties [55, 57]. The combined electrolyte resistance and current collector resistance defined as bulk resistance (Rb), determined from the intersection of the Z′ axis for AC in 2 M NaClO4, P-rGO in 2 M NaClO4 and AC in 1 M Na2SO4 is equal to 0.72, 0.76 and 2.29 Ω, respectively [61]. The data obtained are consistent with Table 3 and confirm that the larger the size of the hydrated ion, the higher the electrolyte resistance [62]. The charge transfer resistance Rct (related to the ion transfer at the electrode/electrolyte interfaces and electron transfer between the current collector and the electrode) is equal to 2.44, 1.11 and 2.55 Ω, respectively. Noticeably, the symmetric system with a graphene-based material exhibits resistivity lower than that of the AC-based supercapacitors, where the flake-like structure of P-rGO and the less developed porous structure facilitate charge transport behavior. Furthermore, similarly to the bulk resistance, the Rct of the AC supercapacitor in 1 M Na2SO4 electrolyte is higher compared to the adequate system operating in 2 M NaClO4. This phenomenon is related to the smaller size of the solvated ClO4− anion, as well as the higher molar concentration of 2 M NaClO4, which results in thinner diffuse layers near the electrode surface, higher concentration gradients and therefore improved ionic charge transport [63]. The middle region of the frequency provides information on diffusion behavior in the porous structure of the materials. The smallest Warburg resistance (shortest 45° incline) characterizes AC 2 M NaClO4, indicating undisturbed ion diffusion paths due to a well-developed porous structure [39, 62]. Conversely, less microporous P-rGO-based supercapacitor displays limited electrolyte ion penetration through the pores, which is illustrated by the highest value of Warburg resistance. On the basis of the low-frequency data in the Nyquist plot, it was also determined that supercapacitors based on AC-based electrodes have characteristics that are more similar to ideal EDLC compared to P-rGO.

Figure 9
figure 9

Electrochemical performance of symmetric supercapacitors based on AC and P-rGO electrodes and an aqueous electrolyte; the Nyquist plot with an inset representing the high-frequency range (a); the imaginary part of the capacitance as a function of the frequency (b); Ragone plot of the specific energy–power density dependence of the supercapacitors (c); and the cycling stability at a current density of 1 A g−1 (d)

Full size image

The relaxation time (τ0) calculated from Eq. (6), is the minimum time necessary to discharge all energy from a device, while the efficiency is greater than 50% of its maximum value [64, 65]. These data can be obtained from the frequency at maximum C″, received from Eq. (5), and are shown in Fig. 9b. The obtained relaxation time constants reveal the differences in electrochemical characteristics between the supercapacitors. The τ0 values of 7.94 s, 12.65 s and 15.85 s were achieved for AC in 2 M NaClO4, P-rGO in 2 M NaClO4 and AC in 1 M Na2SO4, respectively. These results show that the supercapacitors can fully deliver their stored energy in a different time. Based on the obtained results, both the active material of the electrode and the electrolyte influence the divergent τ0 values [65, 66]. When comparing the relaxation time determined for the device using 2 M NaClO4, the AC shows lower values compared to P-rGO (7.94 vs. 12.65 s). The larger specific surface area of AC ensures a faster exchange of electrolyte ions and thus a shorter response time for the supercapacitor. The use of AC as an active material and 1 M Na2SO4 as an electrolyte results in an almost doubling of the value of τ0 value compared to 2 M NaClO4 (15.85 vs. 7.94 s). The reason for this is due to the larger size of the hydrated sulfate anion and lower molar concentration of the Na2SO4 electrolyte.

The dependence of specific energy on the power density, which were calculated according to Eq. (3) and (4), respectively, is presented in Fig. 9c in the form of a Ragone plot. Symmetric supercapacitors can reach a maximum energy density in the range from 11.7 to  Wh kg−1 at a power density of 0.03 kW kg−1, which is a good result compared to carbon-based capacitors described previously [23, 26]. Moreover, energy densities of 5.2 and 1.8 Wh kg−1 at high power densities of 3.6 and 1.3 kW kg−1 for AC in 2 M NaClO4 and P-rGO in 2 M NaClO4, were registered, respectively. Comparing the characteristics of AC in 1 M Na2SO4, it can be observed that the device based on sulfate salt shows slightly worse electrochemical properties. It maintains an energy density of 5.0 Wh kg−1 at a power density of 3.2 kW kg−1.

The long-term performance of the symmetric capacitors was measured at a current density of 1 A g−1. For the first 1000 cycles, AC in 2 M NaClO4, P-rGO in 2 M NaClO4 and AC in 1 M Na2SO4 retains 97.2, 95.6 and 98.9% of the initial capacity, respectively. The use of 2 M NaClO4 results in significantly worse stability: P-rGO in 2 M NaClO4 after 2000 cycles retains 87% of its initial capacity, and AC in 2 M NaClO4 stops working after 1100 cycles of operation. A sudden drop in capacity was observed, and for the first 1000 cycles, the device retained more than 95% of the original capacity value (Fig. 9d). It is possible that during the long-term use of devices, excessive voltage leads to the decomposition of water near the anode or cathode, resulting in deterioration of cycling stability [37]. Another explanation that can be taken into account is increased oxygen solubility in the diluted NaClO4 electrolyte, resulting in increased susceptibility for electrode oxidation and cell corrosion [67]. Phosphorus-containing materials are known in the literature [68] as oxidation retardant compounds, which results in longer operation of the device based on P-rGO. For comparison, after 2000 charge–discharge cycles, the AC working in the 1 M Na2SO4 solution still retains almost 99% of its original capacity.

Conclusions

We have investigated the electrochemical performance of two different carbon-based supercapacitors with a safe operating voltage of 2.0 V in aqueous electrolytes. To achieve efficient operation for the supercapacitor, both the material properties (resistivity, surface chemistry and porous structure) and the type of electrolyte (especially the size of the ions or the conductivity of the solution) are crucial factors. The outcomes of electrochemical studies confirmed that both Na-ion-containing electrolytes (2 M NaClO4 and 1 M Na2SO4) enable operation of the devices above the theoretical potential for water decomposition. Furthermore, in the symmetric setup, both the electrode material and electrolyte type influenced the electrochemical balance between the positive and negative electrodes. However, 1 M Na2SO4 enabled one to achieve better parameters for the electrochemical tests. For the case of the electrochemical performance in 2 M NaClO4, P-rGO, which despite having a more than six times lower specific surface area than AC, allowed for longer and more stable operation of the system due to the greater hydrophilicity of the material surface. A symmetric device based on AC electrodes in 1 M Na2SO4 demonstrated outstanding charge storage properties, including the highest specific capacitance of 94 F g−1 at 0.2 A g−1 and energy density of 13 Wh kg−1. When improving the electrochemical performance of the supercapacitor, not only should the specific surface area be taken into consideration, but also the presence of oxygen functional groups due to their important role in enhancing wettability at the electrode/electrolyte interface should be considered. Our research confirmed that symmetric setups in neutral aqueous electrolytes can be applied as highly effective energy storage devices.