Laser-based additively manufactured polymers: a review on processes and mechanical models

Abstract

Additive manufacturing (AM) is a broad definition of various techniques to produce layer-by-layer objects made of different materials. In this paper, a comprehensive review of laser-based technologies for polymers, including powder bed fusion processes [e.g. selective laser sintering (SLS)] and vat photopolymerisation [e.g. stereolithography (SLA)], is presented, where both the techniques employ a laser source to either melt or cure a raw polymeric material. The aim of the review is twofold: (1) to present the principal theoretical models adopted in the literature to simulate the complex physical phenomena involved in the transformation of the raw material into AM objects and (2) to discuss the influence of process parameters on the physical final properties of the printed objects and in turn on their mechanical performance. The models being presented simulate: the thermal problem along with the thermally activated bonding through sintering of the polymeric powder in SLS; the binding induced by the curing mechanisms of light-induced polymerisation of the liquid material in SLA. Key physical variables in AM objects, such as porosity and degree of cure in SLS and SLA respectively, are discussed in relation to the manufacturing process parameters, as well as to the mechanical resistance and deformability of the objects themselves.

Graphic abstract

Introduction

Initiated in the 1980s, additive manufacturing (AM) has revolutionised the modern industry by introducing a new concept to produce complex geometries from three-dimensional model data [1]. Differently from traditional methods based on material subtraction, AM produces parts by means of successive layers of material that are added on top of each other. Starting from a computer-aided design (CAD), parts are obtained without the need of moulds, cutting tools or other auxiliary resources, and as such, the AM technology can handle parts with very complex geometries with great efficiency and near-zero material waste [2].

In its early age, additive manufacturing was mainly employed for prototyping, with scientists and designers taking advantage of its efficient and cost-effective technology in building models to be used for theoretical studies or product development. Nowadays, the potential of additive manufacturing is exploited in several fields [3], including the aerospace [4], automotive [5], construction [6] and healthcare sectors [7, 8]. New frontiers are being explored in the field of advanced materials science [9, 10], with applications to the design of structured materials [11,12,13,14], stimuli-responsive materials [15,16,17] and bio-printing [18, 19]. The fast diffusion of additive manufacturing points to its advantages, including high precision, flexibility and a vast range of printable materials, comprising metals, ceramics, polymers, hydrogels and composites [20,21,22,23,24,25,26].

Polymeric materials account for the largest share in AM, including thermoplastics, thermosets, elastomers, functional polymers, polymer blends and biological systems. According to the classification of additive manufacturing technologies proposed by ASTM [27], there are six categories currently applied to polymers. These are vat photopolymerisation, powder bed fusion, binder jetting, material extrusion, material jetting and sheet lamination. Based on the physical state of the material before the printing process, AM processes can be further grouped into liquid-based, solid-based and powder-based technologies. Table 1 shows the classification adopted in this work, listing some of the commercial names of the AM technologies, along with the most common polymeric materials processed with each of those [22]. Vat photopolymerisation, including stereolithography (SLA), digital light processing (DLP) and the recent digital light synthesis (DLS) [28], deals with liquid resins which are cured through selective exposure to a UV light source, from either a laser or a projector. Another liquid-based technology, material jetting (such as Polyjet [29]) deposits droplets of photosensitive polymeric materials through multiple nozzles, then cured by a UV light. Powder bed fusion technologies process materials in powdered form: triggered by a heat source, commonly a low-to-medium power laser in selective laser sintering (SLS), the raw material is transformed by means of a thermal reaction. By contrast, in three-dimensional printing (3DP) powder particles are not fused but glued together by means of a liquid binding material [22]. Fused deposition modelling (FDM), the most widespread of extrusion-based AM processes, is based on printing of a continuous thermoplastic filament that is heated at the print head (nozzle) and then extruded to form, wire by wire and layer by layer, the component according to the CAD file [30]. Finally, although primarily applied to metals, sheet lamination techniques, such as laminated object manufacturing (LOM), can be used to fabricate multilayer components from polymeric sheet rolls, that are first heated and then contoured by means of laser cutting.

Table 1 Summary of the AM processes employed for the main polymeric materials

Due to the progressive shift of AM technology from fabrication of prototypes towards the production of end-use parts, the quality standards have become more stringent, demanding that the physical–mechanical properties of printed components meet in-service loading and operational requirements, in terms comparable to parts obtained from traditional manufacturing [31, 32]. A relevant aspect of AM is that the properties of the products do depend not only on the raw constituent material but also on the specific settings of the printing technology [33]. Traditionally, the influence of the printing process on the mechanical behaviour of the manufactured components has been investigated by means of empirical methods, based on the collection of a large amount of experimental data. Through accurate design of experiments (for instance, using the Taguchi method) and statistical analyses of the results, the collected information is available to derive empirical relationships and correlate the mechanical strength of the printed material with the process parameters, thus representing a valuable strategy for quality control in the manufacturing process [34]. By contrast, an approach based on a theoretical description of the printing process is recommended, in order to investigate the actual chemical–physical mechanisms occurring during the specific technology and predict the mechanical properties of the final product. Not only this could improve the production of parts with optimal properties, but also of components with tailored physical–mechanical characteristics, which is a key feature of AM applied, for instance, for developing functionally graded materials [35, 36].

In the realm of additive manufacturing of polymers, we have restricted our attention to laser-based technologies, namely SLS and SLA, both employing a laser source to either cure or melt a raw polymeric material [2]. The purpose of our work is to review the fundamentals of theoretical modelling of laser-based AM, in order to shed light on the chemical or physical variables that are more relevant for the mechanical behaviour of the printed material. In the dedicated sections of the paper, a specific attention is devoted to the binding mechanisms, which are thermally activated bonding through sintering of a powder in SLS and light-induced polymerisation of the liquid material in SLA [33]. The peculiar properties of the raw materials, the main process parameters and the relevant mechanical and physical properties of components printed with the techniques considered are also briefly discussed.

This paper is structured as follows. “Laser-based AM: technology overview, process parameters and mechanical properties” section presents an overview of the technological aspects of laser-based AM for polymers, including a short description of the properties of the raw materials, process parameters and relevant properties of the components for the single technologies. “Physical models of laser-based additive manufacturing of polymers” section forms the core of our work, where theoretical models and equations, adopted to describe the manufacturing process and characterise the mechanical behaviour of the printed material, are illustrated. In “Discussion” section, we provide a discussion on the critical aspects of modelling, with specific emphasis on its role on the mechanics of the polymeric printed components. Finally, “Concluding remarks” section is devoted to some concluding remarks and future perspectives.

Laser-based AM: technology overview, process parameters and mechanical properties

Selective laser sintering

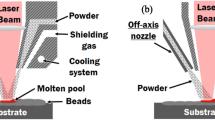
Formally ideated at the University of Texas in 1986 [37], selective laser sintering (SLS) allows complex three-dimensional parts to be built by fusing together successive layers of powdered material. A thin layer of powder, previously heated to a specific process temperature (hereinafter referred to as the pre-heating temperature), is deposited on a platform, where it is then selectively targeted by a high-power heating source, usually a CO₂ laser beam in polymer sintering, causing partial melting and densification of the particles (Fig. 1a). After finishing one layer, the platform is lowered by a pre-defined height (the layer thickness) and a new layer of powder is spread by means of an appropriate deposition system, typically a roller or a wiper blade. The sintered material forms the part, while the loose powder remains in place providing structural support to the piece. After sintering all layers, the parts and surrounding supporting material are cooled down under homogeneous conditions, the piece is extracted, and the excess powder is removed and eventually recycled for a new use [38, 39]. Laser sintering has attracted much attention because it can process a wide range of materials, including metals, waxes, ceramics and polymers, and also enabling the combination of multiple materials, such as metal–polymer powders. With respect to polymers, the predominant share is taken by semi-crystalline thermoplastics, with polyamides making up the largest part. Other processable thermoplastics include polyethylene (PE), polypropylene (PP), polycaprolactone (PCL), elastomers such as thermoplastic polyurethane (TPU), high-performance polymers such as polyetherketone (PEK) and polyetheretherketone (PEEK), and polymer blends. Amorphous polymers can be processed with SLS as well: these include polycarbonate (PC), poly(methylmethacrylate) (PMMA) and polystyrene (PS). While the range of sinterable polymeric materials is expanding, it is still limited with respect to traditional manufacturing, mainly because of an insufficient understanding of the complete relationship between raw material, process transformation and final properties. Some materials, such as PC and other amorphous polymers, offer an easy and cheap manufacturing process at the expense of poor sintering quality, and for this reason, their use is becoming less common [40]. On the other hand, high-performance polymers are sought for specific applications where exceptional mechanical, thermal and chemical resistance is required, but the high cost limits their widespread application [41].

Figure 1

a Schematic of the laser sintering set-up. b Two-dimensional illustration of the thermal process occurring in the powder bed, showing the circular moving laser beam and relevant process variables

In common with other AM technologies, SLS requires the proper setting of various parameters, such as laser power, laser diameter, scan velocity, scan spacing, build orientation and pre-heating temperature (Fig. 1b) [38], which directly affect the macroscopic characteristics of the printed parts through the interaction with the properties of the polymeric powder [40]. The importance of choosing a suitable powder should not be overlooked: in this sense, the raw material morphology, particle size distribution and surface characteristics are equally important, in order to ensure good flowability and optimal processing conditions [39,40,41,42,43]. Generally speaking, particles showing good sphericity and uniform size distribution provide better results, while poor flowability might lead to the formation of agglomerates and cause problems when spread into layers, resulting in an inhomogeneous distribution and surface defects [39]. Smaller fractions are problematic due to their faster sintering rate. Moreover, it seems they are negatively correlated with the surface roughness of the layer before sintering, due to the increased relevance of attractive interaction forces relative to particle weight [44]. Thermal properties, in particular those involved in phase transitions, are fundamental in ensuring an optimal sintering of the raw polymeric material and for the mechanical behaviour of the printed components [25]. While both amorphous and semi-crystalline polymers can be processed successfully with SLS, the role played by the different morphology needs to be taken into account [45]. Due to their broad softening range, processing of amorphous polymers only requires the pre-heating temperature to be set above the glass transition temperature. Semi-crystalline polymers should be heated close to the melting temperature, after which the material behaves like a highly viscous liquid, with crystallisation also being a critical aspect in the process. In practice, due to the hysteresis between melting and crystallisation, there appears an optimal processing window between the two transitions, commonly known as supercooling window (Fig. 2), which avoids the solidification of the material until all layers have been sintered [46]. The process of sintering is favoured by a low melt viscosity: due to their higher viscosities at processing conditions, amorphous polymers generally tend to follow a slow sintering rate, resulting in components with greater porosity [40, 47].

Figure 2

Adapted from [46]

a Scheme of the supercooling window for a typical polyamide employed in SLS, obtained from differential scanning calorimetry. b Processing temperature evolution.

The investigation of processing conditions on parts obtained from SLS has been the object of extensive experimental studies [48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64]. Part density is unanimously recognised as the principal variable affecting the mechanical behaviour of laser-sintered components. Stemming from the layered nature of AM, anisotropy is also a relevant aspect, arising because of non-uniform sintering: particles that are targeted by the laser during a single scan will in general display improved cohesion with respect to those on the adjacent scan. As a result, mechanical properties are affected by the build orientation [48, 49, 53,54,55, 59, 60]. In addition, surface roughness resulting from partially melted particles [61] is particularly critical when it comes to fatigue resistance [62, 63] and for the tribological behaviour of the components [64]. Finally, residual stresses and distortions, correlated with the thermal gradients developing in the material during both the printing process and the cooling stage, need to be considered [65].

Traditionally, the properties of printed components are related to process parameters through the influence of the surface energy density $E_{\text{b}}$ defined as the combination of laser power, scan spacing and speed $E_{\text{b}} = P /sv_{\text{b}}$ [38]. Alternatively, different definitions can be adopted, leading to the formulation of a volumetric energy density which also includes the layer thickness $d$ [49]. The so-called overlay ratio, defined as the ratio between the laser beam diameter and the scan spacing ${\text{OL}} = D_{\text{b}} /s$, has been shown to play a fundamental role on the mechanical properties of the printed components and was recently included in the definition of the surface energy density [58]. In general, all the experimental studies confirm a positive correlation of $E_{\text{b}}$ with mechanical properties such as Young’s modulus, yield stress, ultimate tensile strength and elongation at break [48,49,50,51,52,53,54,55,56,57,58,59,60] (Fig. 3). The motivation is imputed to the increased density of parts processed at high energy densities: by contrast, at lower energies the sintering process is incomplete and parts usually show a porous structure with interconnected voids [48]. However, there exists an optimal value of $E_{\text{b}}$ beyond which the porosity of the part is again increased, due to phenomena of thermal degradation, which results in the emission of gas, formation of large voids [48, 57] and change in the chemical structure of the material [51, 52]. Higher densities and better mechanical performances have also been correlated with higher pre-heating temperatures in polyamide parts. The effect seems to depend on the kinetics of crystallisation in the cooling phase: when the pre-heating temperature $T_{\text{b}}$ is kept close to the melting point, the cooling rate of the molten phase is slowed down, resulting in an increase in crystallinity [40].

Figure 3

Adapted from [48]

Dependence of the mechanical properties of printed samples on the surface energy density $E_{\text{b}}$. a Apparent part density. b Stress–strain curves. c Young’s modulus and yield stress. d Ultimate stress and elongation at break (from uniaxial tension experiments, parallel to build orientation). Material is PA12 ($P = \text{var} .,\quad v_{\text{b}} = 5.1\,{\text{ms}}^{ - 1} ,\quad s = 150\,\upmu{\text{m}})$.

Photopolymerisation

Among photopolymerisation AM processes, the earliest technique being developed is stereolithography (SLA), a chemical–physical process which converts a liquid monomer solution to a solid three-dimensional polymeric material [66], by applying UV light in a spatially controlled way according to the CAD file. Final components, which can have in general complex shapes, are built layer by layer. In the so-called top-down systems, starting from a closed vat of liquid photosensitive monomer over a platform the first layer is irradiated and cured with an assigned thickness; then, the platform moves down of a distance equal to the layer thickness, and the barely cured layer is covered with additional liquid which will also be irradiated and cured [1] (Fig. 4).

Figure 4

Scheme of the SLA set-up in top-down-based technology

Stereolithography is a very complex technology, involving more than 50 parameters for processing a single liquid monomer (which might have different chemical composition), including light intensity, curing time, post-curing time, cure depth, layer thickness, scanning velocity, to name a few [67]. Mechanical properties of the material after photopolymerisation may be poor due to incomplete conversion of the active groups [68]: for this reason, components can be subjected to a post-curing process in order to improve their strength, as shown, for example, in [69]. Raju et al. [70] have analysed the effects of layer thickness, spacing and orientation using the Taguchi method, a probabilistic technique describing the response of a system based on a reduced number of experiments, with appropriate permutations of the selected input parameters. Their study concluded that layer thickness and orientation are the main parameters influencing the mechanical properties of AM component. Specifically, a smaller layer thickness and reduced layer skewness with respect to the direction of the applied force lead to greater tensile strength. Chockalingam et al. [71] performed a similar analysis, but selecting layer thickness, building orientation and post-curing time as input parameters, and concluded that the orientation is the main factor influencing the tensile strength of the printed material. Indeed, the adhesion of the material between successive layers is generally weaker than the adhesion of the material within a single layer [72, 73]. Whereas part anisotropy is a well-consolidated aspect for other AM technologies such as FDM [33], in SLA this issue is still not unanimously acknowledged. Several authors state that build orientation slightly affects the mechanical properties of SLA components, so that components should be considered isotropic [74, 75]. For instance, Hague et al. [74] have found low variations (around 5–10%) of the elastic modulus and tensile strength for different building orientations, so that they concluded that the build orientation has little effects on the mechanical properties of the components. An additional insight in the actual chemical–physical process involved in SLA is provided by theoretical models, based, for instance, on the kinetic theory of photopolymerisation [76]. As it is shown in “Photopolymerisation” section, these models allow the identification of the most critical process parameters involved in SLA (e.g. light intensity, curing time, cure depth, etc.) and determine how these can be related to the mechanical behaviour of the manufactured part. Since the various photopolymerisation technologies currently available share the same basic principle of SLA, the purpose of “Photopolymerisation” section is to focus on the common chemical–physical process of light-induced polymerisation which applies to all of them.

Physical models of laser-based additive manufacturing of polymers

Selective laser sintering

Selective laser sintering is characterised by three main distinct processes: (1) powder spreading, (2) absorption of the laser energy and heat transfer within the powder bed and (3) sintering and cooling of the polymeric material (Fig. 1b) [40]. This section reviews the fundamentals of theoretical modelling applied to SLS in polymeric materials, with specific emphasis on the physical aspects of the transformation that are more relevant for the mechanical behaviour of the parts. Although the stage of powder recoating has been shown to have some consequences on processing, this is not included in the following part, and the reader is referred to the considerations outlined in “Selective laser sintering” section and the dedicated literature [40,41,42].

In the subsequent stages of SLS, the powder undergoes multiple phase transitions, each of them accompanied by both absorption and release of thermal energy, during which the material properties change drastically as a result of temperature fluctuations. Given the problem nonlinearities, numerical solution methods have been used extensively, with an important distinction based upon the modelling scale. The traditional approach is to simulate the powder mass as a homogeneous porous medium, so that the governing equations are derived from the conservation of energy applied to an arbitrary control volume. Classical numerical methods such as finite elements (FE), finite differences or finite volumes can then be used [77]. The alternative is to model the granular nature of the material and describe heat conduction in a heterogeneous system made of solid particles and voids. Particle-based methods, such as the discrete element method (DEM), seem promising although their computational costs made their use far less common [78].

We begin in “Models of the thermal process” section by considering the thermal problem, following the schematic distinction between the optical sub-model, characterising the energy absorption in the powder bed, and the heat transfer sub-model, as proposed in the groundwork of Sun and Beaman [79]. The stage of sintering is described in detail in “Models of the sintering process” section, focusing on both the micro-mechanical models and the continuum-based description. As the particles are heated and coalesce, the density of the powder bed, as well as the thermal properties, changes; therefore, the sequential order in which the stages are presented should not be viewed as a possibility of separating them. On the contrary, the mechanical behaviour is often analysed separately, through an uncoupled approach; that is, the thermal problem is solved at once; then, its results become inputs for the mechanical analysis [77]. Considerations regarding the mechanical behaviour of the printed material are included in “Models of the mechanical behaviour” section. A summary of the models reviewed is presented in Table 2.

Table 2 Summary of the works reviewed on analytical modelling of SLS for polymers

Models of the thermal process

Models of the thermal process in SLS belong, in general, to the family of three-dimensional unsteady heat transfer problems. Firstly, we consider the optical sub-model, describing the laser energy deposition in the powder bed, based on the interaction between the electromagnetic radiation and the optical properties of the material. In laser-based manufacturing, the amount of absorbed energy is responsible for heating and densification of the material. Most of the available models of SLS are developed on a simplifying assumption, where the powder bed is treated as a homogeneous material, with effective optical properties obtained from experiments. However, it was observed that powders have larger absorptance compared to a solid of the same material [97] and should be represented as a granular semi-transparent medium, where the mechanics of laser-particle interaction is affected by absorption, scattering and internal emission [93].

The recurring approach is to assume a radial Gaussian distribution of the laser intensity on the powder surface. Supposing that the laser scans the horizontal $xy$ lane with uniform velocity $v_{\text{b}}$ (Fig. 1c), the expression for the light intensity over the irradiated surface is [79]

$$I\left( {x,y,t} \right) = I_{0} \exp \left\{ { - \,\,c\left[ {\left( {x - v_{\text{b}} t} \right)^{2} + \left( {y - v_{\text{b}} t} \right)^{2} } \right]} \right\}$$

(1)

where $c$ is a concentration coefficient, depending on the characteristic distribution of the radiation. For instance, if one considers a circular spot of radius $w_{\text{b}}$ where 85% of the light intensity is absorbed, then the concentration factor is $c = 2 /w_{\text{b}}^{2}$ [80]. The maximum light intensity $I_{0}$ in the centre of the laser spot is related to the laser power through $I_{0} = Pc /\pi.$

In a semi-transparent homogeneous medium, the attenuation of laser radiation with depth is provided by an extinction coefficient, following the well-known Beer–Lambert’s law. The heat flux density per unit volume is then given by [79]

$$q_{\text{b}} \left( {x,y,z,t} \right) = \left( {1 - R_{\text{R}} } \right) e_{\text{R}} I_{0} \exp \left\{ { - c\left[ {\left( {x - v_{\text{b}} t} \right)^{2} + \left( {y - v_{\text{b}} t} \right)^{2} } \right] - e_{\text{R}} z} \right\}$$

(2)

where $e_{\text{R}}$ is proportional to the inverse of the powder particle size and $\left( {1 - R_{\text{R}} } \right)$ represents the absorptance of the polymeric material.

Shortcomings of the continuum-based approach have been clearly reported in the literature, stemming from the fact that the relevant transparency of granular materials is neglected [93, 94]. A more accurate description is achievable by considering micro-scale models of the powder bed. Through ray-tracing algorithms, the trajectories of the light rays, or photons, emitted by the laser source can be simulated probabilistically when travelling into the considered medium, until they hit a pre-defined area. According to the model proposed by Xin et al. [93], the initial position of a photon in the laser beam section is defined in spherical coordinates by the radius and the azimuthal angle $\varphi$, where the angle is distributed uniformly in the interval $\left[ {0, 2\pi } \right]$, while the radius follows the usual Gaussian distribution inside the laser spot (Fig. 5a). The displacement of each photon in the medium is calculated probabilistically, as a function of absorptance and scattering coefficients of the material. Under the assumption of spherical particles, the scattering direction of incident photons is independent of the azimuthal angle, while the longitudinal angle $\vartheta$ is obtained from [93]

$$\cos \vartheta = \frac{1}{2g}\left[ {1 + g^{2} - \left( {\frac{{1 - g^{2} }}{1 - g + 2g\xi }} \right)^{2} } \right]$$

(3)

where $g$ is an anisotropy factor and $\xi$ is a pseudo-random number uniformly distributed in the interval [0, 1]. Moreover, the probability that light is internally reflected or transmitted is computed by comparing the pseudo-random number with Fresnel’s reflection coefficient $R\left( {\vartheta_{\text{i}} } \right)$ where $\vartheta_{\text{i}}$ is the angle of incidence at the boundary (Fig. 5a). The angle of the transmitted ray $\vartheta_{\text{t}}$ is given by Snell’s law, $n_{\text{i}} \sin \vartheta_{\text{i}} = n_{\text{t}} \sin \vartheta_{\text{t}}$, with $n_{\text{i}}$ and $n_{\text{t}}$ representing the incident and transient refraction coefficients, respectively.

Figure 5

Adapted from [93]

a Two-dimensional sketch of the ray-tracing model, including transparency and scattering. b Distribution of scattered photons in the powder bed. The dashed lines are the boundaries without scattering. c Distribution of the normalised heat flux, at various depths, with and without scattering (diamonds include scattering). Material is a polyamide (PA12) powder ($P = 10\,{\text{W}},\,\,\, a = 5\,\upmu{\text{m}},\,\, w_{\text{b}} = 50.8\,\upmu{\text{m}},\,\,R_{\text{R}} = 0.04,\,\,e_{\text{R}} = 20\,{\text{mm}}^{ - 1} ,\,\, g = 0.93$).

Due to scattering, the heat flux on the surface is wider than the area of the laser source and then shrinks with increasing depth, leading to a heated zone at the surface that is larger than at the bottom (Fig. 5b). This fact is clearly illustrated in Fig. 5c, through a comparison of the volumetric heat density obtained from the ray-tracing model and that predicted by the traditional Beer–Lambert’s attenuation law, as shown in Eq. (2). The results are normalised with respect to the maximum emitted flux. With scattering, the width of the sintered region appears to be larger, but depth is reduced due to the fact that photons are not propagated uniformly in the longitudinal direction [93].

Due to the energy coming from the laser and the pre-heating temperature of the processing chamber, heat transfer occurs in the powder bed, including phenomena of conduction, convection and radiation. Through the well-known equation of heat conduction, written in a general three-dimensional framework, we have [79]

$$\rho c_{\text{p}} \frac{\partial T}{\partial t} = \nabla \cdot \left( {\lambda \nabla T} \right) + q_{\text{g}}$$

(4)

where $\nabla T$ is the temperature gradient and $q_{\text{g}}$ is the term of volumetric heat generation. Standard boundary conditions, accounting for energy losses through radiation and convection on the powder bed surface, have to be considered [79]. The effective thermo-physical properties included in the equation are usually obtained through mixing laws, as a function of the solid and gas fractions of the powder mass. For the density, specific heat and thermal conductivity, we have [80]

$$\rho = \left( {1 - \phi } \right)\rho_{\text{S}} + \phi \rho_{\text{G}} ,\quad c_{\text{p}} = \frac{1}{\rho }\left[ {\left( {1 - \phi } \right)\rho_{\text{S}} c_{\text{p,S}} + \phi \rho_{\text{G}} c_{\text{p,G}} } \right],\quad \lambda = \left( {1 - \phi } \right)\lambda_{\text{S}} \frac{1}{{1 + C \frac{{\lambda_{\text{S}} }}{{\lambda_{\text{G}} }}}}$$

(5)

where $C$ is a coefficient depending on the relative density. Both specific heat and thermal conductivity are strongly affected by temperature variations; in particular, the specific heat is found to follow a linear increasing trend, with a step change corresponding to the glass transition [80].

The volumetric term $q_{\text{g}}$ in the heat equation, as shown in Eq. (4), accounts for different contributions, depending on the material and the specific stage of the thermal process [95]. As the temperature increases, amorphous materials pass the glass transition, which as a second-order phase transformation implies relevant changes in the heat capacity but is not related to any latent heat. On the contrary, melting and crystallisation occurring in semi-crystalline polymers also require careful consideration of the related enthalpy, so that we can write $q_{\text{g}} = q_{\text{b}} + s_{\text{f}} + s_{\text{c}}$ [95]. From the relationships for phase change systems, the heat sink related to melting can be expressed as $s_{\text{f}} = - \left( {1 - \phi } \right)\Delta h_{\text{f}} \partial f_{\text{L}} /\partial t$, where $\Delta h_{\text{f}}$ represents the total latent heat of fusion and $f_{\text{L}}$ is the liquid fraction [95], while the source term related to crystallisation depends on the degree of crystallisation $\alpha$ (defined as the ratio of the crystallised volume to the ultimate crystallisable volume) according to $s_{\text{c}} = \rho_{\text{c}} \Delta h_{\text{c}} \partial \alpha /\partial t$ [98]. Adequate models are needed to describe the kinetics of crystallisation and the evolution of thermal properties during the process. For non-isothermal processes, Nakamura’s model provides the following law for the rate of crystallisation as a function of temperature [99]

$$\frac{\partial \alpha }{\partial t} = n_{\text{c}} K\left( T \right)\left( {1 - \alpha } \right)\left[ {\ln \left( {\frac{1}{1 - \alpha }} \right)} \right]^{{\frac{{n_{\text{c}} - 1}}{{n_{\text{c}} }}}}$$

(6)

where $n_{\text{c}}$ is the Avrami index, $\alpha$ is the relative mass crystallinity, depending on the geometry of crystallites, and $K\left( T \right)$ is Nakamura’s non-isothermal nucleation rate. The reader is referred to the dedicated literature for additional information on the topic, e.g. [100, 101]. During the crystallisation stage, the effective thermo-physical properties defined in Eq. (5) are replaced by

$$\begin{aligned} & \rho_{\text{c}} = \alpha \rho_{\text{S}} + \left( {1 - \alpha } \right)\rho_{\text{L}} \\ & c_{\text{p,c}} = \alpha c_{\text{p,S}} + \left( {1 - \alpha } \right)c_{\text{p,L}} \\ & \lambda_{\text{c}} = \alpha \lambda_{\text{S}} + \left( {1 - \alpha } \right)\lambda_{\text{L}}. \\ \end{aligned}$$

(7)

In practice, if the processing temperature is kept within the optimal window $\Delta T = \left( {T_{\text{m}} - T_{\text{c}} } \right)_{\text{in}}$ (Fig. 2b), the volumetric heat flux $q_{\text{b}}$ and the heat sink $s_{\text{f}}$ can appear at the same time, whereas crystallisation takes place during the cooling stage. However, it is worth mentioning that partial crystallisation might also occur throughout the process, when the material heated by the laser source cools down to the chamber temperature [40].

From three-dimensional FE simulations of SLS in a polyamide powder, Mokrane et al. [95] obtained accurate temperature maps in the powder bed, also showing the thermal influence of adding new layers on top of each other. The results presented in Fig. 6 are obtained from the solution of the thermal process combined with a sintering model, as described in the following section. From Fig. 6c, it is evident that the addition of a new layer causes a temperature drop at the interface of about 50 K, a fact that could alter the expected kinetics of crystallisation within the quasi-isothermal processing window shown in Fig. 2a. Recent experiments confirmed that the minimum layer temperature during powder recoating can drop below the crystallisation temperature $T_{\text{c,in}}$ [46]. Further results on the role of crystallisation and how it is influenced by the SLS process parameters can be found in the work by Amado [91].

Figure 6

Adapted from [95]

a Surface temperature distribution in the first layer (top view of the layer). b Temperature distribution in the vertical cross section (xz plane), when adding the second layer. c Temperature distribution in the vertical cross section (yz plane) at the end of the process. Material is PA12, with $T_{\text{m}} = 461^\circ{\text{K}}$, $T_{\text{c}} = 454^\circ {\text{K}}$ and layer thickness d = 200 μm ($P = 45\,{\text{W}},\,\,v_{\text{b}} = 15\,{\text{ms}}^{ - 1} ,\,\,s = 150\,\upmu{\text{m}}$).

Models of the sintering process

Sintering is the term commonly used to describe the transformation through which a powdered material is converted into a porous solid. The purpose of this paragraph is to elucidate its role within the SLS manufacturing process, by reviewing some fundamental models proposed for glass, ceramics and polymers. The reader can find an in-depth presentation of the physics of sintering and densification in the work by Kruth et al. and references therein [102].

In polymeric powders, sintering occurs by means of various mechanisms, including liquid-phase sintering with partial melting, consolidation at the glass transition temperature, polymer chain rearrangement and cross-linking [103]. Solid-state sintering is not relevant, due to the high velocity of the laser, which does not allow sufficient time for diffusion of atoms in the solid state to occur [102]. During SLS, densification occurs in non-isothermal conditions within a large volume of material, inducing global consolidation of the powder that can lead to the formation of large voids [104, 105]. The polymer viscosity changes with temperature according to an exponential Arrhenius’ law, given by $\eta = \eta_{0} \exp \left( {\frac{\Delta E}{RT}} \right)$, so that the rate of densification is expected to vary exponentially with temperature. In continuum-based modelling of SLS, it is recurring practice to describe sintering in terms of the change with time of the apparent density of the material (or through the specular variation of the void fraction), according to the following empirical expression [83]

$$\frac{\partial \rho }{\partial t} = A\exp \left( { - \frac{\Delta E}{RT}} \right)\left( {\rho_{\infty } - \rho } \right) = K_{\text{s}} \left( T \right)\left( {\rho_{\infty } - \rho } \right)$$

(8)

where $\rho_{\infty }$ is the theoretical density achievable in an infinitely long sintering time [83]. $K_{\text{s}} = A \exp \left( { - \Delta E /RT} \right)$ represents a temperature-dependent densification parameter, expressed as a function of the activation energy and the Arrhenius’ coefficient $A$. In semi-crystalline polymers, the crystallinity content is known to affect the viscous behaviour by reducing the mobility of the polymer chains [43]; thus, the activation energy can be increased by means of a correction proportional to the crystalline fraction of the material [85].

Throughout the years, there have been several analytical models, proposed to describe sintering of polymers and other materials, which are worth mentioning. Furthermore, using particle-based numerical methods, such as the DEM, it is possible to directly model the interaction between a large number of particles based on a micro-mechanical description of sintering. This approach, adopted, for instance, to describe sintering in metallic and glass materials under different conditions [106,107,108], has recently been included in models for SLS of polymers [93]. Sintering of polymeric powders evolves through two consecutive stages of densification [109]: (1) coalescence of the powder particles and (2) densification of the molten mass (Fig. 7a). In the first stage, polymeric particles heated above their glass transition or melting temperatures are forced to coalesce through the formation of necks, in order to decrease their total surface area. According to the classical theory of sintering, the work done by surface tension is opposed to the energy dissipated by viscous flow, while the effect of gravity is neglected. Analytical models were developed for isothermal sintering of amorphous materials, which approximately behave as Newtonian fluids. Although polymers exhibit a pseudo-plastic melt flow, it is argued that during sintering shear rates are extremely low so that in practice the flow remains Newtonian [109].

Figure 7

a Two-dimensional scheme of the densification process in a polymeric powder bed. b Frenkel’s model describing the coalescence of two spherical particles [110]. c Scherer’s model [117]

Considering the coalescence of two identical incompressible spherical particles of initial radius $a_{0}$ (Fig. 7b), Frenkel’s model provided the fundamental law for the time evolution of the neck radius $l$, given by [110]

$$\left( {\frac{l}{a}} \right)^{2} = \frac{\gamma }{{\eta a_{0} }}t.$$

(9)

When compared to experimental results, Frenkel’s model overestimates the sintering rate, except at the very beginning of the coalescence process, and predicts a sintering force acting on the particles that is independent of time [111]. Indeed, particles evolve without preserving the same shape, a fact that prompted Pokluda et al. [112] to modify Eq. (9) by including the evolution of the sintering angle $\theta \left( t \right)$ (Fig. 7b). Further modifications to Frenkel’s model pointed at the limitations of the Newtonian flow assumption, observing that the measured coalescence rate in semi-crystalline materials is often lower than predicted. This might also depend on shrinkage of individual particles before melting, which causes a delay in the coalescence rate [113]. Bellehumeur et al. [114] proposed an integration of the term related to viscous dissipation in order to include the viscoelastic behaviour of polymers. The sintering angle is derived by solving numerically the following equation:

$$8\left( {m \tau c_{1} \frac{\partial \theta }{\partial t}} \right)^{2} + \left( { - 2m \tau c_{1} + \frac{{\eta a_{0} }}{\gamma }\frac{{c_{1}^{2} }}{{c_{2} }}} \right)\frac{\partial \theta }{\partial t} - 1 = 0$$

(10)

where $\tau$ is the time of viscous relaxation, the coefficient $m = 1$ if an upper-convected Maxwell model is assumed and $c_{1} , c_{2}$ depend on the sintering angle $\theta \left( t \right)$ [114]. According to this model, faster coalescence rates are predicted in materials with a lower characteristic relaxation time. Recent modifications by Balemans et al. include the extension to more complex viscoelastic models [115] and time-dependent viscosity under the effect of the thermal boundary conditions of SLS [116]. As an alternative to the model of spherical particles, Scherer [117, 118] proposed an approximation of the porous material with cubic cells containing intersecting cylinders, whose radius corresponds to the average particle size (Fig. 7c), and derived the time evolution of the aspect ratio of cylinders as $\partial x_{\text{c}} /\partial t = \gamma /\left( {2\eta L_{\text{c}} } \right)$, with $x_{\text{c}} = a /L_{\text{c}}$ [117].

Models based solely on viscosity and surface tension phenomena can describe satisfactorily the process until the condition of isolated pores is attained. Interestingly, Scherer [117] provided an upper limit for the validity of this class of models, which is attained when the relative density of the powder exceeds 0.94 (in his model, this corresponds to an aspect ratio of cylinders $x_{\text{c}} = 0.5$, Fig. 7c). In the second stage of sintering, densification of the molten mass proceeds through the collapse of the pores, or air bubbles, entrapped in the melt. As such, different models, describing the bubble shrink and subsequent diffusion of the dissolved gas into the surrounding melt, are required [109]. The earliest description is the model of bubble dissolution proposed by Mackenzie et al. [119], which approximates the process of densification to the shrinking of a spherical bubble in an incompressible viscous continuum. Models considering the pressure of the air entrapped in the pores were later proposed [120, 121].

It appears convenient to put in connection the micromechanics of sintering described by the analytical models to the apparent density, as defined in Eq. (8). Following Scherer [117], we can introduce an isothermal densification coefficient $K_{\text{s}}$, depending on the physical properties that are relevant in the process of sintering and on the microstructure of the powder bed. For models of viscous sintering, this coefficient can be written as $K_{\text{s}} = \left( {\gamma n_{\text{G}}^{ 1 / 3} } \right) /\eta$, where $n_{\text{G}}$ represents the number of pores per unit volume, to be obtained from experimental analyses of the powder microstructure [117]. We are now able to compare the evolution of the apparent density in terms of a dimensionless densification time $\bar{t}_{\text{s}} = K_{\text{s}} \left( {t - t_{0} } \right)$ [122], where here $t_{0}$ is an initial fictitious time. Similar relationships can be established in terms of the evolution of the void fraction $\phi$ [123].

For the stage of part coalescence, we first need to correlate the neck growth rate to the variation of part density. From Frenkel’s model [110], the predicted densification rate is described by the following expressions

$$\begin{aligned} & n_{\text{G}} = \frac{3}{{4\pi r_{0}^{3} }}, \quad \frac{\Delta L}{{L_{0} }} \simeq \left( {\frac{l}{2a}} \right)^{2} = \frac{1}{4}\frac{\gamma }{{\eta a_{0} }}t = 1 - \left( {\frac{{\rho_{0} }}{\rho }} \right)^{1/3} \\ & \bar{t}_{\text{s}} = 4\left( {\frac{3}{4\pi }} \right)^{1/3} \left[ {1 - \left( {\frac{{\rho_{0} }}{\rho }} \right)^{1/3} } \right] \\ \end{aligned}$$

(11)

where $\Delta L = L\left( t \right) - L_{0}$, $L_{0}$ is the initial distance between the centres of the spheres (notice that it might be smaller than the particle radius due to a small initial angle $\theta_{0}$, Fig. 7b) and $\rho_{0}$ is the initial density. From Scherer’s model, we find instead [118]

$$\begin{aligned} & n_{\text{G}} = \left( {\frac{{\rho_{0} }}{{\rho_{\text{S}} }}L_{{{\text{C}},0}} } \right)^{ - 1} ,\quad \frac{{L_{\text{C}} }}{{L_{{{\text{C}},0}} }} = \frac{{\rho_{0} }}{{\rho_{\text{S}} }}\left( {3\pi x_{\text{c}}^{2} - 8\sqrt 2 x_{\text{c}}^{3} } \right)^{ - 1} \\ & \overline{{t_{\text{s}} }} = 2\int\limits_{{x_{{{\text{c}},0}} }}^{{x_{\text{c}} }} {(3\pi - 8\sqrt 2 x_{\text{c}} )^{ - 1/3} \chi_{\text{c}}^{{ - 2/3d\chi_{\text{c}} }} }. \\ \end{aligned}$$

(12)

For the following stage of bubble dissolution, the model by Mackenzie et al. [119] can also be described through the same densification parameter $K_{\text{s}}$, as the only relevant quantities are surface tension and viscosity. The densification rate is given by [119]

$$\overline{{t_{\text{s}} }} = \frac{2}{3}\left( {\frac{3}{4\pi }} \right)^{1/3} \frac{1}{{\rho_{\text{S}} }}\mathop \int \limits_{{\rho_{0} }}^{\rho } \left( {1 - \frac{\rho }{{\rho_{\text{S}} }}} \right)^{ - 2/3} \left( {\frac{\rho }{{\rho_{\text{S}} }}} \right)^{ - 1/3} {\text{d}}\rho.$$

(13)

The predicted densification rates are compared in Fig. 8 with experimental data from sintering of rotational moulding grade polymers [122].

Figure 8

Adapted from [122]

Relative density as a function of the dimensionless sintering time $\bar{t}_{\text{s}}$ for various analytical models. Experimental data come from isothermal sintering experiments, for low-density polypropylene (PE) and ethylene–butyl–acrylate (EBA), a low-crystallinity polyethylene copolymer with high viscosity.

Models of the mechanical behaviour

Considering the processes described so far, it appears that several mechanisms might affect the mechanical properties of laser-sintered components. Unfortunately, only a limited number of investigations, concerning with analytical modelling of SLS, were devoted to the description of the mechanical behaviour through the solution of the coupled thermo-mechanical problem. As anticipated in “Selective laser sintering” section, part porosity is unquestionably the key factor influencing the mechanical behaviour of printed parts, with respect to elastic and ultimate properties. Part anisotropy, surface roughness and thermal-induced residual stresses are additional issues of SLS that impact negatively on the mechanical performance of the printed components [124]. It is out of the scope of this work to review the vast literature on mechanical models for the behaviour of thermoplastics or porous materials. In this section, we restrict our attention to those models that were specifically considered for polymeric parts produced by SLS, leaving further and more general considerations to “Discussion” section.

When subjected to stress, thermoplastic polymers display a time- and temperature-dependent behaviour and eventually fail according to a ductile mechanism, that is, from the accumulation of plastic deformation in time. With respect to purely amorphous polymers, the deformation related to the crystalline phase needs to be considered in material models of semi-crystalline polymers, and this can be achieved by decomposing the deformation according to an appropriate rheological scheme. To describe the uniaxial tension and compression of polyamide 12 (PA12) specimens fabricated by SLS, Schneider and Kumar [125] adopted a three-network material model suitable to describe the thermoviscoplastic behaviour of polymers below the glass transition temperature. This model consists of three different spring-dashpot elements arranged in parallel (Fig. 9a): networks A and B are defined by a temperature-dependent Arruda–Boyce eight-chain model [126] in series with a viscoplastic dashpot (note that the stiffness of network A should be lower than that of B); network C consists of a hyperelastic spring based on the eight-chain model with linear dependence on the second strain invariant. The experimental and simulated stress–strain curves are illustrated in Fig. 9b.

Figure 9

Adapted from [125]

a Rheological scheme of the three-network thermoviscoplastic model. b Stress–strain tensile and compressive response of PA12 specimens ($T = 20\,^\circ {\text{C}},\,\,\dot{\varepsilon } = 0.003\,{\text{s}}^{ - 1}$).

Paolucci et al. [127] have recently focused on the ductile failure of PA12 laser-sintered specimens, using a modified form of Ree–Eyring activated flow theory [129, 130] to describe the rate- and temperature-dependent yield stress, which is given as

$$\sigma_{\rm y} \left( {\dot{\varepsilon },T} \right) = \frac{{\kappa_{\text{B}} T}}{{V_{1}^{*} }}\sinh^{ - 1} \left[ {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0,1} }}\exp \left( {\frac{{\Delta E_{1} }}{RT}} \right)} \right] + \frac{{\kappa_{\text{B}} T}}{{V_{2}^{*} }}\sinh^{ - 1} \left[ {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0,2} }}\exp \left( {\frac{{\Delta E_{2} }}{RT}} \right)} \right]$$

(14)

where $\dot{\varepsilon }$ is the strain rate, $V^{*}$ is the activation volume, $\dot{\varepsilon }_{0}$ is the rate factor and the subscripts 1,2 are related to intralamellar and interlamellar deformation, respectively [127]. In Fig. 10a, the yield stress of the material is shown for different strain rates and temperatures. The change in slope is due to the activation of the different mechanisms in the polymer’s structure. Comparing the yield stress of specimens obtained from compression moulding and SLS, it appears that a relevant gap exists at high applied strain rates and temperatures below the glass transition. It is speculated that the reduced yield stress of laser-sintered components is ascribable to their higher degree of crystallinity, as below $T_{\text{g}}$ it is the interlamellar amorphous fraction that mainly contributes to the strength of the material. The same model has also been used to account for the influence of humidity, which is known to reduce the glass transition temperature of the polymer, replacing $T$ in Eq. (14) with an apparent temperature $T^{'} = T + \left( {T_{\text{g}} - T_{\text{g,wet}} } \right)$ [131]. In practice, the effect in terms of mechanical properties is analogous to an increase in the ambient temperature [127].

Figure 10

Tensile behaviour of PA12. a Yield stress of moulded and SLS samples, at different temperatures and strain rates. The wet case is for a relative humidity of 75%. (Dots are experimental data from tensile tests and lines are model fitting.) Adapted from [127]. b Stress–strain curve of PA12 tensile specimens ($T = 23\,^\circ {\text{C}},\,\,\dot{\varepsilon } = 0.001\,{\text{s}}^{ - 1} ,\,\,\,\sigma_{\text{y}} = 17.5\, {\text{MPa}}, \,\,\phi_{0} = 0.047$). Comparison of experimental data with model fitting: viscoplastic and viscoplastic + GTN’s model. Adapted from [134]

Schob et al. [134, 135] employed a Gurson–Tvergaard–Needleman (GTN) damage model [136, 137] to simulate the behaviour of tensile PA12 specimens under static and cyclic loading (Fig. 10b). The viscoplastic behaviour of the polymer accounts for void growth and coalescence, according to the following yield function

$$\psi \left( {\varvec{\sigma},\sigma_{\rm y} ,\phi } \right) = \left( {\frac{{\sigma_{\text{VM}} }}{{\sigma_{\rm y} }}} \right)^{2} + 2q_{1} \phi^{*} \cosh \left( {\frac{3}{2}q_{2} \frac{{\sigma_{\text{h}} }}{{\sigma_{\rm y} }}} \right) - \left( {q_{3} \phi^{{*^{2} }} + 1} \right) = 0$$

(15)

where $\sigma_{\text{VM}}$ is the equivalent von Mises stress, $\sigma_{\text{h}} = \text{tr}\varvec{\sigma}$/3 is the hydrostatic stress, $\phi^{*} \left( \phi \right)$ is the modified void fraction of and $q_{1} ,q_{2} , q_{3}$ are temperature-dependent parameters of the GTN’s model.

Thermal gradients developing in the material during the AM process are among the main sources of part inaccuracy. In order to predict the expected warping of polymeric parts obtained from SLS, Ganci et al. [92] adopted an elastoplastic constitutive relationship to study the influence of thermal gradients developing into the printed material (polypropylene) during cooling. However, Amado et al. [91] observed that not only the temperature gradient but also the inhomogeneous crystallisation might contribute to the material shrinkage in thermoplastics. During the cooling stage, the heat transfer is governed by the following specific form of the general Eq. (4)

$$\rho_{\text{c}} c_{\text{p}} \frac{\partial T}{\partial t} = \nabla \cdot \left( {\lambda_{\text{c}} \nabla T} \right) + \rho_{\text{c}} \cdot h_{\text{c}} \frac{\partial \alpha }{\partial t}$$

(16)

where the crystallisation kinetics and the effective physical properties of the material are given in Eqs. (6)–(7). The mechanical behaviour of the polymer is described by a generalised viscoelastic Maxwell model, where the relaxation times of each branch are shifted according to a time-crystallisation-temperature superposition, following the approach adopted for cross-linked polymers [132, 133]. The relaxation modulus of the material during the crystallisation is written as

$$\mu \left( {t,\alpha ,T} \right) = \mu_{\infty } + \mathop \sum \limits_{\text{i}} \mu_{\text{i}} \left( {\alpha_{\text{ref}} ,T} \right)\exp \left( { - \frac{t}{{A_{\text{C}} \left( {\alpha ,T} \right)\tau_{\text{i}} }}} \right)$$

(17)

being $\alpha_{\text{ref}}$ the reference degree of crystallisation and $A_{\text{C}} \left( {\alpha ,T} \right)$ the shift function [91].

Recently, Li et al. [128] proposed a thermo-mechanical model to accurately predict residual stresses, shrinkage and warping of polymeric parts (polyamide PA-12). With respect to the previous models, they included both the heating and cooling steps in a numerical finite element model, and accounted for the recrystallisation-induced strains in the material. Specifically, the polymeric material was modelled as an elastic–plastic solid, where the strain increment is expressed as ${\text{d}}\varepsilon = {\text{d}}\varepsilon^{\text{e}} + {\text{d}}\varepsilon^{\text{p}} + {\text{d}}\varepsilon^{\text{T}} + {\text{d}}\varepsilon^{\text{c}}$, with the superscripts denoting, respectively, the elastic, plastic, thermal and crystallisation strain increment. The latter can be related to the relative crystallinity through Eq. (6).

Photopolymerisation

Photopolymerisation is based on a chemical–physical reaction where a UV light triggers free radical polymerisation. At the first step of the reaction, the liquid resin monomer $M$ is irradiated by the light; thus, photo-initiators molecules $\beta$ placed inside the resin are converted into free radicals $R^{ \cdot }$. In the second step, free radicals react with monomer molecules providing the activation of the functional groups $P^{ \cdot }$, which are polymer chains able to propagate by reacting with other monomer molecules. Then, these polymer chains propagate or cross-link with other polymer chains until a termination stage is reached; such a stage occurs when two functional groups react with each other to give a dead polymer chain $P_{\text{dead}}$, i.e. when two polymer chains connect together, or when a functional group react with a free radical. A simple reaction scheme is reported in Eq. (18) and is described in depth in [138,139,140,141,142], while a sketch of this photopolymerisation process is depicted in Fig. 11.

$$\begin{aligned} & {\text{Photo}}-{\text{initiators}}\,{\text{decomposition}}:\beta \mathop \to \limits^{{k_{\text{d}} }} 2R^{ \cdot } \\ & {\text{Initiation}}\,{\text{of}}\,{\text{a}}\,{\text{polymer}}\,{\text{chain}}:R^{ \cdot } + M\mathop \to \limits^{{k_{\text{p}} }} P^{ \cdot } \\ & {\text{Propagation}}\,{\text{of}}\,{\text{a}}\,{\text{polymer}}\,{\text{chain}}:P^{ \cdot } + M\mathop \to \limits^{{k_{\text{p}} }} P^{ \cdot } \\ & {\text{Termination}}: \begin{array}{*{20}l} {P^{ \cdot } + P^{ \cdot } \mathop \to \limits^{{k_{\text{t}} }} P_{\text{dead}} } \hfill \\ {P^{ \cdot } + R^{ \cdot } \mathop \to \limits^{{k_{\text{t}} }} P_{\text{dead}} }. \hfill \\ \end{array} \\ \end{aligned}$$

(18)

In the above expressions, $k_{\text{d}}$, $k_{\text{p}}$ and $k_{\text{t}}$ are the rate constants. In the initial stage of the process (i.e. when only liquid resin is present in the vat), the degree of cure is $\varrho = 0$; as the reaction proceeds, $\varrho$ increases in time because of the polymer chains growth.

Figure 11

Scheme of the photopolymerisation reaction; at the initial state (monomer in a liquid phase), the contained photo-initiators are in the inactive state. As the resin is irradiated by the UV light, photo-initiators are converted to free radicals which react with monomer molecules in order to provide polymer chains growth, whose amount is quantified by the degree of cure $\varrho = \varrho \left( t \right)$

The degree of cure achieved during the photopolymerisation process chiefly affects the mechanical behaviour of the printed component. Early models analysed the problem from an energetic point of view, assuming that the cure process begins only when a critical value of energy, a material-dependent parameter, is reached [143, 144]. The resin is assumed to be cured (i.e. the polymer network has formed) when the irradiated energy into the resin attains a threshold value. Recently developed models are aimed at describing the photopolymerisation reaction from a kinetic point of view in order to predict the evolution of the cure parameter in time, $\varrho = \varrho \left( t \right)$. Differently from the energetic approaches, kinetic models are able to distinguish different degrees of cure, which in turn affect the mechanical properties of the polymer. In other words, in order to correctly predict the mechanical performance of the component, it is not sufficient to determine whether curing is achieved or not but having knowledge of the degree of cure achieved. In a mechanistic approach, the degree of cure is evaluated by solving several partial differential equations describing the evolution (in time and, depending on the model, also in space) of one or more reactant variables involved in the curing process. This approach typically requires a large number of parameters, generally obtained from experimental data fitting, in order to be solved, so that this problem is often intractable and it is not useful for engineering purposes [145]. The phenomenological approach simplifies the simulation of the AM process by describing the whole curing phenomenon, i.e. all the reactions reported in Eq. (18) by means of a single differential equation of the form:

$$\frac{{{\text{d}}\rho }}{{{\text{d}}t}} = K_{\text{P}} \left( T \right) f\left( \varrho \right)$$

(19)

where $K_{\text{P}}$ is a chemical-controlled rate constant and $f$ is a function of the degree of cure. This approach, usually requiring a limited number of parameters, is suitable for engineering applications.

In the following, several models describing the cure degree evolution are presented. A summary of the models reviewed is presented in Table 3. We have included in this table all the studies focusing on the curing evaluation, irrespectively whether they are related or not to the mechanical properties of the printed component.

Table 3 Summary of the theoretical models analysed for cure prediction in photopolymerisation

Coupled photo-thermal phenomenological kinetic model

A coupled photo-thermal kinetic model, which describes both the irradiation mechanism and the exothermic characteristics of the curing reaction, has been proposed by Bartolo [146, 147]. The phenomenological kinetic approach used within this model describes the evolution of the degree of cure as follows:

$$\frac{{{\text{d}}\varrho }}{{{\text{d}}t}} = \frac{1}{{1 + { \exp }\left[ {\zeta \left( {\varrho - \varrho_{\text{d}} } \right)} \right]}} K_{{{\text{P}},0}} \,\,\, I^{\text{p}} \exp \left( { - \frac{\Delta E}{RT}} \right) \left[ \beta \right]^{q} \varrho^{m} \left( {1 - \varrho } \right)^{n}$$

(20)

where $\varrho_{\text{d}}$ is the critical value of the degree of cure corresponding to the onset of diffusion-controlled effects over the curing reaction, $\zeta$ is the diffusion constant, $K_{{{\text{P}},0}}$ is the pre-exponential factor of the rate constant, $I$ is the light intensity evaluated from Eq. (21), $p$, $q$ are constants and the exponents $m$, $n$ represent the reaction orders [147].

In this model, the kinetic parameters $\zeta$, $\varrho_{\text{d}}$, $m$, $n$ and $\Delta E$ vary in a nonlinear way with temperature, light intensity and initiator concentration. The temperature field in the region exposed to the UV light is described by the heat conduction of Eq. (4), with the appropriate boundary conditions in terms of temperature, heat flux emitted from the laser and heat loss through convection [146]. The internal heat generated by the curing process is equal to $q_{\text{g}} = \rho \cdot h_{\text{P}} {\text{d}}\varrho / {\text{d}}t$ [146].

In order to describe the UV light intensity at a point, a Gaussian distribution over the resin surface, together with a decreasing function with depth according to Beer–Lambert’s law, is adopted. Then, the light intensity is written as

$$I\left( {s,z,t} \right) = I_{0} \exp \left[ { - 2\left( {\frac{s\left( t \right)}{{w_{\text{b}} }}} \right)^{2} } \right] \exp \left( { - e_{\beta } \left[ \beta \right]z} \right)$$

(21)

where $w_{\text{b}}$ is the laser beam radius and $s\left( t \right)$ represents the position in time of a generic point lying on the irradiated surface and $z$ represents the penetration depth (being $z = 0$ on the resin surface).

As highlighted from different FE analyses performed to assess the present model [145], the degree of cure $\varrho$ is affected by the AM process parameters, mainly light intensity, curing time and layer depth. Although this model provides an exhaustive description of the kinetic evolution—which is helpful to make some qualitative consideration on the mechanics of a printed component—a quantitative assessment of the relationship between the achieved degree of cure and the mechanical properties is lacking.

Pointwise mechanistic kinetic model

Anastasio et al. [142] proposed a pointwise mechanistic kinetic model, where the reaction scheme shown in Eq. (18) is described by the following set of differential equations

$$\begin{aligned} & \frac{{{\text{d}}\left[ \beta \right]}}{{{\text{d}}t}} = - k_{\text{d}} \left[ \beta \right] \\ & \frac{{{\text{d}}\left[ M \right]}}{{{\text{d}}t}} = - k_{\text{p}} \left[ M \right]\left[ {R^{ \cdot } } \right] - k_{\text{p}} \left[ M \right]\left[ {P^{ \cdot } } \right] \\ & \frac{{{\text{d}}\left[ {P_{\text{dead}} } \right]}}{{{\text{d}}t}} = k_{t} \left[ {P^{ \cdot } } \right]^{2} + k_{\text{t}} \left[ {P^{ \cdot } } \right]\left[ {R^{ \cdot } } \right] \\ & \frac{{{\text{d}}[R^{ \cdot } ]}}{{{\text{d}}t}} = 2\bar{f}k_{\text{d}} \left[ \beta \right] - k_{\text{p}} \left[ M \right]\left[ {R^{ \cdot } } \right] - k_{t} \left[ {P^{ \cdot } } \right]\left[ {R^{ \cdot } } \right] \\ & \frac{{{\text{d}}[P^{ \cdot } ]}}{{{\text{d}}t}} = k_{\text{p}} \left[ M \right]\left[ {R^{ \cdot } } \right] - k_{\text{t}} \left[ {P^{ \cdot } } \right]\left[ {R^{ \cdot } } \right] - 2 k_{\text{t}} \left[ {P^{ \cdot } } \right]^{2} \\ \end{aligned}$$

(22)

where square brackets indicate the concentration of the given variable.

Solving the previous differential equations requires the reaction rate constants $k_{\text{d}}$, $k_{\text{p}}$, $k_{\text{t}}$ and the initiator efficiency $\bar{f}$ to be determined. As it can be noticed, the degree of cure does not explicitly appear in the system, since it can only be evaluated once the problem related to the monomer conversion is solved, through the relationship $\varrho \left( t \right) = 1 - \frac{{\left[ {M\left( t \right)} \right]}}{{\left[ {M\left( {t = 0} \right)} \right]}}$, where $\left[ {M\left( t \right)} \right]$ is the concentration of the monomer molecules at the time $t$.

A key critical aspect of this model concerns the evaluation of the rate constants involved. The initiator decomposition rate $k_{\text{d}}$ is assessed through a modified Beer–Lambert’s law, since light intensity is the driving force of the free radicals’ activation. The propagation and termination rate constants $k_{\text{p}}$ and $k_{\text{t}}$ depend on the degree of cure, since diffusion-controlled effects can become a limiting factor due to the increasing viscosity of the medium [142]. Moreover, the initiator efficiency decreases with the degree of cure due to the recombination of free radicals [148, 149].

Figure 12 illustrates the influence of different process parameters on the kinetics of photopolymerisation, showing experimental data and model predictions. At a certain light intensity, one can note that the degree of cure is higher for higher concentrations of the initiator (Fig. 12a). On the other hand, increasing the light intensity for a fixed concentration has a positive effect on the degree of cure (Fig. 12b).

Figure 12

Adapted from [142]

Degree of cure as a function of curing time: a for different photo-initiators concentration, model fit and theoretical prediction for $\left[ \beta \right]$ = 0.3 wt%; b for different light intensities, model fit for an intensity $I_{0}$ = 8 mW/cm² and theoretical predictions for the other values.

The effect of the curing time $t_{\text{c}}$ on the mechanical behaviour of the printed component is shown in Fig. 13a, referred to samples obtained from the same process parameters and tested at room temperature ($T = 23\,^\circ {\text{C}})$. As expected, the material shows a rubber-like behaviour for shorter curing times, while it behaves like a glassy polymer when a higher degree of cure is attained. The corresponding values of the yield stress are plotted in Fig. 13b, as a function of the glass transition temperature measured through dynamic mechanical analysis (DMA). The rate and temperature dependence of the yield strength is usually modelled according to Eyring’s equation [129]

$$\sigma_{\rm y} \left( {\dot{\varepsilon },T} \right) = \frac{{k_{\text{B}} T}}{{V^{*} }}\sinh^{ - 1} \left[ {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}\exp \left( {\frac{\Delta E}{RT}} \right)} \right]$$

(23)

where $V^{*}$ is the activation volume and $\dot{\varepsilon }_{0}$ is the rate factor assumed by this model to be related to the light intensity, which can be determined from experimental fitting of the stress–strain curves at room temperature [142].

Figure 13

Adapted from [142]

a Stress–strain response of samples printed with different curing times. b Yield stress as a function of the measured glass temperature $T_{\text{g}}$ for each sample tested in a.

The results from experimental data and model fitting are illustrated in Fig. 14 for samples cured at different light intensities and maximum curing time $t_{\text{c}} = 200\,{\text{s}}$. At room temperature (Fig. 14a), the yield stress seems to be higher in samples cured with higher light intensities. On the other hand, Fig. 14b suggests an inverted trend when the same samples are tested under different temperatures but equally distant from the glass transition ($\Delta T_{\text{g}} = T - T_{\text{g}} = 66\,^\circ {\text{C}}$).

Figure 14

Adapted from [142]

aYield strength of maximum-cured samples with different light intensities, tested at the same room temperature and b tested at different room temperatures (fixed temperature difference from $T_{\text{g}}$).

The observed behaviour points at the influence of the glass transition temperature and its relationship with the kinetics of polymerisation. For shorter curing times, the material displays a lower glass transition temperature, which is then reflected in the rubber-like behaviour observed in Fig. 13 at room temperature. When the intensity of the UV light is increased, the glass transition temperature is increased as well, which explains the effect on the yield stress shown in Fig. 14a. The dependence of the glass transition temperature on the degree of cure is well known in the literature (e.g. [150, 151]), while direct relationships between $\varrho$ and the stress–strain curves of the material are more critical. The outcome obtained by Anastasio et al. [142] suggests that a unique correlation between the glass transition temperature and the mechanical behaviour cannot be found [142]. This is evident by looking at the results shown in Fig. 14b: according to models that link the mechanical response of a polymeric material to the temperature distance from $T_{\text{g}}$ [131], we should have obtained the same response for the two cases illustrated. Such a discrepancy might depend on the different microstructures of the materials cured at various light intensities (an in-depth discussion on this aspect can be found in “Discussion” section), pointing at the limitations of predicting the mechanical behaviour through approaches that neglect the role of the microstructure on the photopolymerisation process. In particular, the model cannot predict the different behaviour observed between glassy and rubber-like states, which is shown to occur depending on the adopted process parameters.

Spatial mechanistic kinetic model

Recently, Wu et al. [152] proposed a model, based on the mechanics of soft active materials with phase evolution [153], coupling the evolution of material properties during photopolymerisation with mechanical deformation. Similarly to the model reviewed in the previous section [142], it is based on rate equations to calculate the variation of the species concentrations; additionally, it includes the description of the spatial distribution of reactants inside the continuum body during the process. Therefore, the solution of the differential problem directly provides the evolution of the degree of cure $\varrho$ in space and time. Furthermore, the absorptivity described by the Beer–Lambert’s law is not simply that of the photo-initiators (as shown in [142]), but it is a combination of those of photo-initiator, resin and polymer, which evolve according to $\varrho$. This model has been used by the authors to assess the residual stress field, shrinkage evolution, etc., typically affecting photopolymerised components.

During polymerisation, cross-links are formed from the initial state of a viscous melt, leading to a denser polymer network and an increase in the material stiffness. According to the theory of phase evolution [153], when a material point is subjected to an external stimulus, such as the UV light, new phases are formed under stress-free conditions with specific volume fractions, at the expense of the phases already formed, thus leading to an unbalance in the mechanical equilibrium. Consequently, the newly formed cross-links do not carry any load, until the material deforms in order to restore the mechanical equilibrium. The rheological model proposed to describe this transformation consists of one spring of modulus $E_{\text{eq}}$ (representing all the equilibrium branches, i.e. the elastic response), and an arbitrary number $N_{\text{ne}}$ of non-equilibrium branches (Maxwell elements), each one characterised by a modulus $E_{\text{i}}$ and a relaxation time $\tau_{\text{i}}$ ($i = 1, \ldots ,N_{\text{ne}} )$, necessary to account for the nonlinear viscoelastic properties of the material. The equilibrium modulus $E_{\text{eq}} = 3\mu_{\text{eq}} = 3Nk_{\text{B}} T$ can be related to the achieved $\varrho$ by using the relationship:

$$E_{\text{eq}} = E_{\text{c}} \exp \left[ {b\left( { \varrho - \varrho_{\text{gel}} } \right)} \right] + E_{\text{d}}$$

(24)

where $E_{\text{c}} , E_{\text{d}}$ and $b$ are fitting parameters [154, 155], while $\varrho_{\text{gel}}$ is the degree of cure at the liquid–solid-state transition. The evolution of the number of cross-links during the photopolymerisation process can be derived according to $N = \frac{1}{{3k_{\text{B}} T}}\left\{ {E_{\text{c}} \exp \left[ {b\left( { \varrho - \varrho _{\text{gel}} } \right)} \right] + E_{\text{d}} } \right\}$, whose increase provides therefore an increase in the polymer network stiffness.

As for non-equilibrium branches, $E_{\text{i}}$ and $\tau_{\text{i}}$ have been estimated from experimental tests conducted on a fully cured sample and then predicted for other curing stages by means of the $\varrho$-temperature superposition [133]. Accordingly, the relaxation times for materials with different values of $\varrho$ are the results of the shifts in the relaxation times of the fully cured component, so that we can write

$$\tau_{\text{i}} \left( {\varrho ,T} \right) = A_{\text{P}} \left( {\varrho ,T} \right) \tau_{\text{i}} \left( {\varrho_{\text{ref}} ,T_{{{\text{g}},{\text{ref}}}} } \right)$$

(25)

being $\varrho_{\text{ref}} ,T_{{{\text{g}},{\text{ref}}}}$ quantities relative to the baseline values of density and glass transition temperature, respectively. The shift function $A_{\text{P}} \left( {\varrho ,T} \right)$ is related to the glass transition temperature of a material at a certain curing stage, which also depends on the degree of cure [156]. On the other hand, the moduli of non-equilibrium branches do not depend on the achieved value of $\varrho$ [152].

Finally, the stress state can be evaluated by adding the term in the equilibrium branch to that in non-equilibrium branches, $\varvec{\sigma}=\varvec{\sigma}_{\text{eq}} + \sum\nolimits_{i = 1}^{{N_{\text{ne}} }} {\varvec{\sigma}_{{{\text{neq}},i}} }$, where the Cauchy stress in the equilibrium branch can be obtained from a compressible neo-Hookean model, according to

$${\varvec{\upsigma}}_{\text{eq}} = J^{ - 1} (\mu_{\text{eq}} J^{{ - \frac{2}{3 }}} \left( {{\text{dev}} \varvec{B}} \right) + \kappa_{\text{eq}} \ln J \varvec{I})$$

(26)

where $J = { \det }\varvec{F}$ is the volume change ratio and $\varvec{B} = \varvec{FF}^{T}$ the left Cauchy–Green strain tensor. The shear and bulk moduli $\mu_{\text{eq}}$ and $\kappa_{\text{eq}}$ depend on the value of $\varrho$ achieved, as illustrated previously. Since we are interested in studying the mechanics of the component after printing, we can assume to leave the cured component in a stress-free state for some time before testing, so that the deformation gradient $\varvec{F}$ in Eq. (26) does not depend on the deformation history involved in the equilibrium branches during the process.

In order to evaluate $\varvec{\sigma}_{\text{neq,i}}$ as a function of the viscoelastic properties of the material, Wu et al. followed the approach proposed in [157,158,159]. By multiplicatively decomposing the total deformation gradient of each branch into an elastic part and a viscous one, i.e. $\varvec{F} = \varvec{F}_{i}^{\text{e}} \varvec{F}_{i}^{\text{v}}$, where $\varvec{F}_{i}^{\text{v}}$ is referred to the relaxed configuration obtained after elastically unloading from the deformation state given by $\varvec{F}_{i}^{\text{e}}$ (the subscript $i$ represents the ith branch), the Cauchy stress can be calculated as follows:¹

$$\varvec{\sigma}_{\text{neq,i}} = \frac{1}{{J_{i}^{\text{e}} }}\left[ {{\mathbb{C}}_{i}^{\text{e}} :\varvec{E}_{i}^{\text{e}} } \right]$$

(27)

where $J_{i}^{\text{e}} = \det \varvec{F}_{i}^{\text{e}}$, $\varvec{E}_{i}^{e}$ is the Hencky strain tensor and ${\mathbb{C}}_{i}^{e}$ is the fourth-order isotropic elastic tensor, defined as ${\mathbb{C}}_{i}^{e} = 2\mu_{i} \left( {{\mathbb{I}} - \frac{1}{3}\varvec{I} \otimes \varvec{I}} \right) + \kappa_{i} {\mathbf{\mathcal{I}}}$. Predictions provided by the model are compared with experimental results in Fig. 15.

Figure 15

Adapted from [152]

a Evolution of the degree of cure for different light intensities (red circles are experimental values for $I_{0} =$ 10 mW cm⁻²). b Stress–strain curves at equal light intensity, for different curing times. c Stress–strain curves of printed samples, at different light intensities (modelling results).

Phenomenological kinetic model

In a model recently proposed by Yang and Zhao [161], the degree of cure is put in relation with the mechanical properties of the printed components. The model analytically describes the curing of a component obtained by a photopolymerisation process, characterised by direct projection of an image layer with UV light, as shown in Fig. 16. A specific layer can be cured by the UV light more than once, as printed layers can still be slightly targeted by the light that penetrates through the new fresh layer. The model considers two types of production scenarios: in the first one (Fig. 16a), the liquid resin depth is greater than the part thickness in the building direction ($h_{\text{r}} \ge h$), while in the second scenario a portion of the printed part surmounts the liquid resin during the fabrication process (Fig. 16b). With respect to curing, the two scenarios imply an important difference. Since a printed layer is assumed to be re-cured when it is inside the photosensitive liquid resin, in the first case all printed layers are continuously cured during fabrication, while this is not the case for the second scenario. For the sake of brevity, we report herein only the analytical description of the model for the first case: the reader should refer to [161] for further details.

Figure 16

Adapted from [161]

Schematic view of the bottom-up SLA process and index notation for a scenario I and b scenario II. The light blue colour indicates the liquid monomer, while in dark blue the cured polymer is shown.

The degree of cure, for the specific ith layer when it is being cured for the jth time, is evaluated by means of the following phenomenological kinetic expression [162]

$$\varrho_{i}^{j} \left( {d,\theta } \right) = t_{ci}^{j} \left\{ {K_{P,0} I_{i}^{jp} \exp \left( { - \frac{\Delta E}{{RT_{i}^{j} \left( {d,\theta } \right)}}} \right)\left[ \beta \right]_{i}^{{j^{q} }} \varrho_{i}^{j} \left( {d,\theta } \right)^{m} \left[ {1 - \varrho_{i}^{j} \left( {d,\theta } \right)} \right]^{n} } \right\}$$

(28)

where $j = h /d - i + 1$, $K_{P,0}$ is the pre-exponential factor of the rate constant, the symbol $\theta$ identifies the stratification angle between surface normal vector and build direction, while $p,q,m,n$ are model parameters related to environmental condition, type of resin, etc., which are determined by best fitting of experimental results [161]. Notice that Eq. (28) has the same structure of Eq. (20), except from the fractional term related to the diffusion-controlled effects that are instead neglected in this model.

The photo-initiators concentration is assumed to decrease inversely with the degree of cure, being $\left[ \beta \right]_{i}^{j} = [\beta_{0} ]$ when $j = 1$ and $\left[ \beta \right]_{i}^{j} = \left[ \beta \right]_{i}^{j - 1} \left[ {1 - \varrho_{i}^{j - 1} \left( {d,\theta } \right)} \right]$ when $j \ge 2$. Finally, the degree of cure of the printed component is estimated by taking the average curing of the various layers

$$\varrho \left( {d,\theta } \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{h/d} \varrho_{i} \left( {d,\theta } \right)}}{h/d}$$

(29)

where the degree of cure of each layer is obtained from $\varrho_{i} \left( {d,\theta } \right) = \sum\nolimits_{j = 1}^{h/d - i + 1} {\varrho_{i}^{j} \left( {d,\theta } \right)}$.

It is worth noticing that Eq. (13) provides an overall value of the degree of cure for the entire printed component, instead that simply referred to a single layer as considered by other models.

Similarly to the approach proposed in [142], the model of Yang and Zhao [161] is capable of estimating the evolution of $\varrho$ by means of physical concepts, but the description of the mechanical behaviour of the printed component is still a matter of experimental fitting. An empirical expression of the ultimate tensile strength of the printed component, obtained through a fitting of stress–strain curves, has been proposed in the form $\sigma_{\rm U} = c_{1} \exp \left( {c_{2} \varrho } \right)$, where $c_{1} , c_{2}$ are fitting parameters [161].

Discussion

In the light of the above sections, it can be appreciated that laser-based additive manufacturing of polymeric materials involves complex chemical–physical phenomena that have relevant effects on the properties of the final part. Consequently, in order to predict the mechanical properties of the printed part, the additive process needs to be described through a proper representation of the main phenomena taking place during the fabrication, such as heat transfer, melting and merging of particles, densification, rheological aspects in SLS, and kinetics of polymerisation in SLA. While the description of the manufacturing process has been accomplished satisfactorily in most of the models reviewed in “Physical models of laser-based additive manufacturing of polymers” section, and the role of process parameters has been explored by extensive experimental work, we feel that an in-depth understanding of the relationship between printing process, fabrication parameters and mechanical characteristics after printing remains an open issue. In this final section of our review, we attempt to highlight the main mechanisms through which the mechanical properties of laser-based AM components are determined and how they are influenced by the process parameters.

The relationship existing between process parameters and final properties is often an indirect one; for instance, the ultimate tensile stress of a laser-sintered specimen depends on the energy density of printing through the effect that the latter has on the achieved density. As an example, the various aspects of SLS involved in the transformation from the raw material to the final part is illustrated in Fig. 17. In an attempt to establish quantitative connections between the various levels, optimisation algorithms and data-driven approaches seem to be a promising tool [163, 164]. In particular, multi-objective optimisation can be used to derive process–structure–property correlations and also to obtain inverse models, linking the desired performance with the fabrication parameters and the material’s characteristics. Such an approach combines an accurate analytical modelling of the AM process, including chemical–physical transformations in the microstructure, with extensive experimental validation [163].

Figure 17

Graphical representation of the relationships between raw material properties, process parameters, final parts and indicators of mechanical performances (elastic properties, fracture resistance, etc.) in selective laser sintering

The mechanical description of AM polymeric components through general models (such as those derived from Eyring’s rate-activated theory) has some limits in the possibility of accounting for different polymer structures at the mesoscale. This problem can be overcome if accurate, yet simple and easy-to-use physics-based models, are applied when designing the printing procedure and characterising the part. For instance, in the rate-based chemical reaction model of photopolymerisation [152], the mechanical behaviour of a component is directly related to the evolution of the cross-link density, which in turn is controlled by a combination of the main process parameters of SLA. In fact, depending on the achieved degree of cure and velocity of the reaction, a polymer can show a rubber-like behaviour (low values of $\varrho$) or a brittle one (high values of $\varrho$). On the other hand, irrespectively from the process conditions, the choice of a specific viscoelastic mechanical model, for the type of polymer being printed (thermoset or thermoplastic), also plays also a fundamental role. The simplest viscoelastic phenomenological approach is typically based on rheological models arranging in various assemblies two or more springs and dashpot elements [165]. Such an approach is often used for both thermosets and thermoplastics. The relaxation time of the dashpot branch is estimated according to the time-crystallisation-temperature-superposition (in thermoplastics), while it follows a time-degree of cure-temperature-superposition in thermosets. Other models aim at connecting the continuum-level viscoelasticity to the molecular-level mechanisms responsible for the viscoelastic behaviour. Among them, a successful approach describes the viscous response by harnessing the temperature-dependent bond kinetics existing at the molecular scale [166,167,168]. For instance, in polymers with physical bonds and in highly cross-linked thermosets (vitrimers) [169], the viscoelastic behaviour is modelled by means of the chains attachment and detachments mechanisms. In such polymers, viscoelastic effects (creep or stress relaxation) are triggered by temporary chains in the polymer network, which can detach from their stretched state and reattach to the network in a stress-free state upon dissociation and reformation of the dynamic cross-links [168]. The relationship between the attachment/detachment coefficients and the process parameters in SLA is still unknown and it is worth to be investigated, in order to use such models for modelling of thermosets in 3D printing.

The thermal process of laser sintering is the focus of most of the reviewed investigations dedicated to the SLS technology. Due to the superposition between the localised heat source, provided by laser exposure, and the heat transfer controlled by the processing temperature, phase transformations in the powder bed do not occur uniformly. Although traditional approaches based on a homogenised material provide good approximation of the heat transfer problem, there are specific aspects which require to directly account for the granular nature of the material. One of such cases is the process of laser energy absorption, where the effect of scattering in the semi-transparent polymeric powder might alter the energy density absorbed in depth [93]. However, what is the consequence of neglecting such a contribution on the prediction of the final properties of the material remains uncertain. With respect to the temperature evolution in the powder bed, a fundamental insight is provided by models that can account for multiple layers, as the local temperature is found to change during the printing process non-uniformly [95]. Coupled with accurate experimental works on the kinetics of crystallisation in semi-crystalline polymers, we might have the tools to highlight the limits of the largely adopted assumption of a quasi-isothermal processing window. Beyond a certain number of layers, which is usually exceeded in the production of the final component, the transition from a mostly viscous liquid to a viscoelastic solid is initiated well before the beginning of the controlled cooling stage [46]. The effect of the crystalline phase of laser-sintered parts has been related to the temperature- and rate-dependent behaviour of polymeric materials [127], and the effect of inhomogeneous crystallisation was also linked to warping of the printed parts [91]. In general, the behaviour of semi-crystalline polymers is complex because of different contributions during the deformation of the material, deeply affected by rate and temperature [176]. When subjected to tensile loading, initially the process is governed by rupture and reorientation in the crystalline regions, while the latter stage of deformation is linked to the amorphous region [177]. The limited number of investigations dedicated to the role of crystallisation in SLS, together with the growing number of semi-crystalline polymers that are becoming available for sintering, suggests that further work is needed in this area.

A large number of works have explored the influence of process parameters on the mechanical behaviour of laser-sintered parts adopting an experimental approach. The sensitivity to various parameters of Young’s modulus, ultimate tensile stress and elongation at break for polyamide 12 components is illustrated qualitatively in Fig. 18a [54]. While this information might be useful for optimal planning of SLS, it is appropriate to understand the physical origin behind the observed variations.

Figure 18

a Sensitivities of mechanical properties to the process parameters (from uniaxial tension tests on PA12 specimens). Adapted from [54]. b Variation of the elongation at break with part density (from uniaxial tension tests at constant speed, equal to 5 mm min⁻¹, on PA12 specimens printed with different energy densities [48, 52, 59]

In this work, we have stressed the primary importance covered by bond formation and powder densification, which surprisingly is neglected in some of the reviewed contributions or included through a simplified empirical form. Binding mechanisms have indeed a strong effect on the behaviour of the final part: since the process of bond formation is controlled by temperature changes and capillary forces without applying external pressure, pores are inevitably formed, due to imperfect binding between the powder particles, unmolten inclusions, shrinkage or trapped gas. As such, porosity is unavoidably present in laser-sintered components and it is seen as the main responsible for inferior mechanical performances with respect to traditional manufacturing methods [124]. Although the energy density of the process, as defined in “Selective laser sintering” section, is a good predictor with respect to part density, more subtle phenomena have been observed [50, 52]. In particular, properties such as the elastic modulus or the yield strength appear to be less critical with respect to ultimate properties, such as the elongation at break. Indeed, testing of polyamide laser-sintered parts showed that they comply to standard injection moulded samples in terms of Young’s modulus, but their elongation at break is approximately one order of magnitude lower, suggesting a more brittle behaviour. In other terms, the presence of defects seems to have a large effect on elongation and a relatively smaller influence on yield strength and Young’s modulus of the material [50]. The variation of Young’s modulus and elongation at break with the part density of laser-sintered samples is plotted in Fig. 18b (from specimens of polyamide 12 material processed at different energy densities).

Rather than focusing on simply predicting the mechanical strength of a piece, models should be developed to provide a detailed description of the deformation in the porous structure, as these mechanisms are more critical and probably less investigated. In this sense, the role of the laser energy on melting and bond formation is delicate: low energy densities are responsible for incomplete binding, whereas at higher energy a reduced ductility is due to a decrease in the average molecular weight due to thermal degradation [52]. In addition to intralayer porosity, interlayer adhesion is particularly relevant in terms of fracture, as the existence of coplanar voids might lead to crack propagation in these regions. With respect to the fracture mechanisms observed in tensile specimens stretched perpendicularly to the building direction, depending on the energy density a transition from delamination to brittle fracture and finally ductile fracture is observed [50]. These aspects should be carefully considered when modelling the ultimate behaviour of the printed components: suggested approaches based on void growth, such as the GTN’s model adopted in [134, 135], are suitable for ductile damage only. Mechanically, the building direction plays the role of introducing a certain degree of anisotropy in the material [178, 179]; differently from others traditional simpler additive manufacturing techniques (such as the FDM, [30]) in which the induced anisotropy has been deeply studied and quantified, in SLS and SLA the degree of anisotropy of the printed material has not been univocally recognised and quantified. As a matter of fact, in SLS the resulting material has been experimentally found to show a transversely isotropic elasticity and failure strain, while it is generally orthotropic concerning the ultimate tensile strength [180]. Several authors state that build orientation slightly affects the mechanical properties of SLA components, so that components should be considered isotropic [74, 75]. For instance, Hague et al. [74] have found low variations (around 5–10%) of the elastic modulus and tensile strength for different building orientations, so that they concluded that the build orientation has little effects on the mechanical properties of the components.

An additional insight in the actual chemical–physical process involved in SLA is provided by theoretical models, based, for instance, on the kinetic theory of photopolymerisation [76]. As it is shown in “Photopolymerisation” section, these models allow the identification of the most critical process parameters involved in SLA (e.g. light intensity, curing time, cure depth, etc.) and determine how these can be related.

In “Photopolymerisation” section, we present the main available models used to describe the properties of an AM material produced by photopolymerisation, although several other studies related to SLA and the assessment of the amount of cure have been published [170,171,172,173,174,175]. Overall, it emerges that the main process parameters involved in a kinetic description of photopolymerisation, and in turn those most relevant for the final mechanics of a component, are light intensity and curing time. In addition, kinetic models are able to capture the effect of other printing parameters, such as layer thickness and post-curing time. For instance, it is shown that low values of the layer thickness ensure an improved mechanical performance. In a photopolymerised component, this fact is strictly related to the kinetics of the process: for an assigned light intensity and curing time, a higher and more uniform degree of cure within the whole layer is allowed if printing with a lower thickness. On the contrary, higher layer thicknesses produce a good degree of cure only in the region that is irradiated by the laser directly, possibly requiring an increased curing time and/or light intensity to ensure a complete and uniform cure of the layer. In this context, a FE implementation of the kinetic model (see, for instance, [145]) can help to tune light intensity, curing time and layer thickness in order to achieve the required degree of cure within the whole layer. Since the final component is printed layer by layer, a high and uniform average cure level is expected to provide an enhanced strength. A schematic view of this concept is represented for a single-layer component in Fig. 19, where the evolution of the average degree of cure is plotted for two different layer thicknesses (Fig. 19a). The qualitative results in terms of stress–strain response are shown in Fig. 19b, under the assumption of equal curing time $t_{\text{c}}$.

Figure 19

Schematic view of the effects of different layer thicknesses on the evolution of the degree of cure (a) and on the mechanics of the two components after the same curing time $t_{\text{c}}$ (b). All other parameters, such as peak light intensity $I_{0}$ and photo-initiator concentration, are kept fixed

However, an AM component is made of several layers. From FE simulations, we are able to predict the degree of cure point by point, and consequently layer by layer, so that an overall degree of cure of the entire component can be estimated by using some averaging operation (see, for instance, Eq. 29, “Phenomenological kinetic model” section). An alternative to cumbersome numerical simulations of the whole AM process consists in analysing a single layer by using, for instance, a simple kinetic model as explained above; in order to predict the average value of the degree of cure of the entire printed part, the outcomes of the single-layer analysis can be extended to the component made of many layers through a homogenisation approach.

Aiming at further improving the mechanical performance of a component, post-curing treatments might be applied to complete the polymerisation process after printing. As shown in [142], kinetic models are able to describe the role of post-curing time $t_{\text{pc}}$ in improving the degree of cure, depending on the curing achieved during printing. This aspect is shown schematically in Fig. 20, where two components, showing different degrees of cure after printing, are compared qualitatively. Specifically, after the same curing time $t_{\text{c}}$, the component denoted with $A_{1}$ that was exposed to a greater light intensity $I_{\text{A}}$ as already completed curing ($\varrho \to 1$), whereas component $B_{1}$ (with $I_{\text{B}} \ll I_{\text{A}}$) has not. During the subsequent post-curing treatment, there is no further change on the degree of cure of $A_{1}$, see ($A_{1} + A_{2} )$ in Fig. 20a, and this is also reflected in the uniaxial stress–strain curve sketched in Fig. 20b. On the contrary, the post-curing time has a positive effect on the degree of cure of component $B_{1}$, see ($B_{1} + B_{2} )$ in Fig. 20a, and on the mechanical response of the component shown in Fig. 20b. For the sake of simplicity, the increase in the degree of cure in the post-curing treatment has been assumed linear with respect to the post-curing time (red dashed line in Fig. 20a); the real trend can be inferred by means of a kinetic model governed by the parameters involved in the post-curing stage. (Notice that the light intensity can be different from that adopted during the printing process.)

Figure 20

Schematic view of the effect of post-curing on the degree of cure a and on the mechanical behaviour of a component, before and after post-curing time b

The velocity of the photopolymerisation reaction should not be neglected either. As highlighted in [142], faster curing promoted by a high light intensity produces shorter and more cross-linked polymer chains, because of premature initiation in different points and faster termination of reactions (see a schematic view of this concept in Fig. 21). This could imply that the knowledge of the achieved degree of cure alone is not enough to correctly predict the mechanical behaviour of the AM component. Mechanical models describing the polymer network according to physically based mesoscale parameters may be helpful [181]. Accordingly, to achieve the same degree of cure, high curing rates (i.e. by supplying high light intensity in a short time) result in short polymer chains with a low number of Kuhn segments $N_{\rm s,A}$ per chain, while low curing rates result in longer chains with a larger number of Kuhn’s segments $N_{\rm s,B}$ (Fig. 21). It is known that different chain lengths lead to a substantial difference in the limit stretch (whose value is typically defined to be $\lambda_{\hbox{max} } = \sqrt {N_{\text{S}} }$) of a component and in the ultimate stress (whose amount depends on the monomer atoms bonding energy, [182]), since both aspects depend on the so-called mean square length of the chain end-to-end vector $r_{0} = b\sqrt {N_{\text{S}} }$ in the undeformed configuration (being $b$ the Kuhn’s segment length, see [181] for more details). With respect to this point, the mechanical model presented in [152] does not take into account the length of a single chain in terms of Kuhn’s segments, since it evaluates the degree of cure which is related only to the evolution of the number of chains per unit volume, irrespectively of their length. Future research should investigate the relationship existing between the degree of cure and the time required to reach such a value, as this might have an implication on the polymer network at the mesoscale and consequently on the mechanical performances of the component.

Figure 21

Effects of the velocity of photopolymerisation on the polymer networks at the mesoscale

Concluding remarks

In this paper, we have presented an extensive review on processes and mechanical models related to laser-based additive manufacturing of polymeric materials, broadly differentiated between laser sintering and photopolymerisation technologies. Besides briefly discussing the peculiar characteristics of each of these technologies, the main goal of the review has been to provide a comprehensive description of the physical parameters influencing the mechanical behaviour of AM components, and how they are determined by the manufacturing process. The fundamental physical–mechanical models proposed in the literature to simulate the additive manufacturing process have been critically reviewed, with the attempt of offering to the reader an overall view of the limitations of current modelling and suggest possible improvements.

In SLS, the granular nature of the polymeric powder has non-negligible influence on the mechanisms of energy absorption, phase transformations and sintering, and as such, we believe that multi-scale models are a promising approach for simulating the whole manufacturing process of the material. Laser scan spacing and velocity along with layer thickness are regarded as the key process parameters controlling the mechanical performances of the AM component, e.g. in terms of elongation at break, tensile strength and elastic modulus. Moreover, a direct correlation between apparent density of the AM component and its elongation at break has been clearly observed.

In photopolymerisation, available literature models, based on either pointwise or spatial approaches, describe the photo-thermal kinetic process of the chemical transformation from monomers in liquid state to polymeric chains. The degree of cure is the key parameter governing the mechanical response of the AM component, including tensile strength and brittle/ductile behaviour, where such a degree is affected by curing and post-curing time as well as by layer thickness and material absorbance.

In conclusion, we strongly believe that the increasingly demand for printing reliable AM components offering—beyond the usual request of geometric precision and dimensional stability—the required levels of performance and safety (including load bearing capacity, structural integrity, durability, geometric distortion tolerance, etc.), as well as customisation for the ever-expanding applications of additive manufacturing sector, requires a multi-faceted approach. The understanding of the complete process–structure–property relationship is a fundamental step which is required not only to improve the current accuracy, efficiency and sustainability of the additive manufacturing techniques, but also for future material development. In particular, if an additive manufactured object is expected to precisely fulfil some quantitative prescription on its mechanical properties, we should be able to predict the mechanical features of the printed component through the understanding and modelling of the influence that process parameters have on the chemical–physical AM transformation, by means of powerful, reliable and easy-to-use physics-based models.