Background

There is a growing interest in the potential of paper as a flexible substrate for functional coatings, particularly of nanomaterials, and printed electronics. Recent examples include flexible chemiresistor sensors from coatings of carbon nanotubes [1] and graphene [2], flexible silver nanowire circuits, e.g. foldable RFID antennae [3], and optoelectronic devices from graphene on paper [4].

Several recent studies identify the surface roughness of paper as an important parameter in its performance as a substrate for functional coatings. Morais et al. [5] investigated the use of papers with different roughnesses as substrates for organic electronic devices and observed a strong dependence of sheet resistance on surface roughness. Similarly, Zikulnig et al. [6] observed an order of magnitude difference in the resistance of printed silver nanoparticle sensors on paper substrates, which was attributed to differences in surface roughness and sheet porosity. Further, Liu et al. [7] noted the influence of roughness not only on the global electrical performance of carbon nanotube thin-film transistors on paper, but on its local uniformity also. It is noteworthy also that the surface roughness of paper-like materials influences the performance of other material systems: for fuel cells employing carbon fibre nonwovens in the gas diffusion layer, roughness affects contact resistance with the polymer electrolyte membrane [8], and in electrospun polymer scaffolds for tissue engineering, it affects wettability [9].

Figure 1
figure 1

Example surface profile showing datum \(d = 0\) at the highest point in the profile and mean plane of profile \(\bar{d}\) as computed from measurements \(d_i\)

Full size image

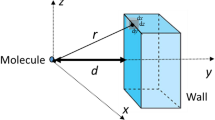
As might be anticipated given the long-standing and still ubiquitous use of printed paper, there is a substantial literature relating surface topography of paper to print quality, see, for example, [10,11,12,13,14]. Indeed, the first industrial application of scanning electron microscopy was the analysis of the surface of papers [15, 16] to understand its influence on printability. Perhaps, the earliest quantitative analysis of paper topography is provided by Hsu [17, 18], who reported lognormal, i.e. positively skewed, distributions of ‘depression depth’, confirming that the distribution is asymmetrical about the mean; similarly, the more recent and detailed analysis of Mettänen [19] reports a positive skew for the surface ‘height’ distribution. As for general classes of rough surfaces, the full range of standard roughness parameters [20] have been applied to the study of paper roughness, see, for example, Vernhes et al. [21], who noted the scale dependence of roughness measures and correlation lengths. In what follows, we will focus our analyses on the arithmetic mean roughness average, \(R_{\mathrm{a}}\), and the root-mean-square roughness, \(R_{\mathrm{q}}\). We define these with reference to Fig. 1, which shows a stochastic rough surface. In a given profile the distance, d is measured in a discrete process from a datum located at the highest point, yielding n uniformly spaced measurements of \(d_i\). The roughnesses \(R_{\mathrm{a}}\) and \(R_{\mathrm{q}}\) are given by

$$\begin{aligned} R_{\mathrm{a}}&= \frac{1}{n}\,\sum _{i=1}^{n} \left| d_i - \bar{d}\right| \end{aligned}$$
(1)
$$\begin{aligned} R_{\mathrm{q}}&= \sqrt{\frac{1}{n}\,\sum _{i=1}^{n} (d_i - \bar{d})^2}\ \ , \end{aligned}$$
(2)

respectively, where \(\bar{d}\) is the mean depth of the profile. We note that \(R_{\mathrm{q}}\) is the standard deviation of d.

Despite there being a rich body of literature providing models for the structure of stochastic fibrous materials such as paper and nonwoven textiles [22, 23], there are few theoretical treatments giving their roughness in terms of fibre and network properties. Dodson shows that the distribution of ‘surface pore heights’ for a random fibre network, i.e. one where fibres are deposited independently of each other according to a point Poisson process in two dimensions, is well described by an exponential distribution [24] with mean proportional to the fibre thickness, t. We note that the exponential distribution has standard deviation equal to the mean, so this dependency on fibre thickness will persist also in \(R_{\mathrm{a}}\) and \(R_{\mathrm{q}}\). Niskanen et al. [25] used Poisson statistics to estimate \(R_{\mathrm{q}}\) for a random fibre network as

$$\begin{aligned} R_{\mathrm{q}} = \bar{z} \sqrt{\frac{m_{\mathrm{f}}}{A\,\bar{\beta }}}\ , \end{aligned}$$
(3)

where \(\bar{z}\) and \(\bar{\beta }\) are the mean thickness and mean mass per unit area of the network, respectively, A is the area of a measuring head, such as a stylus or laser spot, and \(m_{\mathrm{f}}\) is the mass of a fibre. The dependence of \(R_{\mathrm{q}}\) on fibre mass predicted by Eq. (3) is in agreement with Dodson’s prediction of the effect of fibre thickness, since thicker fibres will be heavier than thinner ones of the same length; it is confirmed also by the experimental results of Li and Green [26]. However, the dependence of \(R_{\mathrm{q}}\) on network thickness and areal density provided by Eq. (3) is at variance with our intuitive understanding of roughness as a surface property. In part, the dependence can be attributed to network apparent density, \(\rho _{\mathrm{a}}\), which is given by the ratio \(\bar{\beta }/\bar{z}\) [27], such that

$$\begin{aligned} R_{\mathrm{q}} = \sqrt{\frac{\bar{z}\,m_{\mathrm{f}}}{A\,\rho _{\mathrm{a}}}}\ . \end{aligned}$$
(4)

Although the roughness of paper is well known to exhibit an inverse dependence on density, as predicted by Eq. (4), the residual dependence on thickness is manifestly incorrect. The independence of roughness and thickness is supported by Li and Green [26] who concluded that the roughness of a fibre mat is determined by the surface 10 \(\mathrm {g}\,\mathrm{m}^{-2}\) only. Further, Bennis and Benslimane [28] showed that \(R_{\mathrm{a}}\) correlated with the porosity of surface layers, which is manifestly not a thickness-dependent property.

Here we derive expressions for the relationship between \(R_{\mathrm{a}}\) and \(R_{\mathrm{q}}\) for random fibre networks and provide theory giving these in terms of fibre dimensions and sheet properties. We compare our results with data from the literature and with those arising from experiments using papers with a range of densities formed in the laboratory using different fibres.

Theory

Consider the distance, d, from a datum located at the highest point in a given sample to the rough surface of a fibre network, as shown in Fig. 1. From our earlier discussion, we expect the distribution of d to exhibit a positive skew. A good candidate distribution for, d, is the gamma distribution, which has been widely applied to the modelling of pore size in a broad family of materials [29, 30], including stochastic fibrous materials [31,32,33]. The gamma distribution has probability density

$$\begin{aligned} f(d) = \left( \frac{k}{\bar{d}}\right) ^k\,\frac{d^{k-1}\,\mathrm{e}^{-k\,d/\bar{d}}}{\Gamma (k)}\ , \end{aligned}$$
(5)

where \(\Gamma (k)\) is the Gamma function; the distribution has mean \(\bar{d}\) and variance \(\sigma ^2(d) = \bar{d}^2/k\). The gamma distribution includes the exponential distribution, as used in Dodson’s theory [24], as a special case when \(k = 1\) and describes the intervals between independent random, i.e. Poissonian, events. Accordingly, Eq. (5) gives the probability density of d for random structures when \(k = 1\) and that of ‘near random’ structures, with variance dependent on parameter \(k > 0\) [34].

From Eq. (1), it follows that

$$\begin{aligned} R_{\mathrm{a}}&= \int _{0}^{\bar{d}} (\bar{d}-d)\,f(d)\,\mathrm {d}d + \int _{\bar{d}}^{\infty } (\bar{d}-d)\,f(d)\,\mathrm {d}d \nonumber \\&= 2\,\bar{d}\,\,\frac{k^{k}\,\mathrm{e}^{-k}}{\Gamma (k+1)}\ . \end{aligned}$$
(6)

We denote the random case when \(k = 1\) by an asterisk:

$$\begin{aligned} R^*_{\mathrm{a}} =\frac{2}{e}\,\bar{d} \ . \end{aligned}$$
(7)

From Eq. (2), we have

$$\begin{aligned} R_{\mathrm{q}} = \sigma (d) = \frac{\bar{d}}{\sqrt{k}} \ , \end{aligned}$$
(8)

such that, from Eq. (6), we obtain

$$\begin{aligned} R_{\mathrm{q}} = \frac{\mathrm{e}^k\,k^{k- \frac{1}{2}}\,\Gamma (k)}{2}\,R_{\mathrm{a}} \ , \end{aligned}$$
(9)

and

$$\begin{aligned} R^*_{\mathrm{q}}= \frac{e}{2}\,R^*_{\mathrm{a}} \ . \end{aligned}$$
(10)

The ratio \(R_{\mathrm{q}}/R_{\mathrm{a}}\) as given by Eq. (9) is plotted in Fig. 2, where the broken horizontal line represents \(\lim _{k \rightarrow \infty } R_{\mathrm{q}}/R_{\mathrm{a}} = \sqrt{\pi /2} \approx 1.25\). We observe very rapid convergence on this asymptotic value. The in-plane structure of paper is known to exhibit greater variability than a random network formed from the same constituent fibres due to flocculation in the forming process [23]; in contrast, we expect processes such as pressing and drying against smooth plates to remove small asperities from fibre surfaces giving a slightly lower variability in the measured distance d and hence reduced roughness. As such, the range of application for our equations is \(k \ge 1\).

Figure 2
figure 2

Ratio \(R_{\mathrm{q}}/R_{\mathrm{a}}\) as given by Eq. (9) plotted against parameter k. The ratio rapidly converges on an asymptote at \(R_{\mathrm{q}}/R_{\mathrm{a}} = \sqrt{\pi /2}\)

Full size image

We seek now an expression for \(\bar{d}\) in terms of fibre and network variables. It is straightforward to show [22, 35] that the mean plane perpendicular dimension of voids within a network with porosity \(\varepsilon \) formed from fibres with thickness t is

$$\begin{aligned} \bar{h} = \frac{\varepsilon }{1 - \varepsilon }\,t \ . \end{aligned}$$
(11)

Now, whereas internal voids are bounded by the surfaces of vertically adjacent fibres, those in the surface are bounded by a fibre on one side only. Accordingly, we expect to a first approximation that

$$\begin{aligned} \bar{d} = \frac{\bar{h}}{4} = \frac{\varepsilon _{\mathrm{s}}}{1 - \varepsilon _{\mathrm{s}}}\,\frac{t}{4} \ , \end{aligned}$$
(12)

where the subscript s is introduced such that \(\varepsilon _{\mathrm{s}}\) is the surface porosity. Tomographic analysis of paper reveals a through-thickness distribution of porosity, with surface layers being more porous than those in the bulk of the sheet [36], as anticipated for a rough near planar porous material. Subsequent tomographic analysis [27] has shown recently that for paper with bulk porosity, \(\varepsilon _\mathrm{b}\), the mean surface porosity is approximated by

$$\begin{aligned} \varepsilon _{\mathrm{s}} = \frac{1 + \varepsilon _\mathrm{b}}{2}\ \ . \end{aligned}$$
(13)

Further, for papers with areal density greater than about 40 \(\mathrm {g}\,\mathrm{m}^{-2}\), the bulk region dominates such that \(\varepsilon \approx \varepsilon _\mathrm{b}\) [27] and substitution of Eq. (13) in Eq. (12) yields on manipulation

$$\begin{aligned} \bar{d} = \frac{t}{4}\,\frac{1+ \varepsilon }{1-\varepsilon }\ \ . \end{aligned}$$
(14)

Substitution of Eq. (14) in Eq. (6) yields

$$\begin{aligned} R_{\mathrm{a}}&= \frac{t}{2}\,\frac{1+ \varepsilon }{1-\varepsilon }\,\frac{k^k\,\mathrm{e}^{-k}}{\Gamma (k+1)} \end{aligned}$$
(15)
$$\begin{aligned} R^*_{\mathrm{a}}&= \frac{t}{2\mathrm{e}}\,\frac{1+ \varepsilon }{1-\varepsilon } \end{aligned}$$
(16)
$$\begin{aligned} R_{\mathrm{q}}&= \frac{t}{4}\,\frac{1+ \varepsilon }{1-\varepsilon }\,\frac{1}{\sqrt{k}} \end{aligned}$$
(17)
$$\begin{aligned} R^*_{\mathrm{q}}&= \frac{t}{4}\,\frac{1+ \varepsilon }{1-\varepsilon } \end{aligned}$$
(18)

We proceed to compare the predictions of Eqs. (9) and (15) to (18) with surface roughness data obtained from the literature and with experiments carried out using paper samples with systematically varying properties.

Experiment

Experiments were carried out to form paper samples in the laboratory according to international standards (TAPPI T-205 sp-02) and to measure their surface roughness. To test the dependence on fibre thickness, t, wood pulps with different morphologies were selected for papermaking: two hardwoods, birch (Södra Gold), eucalyptus (Portucel), and two softwoods, spruce (Mercer International) and pine (Stora Enso, Lapponia). All pulps were commercially produced by the Kraft process and bleached. To test the predicted dependency of roughness on sheet porosity, pulps were beaten in a Valley beater (TAPPI T-200 sp-01). Beaten pulps were sampled at 30-min intervals and 60 \(\mathrm {g}\,\mathrm{m}^{-2}\) handsheets made according to standard (TAPPI T-205 sp-02); note that the standard specifies that sheets are in contact with a polished steel plate on one side during the pressing and drying phases of manufacture, resulting in this side being smoother than the other.

Fibre dimensions were measured for each condition sampled using a Metso FS5 fibre analyser (Metso, Espoo, Finland); as anticipated, the width \(\omega \) and linear density \(\delta \) of fibres were very insensitive to beating and fibre length decreased. Given that we expect no significant influence of fibre length on the roughness parameters \(R_{\mathrm{a}}\) and \(R_{\mathrm{q}}\), we report fibre data for the unbeaten conditions only in Table 1, where data are reported as averages of measurements on over 10000 fibres. Following Kallmes and Bernier [37], collapsed fibre thickness was calculated using

$$\begin{aligned} t = \frac{\delta }{\omega \,\rho }\ , \end{aligned}$$
(19)

where \(\rho \) is the density of cellulose and was assumed to be 1.55 \(\mathrm{g}\,\mathrm{cm}^{-3}\). As a rule of thumb, we expect the thickness of a fibre to be about double that of its cell wall.

Table 1 Fibre dimensions for unbeaten fibres
Full size table

Samples were conditioned for at least 24 h at 23 ± 1 \(^\circ \)C and 50 ± 2% RH. Areal density, \(\bar{\beta }\), and thickness, \(\bar{z}\) (TAPPI T-220 sp-01 & TAPPI T-411 om-97, respectively), were measured, allowing calculation of their apparent density, \(\rho _{\mathrm{a}}\), and their porosity, \(\varepsilon = 1 - \rho _{\mathrm{a}}/\rho \); for recent discussion of these measures and their interdependencies, see [27]. Surface roughness was measured on both sides of the handsheets using a DektakXT diamond stylus profilometer (Bruker, Tucson, Arizona) fitted with a 2.5-\(\upmu \mathrm {m}\) stylus with a 3 mg tracking force over a 2-mm scan line; we note this is comparable to the fibre lengths reported in Table 1 and observe from the subsequently reported results that this length is more than 2 orders of magnitude greater than our measures of roughness. Five repeats were carried out for each condition.

Figure 3
figure 3

Scanning electron micrographs of rough surfaces or sheets. Extent of beating, and hence density, increases from left to right, and effect on surface texture is immediately evident with fine fibrillar material infilling inter-fibre voids at higher densities. Scale bar applies to all images

Full size image

Results and discussion

Scanning electron micrographs of the rough sides of handsheets with a range of densities are shown in Fig. 3. The porosities of the samples, as calculated from their areal density, thickness, and the density of cellulose, decreased from around 0.7–0.4. The change in density and hence in the roughness of the surface is evident on first inspection; it is clear also that infilling of inter-fibre voids with fine, fibrillar material contributes strongly to the changes in surface structure due to beating. From theory for the in-plane dimensions of pores in fibre networks [33], we can estimate the change in surface pore size associated with the observed reduction in density as being around 80%. The difference between rough and smooth sides of the sheet is illustrated in Fig. 4 using higher magnification images of both sides of a pine handsheet and of a eucalyptus handsheet, both made from pulps beaten for 30 min. We observe that the uppermost fibre surfaces are very smooth where these have been pressed and dried in contact with the polished steel plate; these flat fibre surfaces are absent from the rough side of the sheets. This phenomenon was reported by Emerton et al. [38], who observed similar effects in the surface fibres of commercial machine-glazed papers. As such, we expect a smaller contribution of the small-scale fibre roughness to the sheet roughness on the plate-dried side than on the rough side.

Figure 4
figure 4

Scanning electron micrographs of rough side and plate side of handsheets made from pine pulp beaten for 30 min (top row) and eucalyptus pulp beaten for 30 min (bottom row); arrows show surface fibres that have been smoothed by contact with the polished plate. Scale bar applies to all images

Full size image

Figure 5 shows \(R_{\mathrm{q}}\) plotted against \(R_{\mathrm{a}}\) as measured on both sides of the sheet. The broken lines represent the relationships \(R_{\mathrm{q}} = \sqrt{\pi /2}\,R_{\mathrm{a}} \approx 1.25\,R_{\mathrm{a}}\) and \(R^*_{\mathrm{q}} = \mathrm{e}\,R^*_{\mathrm{a}}/2 \approx 1.36\,R_{\mathrm{a}}\) as given by Eqs. (9) and (10), respectively. The predicted linear dependence is immediately evident, and data are tightly bound by the lower range of the expected envelope; linear regression on the data yields \(R_{\mathrm{q}} = 1.25\,R_{\mathrm{a}}\) with coefficient of determination \(r^2 = 0.998\). The inset figure shows the data of Barros and Johansson [12] obtained from commercially manufactured papers; these exhibit the same dependence, also with gradient 1.25. Importantly, these commercial paper samples will exhibit structural anisotropy in the form of a fibre orientation distribution and will have greater in-plane variability than laboratory papers [23]. Further, whereas our data were obtained using stylus profilometry, those of Barras and Johansson arise from 2D optical system, strongly indicating that the linear dependence of \(R_{\mathrm{q}}\) on \(R_{\mathrm{a}}\) is not an artefact of the measurement system. For completeness, we note also that the data of Zikulnig et al. [6] obtained using white light interferometry on two commercial papers give the ratio of \(R_{\mathrm{q}}\)–\(R_{\mathrm{a}}\) as approximately 1.35.

Figure 5
figure 5

\(R_{\mathrm{q}}\) plotted against \(R_{\mathrm{a}}\) for handsheets. Broken lines represent the expected range of dependence of \(R_{\mathrm{q}}\) on \(R_{\mathrm{a}}\) as given by Eqs. (9) and (10). Inset plot shows the data of Barras and Johansson [12]

Full size image

Figure 6 shows \(R_{\mathrm{q}}\) plotted against \(R_{\mathrm{a}}\) for the data of El-kharouf et al. [8] obtained using interferometry of nonwoven carbon fibre networks used in gas diffusion layers in fuel cells. The higher roughness observed for these materials is consistent with their higher porosity as reported by El-kharouf et al. [8]; although they do not report fibre diameters, our experience of such materials suggests that they would be of order 10 \(\upmu \mathrm {m}\), so greater than the collapsed thickness of wood pulp fibres, such that these would contribute to greater roughness also. The samples investigated by El-kharouf et al. [8] included those with a range of coatings and treatments; nonetheless, all data in Fig. 6 fall within the expected envelope. Given the very high degree of correlation between \(R_{\mathrm{q}}\) and \(R_{\mathrm{a}}\) observed for our data and those from the literature, we consider only \(R_{\mathrm{q}}\) in our subsequent discussion.

Figure 6
figure 6

\(R_{\mathrm{q}}\) plotted against \(R_{\mathrm{a}}\) carbon fibre networks used as gas diffusion layers in fuel cells from the data of El-kharouf et al. [8]. Broken lines represent the expected range of dependence of \(R_{\mathrm{q}}\) on \(R_{\mathrm{a}}\) as given by Eqs. (9) and (10)

Full size image

From Eqs. (17) and (18), we expect a plot of \(R_{\mathrm{q}}/t\) against \((1 + \varepsilon )/(1-\varepsilon )\) to be linear with gradient 1/4 in the random case and with a smaller gradient, \(1/(4\,\sqrt{k})\) otherwise. This is plotted for our data in Fig. 7 where the broken lines represent linear regressions on the data with coefficients of determination \(r^2 = 0.867\) for the rough side and \(r^2 = 0.738\) for the plate side. For the rough side of our samples, we obtain a gradient of 0.27, which is close to the predicted value for the random case; for the plate side of our samples, we obtain a gradient of 0.135, which corresponds to that predicted when \(k \approx 3.4\) such that Eq. (9) yields \(R_{\mathrm{q}} \approx 1.28\,R_{\mathrm{a}}\), providing a useful check. We note that in the random case (\(k =1\)), the exponential distribution is a monotonically decreasing function of d, whereas for \(k > 1\), the gamma distribution exhibits a maximum at \((k-1)\,\bar{d}/k\). Accordingly, we can interpret the higher value of k obtained for the smooth side of our samples as a reduced contribution of fibre roughness to that of the sheet, such that the probability of small d is less for the smooth side than for the rough, resulting in a maximum in the distribution of d. For completeness, we note that the intercept of relevance is that when \(\varepsilon = 0\) such that \((1 + \varepsilon )/(1-\varepsilon ) = 1\). Given our assumptions and approximate method for determining porosity, it is perhaps unsurprising that this is nonzero. Nonetheless, it is encouraging that this offset is similar for both sides of our samples.

Figure 7
figure 7

\(R_{\mathrm{q}}/t\) plotted against \((1 + \varepsilon )/(1-\varepsilon )\) for our handsheet samples. Broken lines represent linear regressions on the data

Full size image

Conclusions

We have presented a statistical model for the roughness of random and near random heterogeneous fibrous materials. Our theory uses the gamma distribution to represent the distribution of heights of a surface profile and predicts that the relationship between the standard roughness metrics \(R_{\mathrm{a}}\) and \(R_{\mathrm{q}}\) is approximately linear and bound within a narrow envelope. Comparison with data from our experiments on paper samples with a range of densities formed from different fibre types confirms this prediction, as do data from the literature for commercially produced papers and for carbon fibre nonwovens for fuel cells. Further, we have provided equations, showing that the absolute values of \(R_{\mathrm{a}}\) and \(R_{\mathrm{q}}\) are proportional to the thickness of constituent fibres and dependent on a simple function of network porosity. Agreement with data from our experimental paper samples is very good.