Skip to main content
SpringerLink
Log in

Modeling of mass flow behavior of hot rolled low alloy steel based on combined Johnson-Cook and Zerilli-Armstrong model

  • Original Paper
  • Published:
Journal of Materials Science Aims and scope Submit manuscript

Abstract

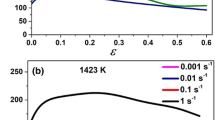
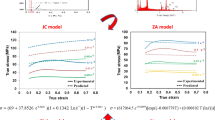
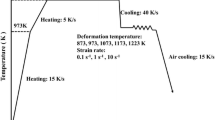
Accuracy and reliability of numerical simulation of hot rolling processes are dependent on a suitable material model, which describes metal flow behavior. In the present study, Gleeble hot compression tests were carried out at high temperatures up to 1300 °C and varying strain rates for a medium carbon micro-alloyed steel. Based on experimental results, a Johnson-Cook model (JC) and a Zerilli-Armstrong (ZA) model were developed and exhibited limitation in characterizing complex viscoplastic behavior. A combined JC and ZA model was introduced and calibrated through investigation of strain hardening, and the coupled effect of temperature and strain rate. Results showed that the combined JC and ZA model demonstrated better agreement with experimental data. An explicit subroutine of the proposed material model was coded and implemented into a finite element model simulating the industrial hot rolling. The simulated rolling torque was in good agreement with experimental data. Plastic strain and stress distributions were recorded to investigate nonlinear mass flow behavior of the steel bar. Results showed that the maximum equivalent plastic strain occurred at 45° and 135° areas of the cross section. Stress increased with decreasing temperature, and the corresponding rolling torque was also increased. Due to the extent of plastic deformation, rolling speed had limited influence on the internal stress of the bar, but the relative rolling torque was increased due to strain rate hardening.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8
Figure 9
Figure 10
Figure 11
Figure 12
Figure 13
Figure 14
Figure 15
Figure 16
Figure 17
Figure 18
Figure 19

Similar content being viewed by others

References

  1. G. R. Johnson, W. H. Cook (1983) “A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures,” 7th International Symposium on Ballistics 21: 541–547

  2. Zhang H, Wen W, Cui H (2009) Behaviors of IC10 alloy over a wide range of strain rates and temperatures: experiments and modeling. Mater Sci Eng A 504(1–2):99–103

    Article  Google Scholar 

  3. Lin Y, Chen X, Liu G (2010) A modified Johnson-Cook model for tensile behaviors of typical high-strength alloy steel. Mater Sci Eng A 527(26):6980–6986

    Article  Google Scholar 

  4. Gambirasio L, Rizzi E (2016) An enhanced Johnson-Cook strength model for splitting strain rate and temperature effects on lower yield stress and plastic flow. Comput Mater Sci 113:231–265

    Article  Google Scholar 

  5. Lin Y, Chen X (2011) A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater Des 32:1733–1759

    Article  Google Scholar 

  6. Zerilli FJ, Armstrong RW (1987) Dislocation-mechanics-based constitutive relations for material dynamics calculations. J Appl Phys 61(5):1816–1825

    Article  Google Scholar 

  7. Samantaray D, Mandal S, Bhaduri AK (2009) A comparative study on Johnson Cook, modified Zerilli-Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr–1Mo steel. Comput Mater Sci 47(2):568–576

    Article  Google Scholar 

  8. Samantaray D, Mandal S, Borah U, Bhaduri AK, Sivaprasad PV (2009) A thermo-viscoplastic constitutive model to predict elevated-temperature flow behaviour in a titanium-modified austenitic stainless steel. Mater Sci Eng A 526(1–2):1–6

    Article  Google Scholar 

  9. Lin YC, Chen XM (2010) A combined Johnson-Cook and Zerilli-Armstrong model for hot compressed typical high-strength alloy steel. Comput Mater Sci 49(3):628–633

    Article  Google Scholar 

  10. Shida S (1969) Empirical formula of flow stress of carbon steels—resistance to deformation of carbon steels at elevated temperature. J Jpn Soc Technol Plast 10:610–617

    Google Scholar 

  11. Kim S, Im Y (2002) Three-dimensional finite element analysis of non-isothermal shape rolling. J Mater Process Technol 127:57–63

    Article  Google Scholar 

  12. Duan X, Sheppard T (2002) Three dimensional thermal mechanical coupled simulation during hot rolling of aluminium alloy 3003. Int J Mech Sci 44:2155–2172

    Article  Google Scholar 

  13. Yang H, Wang M, Guo L, Sun Z (2008) 3D coupled thermo-mechanical FE modeling of blank size effects on the uniformity of strain and temperature distributions during hot rolling of titanium alloy large rings. Comput Mater Sci 44(2):611–621

    Article  Google Scholar 

  14. S. Rummel, D. Van Aken, R. O’Malley, X. Wang, K. Chandrashekhara (2015) High strain rate hot deformation of steels: measurement and simulation. In: Proceedings of the International Conference on Advances in Product Metallurgy of Long and Forged Products, pp 1–10, Vail.

  15. Nalawade RS, Puranik AJ, Balachandran G, Mahadik KN, Balasubramanian V (2013) Simulation of hot rolling deformation at intermediate passes and its industrial validity. Int J Mech Sci 77:8–16

    Article  Google Scholar 

  16. Benasciutti D, Brusa E, Bazzaro G (2010) Finite elements prediction of thermal stresses in work roll of hot rolling mills. Procedia Eng 2:707–716

    Article  Google Scholar 

  17. Li K, Wang P, Liu G, Yuan P, Zhang Q (2016) Development of simulation system for large H-beam hot rolling based on ABAQUS. Int J Adv Manuf Technol 85(5):1649–1663

    Article  Google Scholar 

  18. Hosseini Kordkheili SA, Ashrafian MM, Toozandehjani H (2014) A rate-dependent constitutive equation for 5052 aluminum diaphragms. Mater Des 60:13–20

    Article  Google Scholar 

  19. C. Y. Gao, “FE realization of thermo-visco-plastic constitutive models using VUMAT in ABAQUS/Explicit Program” (2007). Comput Mech ISCM2007, pp 623–628

  20. He A, Xie G, Zhang H, Wang X (2013) A comparative study on Johnson-Cook, modified Johnson-Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel. Mater Des 52:677–685

    Article  Google Scholar 

  21. Dusunceli N, Colak OU, Filiz C (2010) Determination of material parameters of a viscoplastic model by genetic algorithm. Mater Des 31(3):1250–1255

    Article  Google Scholar 

  22. Awais M, Lee HW, Im YT, Kwon HC, Byon SM, Park HD (1984) Plastic work approach for surface defect prediction in the hot bar rolling process. J Mater Process Technol 201(73–78):2008.

    Google Scholar 

Download references

Acknowledgements

This work was supported by the Peaslee Steel Manufacturing Research Center at Missouri University of Science and Technology. The authors would like to thank Geary W. Ridenour from Gerdau—Fort Smith for technical input, and also Rafael Pizarro Sanz from Gerdau—Spain for Gleeble testing.

Author information

Authors and Affiliations

  1. Department of Mechanical and Aerospace Engineering, Missouri University of Science and Technology, Rolla, MO, 65409, USA

    X. Wang & K. Chandrashekhara

  2. Department of Materials Science and Engineering, Missouri University of Science and Technology, Rolla, MO, 65409, USA

    S. A. Rummel, S. Lekakh, D. C. Van Aken & R. J. O’Malley

Authors
  1. X. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. Chandrashekhara
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. A. Rummel
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. S. Lekakh
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. D. C. Van Aken
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. R. J. O’Malley
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to K. Chandrashekhara.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, X., Chandrashekhara, K., Rummel, S.A. et al. Modeling of mass flow behavior of hot rolled low alloy steel based on combined Johnson-Cook and Zerilli-Armstrong model. J Mater Sci 52, 2800–2815 (2017). https://doi.org/10.1007/s10853-016-0570-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10853-016-0570-8

Keywords

Search

Navigation