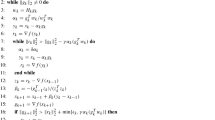Abstract
In this paper we derive a unified framework for the taut-string algorithm and regularization with G-norm data fit. The G-norm data fit criterion (popularized in image processing by Y. Meyer) has been paid considerable interest in regularization models for pattern recognition. The first numerical work based on G-norm data fit has been proposed by Osher and Vese. The taut-string algorithm has been developed in statistics (Mammen and van de Geer and Davies and Kovac) for denoising of one dimensional sample data of a discontinuous function. Recently Hinterberger et al. proposed an extension of the taut-string algorithm to higher dimensional data by introducing the concept of tube methods. Here we highlight common features between regularization programs with a G-norm data fit term and taut-string algorithms (respectively tube methods). This links the areas of statistics, regularization theory, and image processing.
Similar content being viewed by others
References
R.A. Adams, Sobolev Spaces, Academic Press: New York, 1975.
J.-F. Aujol, G. Aubert, L. Blanc-Féraud, and A. Chambolle, “Image decomposition application to SAR images,” in [6], 2003, pp. 297–312.
P.L. Davies and A. Kovac, “Local extremes, runs, strings and multiresolution,” Ann. Statist., 29:1–65, 2001. With discussion and rejoinder by the authors.
L.C. Evans and R.F. Gariepy, Measure Theory and Fine Properties of Functions, CRC–Press: Boca Raton, 1992.
D. Gilbarg and N.S. Trudinger, Elliptic Partial Differential Equations of Second Order. Classics in Mathematics, Springer-Verlag: Berlin, 2001. Reprint of the 1998 edition.
L.D. Griffin M. Lillholm (Eds.)Scale-Space Methods in Computer Vision. Lecture Notes in Computer Science Vol. 2695, Springer Verlag, 2003. Proceedings of the 4th International Conference, Scale-Space 2003, Isle of Skye, UK, June 2003.
P. Grisvard, Elliptic Problems in Nonsmooth Domains, Pitman: Boston, 1985.
W. Hinterberger, M. Hintermüller, K. Kunisch, M. von Oehsen, and O. Scherzer,“Tube methods for BV regularization,” JMIV, Vol. 19, pp. 223–238, 2003.
E. Mammen and S. van de Geer, “Locally adaptive regression splines,” Ann. Statist., Vol. 25, pp. 387–413, 1997.
Y. Meyer, Oscillating patterns in image processing and nonlinear evolution equations, volume 22 of University Lecture Series, American Mathematical Society: Providence, RI, 2001.
S. Osher, L.I. Rudin, “Feature-oriented image enhancement using shock filters,” SIAM J. Numer. Anal., Vol. 27, No. 4, pp. 919–940, 1990.
S. Osher, A. Solé, and L. Vese, “Image decomposition and restoration using total variation minimization and the H −1-norm,” Multiscale Model. Simul., Vol. 1, No. 3, pp. 349–370, 2003.
St. Osher and R. Fedkiw, Level Set Methods and Dynamic Implicit Surfaces, volume 153 ofApplied Mathematical Sciences, Springer-Verlag: New York, 2003.
St. Osher and N. Paragios, Geometric Level Set Methods in Imaging, Vision, and Graphics, Springer-Verlag: New York, 2003.
L.I. Rudin, S. Osher, and E. Fatemi, “Nonlinear total variation based noise removal algorithms,” Physica D, Vol. 60, pp. 259–268, 1992.
R. Temam, Problèmes mathématiques en plasticité, volume 12 of Méthodes Mathématiques de l’Informatique [Mathematical Methods of Information Science]. Gauthier-Villars: Montrouge, 1983.
L. Vese and S. Osher, “Modelling textures with total variation minimization and oscillating pattern in image processing,” SIAM, J. Sci. Comput., 2003 (to appear).
E. Zeidler, Nonlinear Functional Analysis and its Applications I, Springer-Verlag: New York, 1993. corrected printing.
Author information
Authors and Affiliations
Corresponding author
Additional information
Otmar Scherzer received his Ph.D. in Mathematics from the University of Linz, Austria, in 1990. Till 1999 he has been at the Industrial Mathematics Institute at the University of Linz. From 1999–2000 he visited the University of Munich (Germany) and from 2000–2001 he was Professor at the University of Bayreuth (Germany). Since 2001 he is Professor at the Department of Computer Science at the University of Innsbruck (Austria). From 1995 to 1996 he had an Erwin Schrödinger Scholarship of the Austrian Science Foundation (FWF) for visiting Texas A&M University and the University of Delaware (USA). Otmar Scherzer received the Award of the Austrian Mathematical Society (1998) and the START-price of the FWF in (1999). He is in the editorial board of Numerical Functional Analysis and Optimization and Inverse Problems. His research interest include image processing and inverse problems.
Rights and permissions
About this article
Cite this article
Scherzer, O. Taut-String Algorithm and Regularization Programs with G-Norm Data Fit. J Math Imaging Vis 23, 135–143 (2005). https://doi.org/10.1007/s10851-005-6462-1
Issue Date:
DOI: https://doi.org/10.1007/s10851-005-6462-1