Abstract
Modal accounts of normality in non-monotonic reasoning traditionally have an underlying semantics based on a notion of preference amongst worlds. In this paper, we motivate and investigate an alternative semantics, based on ordered accessibility relations in Kripke frames. The underlying intuition is that some world tuples may be seen as more normal, while others may be seen as more exceptional. We show that this delivers an elegant and intuitive semantic construction, which gives a new perspective on defeasible necessity. Technically, the revisited logic does not change the expressive power of our previously defined preferential modalities. This conclusion follows from an analysis of both semantic constructions via a generalisation of bisimulations to the preferential case. Reasoners based on the previous semantics therefore also suffice for reasoning over the new semantics. We complete the picture by investigating different notions of defeasible conditionals in modal logic that can also be captured within our framework.










Similar content being viewed by others
References
Alchourrón, C., Gärdenfors, P., & Makinson, D. (1985). On the logic of theory change: Partial meet contraction and revision functions. Journal of Symbolic Logic, 50, 510–530.
Askounis, D., Koutras, C., & Zikos, Y. (2012). Knowledge means ‘all’, belief means ‘most’. In L. Fariñas del Cerro, A. Herzig, & J. Mengin (Eds.), Proceedings of the 13th European conference on logics in artificial intelligence (JELIA), no. 7519 in LNCS (pp. 41–53). Berlin: Springer.
Baltag, A., & Smets, S. (2006). Dynamic belief revision over multi-agent plausibility models. In W. van der Hoek & M. Wooldridge (Eds.), Proceedings of LOFT (pp. 11–24). Liverpool: University of Liverpool.
Baltag, A., & Smets, S. (2008). A qualitative theory of dynamic interactive belief revision. In G. Bonanno, W. van der Hoek, & M. Wooldridge (Eds.), Logic and the foundations of game and decision theory (LOFT7), no. 3 in texts in logic and games (pp. 13–60). Amsterdam: Amsterdam University Press.
Benferhat, S., Dubois, D., & Prade, H. (1999). Possibilistic and standard probabilistic semantics of conditional knowledge bases. Journal of Logic and Computation, 9(6), 873–895.
Blackburn, P., Benthem, J., & Wolter, F. (2006). Handbook of Modal Logic. Amsterdam: Elsevier North-Holland.
Booth, R., Casini, G., Meyer, T., & Varzinczak, I. (2015). On the entailment problem for a logic of typicality. In Proceedings of the 24th international joint conference on artificial intelligence (IJCAI).
Booth, R., Meyer, T., & Varzinczak, I. (2012). PTL: A propositional typicality logic. In L. Fariñas del Cerro, A. Herzig, & J. Mengin (Eds.), Proceedings of the 13th European Conference on Logics in Artificial Intelligence (JELIA), no. 7519 in LNCS (pp. 107–119). Berlin: Springer.
Booth, R., Meyer, T., & Varzinczak, I. (2013). A propositional typicality logic for extending rational consequence. In E. Fermé, D. Gabbay, & G. Simari (Eds.), Trends in belief revision and argumentation dynamics, studies in logic—Logic and cognitive systems (Vol. 48, pp. 123–154). London: King’s College Publications.
Boutilier, C. (1994). Conditional logics of normality: A modal approach. Artificial Intelligence, 68(1), 87–154.
Britz, K., Casini, G., Meyer, T., & Varzinczak, I. (2013). Preferential role restrictions. In Proceedings of the 26th international workshop on description logics (pp. 93–106).
Britz, K., Heidema, J., & Meyer, T. (2008). Semantic preferential subsumption. Proceedings of the 11th international conference on principles of knowledge representation and reasoning (KR) (pp. 476–484). Cambridge: AAAI Press/MIT Press.
Britz, K., Meyer, T., & Varzinczak, I. (2011). Preferential reasoning for modal logics. Electronic Notes in Theoretical Computer Science, 278, 55–69. Proceedings of the 7th Workshop on Methods for Modalities (M4M’2011).
Britz, K., Meyer, T., & Varzinczak, I. (2011). Semantic foundation for preferential description logics. In D. Wang & M. Reynolds (Eds.), Proceedings of the 24th Australasian Joint Conference on Artificial Intelligence, no. 7106 in LNAI (pp. 491–500). Berlin: Springer.
Britz, K., Meyer, T., & Varzinczak, I. (2012). Normal modal preferential consequence. Proceedings of the 25th Australasian joint conference on artificial intelligence (pp. 505–516). Berlin: Springer.
Britz, K., & Varzinczak, I. (2013). Defeasible modalities. In Proceedings of the 14th Conference on Theoretical Aspects of Rationality and Knowledge (TARK) (pp. 49–60).
Britz, K., & Varzinczak, I. (2016a). Introducing role defeasibility in description logics. In L. Michael & A. Kakas (Eds.), Proceedings of the 15th European conference on logics in artificial intelligence (JELIA), no. 10021 in LNCS (pp. 174–189). Berlin: Springer.
Britz, K., & Varzinczak, I. (2016b). Preferential modalities revisited. In Proceedings of the 16th International Workshop on Nonmonotonic Reasoning (NMR).
Britz, K., & Varzinczak, I. (2017a). Context-based defeasible subsumption for \(d{{mathcal SROIQ}}\). In Proceedings of the 13th international symposium on logical formalizations of commonsense reasoning.
Britz, K., & Varzinczak, I. (2017b). Towards defeasible \(d{\cal{SROIQ}}\). In Proceedings of the 30th international workshop on description logics (Vol. 1879). CEUR Workshop Proceedings.
Britz, K., & Varzinczak, I. (2017c) From KLM-style conditionals to defeasible modalities, and back. Journal of Applied Non-Classical Logics. https://doi.org/10.1080/11663081.2017.1397325
Casini, G., Meyer, T., Moodley, K., Sattler, U., & Varzinczak, I. (2015). Introducing defeasibility into OWL ontologies. In M. Arenas, O. Corcho, E. Simperl, M. Strohmaier, M. d’Aquin, K. Srinivas, P. Groth, M. Dumontier, J. Heflin, K. Thirunarayan, & S. Staab (Eds.), Proceedings of the 14th international semantic web conference (ISWC), no. 9367 in LNCS (pp. 409–426). Berlin: Springer.
Casini, G., & Straccia, U. (2010). Rational closure for defeasible description logics. In T. Janhunen & I. Niemelä (Eds.), Proceedings of the 12th European conference on logics in artificial intelligence (JELIA), no. 6341 in LNCS (pp. 77–90). Berlin: Springer.
Crocco, G., & Lamarre, P. (1992). On the connections between nonmonotonic inference systems and conditional logics. In R. Nebel, C. Rich, & W. Swartout (Eds.), Proceedings of the 3rd international conference on principles of knowledge representation and reasoning (KR) (pp. 565–571). Burlington: Morgan Kaufmann Publishers.
Dubois, D., Lang, J., & Prade, H. (1994). Possibilistic logic. In D. Gabbay, C. Hogger, & J. Robinson (Eds.), Handbook of logic in artificial intelligence and logic programming (Vol. 3, pp. 439–513). Oxford: Oxford University Press.
Friedman, N., & Halpern, J. (2001). Plausibility measures and default reasoning. Journal of the ACM, 48(4), 648–685.
Gärdenfors, P., & Makinson, D. (1994). Nonmonotonic inference based on expectations. Artificial Intelligence, 65(2), 197–245.
Giordano, L., Gliozzi, V., Olivetti, N., & Pozzato, G. (2007). Preferential description logics. Logic for programming, artificial intelligence, and reasoning (LPAR), no. 4790 in LNAI (pp. 257–272). Berlin: Springer.
Giordano, L., Gliozzi, V., Olivetti, N., & Pozzato, G. (2013). A non-monotonic description logic for reasoning about typicality. Artificial Intelligence, 195, 165–202.
Giordano, L., Gliozzi, V., Olivetti, N., & Pozzato, G. (2015). Semantic characterization of rational closure: From propositional logic to description logics. Artificial Intelligence, 226, 1–33.
Hansson, B. (1969). An analysis of some deontic logics. Noûs, 3, 373–398.
Hansson, S. (1999). A textbook of belief dynamics: Theory change and database updating. Dordrecht: Kluwer.
Hawthorne, J. (2007). Nonmonotonic conditionals that behave like conditional probabilities above a threshold. Journal of Applied Logic, 5(4), 625–637.
Hodges, W. (1993). Model Theory. Cambridge: Cambridge University Press.
Katsuno, H., & Mendelzon, A. (1991). Propositional knowledge base revision and minimal change. Artificial Intelligence, 3(52), 263–294.
Kraus, S., Lehmann, D., & Magidor, M. (1990). Nonmonotonic reasoning, preferential models and cumulative logics. Artificial Intelligence, 44, 167–207.
Lehmann, D. (1995). Another perspective on default reasoning. Annals of Mathematics and Artificial Intelligence, 15(1), 61–82.
Lehmann, D., & Magidor, M. (1992). What does a conditional knowledge base entail? Artificial Intelligence, 55, 1–60.
Lewis, D. (1973). Counterfactuals. Oxford: Blackwell.
Lewis, D. (1974). Semantic analyses for dyadic deontic logic. Logical theory and semantic analysis (pp. 1–14). Dordrecht: D. Reidel Publishing Company.
Liau, C. J. (1999). On the possibility theory-based semantics for logics of preference. International Journal of Approximate Reasoning, 20(2), 173–190.
Liau, C. J., & Lin, B. P. (1996). Possibilistic reasoning-a mini-survey and uniform semantics. Artificial Intelligence, 88(1–2), 163–193.
Lindström, P. (1966). First-order predicate logic with generalized quantifiers. Theoria, 32, 186–195.
Makinson, D. (1993). Five faces of minimality. Studia Logica, 52, 339–379.
Makinson, D. (2005). Bridges from classical to nonmonotonic logic, texts in computing (Vol. 5). London: King’s College Publications.
Shoham, Y. (1988). Reasoning about change: Time and causation from the standpoint of artificial intelligence. Cambridge: MIT Press.
Stalnaker, R. (1968). A theory of conditionals. In N. Rescher (Ed.), Studies in logical theory (pp. 98–112). Oxford: Blackwell.
Veloso, P., Veloso, S., Viana, J., de Freitas, R., Benevides, M., & Delgado, C. (2009). On vague notions and modalities: A modular approach. Logic Journal of the IGPL, 18(3), 381–402.
Acknowledgements
We would like to thank the anonymous referees for their constructive comments and suggestions. This work was partially funded by the National Research Foundation of South Africa (UIDs 81225 and 85482, IFR1202160021 and IFR2011032700018).
Author information
Authors and Affiliations
Corresponding author
Additional information
A preliminary version of the work reported in this paper was presented at the Workshop on Nonmonotonic Reasoning (Britz and Varzinczak 2016b).
Proof of Theorem 1
Proof of Theorem 1
In the following,  we denote the dual of
we denote the dual of  in the usual sense, i.e.,
in the usual sense, i.e.,  .
.
Definition 14
(Subsentence) Let  . The set of subsentences of \(\alpha \), denoted by \({\text { sub}(\alpha )}\), is defined inductively by:
. The set of subsentences of \(\alpha \), denoted by \({\text { sub}(\alpha )}\), is defined inductively by:
-
If \(\alpha =\top \) or \(\alpha =\bot \), then \({\text { sub}(\alpha )}\mathrel {\mathop :}=\{\alpha \}\);
-
If \(\alpha =p\in \mathcal {P}\), then \({\text { sub}(\alpha )}\mathrel {\mathop :}=\{p\}\);
-
If \(\alpha =\beta \wedge \gamma \) or \(\alpha =\beta \vee \gamma \) or \(\alpha =\beta \rightarrow \gamma \), then \({\text { sub}(\alpha )}\mathrel {\mathop :}=\{\alpha \}\cup {\text { sub}(\beta )}\cup {\text { sub}(\gamma )}\);
-
If \(\alpha =\lnot \beta \) or \(\alpha =\Diamond _{i}\beta \) or \(\alpha =\Box _{i}\beta \) or
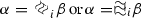 , then \({\text { sub}(\alpha )}\mathrel {\mathop :}=\{\alpha \}\cup {\text { sub}(\beta )}\).
, then \({\text { sub}(\alpha )}\mathrel {\mathop :}=\{\alpha \}\cup {\text { sub}(\beta )}\).
Definition 15
(Closure under subsentences) Let  . We say \(\mathcal {C}\) is closed under its subsentences if and only if \(\bigcup \{{\text { sub}(\alpha )} \mid \alpha \in \mathcal {C}\}\subseteq \mathcal {C}\).
. We say \(\mathcal {C}\) is closed under its subsentences if and only if \(\bigcup \{{\text { sub}(\alpha )} \mid \alpha \in \mathcal {C}\}\subseteq \mathcal {C}\).
Definition 16
(\(\mathcal {C}\)-type) Let  and let \(\mathscr {R}=\langle { W},{ R},{ V},\ll \rangle \) be an \({ R}\)-ordered model. For every \(w\in { W}\),
and let \(\mathscr {R}=\langle { W},{ R},{ V},\ll \rangle \) be an \({ R}\)-ordered model. For every \(w\in { W}\),
is the \(\mathcal {C}\)-type of w in \(\mathscr {R}\).
Definition 17
(\(\mathcal {C}\)-equivalence) Let  be finite and let \(\mathscr {R}=\langle { W},{ R},{ V},\ll \rangle \) be an \({ R}\)-ordered model. For every \(w,w'\in { W}\), \(w\simeq _{\mathcal {C}}w'\) if and only if \(t_{\mathcal {C}}(w)=t_{\mathcal {C}}(w')\). (It is easy to see that \(\simeq _{\mathcal {C}}\) is an equivalence relation on \({ W}\).) With \([w]_{\mathcal {C}}\mathrel {\mathop :}=\{w' \mid w\simeq _{\mathcal {C}}w'\}\), we denote the \(\mathcal {C}\)-equivalence class of \(w\in { W}\).
be finite and let \(\mathscr {R}=\langle { W},{ R},{ V},\ll \rangle \) be an \({ R}\)-ordered model. For every \(w,w'\in { W}\), \(w\simeq _{\mathcal {C}}w'\) if and only if \(t_{\mathcal {C}}(w)=t_{\mathcal {C}}(w')\). (It is easy to see that \(\simeq _{\mathcal {C}}\) is an equivalence relation on \({ W}\).) With \([w]_{\mathcal {C}}\mathrel {\mathop :}=\{w' \mid w\simeq _{\mathcal {C}}w'\}\), we denote the \(\mathcal {C}\)-equivalence class of \(w\in { W}\).
Definition 18
(\(\mathcal {C}\)-filtration) Let  be finite and let \(\mathscr {R}=\langle { W},{ R},{ V},\ll \rangle \) be an \({ R}\)-ordered model. Moreover, let:
be finite and let \(\mathscr {R}=\langle { W},{ R},{ V},\ll \rangle \) be an \({ R}\)-ordered model. Moreover, let:
-
\({ W}'\mathrel {\mathop :}={ W}/\simeq _{\mathcal {C}}\) (i.e., \({ W}'=\{[w]_{\mathcal {C}} \mid w\in { W}\}\));
-
\({ R}'\mathrel {\mathop :}=\langle { R}'_{1},\ldots ,{ R}'_{n} \rangle \), where \({ R}'_{i}\mathrel {\mathop :}=\{([w]_{\mathcal {C}},[w']_{\mathcal {C}}) \mid (w,w')\in { R}_{i}\}\), \(i=1,\ldots ,n\);
-
\({ V}':{ W}'\longrightarrow \{0,1\}^{\mathcal {P}}\), with \({ V}'([w]_{\mathcal {C}})={ V}(w)\);
-
\(\ll '=\langle \ll '_{1},\ldots ,\ll '_{n} \rangle \), where \(\ll '_{i}\mathrel {\mathop :}=\{([w]_{\mathcal {C}}[v]_{\mathcal {C}},[w']_{\mathcal {C}}[v']_{\mathcal {C}}) \mid (wv,w'v')\in \ll _{i}\) and either \(w\notin [w']_{\mathcal {C}}\) or \(v\notin [v']_{\mathcal {C}}\}\), \(i=1,\ldots ,n\). (It is not hard to check that each \(\ll '_{i}\) is a strict well-founded partial order).
With \(\mathscr {R}'\mathrel {\mathop :}=\langle { W}',{ R}',{ V}',\ll ' \rangle \) we denote the \(\mathcal {C}\)-filtration of \(\mathscr {R}\).
In Definition 18, the purpose of the clause “either \(w\notin [w']_{\mathcal {C}}\) or \(v\notin [v']_{\mathcal {C}}\)” is to prevent two indistinguishable (w.r.t. \(\mathcal {C}\)) pairs of worlds from inducing a reflexive \(\ll '_{i}\)-edge, which would violate the stated condition that \(\ll '_{i}\) must be a strict partial order.
Lemma 5
(Minimality preservation) Let  be finite and closed under subsentences, let \(\mathscr {R}=\langle { W},{ R},{ V},\ll \rangle \) be an \({ R}\)-ordered model, and let \(\mathscr {R}'=\langle { W}',{ R}',{ V}',\ll ' \rangle \) be the \(\mathcal {C}\)-filtration of \(\mathscr {R}\). Then, for \(i=1,\ldots ,n\), (i) if \((w,v)\in \min _{\ll _{i}}{ R}_{i}\), then \(([w]_{\mathcal {C}},[v]_{\mathcal {C}})\in \min _{\ll '_{i}}{ R}'_{i}\), and (ii) if \(([w]_{\mathcal {C}},[v]_{\mathcal {C}})\in \min _{\ll '_{i}}{ R}'_{i}\), then there are \(w'\in [w]_{\mathcal {C}}\) and \(v'\in [v]_{\mathcal {C}}\) such that \((w',v')\in \min _{\ll _{i}}{ R}_{i}\).
be finite and closed under subsentences, let \(\mathscr {R}=\langle { W},{ R},{ V},\ll \rangle \) be an \({ R}\)-ordered model, and let \(\mathscr {R}'=\langle { W}',{ R}',{ V}',\ll ' \rangle \) be the \(\mathcal {C}\)-filtration of \(\mathscr {R}\). Then, for \(i=1,\ldots ,n\), (i) if \((w,v)\in \min _{\ll _{i}}{ R}_{i}\), then \(([w]_{\mathcal {C}},[v]_{\mathcal {C}})\in \min _{\ll '_{i}}{ R}'_{i}\), and (ii) if \(([w]_{\mathcal {C}},[v]_{\mathcal {C}})\in \min _{\ll '_{i}}{ R}'_{i}\), then there are \(w'\in [w]_{\mathcal {C}}\) and \(v'\in [v]_{\mathcal {C}}\) such that \((w',v')\in \min _{\ll _{i}}{ R}_{i}\).
Proof
Showing (i): Assume \(([w]_{\mathcal {C}},[v]_{\mathcal {C}})\notin \min _{\ll '_{i}}{ R}'_{i}\). If \(([w]_{\mathcal {C}},[v]_{\mathcal {C}})\notin { R}'_{i}\), then \((w,v)\notin { R}_{i}\) and we are done. If there is \(([w']_{\mathcal {C}},[v']_{\mathcal {C}})\in { R}'_{i}\) such that \(([w']_{\mathcal {C}},[v']_{\mathcal {C}})\ll '_{i}([w]_{\mathcal {C}},[v]_{\mathcal {C}})\), then, by the construction of \(\ll '_{i}\), we have \((x,y)\ll _{i}(w,v)\) for some \(x\in [w]_{\mathcal {C}}\) and \(y\in [v]_{\mathcal {C}}\). Hence \((w,v)\notin \min _{\ll _{i}}{ R}_{i}\).
Showing (ii): Let \(X\mathrel {\mathop :}=\{(w',v') \mid w'\in [w]_{\mathcal {C}}\) and \(v'\in [v]_{\mathcal {C}}\}\). Assume \(X\cap \min _{\ll _{i}}{ R}_{i}=\emptyset \). Then for every \((w',v')\in X\) there must be \((x,y)\in { R}_{i}\) such that \((x,y)\ll _{i}(w',v')\). Moreover, \(x\notin [w]_{\mathcal {C}}\) or \(y\notin [v]_{\mathcal {C}}\), otherwise \((x,y)\in X\). Hence \(([x]_{\mathcal {C}},[y]_{\mathcal {C}})\ll '_{i}([w']_{\mathcal {C}},[v']_{\mathcal {C}})\), by the construction of \(\mathscr {R}'\). Since \([w']_{\mathcal {C}}=[w]_{\mathcal {C}}\) and \([v']_{\mathcal {C}}=[v]_{\mathcal {C}}\), it follows that \(([x]_{\mathcal {C}},[y]_{\mathcal {C}})\ll '_{i}([w]_{\mathcal {C}},[v]_{\mathcal {C}})\), and therefore \(([w]_{\mathcal {C}},[v]_{\mathcal {C}})\notin \min _{\ll '_{i}}{ R}'_{i}\). \(\square \)
Lemma 6
(Satisfaction preservation) Let  be finite and closed under subsentences, let \(\mathscr {R}=\langle { W},{ R},{ V},\ll \rangle \) be an \({ R}\)-ordered model, and let \(\mathscr {R}'=\langle { W}',{ R}',{ V}',\ll ' \rangle \) be the \(\mathcal {C}\)-filtration of \(\mathscr {R}\). For every \(w\in { W}\) and every \(\alpha \in \mathcal {C}\), \(\mathscr {R},w\Vdash \alpha \) if and only if \(\mathscr {R}',[w]_{\mathcal {C}}\Vdash \alpha \).
be finite and closed under subsentences, let \(\mathscr {R}=\langle { W},{ R},{ V},\ll \rangle \) be an \({ R}\)-ordered model, and let \(\mathscr {R}'=\langle { W}',{ R}',{ V}',\ll ' \rangle \) be the \(\mathcal {C}\)-filtration of \(\mathscr {R}\). For every \(w\in { W}\) and every \(\alpha \in \mathcal {C}\), \(\mathscr {R},w\Vdash \alpha \) if and only if \(\mathscr {R}',[w]_{\mathcal {C}}\Vdash \alpha \).
Proof
The proof is by induction on the structure of the sentence \(\alpha \). Below we only show the case of  via its dual
via its dual  . (The classical cases are as usual.)
. (The classical cases are as usual.)
Assume  . Since \(\mathcal {C}\) is closed, we have \(\beta \in \mathcal {C}\), and thus the induction hypothesis applies to \(\beta \).
. Since \(\mathcal {C}\) is closed, we have \(\beta \in \mathcal {C}\), and thus the induction hypothesis applies to \(\beta \).
For the only-if part, let  . Then there is \(w'\in { W}\) such that \((w,w')\in { R}_{i}\), \((w,w')\in \min _{\ll _{i}}{ R}_{i}^{w}\) and \(\mathscr {R},w'\Vdash \beta \). We have \(([w]_{\mathcal {C}},[w']_{\mathcal {C}})\in { R}'_{i}\), since \(w\in [w]_{\mathcal {C}}\) and \(w'\in [w']_{\mathcal {C}}\). By induction, we get \(\mathscr {R}',[w']_{\mathcal {C}}\Vdash \beta \). By Lemma 5, \(([w]_{\mathcal {C}},[w']_{\mathcal {C}})\in \min _{\ll '_{i}}{ R}_{i}^{[w]_{\mathcal {C}}}\). Hence
. Then there is \(w'\in { W}\) such that \((w,w')\in { R}_{i}\), \((w,w')\in \min _{\ll _{i}}{ R}_{i}^{w}\) and \(\mathscr {R},w'\Vdash \beta \). We have \(([w]_{\mathcal {C}},[w']_{\mathcal {C}})\in { R}'_{i}\), since \(w\in [w]_{\mathcal {C}}\) and \(w'\in [w']_{\mathcal {C}}\). By induction, we get \(\mathscr {R}',[w']_{\mathcal {C}}\Vdash \beta \). By Lemma 5, \(([w]_{\mathcal {C}},[w']_{\mathcal {C}})\in \min _{\ll '_{i}}{ R}_{i}^{[w]_{\mathcal {C}}}\). Hence  .
.
For the if part, let  . Then there is \([v]_{\mathcal {C}}\in { W}'\) such that \(([w]_{\mathcal {C}},[v]_{\mathcal {C}})\in { R}'_{i}\), \(([w]_{\mathcal {C}},[v]_{\mathcal {C}})\in \min _{\ll '_{i}}{{ R}'_{i}}^{[w]_{\mathcal {C}}}\) and \(\mathscr {R}',[v]_{\mathcal {C}}\Vdash \beta \). By induction, we get \(\mathscr {R},v\Vdash \beta \). Moreover, by Lemma 5, there are \(w'\in [w]_{\mathcal {C}}\) and \(v'\in [v]_{\mathcal {C}}\) such that \((w',v')\in \min _{\ll _{i}}{ R}_{i}^{w'}\), from which follows \((w',v')\in { R}_{i}\). Since \(v\simeq _{\mathcal {C}}v'\) and \(\beta \in \mathcal {C}\), \(\mathscr {R},v\Vdash \beta \) implies \(\mathscr {R},v'\Vdash \beta \). Hence we have
. Then there is \([v]_{\mathcal {C}}\in { W}'\) such that \(([w]_{\mathcal {C}},[v]_{\mathcal {C}})\in { R}'_{i}\), \(([w]_{\mathcal {C}},[v]_{\mathcal {C}})\in \min _{\ll '_{i}}{{ R}'_{i}}^{[w]_{\mathcal {C}}}\) and \(\mathscr {R}',[v]_{\mathcal {C}}\Vdash \beta \). By induction, we get \(\mathscr {R},v\Vdash \beta \). Moreover, by Lemma 5, there are \(w'\in [w]_{\mathcal {C}}\) and \(v'\in [v]_{\mathcal {C}}\) such that \((w',v')\in \min _{\ll _{i}}{ R}_{i}^{w'}\), from which follows \((w',v')\in { R}_{i}\). Since \(v\simeq _{\mathcal {C}}v'\) and \(\beta \in \mathcal {C}\), \(\mathscr {R},v\Vdash \beta \) implies \(\mathscr {R},v'\Vdash \beta \). Hence we have  . Since
. Since  , we get
, we get  . \(\square \)
. \(\square \)
Lemma 7
If  is satisfiable, then it has a finite model.
is satisfiable, then it has a finite model.
Proof
Let \(\mathscr {R}\) be such that \(\mathscr {R}\Vdash \alpha \), and let \(\mathcal {C}={\text { sub}(\alpha )}\). From finiteness of \(\alpha \), it follows that \(\mathcal {C}\) is finite, too. Hence Definition 18 guarantees the existence of a \(\mathcal {C}\)-filtration \(\mathscr {R}'\) of \(\mathscr {R}\) having a finite set of worlds. It remains to show that \(\mathscr {R}'\) is a model of \(\alpha \). Let \(w\in { W}\) be such that \(\mathscr {R},w\Vdash \alpha \). Since \(\alpha \in \mathcal {C}\), by Lemma 6 it follows that \(\mathscr {R}',[w]_{\mathcal {C}}\Vdash \alpha \). \(\square \)
Rights and permissions
About this article
Cite this article
Britz, K., Varzinczak, I. Preferential Accessibility and Preferred Worlds. J of Log Lang and Inf 27, 133–155 (2018). https://doi.org/10.1007/s10849-017-9264-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-017-9264-0



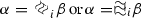 , then
, then