Striola magica. A functional explanation of otolith geometry

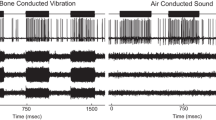
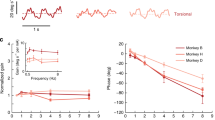
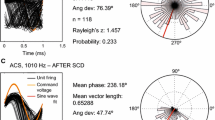
Abstract

Otolith end organs of vertebrates sense linear accelerations of the head and gravitation. The hair cells on their epithelia are responsible for transduction. In mammals, the striola, parallel to the line where hair cells reverse their polarization, is a narrow region centered on a curve with curvature and torsion. It has been shown that the striolar region is functionally different from the rest, being involved in a phasic vestibular pathway. We propose a mathematical and computational model that explains the necessity of this amazing geometry for the striola to be able to carry out its function. Our hypothesis, related to the biophysics of the hair cells and to the physiology of their afferent neurons, is that striolar afferents collect information from several type I hair cells to detect the jerk in a large domain of acceleration directions. This predicts a mean number of two calyces for afferent neurons, as measured in rodents. The domain of acceleration directions sensed by our striolar model is compatible with the experimental results obtained on monkeys considering all afferents. Therefore, the main result of our study is that phasic and tonic vestibular afferents cover the same geometrical fields, but at different dynamical and frequency domains.

Mathematical appendix

This appendix provides the mathematical definitions, theorems and proofs, underlying our Striola model. In particular it describes the virtual surface generated by a twisted curve in the Euclidian space and the optimal shapes of curves allowing an uniform detection of acceleration directions.

The suggested information processing of the striolar region on the otoliths macula lays on the correspondence between the pairs of points of a space curve and the directions orthogonal to the tangents at the points. The shape of the striola is dictated by the range and the regularity of this correspondence, thus we will conduct a study of its properties. In Section A.1 we show that the regularity depends on the existence of curvature and torsion. This gives an elementary introduction in the affine framework to the more sophisticated investigations of Sections A.2 and A.3.

Notations: we consider a smooth curve S in the three dimensional Euclidian space, and we study the correspondence between the pairs of points $(P_{1},P_{2})$ of S and the directions D that are orthogonal to S in $P_{1}$ and $P_{2}$. We are particularly interested in the case where this correspondence defines a mapping $D=F(P_{1},P_{2})$ for pairs of points $P_{1},P_{2}$ that are sufficiently closed in S. We will consider several natural measures of area on the set of pairs of points on S and on the set of directions in the space. The regularity and uniformity of the mapping F is encoded by its jacobian determinant J, then we will study the link between J and the geometry of S. From the Euclidian point of view it is natural to retain on the set of points pairs, the measure associated to the canonical coordinates $(\sigma _{1},\sigma _{2})$, where $\sigma _{1}=s_{1}+s_{2}$ and $\sigma _{2}=s_{1}s_{2}$ are the elementary symmetric functions of the curvilinear abscissas $s_{1},s_{2}$ of the respective points $P_{1},P_{2}$ on S, and on the set of directions D the measure given by solid angle; this is the framework of Section A.2. In Section A.3 we restrict our attention to the case of a spherical curve S, for application to our model of the striola curve. However ,we begin in Section A.1 with the Cartesian point of view, where computations are more elementary. In this case a natural parametrization for points on S comes from the orthogonal projection on one axis and natural coordinates for directions in the space come from the intersection with a fixed plane. (Figs. 13 and 14)

Fig. 13

Representation of the preferred direction encoded by each couples of cells. It is here computed for the curve $x(t)=t/\sqrt (2), y=t^{2}, z = \sqrt (2)/3 \times t^{3}$, for $t \in [-10;10]$, with 25 cells distributed equally along t. Panels show the projection of this surface in the $(x,y)$, $(y,z)$ and $(x,z)$ planes, the color palette represents the value of missing component (z, x and y respectively)

Fig. 14

Representation of the virtual surface $\Sigma$, defined by Eq. (34–36), whose normals define the perceived directions. It is here computed for the curve $x(t)=t/\sqrt (2), y=t^{2}, z = \sqrt (2)/3 \times t^{3}$, for $t \in [-10;10]$. Panels show the projection of this surface in the $(x,y)$, $(z,y)$ and $(x,z)$ planes, as well as in an arbitrary plane, the color palette represents the same z value in each of the panels

1.1 A.1 Cartesian optimal striola

Let us consider a space curve S described in parametric form by cartesian coordinates

$$ x=f(t),\quad y=g(t),\quad z=h(t). $$

(32)

If a vector $\overrightarrow {A}$ has coordinates $u,v,w$, its scalar product with the tangent $\overrightarrow {T}$ of S is given by

$$ \overrightarrow{A}.\overrightarrow{T}=f'(t)u+g'(t)v+h'(t)w. $$

(33)

The orthogonality equation $\overrightarrow {A}.\overrightarrow {T}=0$ gives

$$ f'(t)u+g'(t)v+h'(t)w=0. $$

(34)

We suppose that $\overrightarrow {T}$ is nowhere 0, and that there exist a conical domain of $\overrightarrow {A}$ where the Eq. (34) has two solutions $t_{1}(u,v,w)$, $t_{2}(u,v,w)$ (eventually equals). In this case, for each $\overrightarrow {A}$ in the domain, there exist two parameters $t_{1},t_{2}$ and a non-zero real number c such that

$$ c\overrightarrow{A}=\overrightarrow{T}(t_{1})\times\overrightarrow{T}(t_{2}), $$

(35)

which translates in coordinates as

$$cu=g'(t_{1})h'(t_{2})-g'(t_{2})h'(t_{1}),$$

(36)

$$cv=h'(t_{1})f'(t_{2})-h'(t_{2})f'(t_{1}),$$

(37)

$$cw=f'(t_{1})g'(t_{2})- f'(t_{2})g'(t_{1}).$$

(38)

A classical theorem asserts that any smooth function $\varphi$ (resp. polynomial function) of two real variables $t_{1},t_{2}$ (defined in a domain of the plane which is symmetric with respect to the diagonal $t_{1}=t_{2}$) which satisfies $\varphi (t_{1},t_{2})=\varphi (t_{2},t_{1})$ for any pair $(t_{1},t_{2})$, is equal to a smooth (resp. polynomial) function $\Phi (\sigma _{1},\sigma _{2})$ where $\sigma _{1}=t_{1}+t_{2}$ and $\sigma _{2}=t_{1}t_{2}$ are the elementary symmetric functions of $t_{1}$ and $t_{2}$.In addition we can suppose that one of the coordinates $u,v,w$ can be arbitrarily chosen, say for instance $w=1$. Then we get a transformation F from a domain of $(\sigma _{1},\sigma _{2})$ to a domain of $(u,v)$. Let us denote $J(\sigma _{1},\sigma _{2})$ the jacobian determinant of the transformation F.

Theorem 1

Let us suppose that J is regular and non-vanishing in the neighborhood of a point (0,0) corresponding to a pair of coincident points, then it exists an Euclidian affine change of coordinates $x,y,z$ , where we have $f(0)=0$, $f'(0)\neq 0$, $g(0)=g'(0)=0$ but $g''(0)\neq 0$ , and $h(0)=h'(0)=h''(0)=0$ but $h^{(3)}\neq 0$. In other terms, after an Euclidian affine change of frame, the valuations of the Taylor series of g and h are the same as the ones of the twisted cubic.

Proof

We begin by fixing the x axis in such a way that $f(0)=0$, $f'(0)\neq 0$. We change the parametrization t to have $f(t)=at$ in a neighborhood of $t=0$. It is easy to show this has no effect on the conclusions of the theorem. We suppose $w=1$. In the considered domain of $u,v$ there exist two solutions $t_{1}(u,v)$, $t_{2}(u,v)$ (eventually equals) of the orthogonality equation, that is:

$$ au+g'(t_{1})v+h'(t_{1})=0,\quad\quad au+g'(t_{2})v+h'(t_{2})=0. $$

(39)

By solving this linear system we obtain $u,v$ from $t_{1},t_{2}$:

$$u=\frac{h'(t_{2})g'(t_{1})-h'(t_{1})g'(t_{2})}{a(g'(t_{2})-g'(t_{1}))},$$

(40)

$$v=\frac{h'(t_{1})-h'(t_{2})}{g'(t_{2})-g'(t_{1})}.$$

(41)

On another side, by the implicit function theorem we have

$$(g''(t_{1})v+h''(t_{1}))\frac{\partial t_{1}}{\partial u}=-a,$$

(42)

$$(g''(t_{1})v+h''(t_{1}))\frac{\partial t_{1}}{\partial v}=-g'(t_{1}),$$

(43)

and similar equations for $t_{2}$. Thus the jacobian determinant of the transformation from $t_{1},t_{2}$ to $u,v$ is equal to

$$\begin{array}{rll} J'(u,v;t_{1},t_{2})&=&a^{-1}(g'(t_{2})-g'(t_{1}))^{-1}(g''(t_{1})v+h''(t_{1}))\\ &&\quad \times (g''(t_{2})v+h''(t_{2})) \end{array} $$

(44)

We remark that where $t_{1}=t_{2}$, the function $J'$ has a priori a simple zero $(t_{1}-t_{2})$ along the diagonal subset. However the jacobian of the transformation which maps $(t_{1},t_{2})$ to $(\sigma _{1},\sigma _{2})$ is equal to $t_{1}-t_{2}$, so the jacobian of the mapping F in the coordinates $u,v$ and $\sigma _{1},\sigma _{2}$ is given by the regular symmetric function

$$\begin{array}{rll} J(\sigma_{1},\sigma_{2})&=&[a(t_{1}-t_{2})(g'(t_{2})-g'(t_{1}))]^{-1}\\ &&\quad \times (g''(t_{1})v+h''(t_{1}))(g''(t_{2})v+h''(t_{2}))\\ \end{array} $$

(45)

that is in general finite and non-zero along the diagonal.

Let us suppose that J is a smooth function without zero in an open set of $(t_{1},t_{2})$ containing (0,0). By substitution of the values of u and v we obtain the following functional equation for g and h:

$$\begin{array}{lll} &&[g''(t_{1})(h'(t_{1})-h'(t_{2}))+h''(t_{1})(g'(t_{2})-g'(t_{1}))]\\ &&[g''(t_{2})(h'(t_{1})-h'(t_{2}))+h''(t_{2})(g'(t_{2})-g'(t_{1}))]\\&&\quad=J(t_{1},t_{2})a(t_{1}-t_{2})(g'(t_{2})-g'(t_{1}))^{3},\end{array}$$

(46)

Let us suppose that $t_{1}$ and $t_{2}$ both approach t, in such a manner that $t=\alpha t_{1}+\beta t_{2}$ with $\alpha ,\beta$ bounded and $\alpha +\beta =1$. Up to the order 4 in $t_{2}-t_{1}$ (or $t_{1}-t$ or $t_{2}-t$ because it is the same order) we have

$$\begin{array}{lll}&&[((t_{1}-t)(t_{1}-t_{2})+\frac{1}{2}(t_{2}-t_{1})(t_{1}+t_{2}-2t))h''(t)g^{(3)}(t))\\&&\;\;+((t_{1}-t)(t_{2}-t_{1})+\frac{1}{2}(t_{1}-t_{2})(t_{1}+t_{2}-2t))h^{(3)}(t)g''(t))]\\ &&[((t_{2}-t)(t_{1}-t_{2})+\frac{1}{2}(t_{2}-t_{1})(t_{1}+t_{2}-2t))h''(t)g^{(3)}(t))\\&&\;\;+((t_{2}-t)(t_{2}-t_{1})+\frac{1}{2}(t_{1}-t_{2})(t_{1}+t_{2}-2t))h^{(3)}(t)g''(t))]\\&&\qquad=-a J(t,t)(t_{1}-t_{2})^{4}g''(t)^{3},\end{array}$$

(47)

We also have $t_{1}-t=\beta (t_{1}-t_{2}), t_{2}-t=\alpha (t_{2}-t_{1}), t_{1}+t_{2}-2t=(2\beta -1)(t_{1}-t_{2})$, then, at the limit, we get

$$\begin{array}{lll}&&\left[\frac{1}{2}h''(t)g^{(3)}(t))-\frac{1}{2}h^{(3)}(t)g''(t))\right]\\&& \left[-\frac{1}{2}h''(t)g^{(3)}(t))+\frac{1}{2}h^{(3)}(t)g''(t))\right]\\&&\qquad\qquad\quad=-a J(t,t)g''(t)^{3}.\end{array}$$

(48)

We would have found the same formula by fixing $t_{1}=t$ and looking at $t_{2}$ tending to t.

Let us write $G=g''$ and $H=h''$, we obtain

$$ (G'H-GH')^{2}=4aJG^{3}, $$

(49)

From this we see that G cannot vanish, meaning that g is necessarily convex or concave. By changing the sign of the coordinate y in the ambient space, we can suppose that g is convex, then G is positive and J positive.

By using a translation and a rotation in the plane $x,y$ we can suppose that $g(0)=g'(0)=0$, but $g''(0)=G(0)> 0$, which gives a development

$$ g(t)=\frac{1}{2}bt^{2}+\frac{1}{3}b_{1}t^{3}+... $$

(50)

When g is known as well as the initial condition $H(0)=h''(0)$, the linear differential equation

$$ H'=(G'/G)H+2(aGJ)^{1/2}, $$

(51)

determines H as

$$ H(t)=G(t)\frac{H(0)}{G(0)}+2G(t)\int_{0}^{t}\sqrt{\frac{aJ(s)}{G(s)}}ds. $$

(52)

Then, knowing the values of $h(0),h'(0)$ in addition to $h''(0)$, we obtain h by two other quadratures.

With a vertical translation we can assume $h(0)=0$, and with a rotation in the plane $x,z$ we can assume $h'(0)=0$. By rotating the plane $y,z$ we can then make $h''(0)=0$. Now we can apply the formula (52) and the Theorem 1 follows.

When $f,g,h$ satisfy the conclusions of the Theorem 1, the axis $x,y,z$ are respectively aligned with the tangent, the normal and the binormal axis of the curve S at the origin point 0. The curvature $\kappa (0)$ and the torsion $\tau (0)$ of S in 0 are given by

$$ \kappa(0)=\frac{g''(0)}{f'(0)^{2}},\quad \tau(0)=-\frac{h^{(3)}(0)}{f'(0)g''(0)}. $$

(53)

Let us verify by direct computation that every polynomials $g,h$ of respective degree 2 and 3 satisfy the formula (46) for all points $(t_{1},t_{2})$ with J a non-zero constant:We can write

$$\begin{array}{rll}f(t)&=&at,\; g(t)\\ &=&\frac{b}{2}t^{2}+b_{1}t+b_{0},\quad h(t)=\frac{c}{3}t^{3}+c_{2}t^{2}+c_{1}t+c_{0},\end{array} $$

(54)

then we have

$$g'(t_{2})-g'(t_{1})=b(t_{2}-t_{1}),$$

(55)

$$h'(t_{1})-h'(t_{2})=c(t_{1}-t_{2})(t_{2}+t_{1})+2c_{2}(t_{1}-t_{2}),$$

(56)

$$g''(t)=b,$$

(57)

$$h''(t)=2(ct+c_{2}),$$

(58)

then

$$g''(t_{1})(h'(t_{1}) - h'(t_{2})) + h''(t_{1})(g'{\kern-1pt}(t_{2})-g'(t_{1})) = -bc(t_{2}-t_{1})^{2},$$

(59)

$$g''(t_{2})(h'(t_{1})-h'(t_{2})) + h''(t_{2})(g'(t_{2})-g'(t_{1})) = bc(t_{2}-t_{1})^{2},$$

(60)

$$(t_{2}-t_{1})(g'(t_{2})-g'(t_{1}))^{3} = b^{3}(t_{2}-t_{1})^{4},$$

(61)

and Eq. (46) is satisfied with

$$ \frac{b^{2}c^{2}}{b^{3}}=aJ, $$

(62)

that is

$$ J=\frac{c^{2}}{ab}. $$

(63)

□

Theorem 2

Suppose that $f,g,h$ satisfy the conclusions of the Theorem 1, and that f is a linear function of t; then J is constant in the neighborhood of the diagonal if and only if g is a polynomial of degree 2 and h is a polynomial of degree 3.

Proof

Let us fix the constant J and the parameter $t_{2}$; the two Eqs. (46) and (49) constitute a system of two non autonomous ordinary differential equations in two unknown functions $g',h'$ of order one in $g'$ and order two in $h'$, so by the Cauchy-Lipschitz theorem, the general solution depends on three independent real parameters when the initial time is chosen, thus the general solution of the system when initial time is let free depends on four real constants. But we already know solutions of the system depending on four real parameters, they are polynomials in t of degree 1 for $g'$ and of degree 2 for $h'$. CQFD.

Thus, in the case of Theorem 1, we obtain a semi-cubic parabola

$$ x=at,\quad y=\frac{1}{2}a^{2}\kappa(0)t^{2},\quad z=-\frac{1}{6}a^{3}\kappa(0)\tau(0)t^{3}. $$

(64)

□

1.2 A.2 Euclidian optimal striola

The natural measure on directions in a 3D Euclidian space is the solid angle $d\sigma$, and the natural parametrization of a curve is by its arc-length s. Therefore it is natural to look at the correspondence between pairs of points and directions in these coordinates. We will first establish a formula for the Jacobian determinant in these coordinates. As before we will constat it has a simple zero. As in the Cartesian study, the symmetric coordinates operate a regularization. But the new ingredient here is the surface obtained by translating the curve by itself, that was considered by Sophus Lie, for application to minimal surfaces. The points on this auxiliary surface form another symmetric parametrization of pairs of points, giving another natural regularization.

Let us introduce a surface $\Sigma$ associated to the curve S, it is formed by adding the pair of points of the curve:

$$x(s_{1},s_{2})=f(s_{1})+f(s_{2}),$$

(65)

$$y(s_{1},s_{2})=g(s_{1})+g(s_{2}),$$

(66)

$$z(s_{1},s_{2})=h(s_{1})+h(s_{2}).$$

(67)

Let us denote by $P_{1},P_{2}$ the points of abscissas $s_{1},s_{2}$ respectively on the curve S. By fixing $s_{2}$ (resp. $s_{1}$) we see that the tangent vector $\overrightarrow {T_{1}}$ (resp. $\overrightarrow {T_{2}}$)to S in $P_{1}$ (resp. $P_{2}$) is tangent to the surface $\Sigma$. Then the cross product $\overrightarrow {T_{1}}\times \overrightarrow {T_{2}}$ is normal to $\Sigma$. Thus for generic points, when $\overrightarrow {T_{1}}$ and $\overrightarrow {T_{2}}$ are not collinear, the unit normal vector $\overrightarrow {n}$ to $\Sigma$ at the point corresponding to $(s_{1},s_{2})$ is parallel to the intersection of the normal planes at S in $P_{1}$ and $P_{2}$. This is the way $\Sigma$ represents the pair of points $(P_{1},P_{2})$ on S, by developing their associated direction D in the space.

This surface $\Sigma$ is a particular case or a “Translation Surface”, in the sense of S. Lie, H. Poincaré, G. Darboux (Leçons sur la Théorie gé né rale des Surfaces et les applications gé omé triques du Calcul Infinité simal; Part I, L.III, ch. VI, VII, VIII, IX; (Darboux 1887)). The general translation surfaces are the surfaces described by the sum of points of two given space curves. In our case, the curve is translated by itself.

Note that the surface which is defined as the locus of middle points of the segments that join the pairs of points of the curve S, is the surface homothetic to $\Sigma$ in the ratio $1/2$, then it has the same normals and could be used in the place of $\Sigma$ in what follows.

According to Lie, by using imaginary parameters, any minimal surface is described as a translation surface starting from a complex curve with tangent vectors of zero lengths.

Caution: the surface $\Sigma$ does not represent the macula, it represents the directions of acceleration detected by the striola by its normal vectors. It is a kind of virtual macula associated to the striola. The parametrization by $s_{1},s_{2}$ is singular, because two pairs $(s_{1},s_{2})$ and $(s_{2},s_{1})$ represent the same point, but the surface $\Sigma$ itself is in general regular. Let us see what happens in the example of the surface generated by the twisted cubic; in this case we have:

$$x(t_{1},t_{2})=t_{1}+t_{2},$$

(68)

$$y(t_{1},t_{2})=t_{1}^{2}+t_{2}^{2},$$

(69)

$$z(t_{1},t_{2})=t_{1}^{3}+t_{2}^{3}.$$

(70)

We then have

$$ z-xy=t_{1}t_{2}^{2}+t_{2}t_{1}^{2}=x(t_{1}t_{2})=\frac{1}{2}x(x^{2}-y), $$

(71)

so $\Sigma$ is included in the smooth graph of a polynomial function:

$$ z=\frac{1}{2}x(y+x^{2}). $$

(72)

And it is easy to show that every point $(x,y,z)$ in this graph such that $y\geq x^{2}/2$ belongs to $\Sigma$. Again the parametrization problem comes from the symmetry between $t_{1}$ and $t_{2}$, but the regular prolongation comes from the fact that every symmetric polynomial of $t_{1},t_{2}$, like $t_{1}^{3}+t_{2}^{3}$, is a function of $x=t_{1}+t_{2}$ and $y=t_{1}^{2}+t_{2}^{2}$. (This theorem needs rational coefficients, integers are not sufficient are they were for $t_{1}+t_{2}$ and $t_{1}t_{2}$, but this has no consequence in the present context.) As the example of twisted cubic shows, the set of directions that are detected by real parameters $t_{1},t_{2}$ is the set of normals of a regular surface with boundary.

For the general twisted cubic

$$ x=at,\quad y=\frac{b}{2}t^{2},\quad z=\frac{c}{3}t^{3} $$

(73)

we find the region $y\geq bx^{2}/4a^{2}$ on the gather surface

$$ z=\frac{c}{6a^{3}b}(bx^{3}+2a^{2}xy). $$

(74)

In what follows, the numbers $s_{1},s_{2}$ will design arc-lengths on the curve S. We denote by $\overrightarrow {T_{1}}$ resp. $\overrightarrow {T_{2}}$ the unit tangent to the curve S at $s_{1}$ resp. $s_{2}$. Let us suppose they are linearly independent and denote by $\overrightarrow {n}$ the unit normal to the plane they generate, such that $(\overrightarrow {T_{1}},\overrightarrow {T_{2}},\overrightarrow {n})$ constitute a right handed oriented reference frame, which corresponds to the vector product formula: $|\sin (arcos(\overrightarrow {T_{1}}.\overrightarrow {T_{2}}))|\overrightarrow {n}=\overrightarrow {T_{1}}\times \overrightarrow {T_{2}}$.

For any surface in $\mathbb {R}^{3}$ the Gauss mapping is the map to the unit sphere, which sends a point to the unit normal of the surface in this point, thus in our case the Gauss mapping $\gamma$ sends the point of $\Sigma$ corresponding to $s_{1},s_{2}$ onto the vector $\overrightarrow {n}$. This map is specially interesting for us because $\overrightarrow {n}$ represents the preferred direction of acceleration of an afferent cell associated to the parameters $(s_{1},s_{2})$.

By a theorem of Gauss, the determinant of the jacobian of $\gamma$ from orthonormal coordinates on $\Sigma$ to solid angle is the Gauss curvature function K of the surface $\Sigma$.

The Riemannian metric on $\Sigma$ has coefficients $g_{ij}$ defined by the scalar products $\overrightarrow {T_{i}}.\overrightarrow {T_{j}}$, cf. Coxeter, Introduction to Geometry (Wiley, 1969). In our case $g_{11}=g_{22}=1$. The superficial area measure is given in these coordinates by the formula

$$ dA=\sqrt{g}ds_{1}ds_{2}, $$

(75)

where we noted

$$ g=g_{11}g_{22}-g_{12}^{2}=1-(\overrightarrow{T_{1}}.\overrightarrow{T_{2}})^{2} $$

(76)

Observe that the two families of curves respectively defined by fixing $s_{1}+ s_{2}$ or $s_{1}-s_{2}$ equal to constants, are orthogonal one to each other.

We denote by $g^{ij}$ the coefficients of the inverse matrix of $(g_{ij})$; they are

$$ g^{11}=g^{22}=g^{-1},\quad g^{12}=g^{21}=-g^{-1}g_{12}. $$

(77)

The first Christoffel symbols (describing the intrinsic parallel transport on the surface) are defined as

$$ \Gamma_{ij;k}=\frac{1}{2}(\partial_{i}g_{jk}+\partial_{j}g_{ik}-\partial_{k}g_{ij}). $$

(78)

In our case the only non-zero symbols are

$$ \Gamma_{11;2}=\partial_{1}(g_{12}),\quad\Gamma_{22;1}=\partial_{2}(g_{12}). $$

(79)

The second (and more usual) Christoffel symbols are defined as

$$ \Gamma^{k}_{ij}=\sum g^{kl}\Gamma_{ij;k}. $$

(80)

Thus in our case they are non-zero only if $i=j$. All the non-zero symbols are given by:

$$\Gamma_{11}^{1}=\frac{-g_{12}\partial_{1}(g_{12})}{g},\quad\Gamma_{11}^{2}=\frac{\partial_{1}(g_{12})}{g},$$

(81)

$$\Gamma_{22}^{1}=\frac{\partial_{2}(g_{12})}{g},\quad\Gamma_{22}^{2}=\frac{-g_{12}\partial_{2}(g_{12})}{g}, $$

(82)

It is useful, in our case, to relate these intrinsic quantities with the parametric representation; for that we introduce the second derivatives vectors

$$ \overrightarrow{T_{ij}}=\frac{\partial}{\partial s_{j}}\overrightarrow{T_{i}}; $$

(83)

Then the Christoffel symbols are given by scalar products as

$$ \Gamma_{ij;k}=\overrightarrow{T_{k}}.\overrightarrow{T_{ij}} $$

(84)

We can also define

$$ b_{ij}=\overrightarrow{n}.\overrightarrow{T_{ij}}. $$

(85)

They are the coefficients of the second fundamental form of $\Sigma$. In our present case only $b_{11}$ and $b_{22}$ could be non-zero. The corresponding Weingarten coefficients are

$$ b^{i}_{j}=\sum g^{ik}b_{kj}, $$

(86)

thus, in our case

$$ b^{1}_{1}=g^{-1}b_{11},\quad b^{2}_{2}=g^{-1}b_{22},\quad b^{1}_{2}=b^{2}_{1}=-g^{-1}g_{12}b_{12}. $$

(87)

Then we obtain the “equations of Gauss”:

$$ \overrightarrow{T_{ij}}=\sum \Gamma^{k}_{ij}\overrightarrow{T_{k}}+b_{ij}\overrightarrow{n}. $$

(88)

If we denote by b the discriminant of the second fundamental form

$$ b=b_{11}b_{22}-b_{12}^{2}, $$

(89)

the Gauss curvature is defined by

$$ K=\frac{b}{g}. $$

(90)

The Theorema egregium of Gauss says that K can be expressed by the derivatives of the second symbols. A nice formula was found by Liouville (cf. Coxeter p.367):

$$ \sqrt{g}K=\frac{\partial}{\partial s_{2}}\left(\frac{\sqrt{g}}{g_{11}}\Gamma_{11}^{2}\right) -\frac{\partial}{\partial s_{1}}\left(\frac{\sqrt{g}}{g_{11}}\Gamma_{12}^{2}\right) $$

(91)

Note, in our case we have $\Gamma _{12}^{2}=0$, and

$$ \Gamma_{11}^{2}=\frac{\overrightarrow{T_{11}}.\overrightarrow{T_{2}}}{g}. $$

(92)

(This is because $\overrightarrow {T_{11}}$ is orthogonal to $\overrightarrow {T_{1}}$.)

The Gauss map has the curvature as its jacobian determinant:

$$ \frac{d\sigma}{\sqrt{g}ds_{1}ds_{2}}=K, $$

(93)

Thus the jacobian determinant from $ds_{1}ds_{2}$ to $d\sigma$ is given by

$$ J'=\sqrt{g}K=\frac{\partial}{\partial s_{2}}\frac{\overrightarrow{T_{11}}.\overrightarrow{T_{2}}}{\sqrt{g}} $$

(94)

Which can be rewritten as

$$ J'=\frac{(\overrightarrow{T_{1}}.\overrightarrow{T_{2}})(\overrightarrow{T_{11}}.\overrightarrow{T_{2}}) (\overrightarrow{T_{22}}.\overrightarrow{T_{1}}) +g(\overrightarrow{T_{11}}.\overrightarrow{T_{22}})}{g^{3/2}} $$

(95)

From Section A.1 we know that $J'$ has a simple zero along the diagonal (of the first order like $(s_{1}-s_{2})$ multiplied by a constant). This invitees to make a re-normalization of $J'$. A natural choice is to divide by $s_{1}-s_{2}$ because this is the jacobian of the transformation from the coordinates $(s_{1},s_{2})$ to the elementary symmetric function $\sigma _{1}=s_{1}+s_{2}, \sigma _{2}=s_{1}s_{2}$. But also $\sqrt {g}$ has a first order zero on the diagonal $s_{1}=s_{2}$, then an alternative natural choice to re-normalize $J'$ is to take the curvature K itself. This corresponds to the representation of the set of pairs of points on S by the surface $\Sigma$ itself. With this second choice, the optimality problem becomes: to find the curves S such that the associated double surface of translation $\Sigma$ has the less possible changing Gaussian curvature. We will compute now this curvature K, and the density $\sqrt {g}$.

The jacobian of the mapping from affine coordinates $(u,v,1)$ on directions to the spherical angle measure is given by

$$ J(u,v;\sigma)=\frac{1}{\sqrt{1+u^{2}+v^{2}}}, $$

(96)

where $u,v$ are given in function of $s_{1},s_{2}$ by the formulas

$$u=\frac{g_{1}h_{2}-h_{1}g_{2}}{f_{1}g_{2}-g_{1}f_{2}}$$

(97)

$$v=\frac{h_{1}f_{2}-f_{1}h_{2}}{f_{1}g_{2}-g_{1}f_{2}}$$

(98)

For computation another formula is helpful, coming from Weingarten (see Coxeter 1969 p.354):

$$ \sqrt{g}K=\left[\overrightarrow{n};\partial_{1}\overrightarrow{n};\partial_{2}\overrightarrow{n}\right], $$

(99)

where the bracket denotes the determinant of vectors, or triple product. In fact this Weingarten formula is the origin of the recalled Liouville formula. In our present situation the formula can be rewritten by using vector products as follows:

$$ g^{2}K=\left[\overrightarrow{T_{1}}\times \overrightarrow{T_{2}}; \overrightarrow{T_{11}} \times \overrightarrow{T_{2}}; \overrightarrow{T_{1}}\times \overrightarrow{T_{22}}\right] $$

(100)

Theorem 3

Let us denote by $\kappa ,\tau$ the curvature and torsion of S, and $\dot {\kappa },\dot {\tau }$ their derivatives with respect to the arc-length s on S; then along the double curve S on $\Sigma$ we have the limit formula

$$ K=-\frac{\tau^{2}}{4}. $$

(101)

At the first order in $s_{1}-s,s_{2}-s$, we have

$$ K(s_{1},s_{2})=-\frac{\tau^{2}}{4}\big[1+(s_{1}+s_{2}-2s)(\dot{\tau}/\tau)\big], $$

(102)

and

$$ g(s_{1},s_{2})=\kappa^{2}(s_{1}-s_{2})^{2}\big[1+(s_{1}+s_{2}-2s)(\dot{\kappa}/\kappa)\big]. $$

(103)

Proof

We use Taylor formula for evaluating $\overrightarrow {t_{1}},\overrightarrow {t_{2}}$, and recurrently all terms in the Eq. (100). (Note that we verified this result by using Eq. (90). The proof is a straightforward but tedious computation. As a corollary we obtain the amazing result that for twisted curves, when $\tau$ has no zero, the Gaussian curvature of the double surface is everywhere finite and strictly negative.

Theorem 3 is a precision of the Theorem 1, because it shows directly that a curve giving good vector detection in space must be twisted, but it uses the fact that curvature and torsion are well defined, which is one of the results of Theorem 1.

If we choose the surface $\Sigma$ as the natural parametrization of pairs of points $(P_{1},P_{2})$ on S, the absolute value of the Jacobian determinant from pairs of points to directions in space is approximatively given by

$$ |K|\approx \frac{1}{4}\tau^{2}(1+\frac{d(\ln (\tau))}{ds}(\sigma_{1}-2s)) $$

(104)

for near points, thus, at the first order of approximation, the optimal curves for uniform detection of directions must have a constant torsion $\tau$. But, if we choose the elementary symmetric functions $(\sigma _{1},\sigma _{2})$ as the natural parametrization of pairs of points $(P_{1},P_{2})$ on S, the absolute value of the Jacobian determinant for near points is given by

$$ |J|= \sqrt{g}|K|/|s_{1}-s_{2}|\approx\frac{1}{4}\kappa\tau^{2}(1+\frac{1}{2}\frac{d(\ln (\kappa\tau^{2}))}{ds}(\sigma_{1}-2s)). $$

(105)

Thus the optimal curves correspond to constant value of the quantity $\tau \sqrt {\kappa }$.

At higher orders in the formula of K it appears polynomials in the two variables $s_{1}-s_{2},s_{1}+s_{2}-2s$ whose coefficients are polynomials in the higher derivatives of $\kappa ,\tau$ with respect to s. At the order two for instance we obtain two coefficients of the following form

$$\begin{array}{lll}&&P(\kappa,\tau,\dot{\kappa},\dot{\tau},\ddot{\kappa},\ddot{\tau}) \\ &&\quad\quad=\kappa^{2}\tau^{2}\big[A\ddot{\kappa}/\kappa+B\ddot{\tau}/\tau+C(\dot{\kappa}/\kappa)^{2}+D(\dot{\tau}/\tau)^{2} \\&&\qquad\qquad\qquad +E(\dot{\kappa}\dot{\tau}/\kappa\tau)+F(\kappa^{2}+\tau^{2})\big]\end{array} $$

(106)

In particular, the only possibility that the order two computation of K gives a development $-\frac {\tau ^{2}}{4}\big [1+\alpha (s_{1}-s_{2})^{2}\big ]$ with a constant $\alpha$, is that $\kappa$ and $\tau$ are constants. That is S must be a circular helix.

The standard circular helix in the vertical cylinder of radius a is defined as

$$ x=a \cos t,\quad y=a\sin t,\quad z=ct. $$

(107)

One has

$$ \kappa=\frac{a}{a^{2}+c^{2}},\quad \tau=\frac{c}{a^{2}+c^{2}}, $$

(108)

$$ a=\frac{\kappa}{\kappa^{2}+\tau^{2}}. $$

(109)

(cf. Coxeter pp.323-325). The principal normal $\overrightarrow {p}=\dot {\overrightarrow {T}}/\kappa$ is always horizontal and its binormal $\textbf {b}$, as its tangent $\overrightarrow {T}$, makes a constant angle with the vertical. This binormal vector $\overrightarrow {b}$ is important for us because it is the limit for coincident points $P_{1},P_{2}$ of the normal vector $\overrightarrow {n}$ to the surface $\Sigma$.

In the case of helix we have the following formula for the curvature of $\Sigma$:

$$ K=-\frac{\tau^{2}}{4}\left[1+a\frac{\kappa}{2}(\cos(u_{1}-u_{2})-1)\right]^{-2}. $$

(110)

In perception, some acceleration directions $\overrightarrow {A}$ could be more natural than others. But, on directions in space, the 2D spherical Von-Mises distributions have maximum entropy among the laws when mean and variances are given; then it would be interesting to look at curves giving approximatively such laws for the preferred directions.

There is also a notion of generalized helix (cf. Coxeter p.325). They are the curves where the ration $\tau /\kappa$ has a constant value. They are characterized by the fact that their tangent vectors make a constant angle with a fixed vector. The standard twisted cubic is not a circular helix, but a linear transform of it is a generalized helix, that is $\tau /\kappa$ is a constant, and it has near its vertex a torsion and a curvature which are stationary. In fact let us consider the following special twisted cubic:

$$ x=\frac{t}{\sqrt{2}},\quad y=t^{2},\quad z=\frac{\sqrt{2}}{3}t^{3}; $$

(111)

then its curvature and torsion are given by

$$ \kappa=\tau=\frac{1}{(1+t^{2})^{2}} $$

(112)

(cf. Coxeter, exercise 17.8.2.) Note that a usual name for the twisted cubic (or rational normal curve) is rational helix. □

1.3 A.3 Spherical optimal striola

Our computational models of striola (cf. Methods) belong to a spherical surface M representing the macula. The normal vector $\overrightarrow {N}$ along the curve S which represents the polarization of hair cells disposed along S is the normal to the tangent vector $\overrightarrow {T}$ which is also tangent to the sphere M. The discussion in Section A.2 invites to consider as optimal the spherical curves with constant regularized jacobian determinant. We saw two natural choices; the first one, with algebraic coordinates as $(\sigma _{1}=s_{1}+s_{2}, \sigma _{2}=s_{1}s_{2})$ or any regular functions of these coordinates, gives a constant product $\kappa \tau ^{2}$; the second one with geometric parametrization by $\Sigma$, gives more simply a constant torsion $\tau$.

We suppose that M is part of the sphere in the $3D$ Euclidian space, centered in 0 of radius R. The variable point on the curve S is written now $X(s)$, where s denotes a curvilinear abscissa on S. By definition, we have

$$ \dot{X}=\overrightarrow{T},\quad \dot{\overrightarrow{T}}=\kappa \overrightarrow{p},\quad \dot{\overrightarrow{p}}=-\kappa \overrightarrow{T}+\tau \overrightarrow{b}. $$

(113)

Let us denote $C=1/\kappa$, $D=1/\tau$ the radius of curvature and the radius of torsion respectively. We have

$$ \overrightarrow{p}=C\ddot{X},\quad \dot{\overrightarrow{p}}=C\dddot{X}+\dot{C}\ddot{X}, $$

(114)

thus

$$ \overrightarrow{b}=\frac{1}{\tau}\dot{\overrightarrow{p}}+\frac{\kappa}{\tau}\overrightarrow{T} =DC\dddot{X}+D\dot{C}\ddot{X}+DC^{-1}\dot{X} $$

(115)

That gives the following formulas for the tangent, normal and binormal:

$$ \overrightarrow{T}=\dot{X},\quad \overrightarrow{p}=C\ddot{X},\quad \overrightarrow{b}=DC\dddot{X}+D\dot{C}\ddot{X}+DC^{-1}\dot{X} $$

(116)

As $X.X$ is constant equal to $R^{2}$, we have $X.\overrightarrow {T}=0$, and by derivation of this identity we get $\overrightarrow {T}.\overrightarrow {T}+\kappa X.\overrightarrow {p}=0$. But $\overrightarrow {T}$ has a norm equal to 1, thus we get $X.\overrightarrow {p}=-C$, or equivalently $X.\ddot {X}=-1$. By derivation again, we get $\dot {X}.\ddot {X}+X.\dddot {X}=0$, then $X.\dddot {X}=0$ because $\overrightarrow {T}$ and $\overrightarrow {p}$ are orthogonal. Then the scalar product $X.\overrightarrow {b}$ is equal to $D\dot {C}X.\ddot {X}$ that is $-D\dot {C}$. Thus

$$ X=-C\overrightarrow{p}-D\dot{C}\overrightarrow{b}, $$

(117)

and by equating the norm of X to R, this gives the well known intrinsic equation for spherical curves:

$$ C^{2}+D^{2}\dot{C}^{2}=R^{2}. $$

(118)

When D is constant, this equation has for only solutions

$$ C(s)=R\cos\left(\frac{s-s_{0}}{D}\right). $$

(119)

When $D\sqrt {C}$ is constant, equals to A, this equation has for solutions

$$ C(s)=R.cnl^{2}\left(\frac{R^{1/2}(s-s_{0})}{2A}\right), $$

(120)

where cnl denotes the lemniscate elliptic function coslemn, that inverses the lemniscate elliptic integral of Bernoulli and Fagnano:

$$ I(u)=\int_{u}^{1}\frac{dt}{\sqrt{1-t^{4}}} $$

(121)

With the Jacobi-Guderman notations we have $cnl(x)=cn(x\sqrt {2},1/\sqrt {2})$. (A nice reference for elliptic functions is Greenhill (1892))

The associated functions $\overrightarrow {T},\overrightarrow {p},\overrightarrow {b},X$ can easily be deduced from the solutions of the following two by two linear differential system:

$$ \frac{dY(s)}{ds}=\frac{i}{2}\begin{pmatrix} \kappa (s)& \tau(s)\\ -\tau(s)&-\kappa (s) \end{pmatrix} Y(s) $$

(122)

In fact, if $Y(s)$ is a resolvent matrix of this system, and if we introduce the imaginary Pauli matrices

$$ e_{1}{} ={}i\sigma_{1}{}={} \begin{pmatrix} 0& i\\ i&0 \end{pmatrix}\; e_{2}{}=i\sigma_{2}{}={} \begin{pmatrix} 0& 1\\ -1&0 \end{pmatrix}\; e_{3}{}=i\sigma_{3}{}={}\begin{pmatrix} i& 0\\ 0&-i \end{pmatrix} $$

(123)

satisfying

$$ e_{1}e_{2}-e_{2}e_{1}=-2e_{3},\; e_{2}e_{3}-e_{3}e_{2}=-2e_{1},\; e_{3}e_{1}-e_{1}e_{3}=-2e_{2}, $$

(124)

then the matrices

$$ \frac{1}{2}Ye_{1}Y^{-1}, \quad \frac{1}{2}Ye_{2}Y^{-1}, \quad\frac{1}{2}Ye_{3}Y^{-1}, $$

(125)

decomposed in the basis $e_{1},e_{2},e_{3}$ give respectively the vectorial functions $\overrightarrow {T}(s),\overrightarrow {p}(s),\overrightarrow {b}(s)$. Then the curve $X(s)$ can be deduced by one quadrature.

However there is no known explicit formula for $Y(s)$ when $\kappa$ and $\tau$ correspond to the particular curvature function $C(s)$ we found before. We can only compute their Taylor polynomials.