1 Introduction

The recognition of chaotic phenomena with hidden oscillations and self-excitations obeys the deterministic laws through which one can portray nonrandom chaos with unpredictable courses of events. Phenomena with hidden oscillations and self-excitation have had an enormous impact on all sciences and on popular culture as well. In exaggeration, actual dynamics are generally more regular than chaotic, which is because chaos sometimes necessitates parameters that are far superior to those we encounter in reality [1,2,3]. Leonov and Kuznetsov [4] categorized attractors in terms of new self-excited attractors and hidden attractors. They established a connection between the concept of hidden oscillations with some fundamental noted problems. These attractors were investigated by numerical methods from chaotic systems via modern computing software. Abro and Atangana [5] presented the different attractors of a drilling system based on an induction motor by means of newly presented fractal–fractional operators. Numerical simulations for the obtained solution were based on fractional techniques, and the results were discussed separately for fractional, fractal and fractal–fractional differential and integral operators. Leonov et al. [6] studied the convective flow of rotating fluid that is described by a system similar to the Lorenz-chaotic system, in which they emphasized that this system has a self-excited attractor with a homoclinic trajectory. They also found that if the physical model is purely Lorenz system then a hidden attractor can be localized. Akgul and Pehlivan [7] introduced a new chaotic system with no equilibrium point and dynamically analyzed the system by means of equilibrium points. They observed that this new system possessed fractal dimensions, chaotic behavior and sensitivity to initial conditions. Recent works on chaotic systems with no equilibrium points [8,9,10,11] and with equilibrium points can be found in [12,13,14,15].

In order to present the complex dynamical model, the following paragraphs explore the chaotic attractors via classical differentiation, fractional differentiation, fractal differentiation and fractal–fractional differentiation. Abro [16] presented an aerodynamic analysis of a wind turbine based on four different mathematical models depending on classical differentiation, fractional differentiation, fractal differentiation and fractal–fractional differentiation. The chaotic attractors and oscillations were obtained numerically and compared with different operators. Wang et al. [17] proposed a new three-dimensional chaotic system having no equilibrium point and hidden attractor with coexisting limit cycle. Dynamic analysis for the proposed no-equilibrium chaotic system has been observed in detail. The authors proposed application based on practical signal encryption and illustrated it numerically. Abro and Atangana [18] investigated a chaotic system with perpendicular line equilibrium, line equilibrium and without equilibrium by means of a fractal differential operator having a non-singular kernel. The simulations for dynamical systems have been depicted for periodicity and quasi-periodicity for chaos and hyperchaos. Yuan et al. [19] studied the chaotic oscillation of a model designed by meminductor and memcapacitor. They analyzed the five-dimensional chaotic oscillator for the considered model and reduced its chaotic complexity by reducing its dimensions to a three-dimensional system. Abro and Atangana [20] presented a fractal–fractionalized mathematical model for an electromechanical system consisting of motor and roller by three different techniques based on non-singularity and non-locality. Stability and effectiveness analysis were also carried out for all three models and compared. For the sake of simplicity in this manuscript, we focus on recent investigations related to chaotic attractors for transient anomalous diffusion [21], heat flow equation [22], longitudinal fin [23], piecewise differentials [24], fractional-order systems [25], resistance and conductance during magnetization [26], hyperchaos with synchronization [27], Shinriki’s oscillator model [28], free convective flow in a circular pipe [29], the Vallis model [30], nanofluid [31], a Chua attractor [32], non-Fourier heat conduction [33], and a two-wing smooth chaotic system [34].

Motivated by the above discussions, the fractal–fractionalized [35,36,37,38,39,40] chaotic chameleon system is developed to demonstrate random chaos and strange attractors. The mathematical modeling of the chaotic chameleon system is established through the Caputo–Fabrizio fractal–fractional differential operator versus the Atangana–Baleanu fractal–fractional differential operator. The fractal–fractional differential operators have suggested random chaos and strange attractors with hidden oscillations and self-excitation. The limiting cases of fractal–fractional differential operators have been invoked on the chaotic chameleon system, namely (i) variation of fractal domain by fixing fractional domain, (ii) variation of fractional domain by fixing fractal domain, and (iii) variation of the fractal domain as well as the fractional domain. Finally, the comparative analysis of the chaotic chameleon system based on singularity versus non-singularity and locality versus non-locality is depicted in terms of chaotic illustrations.

2 Development of a circuit based on the chaotic chameleon system

Although the dynamical properties from several novel chaotic systems can be achieved, we propose a circuit based on a chaotic chameleon system modeled via new fractal–fractional differential operators that has hidden oscillations and self-excitation based on the value of parameters \(({\rho }_{0},{\rho }_{1},{\rho }_{2})\) involved in it [41]. This circuit is fractal–fractionalized as:

$$\begin{aligned}{\mathfrak{D}}_{t}^{{\Upsilon }_{1}, {\Upsilon }_{2}}{\Lambda }_{1}\left(t\right)&={\rho }_{1}+{\Lambda }_{2}(t), \\{\mathfrak{D}}_{t}^{{\Upsilon }_{1}, {\Upsilon }_{2}}{\Lambda }_{2}\left(t\right)&=4{\Lambda }_{2}\left(t\right){\Lambda }_{3}\left(t\right)-7{\Lambda }_{1}\left(t\right), \\ {\mathfrak{D}}_{t}^{{\Upsilon }_{1}, {\Upsilon }_{2}}{\Lambda }_{3}\left(t\right)&={\rho }_{0}-{\left({\Lambda }_{1}\left(t\right)\right)}^{2}-{\left({\Lambda }_{2}\left(t\right)\right)}^{2}+{\rho }_{2} {\Lambda }_{3}\left(t\right)\end{aligned},$$
(1)

Here, \({\mathfrak{D}}_{t}^{{\Upsilon }_{1}, {\Upsilon }_{2}}\) is the Caputo–Fabrizio fractal–fractional differential operator, defined as [36]:

$${\mathfrak{D}}_{t}^{{\Upsilon }_{1}, {\Upsilon }_{2}}\Lambda \left(t\right)=M\left({\Upsilon }_{1}\right){\left(1-{\Upsilon }_{1}\right)}^{-1}\frac{\text{d}}{\text{d}{s}^{{\Upsilon }_{2}}}\underset{0}{\overset{t}{\int }}{\text{exp}}\left\{\frac{-{\Upsilon }_{1}\left(t-s\right)}{1-{\Upsilon }_{1}}\right\}\Lambda \left(s\right) \mathrm{d}s.$$
(2)

Here, \(M\left({\Upsilon }_{1}\right)\) is the normalization function of the Caputo–Fabrizio fractal–fractional differential operator, which is \(M\left({\Upsilon }_{1}\right)=M\left(0\right)=M\left(1\right)=1\). The circuit based on the chaotic chameleon system in terms of the Atangana–Baleanu fractal–fractionalized differential operator is defined as:

$$\begin{aligned}{\mathfrak{D}}_{t}^{{\Upsilon }_{3}, {\Upsilon }_{4}}{\Lambda }_{1}\left(t\right)&={\rho }_{1}+{\Lambda }_{2}(t), \\ {\mathfrak{D}}_{t}^{{\Upsilon }_{3}, {\Upsilon }_{4}}{\Lambda }_{2}\left(t\right)&=4{\Lambda }_{2}\left(t\right){\Lambda }_{3}\left(t\right)-7{\Lambda }_{1}\left(t\right), \\ {\mathfrak{D}}_{t}^{{\Upsilon }_{3}, {\Upsilon }_{4}}{\Lambda }_{3}\left(t\right)&={\rho }_{0}-{\left({\Lambda }_{1}\left(t\right)\right)}^{2}-{\left({\Lambda }_{2}\left(t\right)\right)}^{2}+{\rho }_{2} {\Lambda }_{3}\left(t\right)\end{aligned},$$
(3)

Equation (3) is the Atangana–Baleanu fractal–fractional differential operator, defined as [42]:

$${\mathfrak{D}}_{t}^{{\Upsilon }_{3}, {\Upsilon }_{4}}\Lambda \left(t\right)={\text{AB}}\left({\Upsilon }_{3}\right){\left(1-{\Upsilon }_{3}\right)}^{-1}\frac{\text{d}}{\text{d}{s}^{{\Upsilon }_{4}}}\underset{0}{\overset{t}{\int }}{\mathbf{E}}_{{\Upsilon }_{3}}\left\{\frac{-{\Upsilon }_{3}{\left(t-s\right)}^{{\Upsilon }_{3}}}{1-{\Upsilon }_{3}}\right\}\Lambda \left(s\right) \mathrm{d}s.$$
(4)

Here, \({\text{AB}}\left({\Upsilon }_{3}\right)\) is the normalization function of the Atangana–Baleanu fractal–fractional differential operator, which is \({\text{AB}}\left({\Upsilon }_{3}\right)=M\left(0\right)=M\left(1\right)=1\). The significance of this circuit based on a chaotic chameleon system modeled via new fractal–fractional differential operators is (i) \({\rho }_{1}=0\), then hidden attractors are achieved from Eq. (1) or (3), and (ii) \({\rho }_{1}\ne 0\), then self-excited attractors are achieved from Eq. (1) or (4), and the imposed initial conditions of a circuit based on the chaotic chameleon system are taken as \([{\Lambda }_{1}\left(t\right)=0.1,{\Lambda }_{2}\left(t\right)=0.01, {\Lambda }_{3}\left(t\right)=0.01]\). In order to investigate the fractional and fractal effects of a circuit based on a chaotic chameleon system in Eqs. (1) and (4), the following fractal–fractional integral operators are invoked as illustrated below:

$${\mathcal{I}}_{t}^{{\Upsilon }_{1},{\Upsilon }_{2}}\Lambda \left(t\right)=M\left({\Upsilon }_{1}\right)\underset{0}{\overset{t}{\int }}{\Upsilon }_{1}{\Upsilon }_{2}\Lambda \left(s\right){s}^{{\Upsilon }_{1}-1}\mathrm{d}s+\frac{\Lambda \left(t\right){s}^{{\Upsilon }_{2}-1}\left(1-{\Upsilon }_{1}\right){\Upsilon }_{1}}{M\left({\Upsilon }_{1}\right)}.$$
(5)
$${\mathcal{I}}_{t}^{{\Upsilon }_{3},{\Upsilon }_{4}}\Lambda \left(t\right)=\frac{1}{\text{AB}\left({\Upsilon }_{3}\right)}\underset{0}{\overset{t}{\int }}{\Upsilon }_{3}{\Upsilon }_{4}{\left(t-s\right)}^{{\Upsilon }_{3}-1}{s}^{{\Upsilon }_{4}-1}\Lambda \left(s\right)\mathrm{d}s+\frac{\Lambda \left(t\right){s}^{{\Upsilon }_{4}-1}(1-{\Upsilon }_{3}){\Upsilon }_{3}}{\text{AB}({\Upsilon }_{3})}.$$
(6)

Equations (5, 6) are the Caputo–Fabrizio and Atangana–Baleanu fractal–fractional integral operators [42], respectively.

3 Numerical treatment of a circuit based on a chaotic chameleon system

We discuss here two types of numerical schemes, the so-called Caputo–Fabrizio and Atangana–Baleanu fractal–fractional numerical schemes, based on the Adams–Bashforth–Moulton method, or multi-step integration method.

3.1 Numerical treatment via the Caputo–Fabrizio operator

Setting Eq. (1) for the Caputo–Fabrizio differential operator along with setting parameters as \({\mathfrak{R}}_{0}-{\mathfrak{R}}_{3}\), we arrive at:

$$\begin{array}{c}{\mathfrak{D}}_{t}^{{\Upsilon }_{1}, {\Upsilon }_{2}}{\Lambda }_{1}\left(t\right)-{t}^{{\Upsilon }_{1}-1}{w}_{1}\left({\mathfrak{R}}_{0}\right){\Upsilon }_{1}=0\\ \begin{array}{c}{\mathfrak{D}}_{t}^{{\Upsilon }_{1}, {\Upsilon }_{2}}{\Lambda }_{2}\left(t\right)-{t}^{{\Upsilon }_{1}-1}{w}_{2}\left({\mathfrak{R}}_{0}\right){\Upsilon }_{1}=0,\\ {\mathfrak{D}}_{t}^{{\Upsilon }_{1}, {\Upsilon }_{2}}{\Lambda }_{3}\left(t\right)-{t}^{{\Upsilon }_{1}-1}{w}_{3}\left({\mathfrak{R}}_{0}\right){\Upsilon }_{1}=0\end{array}\end{array}$$
(7)

Applying Eq. (5) on Eq. (7), we have

$$\begin{array}{c}{\Lambda }_{1}\left(t\right)={\Lambda }_{1}(0)+\frac{{\Upsilon }_{2}{t}^{{\Upsilon }_{2}-1}\left(1-{\Upsilon }_{1}\right)}{M\left({\Upsilon }_{1}\right)}{w}_{1}\left({\mathfrak{R}}_{0}\right)+\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\underset{0}{\overset{t}{\int }}{\Delta }^{{\Upsilon }_{2}-1}{w}_{1}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \\ \begin{array}{c}{\Lambda }_{2}\left(t\right)={\Lambda }_{2}(0)+\frac{{\Upsilon }_{2}{t}^{{\Upsilon }_{2}-1}\left(1-{\Upsilon }_{1}\right)}{M\left({\Upsilon }_{1}\right)}{w}_{2}\left({\mathfrak{R}}_{0}\right)+\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\underset{0}{\overset{t}{\int }}{\Delta }^{{\Upsilon }_{2}-1}{w}_{2}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \\ {\Lambda }_{3}\left(t\right)={\Lambda }_{3}(0)+\frac{{\Upsilon }_{2}{t}^{{\Upsilon }_{2}-1}\left(1-{\Upsilon }_{1}\right)}{M\left({\Upsilon }_{1}\right)}{w}_{3}\left({\mathfrak{R}}_{0}\right)+\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\underset{0}{\overset{t}{\int }}{\Delta }^{{\Upsilon }_{2}-1}{w}_{3}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \end{array}\end{array}$$
(8)

Equation (8) is expanded at \({t}_{{\varOmega }_{1}+1}\) as

$$\begin{array}{c}{{\Lambda }_{1}}_{{\varOmega }_{1}+1}\left(t\right)={{\Lambda }_{1}}_{0}+\frac{{\Upsilon }_{2}\left(1-{\Upsilon }_{1}\right)}{{t}_{{\varOmega }_{1}}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}{w}_{1}\left({\mathfrak{R}}_{2}\right)+\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\underset{0}{\overset{{t}_{{\varOmega }_{1}+1}}{\int }}{\Delta }^{{\Upsilon }_{2}-1}{w}_{1}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \\ \begin{array}{c}{{\Lambda }_{2}}_{{\varOmega }_{1}+1}\left(t\right)={{\Lambda }_{2}}_{0}+\frac{{\Upsilon }_{2}\left(1-{\Upsilon }_{1}\right)}{{t}_{{\varOmega }_{1}}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}{w}_{2}\left({\mathfrak{R}}_{2}\right)+\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\underset{0}{\overset{{t}_{{\varOmega }_{1}+1}}{\int }}{\Delta }^{{\Upsilon }_{2}-1}{w}_{2}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \\ {{\Lambda }_{3}}_{{\varOmega }_{1}+1}\left(t\right)={{\Lambda }_{3}}_{0}+\frac{{\Upsilon }_{2}\left(1-{\Upsilon }_{1}\right)}{{t}_{{\varOmega }_{1}}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}{w}_{3}\left({\mathfrak{R}}_{2}\right)+\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\underset{0}{\overset{{t}_{{\varOmega }_{1}+1}}{\int }}{\Delta }^{{\Upsilon }_{2}-1}{w}_{3}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \end{array}\end{array}$$
(9)

Taking the difference between the consecutive terms of Eq. (9) as

$$\begin{array}{c}\begin{array}{c}{{\Lambda }_{1}}_{{\varOmega }_{1}+1}\left(t\right)={{\Lambda }_{1}}_{{\varOmega }_{1}}+\frac{{\Upsilon }_{2}\left(1-{\Upsilon }_{1}\right)}{{t}_{{\varOmega }_{1}}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}{w}_{1}\left({\mathfrak{R}}_{2}\right)-\frac{{\Upsilon }_{2}{t}_{{\varOmega }_{1}-1}^{{\Upsilon }_{2}-1}\left(1-{\Upsilon }_{1}\right)}{M\left({\Upsilon }_{1}\right)}\\ \quad \times {w}_{1}\left({\mathfrak{R}}_{3}\right)+\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\underset{{t}_{{\varOmega }_{1}}}{\overset{{t}_{{\varOmega }_{1}+1}}{\int }}{\lambda }^{{\Upsilon }_{2}-1}{w}_{1}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta },\end{array}\\ \begin{array}{c}\begin{array}{c}{{\Lambda }_{2}}_{{\varOmega }_{1}+1}\left(t\right)={{\Lambda }_{2}}_{{\varOmega }_{1}}+\frac{{\Upsilon }_{2}\left(1-{\Upsilon }_{1}\right)}{{t}_{{\varOmega }_{1}}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}{w}_{2}\left({\mathfrak{R}}_{2}\right)-\frac{{\Upsilon }_{2}{t}_{{\varOmega }_{1}-1}^{{\Upsilon }_{2}-1}\left(1-{\Upsilon }_{1}\right)}{M\left({\Upsilon }_{1}\right)}\\\quad {\times w}_{2}\left({\mathfrak{R}}_{3}\right)+\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\underset{{t}_{{\varOmega }_{1}}}{\overset{{t}_{{\varOmega }_{1}+1}}{\int }}{\lambda }^{{\Upsilon }_{2}-1}{w}_{2}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta },\end{array}\\ \begin{array}{c}{{\Lambda }_{3}}_{{\varOmega }_{1}+1}\left(t\right)={{\Lambda }_{3}}_{{\varOmega }_{1}}+\frac{{\Upsilon }_{2}\left(1-{\Upsilon }_{1}\right)}{{t}_{{\varOmega }_{1}}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}{w}_{3}\left({\mathfrak{R}}_{2}\right)-\frac{{\Upsilon }_{2}{t}_{{\varOmega }_{1}-1}^{{\Upsilon }_{2}-1}\left(1-{\Upsilon }_{1}\right)}{M\left({\Upsilon }_{1}\right)}\\ \quad{\times w}_{3}\left({\mathfrak{R}}_{3}\right)+\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\underset{{t}_{{\varOmega }_{1}}}{\overset{{t}_{{\varOmega }_{1}+1}}{\int }}{\lambda }^{{\Upsilon }_{2}-1}{w}_{3}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta },\end{array}\end{array}\end{array}$$
(10)

Solving integration and the Lagrange polynomial piecewise interpolation of Eq. (10), the result is:

$$\begin{aligned}{{\Lambda }_{1}}_{{\varOmega }_{1}+1}\left(t\right)&={{\Lambda }_{1}}_{{\varOmega }_{1}}+\left(\frac{{w}_{1}\left({\mathfrak{R}}_{2}\right)}{{t}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}-\frac{{w}_{1}\left({\mathfrak{R}}_{3}\right)}{{t}_{{\varOmega }_{1}-1}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}\right){\Upsilon }_{2}\left(1-{\Upsilon }_{1}\right)\\ &\quad+\frac{h}{2}\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\left\{\frac{3}{{t}_{{\varOmega }_{1}}^{{1-\Upsilon }_{2}}}{w}_{1}\left({\mathfrak{R}}_{2}\right)-{t}_{{\varOmega }_{1}-1}^{{\Upsilon }_{2}-1}{w}_{1}\left({\mathfrak{R}}_{3}\right)\right\},\\ {{\Lambda }_{2}}_{{\varOmega }_{1}+1}\left(t\right)&={{\Lambda }_{2}}_{{\varOmega }_{1}}+\left(\frac{{w}_{2}\left({\mathfrak{R}}_{2}\right)}{{t}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}-\frac{{w}_{2}\left({\mathfrak{R}}_{3}\right)}{{t}_{{\varOmega }_{1}-1}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}\right){\Upsilon }_{2}\left(1-{\Upsilon }_{1}\right)\\&\quad +\frac{h}{2}\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\left\{\frac{3}{{t}_{{\varOmega }_{1}}^{{1-\Upsilon }_{2}}}{w}_{2}\left({\mathfrak{R}}_{2}\right)-{t}_{{\varOmega }_{1}-1}^{{\Upsilon }_{2}-1}{w}_{2}\left({\mathfrak{R}}_{3}\right)\right\}, \\ {{\Lambda }_{3}}_{{\varOmega }_{1}+1}\left(t\right)&={{\Lambda }_{3}}_{{\varOmega }_{1}}+\left(\frac{{w}_{3}\left({\mathfrak{R}}_{2}\right)}{{t}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}-\frac{{w}_{3}\left({\mathfrak{R}}_{3}\right)}{{t}_{{\varOmega }_{1}-1}^{1-{\Upsilon }_{2}}M\left({\Upsilon }_{1}\right)}\right){\Upsilon }_{2}\left(1-{\Upsilon }_{1}\right)\\&\quad +\frac{h}{2}\frac{{\Upsilon }_{1}{\Upsilon }_{2}}{M\left({\Upsilon }_{1}\right)}\left\{\frac{3}{{t}_{{\varOmega }_{1}}^{{1-\Upsilon }_{2}}}{w}_{3}\left({\mathfrak{R}}_{2}\right)-{t}_{{\varOmega }_{1}-1}^{{\Upsilon }_{2}-1}{w}_{3}\left({\mathfrak{R}}_{3}\right)\right\}, \end{aligned},$$
(11)

Calculating Eq. (11), the resultant numerical scheme is for the Caputo–Fabrizio fractal–fractional operator is

$$\begin{aligned}{{\Lambda }_{1}}_{{\varOmega }_{1}+1}\left(t\right)&={{\Lambda }_{1}}_{{\varOmega }_{1}}+{\Upsilon }_{2}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{2}-1}\left(\frac{1-{\Upsilon }_{1}}{M({\Upsilon }_{1})}+\frac{3{\Upsilon }_{1}h}{2M({\Upsilon }_{1})}\right){w}_{1}\left({\mathfrak{R}}_{2}\right)-{\Upsilon }_{2}{t}_{{\varOmega }_{1}-1}^{{\Upsilon }_{2}-1}\\ &\quad\times \left(\frac{1-{\Upsilon }_{1}}{M\left({\Upsilon }_{1}\right)}+\frac{{\Upsilon }_{1}h}{2M\left({\Upsilon }_{1}\right)}\right){w}_{1}\left({\mathfrak{R}}_{3}\right), \\{{\Lambda }_{2}}_{{\varOmega }_{1}+1}\left(t\right)&={{\Lambda }_{2}}_{{\varOmega }_{1}}+{\Upsilon }_{2}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{2}-1}\left(\frac{1-{\Upsilon }_{1}}{M({\Upsilon }_{1})}+\frac{3{\Upsilon }_{1}h}{2M({\Upsilon }_{1})}\right){w}_{2}\left({\mathfrak{R}}_{2}\right)-{\Upsilon }_{2}{t}_{{\varOmega }_{1}-1}^{{\Upsilon }_{2}-1}\\ &\quad \times \left(\frac{1-{\Upsilon }_{1}}{M\left({\Upsilon }_{1}\right)}+\frac{{\Upsilon }_{1}h}{2M\left({\Upsilon }_{1}\right)}\right){w}_{2}\left({\mathfrak{R}}_{3}\right), \\ {{\Lambda }_{3}}_{{\varOmega }_{1}+1}\left(t\right)&={{\Lambda }_{3}}_{{\varOmega }_{1}}+{\Upsilon }_{2}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{2}-1}\left(\frac{1-{\Upsilon }_{1}}{M({\Upsilon }_{1})}+\frac{3{\Upsilon }_{1}h}{2M({\Upsilon }_{1})}\right){w}_{3}\left({\mathfrak{R}}_{2}\right)-{\Upsilon }_{2}{t}_{{\varOmega }_{1}-1}^{{\Upsilon }_{2}-1}\\ &\quad\times \left(\frac{1-{\Upsilon }_{1}}{M\left({\Upsilon }_{1}\right)}+\frac{{\Upsilon }_{1}h}{2M\left({\Upsilon }_{1}\right)}\right){w}_{3}\left({\mathfrak{R}}_{3}\right), \end{aligned}.$$
(12)

3.2 Numerical treatment via the Atangana–Baleanu operator

Setting Eq. (3) for the Atangana–Baleanu differential operator along with setting parameters as \({\mathfrak{R}}_{0}-{\mathfrak{R}}_{3}\), we arrive at:

$$\begin{array}{c}{\mathfrak{D}}_{t}^{{\Upsilon }_{3}, {\Upsilon }_{4}}{\Lambda }_{1}\left(t\right)-{t}^{{\Upsilon }_{3}-1}{w}_{1}\left({\mathfrak{R}}_{0}\right){\Upsilon }_{3}=0\\ \begin{array}{c}{\mathfrak{D}}_{t}^{{\Upsilon }_{3}, {\Upsilon }_{4}}{\Lambda }_{2}\left(t\right)-{t}^{{\Upsilon }_{3}-1}{w}_{2}\left({\mathfrak{R}}_{0}\right){\Upsilon }_{3}=0,\\ {\mathfrak{D}}_{t}^{{\Upsilon }_{3}, {\Upsilon }_{4}}{\Lambda }_{3}\left(t\right)-{t}^{{\Upsilon }_{3}-1}{w}_{3}\left({\mathfrak{R}}_{0}\right){\Upsilon }_{3}=0\end{array}\end{array}$$
(13)

Applying Eq. (6) on Eq. (13), we have

$$\begin{array}{c}{\Lambda }_{1}\left(t\right)={\Lambda }_{1}(0)+\frac{{\Upsilon }_{4}{t}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right){w}_{1}\left({\mathfrak{R}}_{0}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}+\frac{{\Upsilon }_{3}{\Upsilon }_{4}{\Delta }^{{\Upsilon }_{4}-1}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}\right)}\underset{0}{\overset{t}{\int }}{(t-\Delta )}^{{\Upsilon }_{3}-1}{w}_{1}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \\ \begin{array}{c}{\Lambda }_{2}\left(t\right)={\Lambda }_{2}(0)+\frac{{\Upsilon }_{4}{t}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right){w}_{2}\left({\mathfrak{R}}_{0}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}+\frac{{\Upsilon }_{3}{\Upsilon }_{4}{\Delta }^{{\Upsilon }_{4}-1}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}\right)}\underset{0}{\overset{t}{\int }}{(t-\Delta )}^{{\Upsilon }_{3}-1}{w}_{2}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \\ {\Lambda }_{3}\left(t\right)={\Lambda }_{3}(0)+\frac{{\Upsilon }_{4}{t}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right){w}_{3}\left({\mathfrak{R}}_{0}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}+\frac{{\Upsilon }_{3}{\Upsilon }_{4}{\Delta }^{{\Upsilon }_{4}-1}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}\right)}\underset{0}{\overset{t}{\int }}{(t-\Delta )}^{{\Upsilon }_{3}-1}{w}_{3}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta },\end{array}\end{array}$$
(14)

Equation (14) is expanded at \({t}_{{\varOmega }_{1}+1}\) as

$$\begin{aligned}{{\Lambda }_{1}}_{{\varOmega }_{1}+1}&={{\Lambda }_{1}}_{0}+\frac{{\Upsilon }_{4}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}{w}_{1}\left({\mathfrak{R}}_{2}\right)+\frac{{\Upsilon }_{3}{\Upsilon }_{4}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}\right)}\underset{0}{\overset{{t}_{{\varOmega }_{1}+1} }{\int }}{\Delta }^{{\Upsilon }_{4}-1}\\ &\quad \times {\left({t}_{{\varOmega }_{1}+1} -\Lambda \right)}^{{\Upsilon }_{3}-1}{w}_{1}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta },\\ {{\Lambda }_{2}}_{{\varOmega }_{1}+1}&={{\Lambda }_{2}}_{0}+\frac{{\Upsilon }_{4}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}{w}_{2}\left({\mathfrak{R}}_{2}\right)+\frac{{\Upsilon }_{3}{\Upsilon }_{4}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}\right)}\underset{0}{\overset{{t}_{{\varOmega }_{1}+1} }{\int }}{\Delta }^{{\Upsilon }_{4}-1}\\ &\quad \times {\left({t}_{{\varOmega }_{1}+1} -\Delta \right)}^{{\Upsilon }_{3}-1}{w}_{2}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta },\\{{\Lambda }_{3}}_{{\varOmega }_{1}+1}&={{\Lambda }_{3}}_{0}+\frac{{\Upsilon }_{4}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}{w}_{3}\left({\mathfrak{R}}_{2}\right)+\frac{{\Upsilon }_{3}{\Upsilon }_{4}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}\right)}\underset{0}{\overset{{t}_{{\varOmega }_{1}+1} }{\int }}{\Delta }^{{\Upsilon }_{4}-1}\\ &\quad \times {\left({t}_{{\varOmega }_{1}+1} -\Delta \right)}^{{\Upsilon }_{3}-1}{w}_{3}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \end{aligned} ,$$
(15)

The simplified form of Eq. (15) within the interval \(\left[{t}_{{\varOmega }_{2}},{t}_{{\varOmega }_{2}+1}\right]\) is calculated as:

$$\begin{aligned}{{\Lambda }_{1}}_{{\varOmega }_{1}+1}&={{\Lambda }_{1}}_{0}+\frac{{\Upsilon }_{4}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right){w}_{1}\left({\mathfrak{R}}_{2}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}+\frac{{\Upsilon }_{3}{\Upsilon }_{4}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}\right)}\sum_{{\varOmega }_{2}=0}^{{\varOmega }_{1}}\underset{{t}_{{\varOmega }_{2}}}{\overset{{t}_{{\varOmega }_{2}+1}}{\int }}{\Delta }^{{\Upsilon }_{4}-1}\\ &\quad\times {\left({t}_{{\varOmega }_{1}+1}-\Delta \right)}^{{\Upsilon }_{3}-1}{w}_{1}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \\{{\Lambda }_{2}}_{{\varOmega }_{1}+1}&={{\Lambda }_{2}}_{0}+\frac{{\Upsilon }_{4}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right){w}_{2}\left({\mathfrak{R}}_{2}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}+\frac{{\Upsilon }_{3}{\Upsilon }_{4}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}\right)}\sum_{{\varOmega }_{2}=0}^{{\varOmega }_{1}}\underset{{t}_{{\varOmega }_{2}}}{\overset{{t}_{{\varOmega }_{2}+1}}{\int }}{\Delta }^{{\Upsilon }_{4}-1}\\ &\quad \times {\left({t}_{{\varOmega }_{1}+1}-\Delta \right)}^{{\Upsilon }_{3}-1}{w}_{2}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \\{{\Lambda }_{3}}_{{\varOmega }_{1}+1}&={{\Lambda }_{3}}_{0}+\frac{{\Upsilon }_{4}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right){w}_{3}\left({\mathfrak{R}}_{2}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}+\frac{{\Upsilon }_{3}{\Upsilon }_{4}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}\right)}\sum_{{\varOmega }_{2}=0}^{{\varOmega }_{1}}\underset{{t}_{{\varOmega }_{2}}}{\overset{{t}_{{\varOmega }_{2}+1}}{\int }}{\Delta }^{{\Upsilon }_{4}-1}\\ &\quad \times {\left({t}_{{\varOmega }_{1}+1}-\Delta \right)}^{{\Upsilon }_{3}-1}{w}_{3}\left({\mathfrak{R}}_{1}\right)\mathrm{d\Delta }, \end{aligned} ,$$
(16)

Calculating Eq. (16), the numerical scheme for the Atangana–Baleanu fractal–fractional operator is

$$\begin{array}{c}\begin{array}{c}\begin{array}{c}{{\Lambda }_{1}}_{{\varOmega }_{1}+1}={{\Lambda }_{1}}_{0}+\frac{{\Upsilon }_{4}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right){w}_{1}\left({\mathfrak{R}}_{2}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}+\frac{{\left({\Upsilon }_{4}t\right)}^{{\Upsilon }_{3}}{\Upsilon }_{4}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}+2\right)}\sum_{{\varOmega }_{2}=0}^{{\varOmega }_{1}}\left[{t}_{{\varOmega }_{2}}^{{\Upsilon }_{4}-1}\right. \\ \times {w}_{1}\left({\mathfrak{R}}_{2}\right)\left\{{\left({\varOmega }_{1}+1-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}}\left({\varOmega }_{1}-{\varOmega }_{2}+2+{\Upsilon }_{5}\right)-{\left({\varOmega }_{1}-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}}\left({\varOmega }_{1}-{\varOmega }_{2}+2+2{\Upsilon }_{5}\right)\right\}\end{array}\\ \left.-{t}_{{\varOmega }_{2}-1}^{{\Upsilon }_{4}-1}{w}_{1}\left({\mathfrak{R}}_{3}\right){\left({\varOmega }_{1}+1-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}+1}-{\left({\varOmega }_{1}-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}}\left({\varOmega }_{1}-{\varOmega }_{2}+1+{\Upsilon }_{5}\right)\right], \end{array}\\ \begin{array}{c}\begin{array}{c}\begin{array}{c}{{\Lambda }_{2}}_{{\varOmega }_{1}+1}={{\Lambda }_{2}}_{0}+\frac{{\Upsilon }_{4}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right){w}_{2}\left({\mathfrak{R}}_{2}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}+\frac{{\left({\Upsilon }_{4}t\right)}^{{\Upsilon }_{3}}{\Upsilon }_{4}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}+2\right)}\sum_{{\varOmega }_{2}=0}^{{\varOmega }_{1}}\left[{t}_{{\varOmega }_{2}}^{{\Upsilon }_{4}-1}\right. \\ \times {w}_{2}\left({\mathfrak{R}}_{2}\right)\left\{{\left({\varOmega }_{1}+1-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}}\left({\varOmega }_{1}-{\varOmega }_{2}+2+{\Upsilon }_{5}\right)-{\left({\varOmega }_{1}-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}}\left({\varOmega }_{1}-{\varOmega }_{2}+2+2{\Upsilon }_{5}\right)\right\} \end{array}\\ -{t}_{{\varOmega }_{2}-1}^{{\Upsilon }_{4}-1}\left.{w}_{2}\left({\mathfrak{R}}_{3}\right){\left({\varOmega }_{1}+1-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}+1}-{\left({\varOmega }_{1}-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}}\left({\varOmega }_{1}-{\varOmega }_{2}+1+{\Upsilon }_{5}\right)\right], \end{array}\\ \begin{array}{c}\begin{array}{c}{{\Lambda }_{3}}_{{\varOmega }_{1}+1}={{\Lambda }_{3}}_{0}+\frac{{\Upsilon }_{4}{t}_{{\varOmega }_{1}}^{{\Upsilon }_{4}-1}\left(1-{\Upsilon }_{3}\right){w}_{3}\left({\mathfrak{R}}_{2}\right)}{\text{AB}\left({\Upsilon }_{3}\right)}+\frac{{\left({\Upsilon }_{4}t\right)}^{{\Upsilon }_{3}}{\Upsilon }_{4}}{\text{AB}\left({\Upsilon }_{3}\right)\Gamma \left({\Upsilon }_{3}+2\right)}\sum_{{\varOmega }_{2}=0}^{{\varOmega }_{1}}\left[{t}_{{\varOmega }_{2}}^{{\Upsilon }_{4}-1}\right. \\ \times {w}_{3}\left({\mathfrak{R}}_{2}\right)\left\{{\left({\varOmega }_{1}+1-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}}\left({\varOmega }_{1}-{\varOmega }_{2}+2+{\Upsilon }_{5}\right)-{\left({\varOmega }_{1}-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}}\left({\varOmega }_{1}-{\varOmega }_{2}+2+2{\Upsilon }_{5}\right)\right\}\end{array}\\ -{t}_{{\varOmega }_{2}-1}^{{\Upsilon }_{4}-1}\left.{w}_{3}\left({\mathfrak{R}}_{3}\right){\left({\varOmega }_{1}+1-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}+1}-{\left({\varOmega }_{1}-{\varOmega }_{2}\right)}^{{\Upsilon }_{3}}\left({\varOmega }_{1}-{\varOmega }_{2}+1+{\Upsilon }_{5}\right)\right], \end{array}\end{array}\end{array}.$$
(17)

4 Stability of the fractal–fractional chaotic chameleon system

A stable system is one in which a large change to the initial state produces a small change to a later state. In this regard, the chameleon chaotic system shows hidden and self-excited oscillations under the embedded parameters at specific values, which are presented in the Table 1.

Table 1 Hidden and self-excited attractors for the fractal–fractional chaotic chameleon system
Full size table

4.1 Equilibrium points

The equilibrium points of the fractal–fractional chameleon system can be found using the eigenvalues, employing Routh-Hurwitz stability analysis. The parameter \({\rho }_{1}\) plays a crucial role in defining the behavior of the fractal–fractional chameleon system. By considering the Jacobi matrix and \({\mathfrak{D}}_{t}^{{\Upsilon }_{1}, {\Upsilon }_{2}}{\Lambda }_{1}\left(t\right)={\mathfrak{D}}_{t}^{{\Upsilon }_{1}, {\Upsilon }_{2}}{\Lambda }_{2}\left(t\right)={\mathfrak{D}}_{t}^{{\Upsilon }_{1}, {\Upsilon }_{2}}{\Lambda }_{3}\left(t\right)=0\), the equilibrium points are

\({\Lambda }_{1}=\pm 12.25\sqrt{\left({\rho }_{0}-{\rho }_{1}^{2}\right)},{\Lambda }_{2}=-{\rho }_{1}\) and \({\Lambda }_{3}=\pm \frac{3.5}{2{\rho }_{1}}\sqrt{\left({\rho }_{0}-{\rho }_{1}^{2}\right)}\). The fractal–fractional chameleon system has an unstable equilibrium \({E}_{\mathrm{1,2}}=\pm 0.4,-0.8, \pm 0.8750\) if \({\Lambda }_{2}=0.8\). It is also observed that the fractal–fractional chameleon system has no equilibrium if \({\Lambda }_{2}=0\).

4.2 Lyapunov exponents and Kaplan–Yorke (KY) dimension

The Lyapunov exponent is a useful analytical metric that can help to characterize chaos in the fractal–fractional chameleon system based on the principal criteria of chaos, and it represents the rate of growth or decline. In a fractal–fractional chameleon system, the existence of a positive Lyapunov exponent confirms the chaotic behavior of the system. In order to detect chaos in the fractal–fractional chameleon system, Table 2 is prepared for the Lyapunov exponents and KY dimension of the fractal–fractional chameleon system.

Table 2 Lyapunov exponents and Kaplan–Yorke dimension for the fractal–fractional chameleon system
Full size table

5 Numerical simulations and discussion

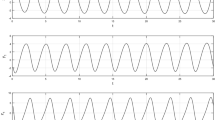
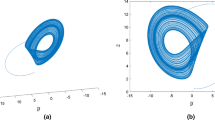
A circuit based on a chaotic chameleon system was modeled via new fractal–fractional differential operators, in which hidden oscillations and self-excitations were detected based on the value of parameters \(({\rho }_{0},{\rho }_{1},{\rho }_{2})\) involved. This circuit is fractal–fractionalized by imposing initial conditions taken as \(({\Lambda }_{1}\left(t\right)=0.1,{\Lambda }_{2}\left(t\right)=0.01, {\Lambda }_{3}\left(t\right)=0.01)\). This chaotic chameleon system has viewed two types of attractors: (i) self-excited attractor when \({\rho }_{1}\) is varied (not fixed at zero) and (ii) hidden attractor when \({\rho }_{1}\) is not varied (fixed at zero). Such qualitative attractors have been investigated for the first time in the open literature via new fractal–fractional differential operators. An electronic circuit based on the chaotic chameleon system generated chaotic attractors via variability of the fractional parameter and non-variability of the fractal parameter of the Caputo–Fabrizio operator in Fig. 1. Here, 2-D and 3-D phase images of the self-excited and hidden oscillations with the new Caputo–Fabrizio fractal–fractional differential operator are investigated.

Fig. 1
figure 1

Chaotic attractors via variability of fractional parameter and non-variability of the fractal parameter of the Caputo–Fabrizio operator with initial conditions taken as \(({\Lambda }_{1}\left(t\right)=0.1,{\Lambda }_{2}\left(t\right)=0.01, {\Lambda }_{3}\left(t\right)=0.01)\)

Full size image

Figure 2 presents 2-D and 3-D phase images of the self-excited and hidden oscillations with the new Atangana–Baleanu fractal–fractional differential operator. Here, the electronic circuit based on the chaotic chameleon system generated chaotic attractors via variability of the fractional parameter, and the non-variability of the fractal parameter generated significant attractors. In order to assess the memory effects of the newly defined fractal–fractional differential Caputo–Fabrizio operator, Fig. 3 presents the chaotic attractors via non-variability of the fractional parameter and variability of the fractal parameter of the Caputo–Fabrizio operator from the chameleon system. Whereas the Caputo–Fabrizio fractal–fractional differential operator is non-singular with locality, the Atangana–Baleanu fractal–fractional differential operator is non-singular with non-locality. In order to compare the results of the fractal–fractional differential operators for capturing memory effects, we present Fig. 4 for the chaotic chameleon system for the sake of non-variability of the fractional parameter and variability of the fractal parameter through the Atangana–Baleanu operator. Additionally, the combined effects of non-singular kernel and non-local kernel are presented in Fig. 5 for an electronic circuit based on the chaotic chameleon system generated chaotic attractors via variability of the fractional parameter as well as fractal parameters of the Atangana–Baleanu operator. The focus of this manuscript is to assess the fractional, classical and non-fractional systems with singularity versus non-singularity and locality versus non-locality effects on the memory of an electronic circuit based on a chaotic chameleon system. To the best of the author’s knowledge, this is the first interesting mathematical model of an electronic circuit based on a chaotic chameleon system that is studied through fractal–fractional differential operators with comparison. To conclude, self-excited attractors are investigated when \({\rho }_{0}<0\) and \({\rho }_{1}=0\), and if \({\rho }_{0}=0\) and \({\rho }_{1}\ne 0\), then no equilibrium point is observed. This is because the system (3) displays a routine period-doubling route to chaos and traces the state trajectories in the vicinity subject to both chaotic and dissipative processes.

Fig. 2
figure 2

Chaotic attractors via variability of the fractional parameter and non-variability of the fractal parameter of the Atangana–Baleanu operator with initial conditions taken as \(({\Lambda }_{1}\left(t\right)=0.1,{\Lambda }_{2}\left(t\right)=0.01, {\Lambda }_{3}\left(t\right)=0.01)\)

Full size image
Fig. 3
figure 3

Chaotic attractors via non-variability of the fractional parameter and variability of the fractal parameter of the Caputo–Fabrizio operator with initial conditions taken as \(({\Lambda }_{1}\left(t\right)=0.1,{\Lambda }_{2}\left(t\right)=0.01, {\Lambda }_{3}\left(t\right)=0.01)\)

Full size image
Fig. 4
figure 4

Chaotic attractors via non-variability of the fractional parameter and variability of the fractal parameter of the Atangana–Baleanu operator with initial conditions taken as \(({\Lambda }_{1}\left(t\right)=0.1,{\Lambda }_{2}\left(t\right)=0.01, {\Lambda }_{3}\left(t\right)=0.01)\)

Full size image
Fig. 5
figure 5

Chaotic attractors via variability of the fractional parameter as well as the fractal parameters of the Atangana–Baleanu operator with initial conditions taken as \(({\Lambda }_{1}\left(t\right)=0.1,{\Lambda }_{2}\left(t\right)=0.01, {\Lambda }_{3}\left(t\right)=0.01)\)

Full size image

6 Conclusion

A chameleon chaotic system is a chaotic system in which the chaotic attractor can change between a hidden and self-excited attractor depending on the values of parameters. In this regard, a fractal–fractionalized chaotic chameleon system is developed to demonstrate random chaos and strange attractors via mathematical modeling. The Caputo–Fabrizio fractal–fractional differential operator versus the Atangana–Baleanu fractal–fractional differential operator was simulated to display the random chaos and strange attractors with hidden oscillations and self-excitation. This investigation offers a simple algorithm for synthesizing one-parameter chameleon systems based on a new definition of differential operators known as the Caputo–Fabrizio fractal–fractional differential operator versus the Atangana–Baleanu fractal–fractional differential operator. The fractal–fractional-order chaotic chameleon system was shown to be asymmetric, dissimilar, and topologically nonequivalent to typical chaotic systems rectifying trajectories in vicinity and dissipative processes.