1 Introduction

The semiconductor industry is moving toward nanowire gate-all-around MOSFETs to improve the gate control [1,2,3]. Due to the small wire diameter, short gate lengths are feasible, but this does not mean that the transport is quasi-ballistic and scattering should be included in the simulations [4, 5]. Furthermore, transient simulations are required to determine the switching speed and RF performance of those devices. These types of simulations are very CPU intensive, when performed by quantum transport models (QTM) including scattering, and the drift-diffusion model (DDM) calibrated with results of a QTM is often used instead for device design (e.g., [5]). The DDM is not only by many orders of magnitude more CPU efficient than the QTMs, but also numerically very stable [6, 7]. Sophisticated algorithms exist to routinely obtain convergence of the nonlinear system of partial differential equations [8]. This is the reason, why the DDM is still the workhorse of today’s TCAD. On the other hand, it was pointed out quite early that the DDM suffers from stringent approximations and might fail in the case of quasi-ballistic transport [9]. The Boltzmann transport equation (BE) is a more physics-based (albeit more CPU intensive) semi-classical alternative, which can handle intricate band structures together with quasi-ballistic and diffusive transport [10, 11]. In the case of nanowires, the multi-subband BE is solved together with the 3D Poisson equation (PE) and Schrödinger equations (SE) for the cross sections [12, 13]. In this paper, we will show that the discrete BE can compete with the DDM w.r.t. numerical stability.

The BE is a partial differential equation with the possibility of discontinuous solutions, which can lead to numerical problems when it is mapped onto a grid in phase space. The most popular method to stabilize the BE for a 3D k-space is its expansion by spherical harmonics in the k-space and a transformation onto the total energy (H-transform) [14]. Only the lowest spherical harmonic is nonnegative, and by projection onto the spherical harmonics, it is no longer guaranteed that the distribution function is nonnegative [15]. This degrades the stability. However, by choosing a different set of functions that are nonnegative themselves for projection, this problem can be avoided [12, 13, 16,17,18,19,20]. Such functions are directly defined in the phase space and are piecewise constant with a value of either zero or one. The areas in which the functions are one do not overlap for different functions, which makes them orthogonal in this sense. Projection of the BE onto such functions is a prerequisite to preserve the nonnegativeness of the distribution function.

The simplest set of functions is given by a tessellation of the phase space into non-overlapping contiguous cells, where for each cell a function is defined that is one within the cell and zero outside of it. For the tessellated phase space, a discrete equivalent of the BE has to be found that conserves the nonnegativeness of the distribution function and that is numerically stable. If we neglect scattering, the BE reduces to the Liouville equation, which describes particle flux conservation in the phase space. Exact flux conservation in the phase space is possible by discretizing the Liouville equation with the finite volume method (FVM), where the cells of the tessellated phase space are the finite volumes [21]. Thus, fundamental conservation laws (e.g., charge conservation) are satisfied by construction of the discrete BE, if the scattering integral is discretized accordingly.

The calculation of the fluxes on the surfaces of the finite volumes has a strong impact on the numerical stability. Since the motion of particles is similar to waves in fluids, we use methods developed for computational fluid dynamics, which can handle, for example, discontinuous distribution functions [21]. Such an approach was presented in Ref. [22] based on Godunov’s scheme [23]. As pointed out in Ref. [24], the finite volumes should be aligned with lines of constant total energy (H-transform) to avoid spurious diffusion in the k-space. It should be mentioned that the H-transform comes at the price of additional derivatives w.r.t. time in the discrete BE, because in the transient case the phase space grid depends on time [25]. This again leads to spurious diffusion in the k-space as shown below, whereas a phase space grid fixed in time does not have this problem. Thus, in the transient case, spurious diffusion in the k-space cannot be completely suppressed by the H-transform.

In this work, we discuss the numerical properties of this approach, which is not limited to the 1D k-space of nanowires, but can also be applied in the case of a 2D or 3D k-space. The approach can handle complex band structures as they occur, for example, in the case of PMOSFETs [26, 27]. The nonlinear scattering integral including the Pauli principle is discretized in such a way that it conserves the particle number and satisfies the principle of detailed balance at equilibrium. We will show that the discrete BE yields nonnegative solutions by construction and that the corresponding system matrix is diagonally dominant resulting in excellent numerical stability. Due to its stability, the discrete BE can be integrated in time by the CPU-efficient forward Euler scheme. The numerical properties of the simulation approach are demonstrated for a silicon nanowire NMOSFET under stationary and transient conditions. Furthermore, we discuss the problems of the spurious damping and asymmetry introduced by Godunov’s scheme.

2 Simulation model

In the following, the time argument t is not shown to reduce the length of the formulas. It is implicitly understood that all solution variables, quantities derived from them and applied voltages can depend on time.

2.1 Subband structure

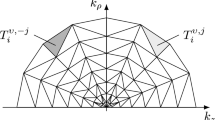
In the case of a nanowire MOSFET, we solve the PE, SE and BE self-consistently as explained in Refs. [12, 20]. The quasi-stationary SE yields the subband structure with the total energy \(\varepsilon ^{\text {tot}}_{\upsilon }(z,k)\) of the \(\upsilon\)th subband and the wave function \(\Psi _{\upsilon }(x,y;z,k)\) for a cross section of the wire at position z in real space and wave number k. The cross section is parallel to the x, y-plane. \(\upsilon\) is the index of the eigenstate and might contain in addition a band or valley index (e.g., the six lowest valleys of the silicon conduction band). For the subband structure, we assume inversion symmetry with \(\varepsilon ^{\text {tot}}_{\upsilon }(z,k) = \varepsilon ^{\text {tot}}_{\upsilon }(z,-k)\) and that the subband energy is a continuous function of the wave number. Otherwise the dependence on the wave number is not restricted and an example is shown in Fig. 1, which does not show monotonic behavior for positive wave numbers.

Fig. 1
figure 1

The four monotonic branches with \(\eta =-2,-1,1,2\) of a w-shaped subband and two types of reflection

Full size image

The \(\upsilon\)th subband is split into monotonic branches as a function of the wave number, where the \(\eta\)th branch has the minimum energy \(\varepsilon ^{\text {min}}_{\eta ,\upsilon }(z)\) and maximum one \(\varepsilon ^{\text {max}}_{\eta ,\upsilon }(z)\). Due to the monotonic behavior, the group velocity in z direction is either positive or negative for the whole branch. In addition, in Fig. 1, two types of reflection at an energy barrier are shown. The electron moves into the positive z-direction and after reflection into the negative one. The branches with \(\eta =1,-2\) have a negative velocity and if the energy of the electron is below \(\varepsilon ^{\text {max}}_{1}\) (see the lower dashed line in Fig. 1), two possible final states after the reflection exist which satisfy conservation of the total energy. In the framework of classical transport theory, the electron ends up in the state, which is closer to the initial one, when moving into the direction after the reflection (negative direction in this case and \(\eta =2 \rightarrow \eta =1\)). If the energy is higher than \(\varepsilon ^{\text {max}}_{1}\), the usual specular reflection with \(k \rightarrow -k\) and \(\eta =2 \rightarrow \eta =-2\) occurs (upper dashed line in Fig. 1).

2.2 Real-space grid

The real space in z direction is mapped onto a grid with grid nodes \(z_i\) and \(i = 1,\dots ,N_z\). The corresponding finite volume is given by the interval \((z^{{\text {L}}}_i,z^{{\text {R}}}_i)\) with the left boundary

$$\begin{aligned} z^{{\text {L}}}_i = {\left\{ \begin{array}{ll} z_1 &{} \text { for } i=1\\ \frac{z_{i-1}+z_i}{2} &{} \text { else } \end{array}\right. } \end{aligned}$$
(1)

and the right one

$$\begin{aligned} z^{{\text {R}}}_i = {\left\{ \begin{array}{ll} \frac{z_i+z_{i+1}}{2} &{} \text { else } \\ z_{N_z} &{} \text { for } i= N_z \end{array}\right. } \ . \end{aligned}$$
(2)

The width of the finite volume in real space is

$$\begin{aligned} \varDelta z_{i} = z^{{\text {R}}}_i-z^{{\text {L}}}_i \ . \end{aligned}$$
(3)

Within a finite volume of the z grid, the subband structure is assumed to be constant with \(\varepsilon ^{\text {tot}}_{\upsilon ,i}(k) = \varepsilon ^{\text {tot}}_{\upsilon }(z_i,k)\), \(\Psi _{\upsilon ,i}(x,y;k) = \Psi _{\upsilon }(x,y;z_i,k)\) etc.

2.3 Energy grid

The total energy is mapped onto a grid with a constant spacing of \(\varDelta \varepsilon\) with nodes \(\varepsilon _j=(j-1)\varDelta \varepsilon +\varepsilon _0\) and \(j=1,\dots ,N_{\varepsilon }\). This energy grid spans at least the whole range of the total energy from the lowest \(\varepsilon ^{\text {min}}_{\eta ,\upsilon ,i}\) to the highest \(\varepsilon ^{\text {max}}_{\eta ,\upsilon ,i}\) within the device. The phase-space grid is the tensor product of the real-space and energy grids. For the sake of legibility, the indices \(\eta ,\upsilon ,i\) of a branch in phase space are combined to an index \(\alpha = (\eta ,\upsilon ,i)\). Each monotonic branch of a subband has to be mapped onto the phase-space grid with the energy index of the lowest energy \(N^{\text {min}}_{\alpha }\)

$$\begin{aligned} \varepsilon _{j=N^{\text {min}}_{\alpha }} - \frac{\varDelta \varepsilon }{2} \le \varepsilon ^{\text {min}}_{\alpha } < \varepsilon _{j=N^{\text {min}}_{\alpha }} + \frac{\varDelta \varepsilon }{2} \end{aligned}$$
(4)

and highest one \(N^{\text {max}}_{\alpha }\)

$$\begin{aligned} \varepsilon _{j=N^{\text {max}}_{\alpha }} - \frac{\varDelta \varepsilon }{2} < \varepsilon ^{\text {max}}_{\alpha } \le \varepsilon _{j=N^{\text {max}}_{\alpha }} + \frac{\varDelta \varepsilon }{2} \ . \end{aligned}$$
(5)

The finite volume in the total energy is given for \(j= N^{\text {min}}_{\alpha },\dots ,N^{\text {max}}_{\alpha }\) by the interval \((\varepsilon ^{-}_{j,\alpha },\varepsilon ^{+}_{j,\alpha })\) with the lower boundary

$$\begin{aligned} \varepsilon ^{-}_{j,\alpha } = {\left\{ \begin{array}{ll} \varepsilon ^{\text {min}}_{\alpha } &{} \text { for } j=N^{\text {min}}_{\alpha } \\ \varepsilon _{j} - \frac{\varDelta \varepsilon }{2} &{} \text { for } N^{\text {min}}_{\alpha } <j \le N^{\text {max}}_{\alpha } \end{array}\right. } \end{aligned}$$
(6)

and the upper one

$$\begin{aligned} \varepsilon ^{+}_{j,\alpha } = {\left\{ \begin{array}{ll} \varepsilon _{j} + \frac{\varDelta \varepsilon }{2} &{} \text { for } N^{\text {min}}_{\alpha } \le j < N^{\text {max}}_{\alpha } \\ \varepsilon ^{\text {max}}_{\alpha } &{} \text { for } j=N^{\text {max}}_{\alpha } \end{array}\right. } \ . \end{aligned}$$
(7)

In Fig. 2, the minimal energy of an energy branch is shown which is not exactly aligned between two grid nodes of the energy grid.

Fig. 2
figure 2

The phase space of the subband \(\upsilon\) and branch \(\eta\) (grey area). The thick solid line is the minimal total energy of the subband and the dashed one the maximal. The hatched area is the finite volume of the phase space for position \(z_i\) and energy \(\varepsilon _j\) of this subband. The velocity is either positive for all finite volumes of a given branch or negative

Full size image

The box width in energy

$$\begin{aligned} \varDelta \varepsilon _{j,\alpha } = \varepsilon ^{+}_{j,\alpha }-\varepsilon ^{-}_{j,\alpha } \end{aligned}$$
(8)

is for the lowest (and highest) finite volume often smaller than \(\varDelta \varepsilon\) and always positive due to the monotonically increasing energy \((0 < \varDelta \varepsilon _{j,\alpha } \le \varDelta \varepsilon )\). The corresponding width in wave number is given by

$$\begin{aligned} \varDelta k_{j,\alpha } = k^{+}_{j,\alpha }-k^{-}_{j,\alpha } \end{aligned}$$
(9)

with \(\varepsilon ^{\pm }_{j,\alpha } = \varepsilon ^{\text {tot}}_{\upsilon _{\alpha },i_{\alpha }}(k^{\pm }_{j,\alpha })\). This quantity can be positive or negative depending on the sign of the group velocity of the branch. We therefore introduce lower and upper limits of the k-space boxes in ascending order

$$\begin{aligned} k^{{\text {l}}}_{j,\alpha }= & {} \min \left( k^{+}_{j,\alpha }, k^{-}_{j,\alpha }\right) \end{aligned}$$
(10)
$$\begin{aligned} k^{{\text {u}}}_{j,\alpha }= & {} \max \left( k^{+}_{j,\alpha }, k^{-}_{j,\alpha }\right) \end{aligned}$$
(11)

with

$$\begin{aligned} |\varDelta k_{j,\alpha }| = k^{{\text {u}}}_{j,\alpha }-k^{{\text {l}}}_{j,\alpha } \ . \end{aligned}$$
(12)

The average velocity of the energy box is given by

$$\begin{aligned} v_{j,\alpha } = \frac{1}{h}\frac{\varDelta \varepsilon _{j,\alpha }}{\varDelta k_{j,\alpha }} . \end{aligned}$$
(13)

The energy between the lower and upper box limits is linearly interpolated in k with this velocity

$$\begin{aligned} \varepsilon _{j,\alpha }(k) = \varepsilon ^{-}_{j,\alpha } + h v_{j,\alpha } \left( k - k^{-}_{j,\alpha } \right) \ , \end{aligned}$$
(14)

which can be inverted

$$\begin{aligned} k_{j,\alpha }(\varepsilon ) = k^{-}_{j,\alpha } + \frac{\varepsilon - \varepsilon ^{-}_{j,\alpha }}{hv_{j,\alpha }} . \end{aligned}$$
(15)

The 1D density-of-states is positive by definition

$$\begin{aligned} Z_{j,\alpha } = \frac{1}{2\pi }\left| \frac{\mathrm {d}k}{\mathrm {d}\varepsilon }\right| _{j,\alpha } = \frac{1}{2\pi h} \frac{1}{|v_{j,\alpha }|} \end{aligned}$$
(16)

and constant within a box.

3 Boltzmann transport equation

The multi-subband BE describes the spatiotemporal evolution of the distribution function \(f_{\upsilon }(z,k)\), which is the density in the 2D phase space (z, k) of the \(\upsilon\)th subband [12, 28, 29]

$$\begin{aligned} \frac{\partial f_{\upsilon }}{\partial t} - \frac{1}{h} \frac{\partial \varepsilon ^{\text {tot}}_{\upsilon }}{\partial z} \frac{\partial f_{\upsilon }}{\partial k} + v_{\upsilon } \frac{\partial f_{\upsilon }}{\partial z} = \mathscr{S}_{\upsilon }\{f\} \ . \end{aligned}$$
(17)

The scattering integral describes local and instantaneous single-particle scattering including the Pauli principle [28]

$$\begin{aligned} \mathscr{S}_{\upsilon }(z,k)\{f\}&= \nonumber \\&\frac{L_{\text {sys}}}{2\pi } \sum _{\upsilon '} \int \left[ 1-f_{\upsilon }(z,k )\right] W_{\upsilon ,\upsilon '}(z,k ,k') f_{\upsilon '}(z,k') \nonumber \\&- \left[ 1-f_{\upsilon '}(z,k')\right] W_{\upsilon ',\upsilon }(z,k',k ) f_{\upsilon }(z,k ) \mathrm {d}k' \ . \end{aligned}$$
(18)

\(L_{\text {sys}}\) is the 1D system volume and \(W_{\upsilon ,\upsilon '}(z,k ,k')\) the transition rate of a scattering event from state \(\upsilon ',k'\) into \(\upsilon ,k\). The transition rate is calculated by Fermi’s Golden Rule [12, 28]

$$\begin{aligned} W_{\upsilon ,\upsilon '}(z,k,k') = \frac{2\pi }{h} \sum \limits _{\lambda } \left| M_{\lambda ,\upsilon ,\upsilon '}(z,k,k') \right| ^2 \left[ n(h \omega _{\lambda }) + \frac{1}{2} \pm \frac{1}{2} \right] \nonumber \\ \delta \left( \varepsilon ^{\text {tot}}_{\upsilon }(z,k)-\varepsilon ^{\text {tot}}_{\upsilon '}(z,k')\pm h \omega _{\lambda } \right) \ . \end{aligned}$$
(19)

The upper sign refers to emission of the energy transfer \(h \omega _{\lambda }\) of the \(\lambda\)th scattering process and the lower one to absorption. \(M_{\lambda ,\upsilon ,\upsilon '}(z,k,k')\) is the matrix element of the \(\lambda\)th scattering process. The Bose–Einstein distribution is given by

$$\begin{aligned} n(h \omega _{\lambda }) = \frac{1}{\exp \left( \frac{h \omega _{\lambda }}{k_{\text {B}}T_0}\right) -1} \ , \end{aligned}$$
(20)

where \(k_{\text {B}}T_0\) is the thermal energy for the ambient temperature \(T_0\)[28].

The electron density, for example, is given by

$$\begin{aligned} n(x,y,z) = \frac{2}{2\pi } \sum _{\upsilon }\int f_{\upsilon }(z,k ) \left| \Psi _{\upsilon }(x,y;z,k) \right| ^2 \mathrm {d}k \ , \end{aligned}$$
(21)

where the factor of two accounts for spin degeneracy.

3.1 Godunov-type stabilization

The driving force in (17) is the derivative of the total energy w.r.t. the z-coordinate [12]. In order to apply Godunov’s stabilization scheme to the BE the drift operator is moved into the interface between two adjacent cells by assuming that the subband structure is constant within a cell and changes abruptly between cells (Fig. 2) [20, 22, 30, 31]. Within a finite volume in real space, the force is now zero

$$\begin{aligned} \frac{\partial f_{\upsilon }}{\partial t} + v_{\upsilon } \frac{\partial f_{\upsilon }}{\partial z} = \mathscr{S}_{\upsilon }\{f\} \quad \text {for} \quad z^{{\text {L}}}_i< z < z^{{\text {R}}}_i \end{aligned}$$
(22)

and \(i = 1, \dots , N_z\). Box integration of the distribution function over a finite volume in phase space with the abbreviation \(\beta =(j,\eta ,\upsilon )\)

$$\begin{aligned} \bar{f}_{\beta ,i}= & {} \frac{1}{\varDelta z_{i}} \frac{1}{|\varDelta k_{\beta ,i}|} \int \limits _{z^{{\text {L}}}_i}^{z^{{\text {R}}}_i} \int \limits _{k^{{\text {l}}}_{\beta ,i}}^{k^{{\text {u}}}_{\beta ,i}} f_{\upsilon _{\beta }}(z,k) \mathrm {d}k \mathrm {d}z \\= & {} \frac{1}{\varDelta z_{i}} \frac{1}{\varDelta \varepsilon _{\beta ,i}} \int \limits _{z^{{\text {L}}}_i}^{z^{{\text {R}}}_i} \int \limits _{\varepsilon ^{-}_{\beta ,i}}^{\varepsilon ^{+}_{\beta ,i}} f_{\upsilon _{\beta }}(z,k_{\beta ,i}(\varepsilon )) \mathrm {d}\varepsilon \mathrm {d}z \end{aligned}$$
(23)

yields with (15) a distribution function which is constant within the phase space volume \((\beta ,i)\) and positive for a positive \(f_{\upsilon _{\beta }}(z,k)\). By integration of (22) over the finite volume (Godunov’s scheme), we obtain [22, 23]

$$\begin{aligned} \frac{\partial \bar{f}_{\beta ,i}}{\partial t} - \frac{f^{\star {\text {u}}}_{\beta ,i}-\bar{f}_{\beta ,i}}{|\varDelta k_{\beta ,i}|} \frac{\partial k^{{\text {u}}}_{\beta ,i}}{\partial t} + \frac{f^{\star {\text {l}}}_{\beta ,i}-\bar{f}_{\beta ,i}}{|\varDelta k_{\beta ,i}|} \frac{\partial k^{{\text {l}}}_{\beta ,i}}{\partial t} \nonumber \\ + v_{\beta ,i} \frac{f_{\beta ,i}^{\star {\text {R}}}-f_{\beta ,i}^{\star {\text {L}}}}{\varDelta z_{i}} = \mathscr{S}_{\beta ,i}\{\bar{f}\} \ . \end{aligned}$$
(24)

The time derivatives of the k-space boundaries of the phase-space cell are due to the averaging of the distribution function in (23). The distribution functions at the four edges of the rectangular phase space box

$$\begin{aligned} f^{\star {\text {u}}/{\text {l}}}_{\beta ,i}= & {} \frac{1}{\varDelta z_{i}} \int \limits _{z^{{\text {L}}}_i}^{z^{{\text {R}}}_i} f_{\upsilon _{\beta }}(z,k^{{\text {u}}/{\text {l}}}_{\beta ,i}) \mathrm {d}z \\f^{\star {\text {R}}/{\text {L}}}_{\beta ,i}= & {} \frac{1}{|\varDelta k_{\beta ,i}|} \int \limits _{k^{{\text {l}}}_{\beta ,i}}^{k^{{\text {u}}}_{\beta ,i}} f_{\upsilon _{\beta }}(z^{{\text {R}}/{\text {L}}}_i,k) \mathrm {d}k \end{aligned}$$
(25)

have to be evaluated by appropriate Riemann solvers [21] (see Sect. 3.4).

3.2 Discrete scattering integral

For the scattering integral, we assume that the distribution function is constant within a phase space cell

$$\begin{aligned} \mathscr{S}_{\beta ,i}\{\bar{f}\} \nonumber \\ = \sum _{\beta '} \left[ 1-\bar{f}_{\beta ,i}\right] W^{\text {in}}_{\beta ,\beta ',i} \bar{f}_{\beta ',i} - \left[ 1-\bar{f}_{\beta ',i}\right] W^{\text {out}}_{\beta ',\beta ,i} \bar{f}_{\beta ,i} \end{aligned}$$
(26)

with in-scattering

$$\begin{aligned} W^{\text {in}}_{\beta ,\beta ',i} = \frac{1}{h \varDelta \varepsilon _{\beta ,i}|v_{\beta ',i}|} \frac{L_{\text {sys}}}{2\pi } \nonumber \\ \int \limits _{\varepsilon ^{-}_{\beta ,i}}^{\varepsilon ^{+}_{\beta ,i}} \int \limits _{\varepsilon ^{-}_{\beta ',i}}^{\varepsilon ^{+}_{\beta ',i}} W_{\upsilon _{\beta } ,\upsilon _{\beta '}}(z_i,k_{\beta ,i}(\varepsilon ) ,k_{\beta ',i}(\varepsilon ')) \mathrm {d}\varepsilon ' \mathrm {d}\varepsilon \end{aligned}$$
(27)

and out-scattering

$$\begin{aligned} W^{\text {out}}_{\beta ',\beta ,i} = \frac{1}{h \varDelta \varepsilon _{\beta ,i}|v_{\beta ',i}|} \frac{L_{\text {sys}}}{2\pi } \nonumber \\ \int \limits _{\varepsilon ^{-}_{\beta ,i}}^{\varepsilon ^{+}_{\beta ,i}} \int \limits _{\varepsilon ^{-}_{\beta ',i}}^{\varepsilon ^{+}_{\beta ',i}} W_{\upsilon _{\beta '},\upsilon _{\beta }}(z_i,k_{\beta ',i}(\varepsilon '),k_{\beta ,i}(\varepsilon )) \mathrm {d}\varepsilon ' \mathrm {d}\varepsilon \ . \end{aligned}$$
(28)

In many models for single-particle scattering, the energy transfer and matrix element are assumed to be constant (e.g., [32]). If we furthermore assume that the energy transfer is a multiple of the energy grid spacing with \(h\omega _{\lambda } = m_{\lambda } \varDelta \varepsilon\), where \(m_{\lambda }\) is a positive integer, the discrete transition rates can be easily evaluated

$$\begin{aligned} W^{\text {in}}_{\beta ,\beta ',i} = \frac{\varDelta \varepsilon ^{\text {overlap}}_{\beta ,\beta ',i} L_{\text {sys}}}{h^2 \varDelta \varepsilon _{\beta ,i}|v_{\beta ',i}|} \nonumber \\ \sum _{\lambda } \left| M_{\lambda ,i,\beta ,\beta '}\right| ^2 \left[ n(h \omega _{\lambda }) + \frac{1}{2} \pm \frac{1}{2} \right] \delta _{j_{\beta },j_{\beta '}\mp m_{\lambda }} \ . \end{aligned}$$
(29)

The energy overlap of the initial box \((\varepsilon ^{-}_{\beta ',i},\varepsilon ^{+}_{\beta ',i})\) and final one \((\varepsilon ^{-}_{\beta ,i},\varepsilon ^{+}_{\beta ,i})\) is given by

$$\begin{aligned} \varDelta \varepsilon ^{\text {overlap}}_{\beta ,\beta ',i} = \max \left( 0,\min \left[ \varepsilon ^{+}_{\beta ,i},\varepsilon ^{+}_{\beta ',i}+(j_{\beta }-j_{\beta '})\varDelta \varepsilon \right] \right. \nonumber \\ \left. -\max \left[ \varepsilon ^{-}_{\beta ,i},\varepsilon ^{-}_{\beta ',i}+(j_{\beta }-j_{\beta '})\varDelta \varepsilon \right] \right) \ . \end{aligned}$$
(30)

A similar formula can be derived for out-scattering

$$\begin{aligned} W^{\text {out}}_{\beta ',\beta ,i} = \frac{\varDelta \varepsilon ^{\text {overlap}}_{\beta ',\beta ,i} L_{\text {sys}}}{h^2 \varDelta \varepsilon _{\beta ,i}|v_{\beta ',i}|} \nonumber \\ \sum _{\lambda } \left| M_{\lambda ,i,\beta ',\beta }\right| ^2 \left[ n(h \omega _{\lambda }) + \frac{1}{2} \pm \frac{1}{2} \right] \delta _{j_{\beta '},j_{\beta }\mp m_{\lambda }} \ . \end{aligned}$$
(31)

The energy overlap of the initial box \((\varepsilon ^{-}_{\beta ,i},\varepsilon ^{+}_{\beta ,i})\) and final one \((\varepsilon ^{-}_{\beta ',i},\varepsilon ^{+}_{\beta ',i})\) is given by

$$\begin{aligned} \varDelta \varepsilon ^{\text {overlap}}_{\beta ',\beta ,i} = \max \left( 0,\min \left[ \varepsilon ^{+}_{\beta ',i},\varepsilon ^{+}_{\beta ,i}+(j_{\beta '}-j_{\beta })\varDelta \varepsilon \right] \right. \nonumber \\ \left. -\max \left[ \varepsilon ^{-}_{\beta ',i},\varepsilon ^{-}_{\beta ,i}+(j_{\beta '}-j_{\beta })\varDelta \varepsilon \right] \right) = \varDelta \varepsilon ^{\text {overlap}}_{\beta ,\beta ',i} \end{aligned}$$
(32)

and the energy overlap is symmetric. Since the matrix element is self-adjoint, we get furthermore

$$\begin{aligned} \left| M_{\lambda ,i,\beta ',\beta }\right| ^2 = \left| M_{\lambda ,i,\beta ,\beta '}\right| ^2 \ . \end{aligned}$$
(33)

These symmetries and the choice of the energy transfer ensure that the principle of detailed balance holds at equilibrium as shown in the next section. In addition, the box integration results in a discrete scattering integral that is particle-number conserving by construction.

3.3 Principle of detailed balance

At equilibrium, the principle of detailed balance must hold [28]. With the equilibrium distribution function, which is in this case the Fermi-Dirac distribution

$$\begin{aligned} f_{\text {FD}}(\varepsilon ) = \frac{1}{1+\exp \left( \frac{\varepsilon -\mu _{\text {F}}}{k_{\text {B}}T_0}\right) } \ , \end{aligned}$$
(34)

where \(\mu _{\text {F}}\) is the Fermi energy, scattering from one state into the other must exactly equal the reverse transition

$$\begin{aligned} \left[ 1-f_{\text {FD}}(\varepsilon _{j_{\beta }})\right] W^{\text {in}}_{\beta ,\beta ',i} f_{\text {FD}}(\varepsilon _{j_{\beta '}}) \nonumber \\ = \left[ 1-f_{\text {FD}}(\varepsilon _{j_{\beta '}})\right] W^{\text {out}}_{\beta ',\beta ,i} f_{\text {FD}}(\varepsilon _{j_{\beta }}) \ . \end{aligned}$$
(35)

With (34) we obtain

$$\begin{aligned} W^{\text {in}}_{\beta ,\beta ',i} = W^{\text {out}}_{\beta ',\beta ,i} \exp \left( \frac{\varepsilon _{j_{\beta '}}-\varepsilon _{j_{\beta }}}{k_{\text {B}}T_0}\right) \ . \end{aligned}$$
(36)

The same result is obtained, if we neglect the Pauli principle and use the Boltzmann distribution. If we assume that the scattering from \(\beta '\) to \(\beta\) is an emission, the reverse process must be an absorption, and inserting the above expressions for the transition rates, we obtain, after eliminating the equivalent factors on both sides of the equation, for the \(\lambda\)th scattering process

$$\begin{aligned} \left[ n(h \omega _{\lambda }) + 1\right] \delta _{j_{\beta },j_{\beta '} - m_{\lambda }} \nonumber \\ = n(h \omega _{\lambda }) \delta _{j_{\beta '},j_{\beta } + m_{\lambda }} \exp \left( \frac{\varepsilon _{j_{\beta '}}-\varepsilon _{j_{\beta }}}{k_{\text {B}}T_0}\right) \ . \end{aligned}$$
(37)

With the Bose-Einstein distribution (20), this equality can be shown to hold, because the energy transfer of the scattering processes was aligned with the energy grid \((h \omega _{\lambda } = m_{\lambda } \varDelta \varepsilon )\), and the principle of detailed balance also holds in the discrete case.

3.4 Riemann solver for the cell interfaces

The distribution functions at the left and right boundaries of the cell in real space \(f_{\beta ,i}^{\star {\text {L}}}\), \(f_{\beta ,i}^{\star {\text {R}}}\), which occur in (24), are calculated by particle flux conservation (Riemann solver [21]). For a subband branch with a positive velocity, which is constant within an energy cell, the flux in positive z-direction at the right cell boundary is given with (13) by

$$\begin{aligned} \mathscr{F}^{\text {R pos}}_{\beta ,i}= & {} \int \limits _{k^{{\text {l}}}_{\beta ,i}}^{k^{{\text {u}}}_{\beta ,i}} f_{\upsilon _{\beta }}^{\star {\text {R}}}(z^{{\text {R}}}_i,k) v_{\beta ,i} \mathrm {d}k \ = \ v_{\beta ,i} \int \limits _{k^{{\text {l}}}_{\beta ,i}}^{k^{{\text {u}}}_{\beta ,i}} f_{\upsilon _{\beta }}^{\star {\text {R}}}(z^{{\text {R}}}_i,k) \mathrm {d}k \\= & {} \frac{\varDelta \varepsilon _{\beta ,i}}{h} f_{\beta ,i}^{\star {\text {R}}} \ = \ \bar{f}_{\beta ,i} \frac{\varDelta \varepsilon _{\beta ,i}}{h} \end{aligned}$$
(38)

with \(f_{\beta ,i}^{\star {\text {R}}} = \bar{f}_{\beta ,i}\), because all particles arriving at the right boundary of the cell must stem from within the cell due to the positive velocity [22, 23].

The case at the left boundary for a positive velocity is quite different and particles enter the phase space cell \((\beta ,i)\) from different cells under conservation of the total energy. This requires the index of the total energy \(j_{\beta }\) to be the same for the initial and final boxes, while the corresponding wave numbers and velocities can change during the transition (Fig. 2). Since the energy index does not change during the transition, spurious dispersion in energy, which occurs, when the energy grids of two adjacent cells are not aligned, is avoided. The flux at the left boundary within the cell for particles flowing into the positive z-direction

$$\begin{aligned} \mathscr{F}^{\text {L pos}}_{\beta ,i} = f_{\beta ,i}^{\star {\text {L}}} \frac{\varDelta \varepsilon _{\beta ,i}}{h} = \mathscr{F}^{\text {tr pos}}_{\beta ,i} + \mathscr{F}^{\text {re pos}}_{\beta ,i} \end{aligned}$$
(39)

is the sum of the flux transmitted from the adjacent cell to the left of the ith real-space cell \(\mathscr{F}^{\text {tr pos}}_{\beta ,i}\) and the flux of particles moving into the negative z-direction in the ith real-space cell, which are reflected into the cell with positive velocity \(\mathscr{F}^{\text {re pos}}_{\beta ,i}\). Particles can be only transmitted from the adjacent cell at the left boundary, if this cell is also in the grey area of Fig. 2 and \(N^{\text {min}}_{\eta _{\beta },\upsilon _{\beta },i-1} \le j_{\beta } \le N^{\text {max}}_{\eta _{\beta },\upsilon _{\beta },i-1}\) must hold

$$\begin{aligned} \mathscr{F}^{\text {tr pos}}_{\beta ,i} = \bar{f}_{\beta ,i-1} \frac{\varDelta \varepsilon ^{\text {tr pos}}_{\beta ,i}}{h} \end{aligned}$$
(40)

with the overlap of the energy interval of the initial box \((\varepsilon ^{-}_{\beta ,i-1},\varepsilon ^{+}_{\beta ,i-1})\) and the final one \((\varepsilon ^{-}_{\beta ,i},\varepsilon ^{+}_{\beta ,i})\)

$$\begin{aligned} \varDelta \varepsilon ^{\text {tr pos}}_{\beta ,i} = \max \left( 0,\min (\varepsilon ^{+}_{\beta ,i},\varepsilon ^{+}_{\beta ,i-1}) \right. \nonumber \\ \left. -\max (\varepsilon ^{-}_{\beta ,i},\varepsilon ^{-}_{\beta ,i-1})\right) \ . \end{aligned}$$
(41)

Since for a positive velocity the distribution function of the left cell occurs in the diffusion term of the BE (24), the derivative w.r.t. z is approximated by an upwind scheme [21]. Since the sign of the velocity does not depend on the solution variables, the upwind direction is fixed and does not change during the simulation.

Another source of particles entering the cell at the left boundary is reflection of particles traveling into the negative direction. In the case of specular reflection (the upper case in Fig. 1) with \(\eta '= -\eta\), the flux due to reflection is given with \(\bar{\beta }= (j_\beta ,-\eta _\beta ,\upsilon _\beta )\) by

$$\begin{aligned} \mathscr{F}^{\text {re pos}}_{\beta ,i} = \bar{f}_{\bar{\beta },i} \frac{\varDelta \varepsilon ^{\text {re pos}}_{\beta ,i}}{h} \end{aligned}$$
(42)

with possible barriers at the top (\(+\)) and bottom (−) of the cell boundary (Fig. 3)

$$\begin{aligned} \varDelta \varepsilon ^{\text {re}\pm \text { pos}}_{\beta ,i} = \max \left( 0,\varepsilon ^{\pm }_{\bar{\beta },i}-\varepsilon ^{\pm }_{\bar{\beta },i-1}\right) \end{aligned}$$
(43)

and the sum of those two

$$\begin{aligned} \varDelta \varepsilon ^{\text {re pos}}_{\beta ,i} = \varDelta \varepsilon ^{\text {re+ pos}}_{\beta ,i} + \varDelta \varepsilon ^{\text {re- pos}}_{\beta ,i} \ . \end{aligned}$$
(44)

In the case that the barrier at the left boundary spans the whole energy width of the cell (e.g., cell \((j-1,\eta ,\upsilon ,i-1)\) in Fig. 2), the total flux of that cell is reflected

$$\begin{aligned} \mathscr{F}^{\text {re pos}}_{\beta ,i} = \bar{f}_{\bar{\beta },i} \frac{\varDelta \varepsilon _{\bar{\beta },i}}{h} \ . \end{aligned}$$
(45)
Fig. 3
figure 3

The barriers leading to specular reflection of particles moving into the negative direction with \(\eta _{\bar{\beta }}=-\eta _{\beta }\) and \(v_{\bar{\beta },i} < 0\)

Full size image

When particles move from one cell to another, the total energy is conserved, and the sum of all energy overlaps is exactly the energy width of the cell, into which the particles enter

$$\begin{aligned} \varDelta \varepsilon _{\beta ,i} = \varDelta \varepsilon ^{\text {tr pos}}_{\beta ,i} + \varDelta \varepsilon ^{\text {re pos}}_{\beta ,i} \ . \end{aligned}$$
(46)

Particles with a total energy outside of the energy interval of this cell can not enter the cell. If there are multiple cells, which contain the same total energy overlapping with this cell, only particles from the cell, which satisfies the rules of classical transport theory (see Fig. 1), can enter. Eq. (46) ensures flux conservation (see (38)).

In the case of the second reflection type shown in Fig. 1, a similar set of equations can be derived, which contains more cases, because the cell, into which the particles are reflected, might overlap for example with the energy \(\varepsilon ^{\text {max}}_1\) and in this case both types of reflection could contribute to the flux. The corresponding formulas are cumbersome and not shown, but easy to program due to the use of the total energy and (46) still holds.

In the case of a cell with a negative velocity, the left and right boundaries have to be interchanged in the formulas and the derivation of the final expressions is straightforward and also not shown.

In the non-stationary case, the subband structure depends on time via the potential and thus the k-grid. This time dependence of the k-grid leads to additional time derivatives in the discrete BE (24) w.r.t. the k-space boundaries of the phase-space boxes (Fig. 4). The distribution functions at the upper and lower boundary of the cell in the wavenumber are given by

$$\begin{aligned} f^{\star {\text {u}}}_{j ,\eta ,\upsilon ,i} = {\left\{ \begin{array}{ll} \bar{f}_{j',\eta ',\upsilon ,i} &{} \text {for } \quad \frac{\partial k^{{\text {u}}}_{j,\eta ,\upsilon ,i}}{\partial t} > 0 \\ \bar{f}_{j ,\eta ,\upsilon ,i} &{} \text {for } \quad \frac{\partial k^{{\text {u}}}_{j,\eta ,\upsilon ,i}}{\partial t} < 0 \end{array}\right. } \end{aligned}$$
(47)

where \(j',\eta '\) are the indices of the adjacent cell in positive k-direction with \(k^{{\text {u}}}_{j,\eta ,\upsilon ,i}=k^{{\text {l}}}_{j',\eta ',\upsilon ,i}\), and

$$\begin{aligned} f^{\star {\text {l}}}_{j,\eta ,\upsilon ,i} = {\left\{ \begin{array}{ll} \bar{f}_{j ,\eta ,\upsilon ,i} &{} \text {for} \quad \frac{\partial k^{{\text {l}}}_{j,\eta ,\upsilon ,i}}{\partial t} > 0 \\ \bar{f}_{j'',\eta '',\upsilon ,i} &{} \text {for} \quad \frac{\partial k^{{\text {l}}}_{j,\eta ,\upsilon ,i}}{\partial t} < 0 \end{array}\right. } \end{aligned}$$
(48)

where \(j'',\eta ''\) are the indices of the adjacent cell in negative k-direction with \(k^{{\text {l}}}_{j,\eta ,\upsilon ,i}=k^{{\text {u}}}_{j'',\eta '',\upsilon ,i}\).Footnote 1

Fig. 4
figure 4

Choice of the value of the distribution function at the boundary of a k-space cell

Full size image

3.5 Boundary conditions for the BE

At the left interface of the first cell in real space (source contact) and at the right interface of the last cell in real space (drain contact), Dirichlet boundary conditions are applied for the inflowing particles [33, 34]. At the left interface for all \(\beta\) with a positive velocity, the distribution function is given by the Fermi-Dirac distribution (34)

$$\begin{aligned} f_{\beta ,1}^{\star {\text {L}}} = f_{\text {FD}}(\varepsilon _{j_\beta }+eV_{\text {S}}) \quad \text {for} \quad v_{\beta ,1}>0 \end{aligned}$$
(49)

and at the right one with negative velocity by

$$\begin{aligned} f_{\beta ,N_z}^{\star {\text {R}}} = f_{\text {FD}}(\varepsilon _{j_\beta }+eV_{\text {D}}) \quad \text {for} \quad v_{\beta ,N_z}<0 \ . \end{aligned}$$
(50)

\(V_{\text {S}}\), \(V_{\text {D}}\) are the source and drain potentials, respectively. The Fermi energy \(\mu _{\text {F}}\) is the energy reference and the built-in potentials at the contacts are chosen such that the contacts are charge neutral at equilibrium with \(V_{\text {S}}=V_{\text {D}}=0\). The number of particles due to the Fermi-Dirac distributions at the contacts should not change with an applied bias. This might require adjustment of the built-in potentials due to the use of a grid in total energy.

In the case of equilibrium, the Fermi-Dirac distribution leads to a vanishing scattering integral because of the principle of detailed balance. Furthermore, since the Fermi-Dirac distribution depends on the total energy and is position independent, it satisfies with (46) the diffusion term of the discrete BE (24). Since the solution is stationary at equilibrium, the time derivative also vanishes and the Fermi-Dirac distribution (34) evaluated at the box energies \(\varepsilon _j\) is the exact solution of the discrete BE at equilibrium.

4 Stability analysis

4.1 Non-negative solution of the BE

The solution of the BE is nonnegative for nonnegative boundary conditions. The discrete BE should have the same property. To show this, we will investigate the stationary case and neglect the Pauli principle. In this case, the BE is linear and results in a linear system of equations, of which the system matrix should have a nonnegative inverse. For example, an M-matrix has a nonnegative inverse [35].

The elements of the distribution function are arranged into a vector with \(\left[ \mathbf {f} \right] _{(\beta ,i)} = \bar{f}_{\beta ,i}\) for all possible indices in the grey area of Fig. 2. Similarly, the boundary conditions are assembled in a vector \(\mathbf {b}\) and the discrete BE takes the form \(\hat{A} \mathbf {f} = \mathbf {b}\) with the system matrix \(\hat{A}=\hat{D}+\hat{S}\), which is the sum of the diffusion matrix \(\hat{D}\) and scattering matrix \(\hat{S}\).

The main diagonal of an M-matrix should be positive and the off-diagonal elements nonpositive. The sum over all elements of a row should be nonnegative, and for an irreducible matrix, the sum over at least one row must be positive [35]. This is usually the case due to the boundary conditions, for which the corresponding rows of the system matrix have only a one on the main diagonal and zeros otherwise

$$\begin{aligned} \left[ \hat{A}\right] _{(\beta ,i),(\beta ',i')} = \delta _{\beta ,\beta '}\delta _{i,i'} \ . \end{aligned}$$
(51)

The diffusion term in (24) for a positive velocity \(v_{\beta ,i} > 0\) is given for specular reflection with (38),(39) by

$$\begin{aligned} v_{\beta ,i} \frac{f_{\beta ,i}^{\star {\text {R}}}-f_{\beta ,i}^{\star {\text {L}}}}{\varDelta z_{i}} \nonumber \\ = \frac{v_{\beta ,i}}{\varDelta z_{i}} \left[ \bar{f}_{\beta ,i} -\left( \bar{f}_{\beta ,i-1}\frac{\varDelta \varepsilon ^{\text {tr pos}}_{\beta ,i}}{\varDelta \varepsilon _{\beta ,i}} + \bar{f}_{\bar{\beta },i }\frac{\varDelta \varepsilon ^{\text {re pos}}_{\beta ,i}}{\varDelta \varepsilon _{\beta ,i}} \right) \right] \ . \end{aligned}$$
(52)

The corresponding nonzero entries of the diffusion matrix are on the main diagonal

$$\begin{aligned} \left[ \hat{D} \right] _{(\beta ,i),(\beta ,i)} = \frac{v_{\beta ,i}}{\varDelta z_{i}} \end{aligned}$$
(53)

and on the off-diagonals

$$\begin{aligned} \left[ \hat{D} \right] _{(\beta ,i),(\beta ,i-1)} = -\frac{v_{\beta ,i}}{\varDelta z_{i}} \frac{\varDelta \varepsilon ^{\text {tr pos}}_{\beta ,i}}{\varDelta \varepsilon _{\beta ,i}} \end{aligned}$$
(54)

and

$$\begin{aligned} \left[ \hat{D} \right] _{(\beta ,i),(\bar{\beta },i)} = -\frac{v_{\beta ,i}}{\varDelta z_{i}} \frac{\varDelta \varepsilon ^{\text {re pos}}_{\beta ,i}}{\varDelta \varepsilon _{\beta ,i}} \ . \end{aligned}$$
(55)

These three entries have the required signs and their sum is exactly zero due to (46). For a negative velocity \(v_{\beta ,i}\), the matrix entries have the same properties. Similar results are obtained for general reflections.

For the matrix to be irreducible and non-singular, scattering is required [36]. The contribution of the scattering integral to the system matrix is without the Pauli principle

$$\begin{aligned} \left[ \hat{S} \right] _{(\beta ,i),(\beta ',i')} = \left( - W^{\text {in}}_{\beta ,\beta ',i} + \sum _{\beta ''} W^{\text {out}}_{\beta '',\beta ,i} \delta _{\beta ,\beta '}\right) \delta _{i,i'} \ . \end{aligned}$$
(56)

Separation of the distribution function into the equilibrium distribution function and a positive factor \(g_{\beta ,i}\) yields

$$\begin{aligned} \bar{f}_{\beta ,i} = \exp \left( - \frac{\varepsilon _{j_{\beta }}-\mu _{\text {F}}}{k_{\text {B}}T_0} \right) g_{\beta ,i} \ . \end{aligned}$$
(57)

With the nonnegative and non-singular diagonal matrix

$$\begin{aligned} \left[ \hat{H} \right] _{(\beta ,i),(\beta ',i')} = \exp \left( - \frac{\varepsilon _{j_{\beta }}-\mu _{\text {F}}}{k_{\text {B}}T_0} \right) \delta _{\beta ,\beta '}\delta _{i,i'} \end{aligned}$$
(58)

and the vector of the factor \(\mathbf {g}\) we obtain \(\mathbf {f} = \hat{H} \mathbf {g}\). Multiplication of the system matrix from the right by \(\hat{H}\) and from the left by the inverse leads to

$$\begin{aligned} \hat{A}'= \hat{H}^{-1}\hat{A} \hat{H} = \hat{D} + \underbrace{\hat{H}^{-1}\hat{S} \hat{H}}_{=\hat{S}'} \ . \end{aligned}$$
(59)

The diffusion matrix \(\hat{D}\) is not changed by the transformation, because the elements in the rows of the diffusion matrix are nonzero only for \(j_{\beta '}=j_{\beta }\) and are therefore not modified by the transformation, which depends only on \(j_{\beta }\). The transformed scattering matrix \(\hat{S}'\) is an M-matrix due to the principle of detailed balance (36) [15]

$$\begin{aligned} \left[ \hat{S}' \right] _{(\beta ,i),(\beta ',i')} \nonumber \\ = \left( - W^{\text {in}}_{\beta ,\beta ',i} \exp \left( \frac{\varepsilon _{j_\beta }-\varepsilon _{j_{\beta '}}}{k_{\text {B}}T_0}\right) + \sum _{\beta ''} W^{\text {out}}_{\beta '',\beta ,i} \delta _{\beta ,\beta '}\right) \delta _{i,i'} \nonumber \\ = \left( - W^{\text {out}}_{\beta ',\beta ,i} + \sum _{\beta ''} W^{\text {out}}_{\beta '',\beta ,i} \delta _{\beta ,\beta '}\right) \delta _{i,i'} \ , \end{aligned}$$
(60)

where the transition rates are nonnegative. Since the sum of two M-matrices is also an M-matrix, when both matrices satisfy the row criterion, the transformed system matrix has property M. The inverse of the system matrix remains nonnegative under transformation with a nonnegative diagonal matrix and the distribution function is nonnegative by construction. Since this M matrix has only eigenvalues with positive real parts and is diagonally dominant [35], the numerical stability of the discrete BE is excellent.

4.2 Stability in the time domain

If the Pauli principle is neglected, the BE itself is linear in the distribution function, and for a stationary potential, only the first time-derivative in (24) remains

$$\begin{aligned} \frac{\partial \bar{f}_{\beta ,i}}{\partial t} + v_{\beta ,i} \frac{f_{\beta ,i}^{\star {\text {R}}}-f_{\beta ,i}^{\star {\text {L}}}}{\varDelta z_{i}} = \mathscr{S}_{\beta ,i}\{\bar{f}\} \ , \end{aligned}$$
(61)

because the time derivatives of the k-grid are zero for a stationary potential. The time derivative occurs not in the equations for the Dirichlet boundary conditions and the system of equations is rearranged such that all boundary conditions are found in the top rows

$$\begin{aligned} \left[ \begin{pmatrix} \hat{0} &{} \hat{0}\\ \hat{0} &{} \hat{I} \end{pmatrix} \frac{\partial }{\partial t} + \begin{pmatrix} \hat{I} &{} \hat{0}\\ \hat{c} &{} \hat{a} \end{pmatrix} \right] \begin{pmatrix} \mathbf {f}_{\text {DBC}}\\ \mathbf {f}_{\text {int}} \end{pmatrix} = \begin{pmatrix} \mathbf {b} \\ \mathbf {0} \end{pmatrix} \ . \end{aligned}$$
(62)

\(\mathbf {f}_{\text {DBC}}\) is the vector of the distribution-function values on the grid nodes to which Dirichlet boundary conditions are applied (see (49),(50)). \(\mathbf {f}_{\text {int}}\) contains all other values including the values for the out-flowing particles in the contacts. \(\hat{I}\) is the identity matrix of the corresponding rank. The matrix \(\hat{c}\) contains the coupling to the contact nodes for the in-flowing particles (e.g., \(\left[ \hat{D} \right] _{(\beta ,2),(\beta ,1)}\) for positive velocities). \(\hat{a}\) contains the remaining elements of \(\hat{A}\). After elimination of \(\mathbf {f}_{\text {DBC}}\), the discrete BE is given by

$$\begin{aligned} \left[ \hat{I} \frac{\partial }{\partial t} + \hat{a} \right] \mathbf {f}_{\text {int}} = - \hat{c} \mathbf {b} \ . \end{aligned}$$
(63)

After Laplace transformation from time to the complex variable s, stability requires that all poles of the BE have a negative real part. The Laplace transformation of the discrete BE yields in this case

$$\begin{aligned} \left( s\hat{I} + \hat{a}\right) \mathbf {F}_{\text {int}} = \mathbf {f}_{\text {int}}(0) - \hat{c} \mathbf {B} \ , \end{aligned}$$
(64)

where \(\mathbf {F}_{\text {int}}\), \(\mathbf {B}\) are the corresponding Laplace transforms. The poles \(s_l\) are the roots of the characteristic equation

$$\begin{aligned} \det \left( s_l\hat{I} + \hat{a} \right) = 0 \end{aligned}$$
(65)

with \(s_l=-\lambda _l\), where \(\lambda _l\) are the eigenvalues of the matrix \(\hat{a}\). Since the transformation in (59) does not change the eigenvalues of the matrix, these are also the eigenvalues of the matrix \(\hat{H}^{-1}\hat{a}\hat{H}\), which is again an M-matrix,Footnote 2 of which all eigenvalues have positive real parts [35]. Thus, all poles have negative real parts and the discrete BE is stable for a stationary potential due to Godunov’s stabilization scheme, scattering and the boundary conditions.

For a potential, which is translationally invariant in z-direction (zero force), the subband structure does not depend on z and the BE has a unique solution even in the ballistic case without scattering. The stationary distribution function within the device is given in this simple case by the boundary conditions. All poles still have a negative real part although scattering is neglected, because in this special case the diffusion matrix together with the boundary conditions yields a non-singular M-matrix. Thus, in addition to the boundary conditions [33], Godunov’s scheme introduces dissipation in the system.

To investigate this numerical dissipation, a plane wave with the real angular frequency \(\omega\) and wave number q traveling into the positive z-direction \((\omega> 0, \; \mathfrak {R}\{q\} > 0)\) is considered

$$\begin{aligned} f_{\beta }(z,t) = \mathfrak {R}\left\{ f^{0}_{\beta } \exp \left( \mathrm {j}\omega t - \mathrm {j}q z \right) \right\} \ . \end{aligned}$$
(66)

In the ballistic case, the BE (22) reduces to a linear advection equation and the dispersion relation of the plane wave is given by

$$\begin{aligned} q = \frac{\omega }{v_{\upsilon _\beta }(k)} \ . \end{aligned}$$
(67)

The wave number is real for a real frequency and the wave is not damped \((\mathfrak {I}\{q\} = 0)\) due to the assumption of zero scattering. With the ballistic discrete BE for a positive velocity and a homogeneous subband structure

$$\begin{aligned} \frac{\partial \bar{f}_{\beta ,i}}{\partial t} + v_{\beta } \frac{\bar{f}_{\beta ,i}-\bar{f}_{\beta ,i-1}}{\varDelta z_{i}} = 0 \end{aligned}$$
(68)

we obtain for an equidistant grid in z-direction with \(\varDelta z_i = \varDelta z\) the characteristic equation

$$\begin{aligned} \mathrm {j}\omega + v_{\beta } \frac{1-\exp \left( \mathrm {j}q \varDelta z\right) }{\varDelta z} = 0 \ . \end{aligned}$$
(69)

Expansion up to the second order in the frequency and wave number yields the dispersion relation

$$\begin{aligned} q \approx \frac{\omega }{v_{\beta }} - \mathrm {j}\frac{\omega ^2 \varDelta z}{2v^2_{\beta }} \ . \end{aligned}$$
(70)

Compared to the exact analytical result (67), an additional negative imaginary part occurs due to Godunov’s scheme, which leads to damping of the wave. The imaginary part is proportional to the grid spacing and thus due to the discrete formulation of the system. A finer real-space grid leads to less numerical dissipation, of which the impact is strongest at high frequencies for states with a low group velocity. Due to the artificial damping, an explicit Euler scheme is possible even in the ballistic case.

The Laplace transformation of the discrete BE (61) yields in the case with scattering and a stationary potential, which can depend on the z-coordinate, for the forward Euler scheme the characteristic equation

$$\begin{aligned} \det \left( \frac{\exp (s \varDelta t)-1}{\varDelta t} \hat{I} + \hat{a} \right) = 0 \ , \end{aligned}$$
(71)

which has the roots

$$\begin{aligned} \frac{\exp (s_l \varDelta t)-1}{\varDelta t} + \lambda _l = 0 \ . \end{aligned}$$
(72)

The real part of the poles \(s_l\) must be negative

$$\begin{aligned} \mathfrak {R}\{s_l\} = \frac{1}{\varDelta t} \ln |1-\lambda _l \varDelta t| < 0 \end{aligned}$$
(73)

and the time step must be so small that \(\lambda _l \varDelta t\) lies within the circle

$$\begin{aligned} |1-\lambda _l \varDelta t| < 1 \ . \end{aligned}$$
(74)

The eigenvalues \(\lambda _l\) have a positive real part, and with Gershgorin’s theorem [37], an upper bound for the positive time step can be calculated that satisfies (74)

$$\begin{aligned} \varDelta t< & {} \frac{1}{\max \limits _{\beta ,i} \left[ \hat{H}^{-1}\hat{a}\hat{H}\right] _{(\beta ,i),(\beta ,i)}} \ =\ \frac{1}{\max \limits _{\beta ,i} \left[ \hat{a}\right] _{(\beta ,i),(\beta ,i)}} \\< & {} \frac{1}{\max \limits _{\beta ,i} \left\{ \frac{|v_{\beta ,i}|}{\varDelta z_i} + S^{\text {out}}_{\beta ,i}\right\} } \end{aligned}$$
(75)

with the total out-scattering rate

$$\begin{aligned} S^{\text {out}}_{\beta ,i} = \sum _{\beta '} W^{\text {out}}_{\beta ',\beta ,i} \ . \end{aligned}$$
(76)

The equality in (75) holds, because the transformation does not change the main diagonal elements of the matrix \(\hat{a}\).

5 Transient simulations

Since the explicit Euler scheme is stable for the BE, we will use it to solve the BE, PE and SE self-consistently in the transient case. After discretization, the three equations form a system of differential algebraic equations, where only the BE contains a time derivative and is solved by the forward Euler scheme (see 5.1). This yields a distribution function \(\bar{f}_{j,\eta ,\upsilon ,i,l-1}^{\text { end}}\) at the end of the \(l-1\)th time step. With this distribution function, the electron density is calculated by (21) for time \(t_l\) and the PE is solved self-consistently with the SE. The coupled solution of the PE and SE is necessary, because the electron density depends on the wave functions which in turn depend on the potential. Since solving the SE results in a new subband structure \(\varepsilon ^{\text {tot}}_{\upsilon ,i,l}(k)\), the k-grid \(k^{\pm }_{j,\eta ,\upsilon ,i,l}\) has to be rebuilt for the time-invariant grid of the total energy as shown in Sect. 2.3. The change in the k-grid requires the mapping of the distribution function based on the old k-grid onto the new one. This is detailed in Sect. 5.2. After a self-consistent solution of the PE and SE is obtained, the BE is solved again by the forward Euler scheme based on the new potential and the initial condition is the old distribution function mapped onto the new k-grid.

The transient simulations are performed with two different times steps. The larger one \(\varDelta t^{\text {PE}}_l = t_l-t_{l-1}\), which is the time between updates of the PE together with the SE, is a multiple of the time step \(\varDelta t^{\text {BE}}_k = t_k-t_{k-1}\) for the BE. The time step for the BE should be at least twice as short as the stability limit (75) to obtain smoother transient solutions (i.e., the matrix in the square brackets in (77) has only eigenvalues with positive real parts). The CPU time for the calculation of the subband structure and transition rates, which has to be done every time the PE and SE are solved, is larger than the CPU time for the iteration of the BE by the forward Euler scheme, and the CPU-time increase due to multiple time steps of the BE does not dominate the total CPU time. This makes it possible to use time steps for the PE similar to the MC method [38, 39].

The explicit time integration scheme avoids the solution of large linear systems of equations and does not, therefore, require much memory. Furthermore, the explicit scheme can be efficiently parallelized.

5.1 Forward Euler scheme for the discrete BE

The discrete BE with the time derivative (63) integrated by the forward Euler scheme is given for the time step \(\varDelta t^{\text {BE}}_k\) by

$$\begin{aligned} \mathbf {f}_{\text {int},k} = \left[ \hat{I} - \varDelta t^{\text {BE}}_k \hat{a} \right] \mathbf {f}_{\text {int},k-1} - \varDelta t^{\text {BE}}_k \hat{c} \mathbf {b} \ . \end{aligned}$$
(77)

For the distribution function \(\mathbf {f}_{\text {int},k}\) at time \(t_k\) to be nonnegative, the right-hand side of this equation must be nonnegative. The matrix \(-\hat{c}\) and the vector \(\mathbf {b}\) are both nonnegative as is the distribution function \(\mathbf {f}_{\text {int},k-1}\). The matrix in the square brackets is nonnegative, because the off-diagonal elements of \(-\hat{a}\) are nonnegative and the main diagonal elements of \(\hat{I} - \varDelta t^{\text {BE}}_k \hat{a}\) are positive, if \(\varDelta t^{\text {BE}}_k\) satisfies (75). Thus, a positive distribution function remains positive during the iteration of the forward Euler scheme.

If the Pauli principle is included in the scattering integral, the total out-scattering rate is an upper bound of the contribution of the scattering integral to the main diagonal

$$\begin{aligned} \sum _{\beta ''} \left[ 1-\bar{f}_{\beta ',i,k-1}\right] W^{\text {out}}_{\beta ',\beta ,i} < S^{\text {out}}_{\beta ,i} \ . \end{aligned}$$
(78)

With (75) and a distribution function, which is smaller than one, this ensures a positive distribution function in the case of the nonlinear scattering integral. Similar arguments show that a distribution function, which is smaller than one, remains smaller than one during the iteration.

5.2 Mapping of the distribution function onto a new k-grid

It is assumed that the distribution function does not change in k-space, when the subband structure is changed abruptly in time and the forces remain finite. The distribution function at the end of time step \(l-1\) is mapped onto the distribution function at the beginning of time step l

$$\begin{aligned} \bar{f}_{j,\eta ,\upsilon ,i,l}^{\text { begin}} = \frac{1}{|\varDelta k_{j,\eta ,\upsilon ,i,l}|} \int \limits _{k^{{\text {l}}}_{j,\eta ,\upsilon ,i,l}}^{k^{{\text {u}}}_{j,\eta ,\upsilon ,i,l}} \bar{f}_{\upsilon ,i,l-1}^{\text { end}}(k) \mathrm {d}k \ . \end{aligned}$$
(79)

The distribution function \(\bar{f}_{\upsilon ,i,l-1}^{\text { end}}(k)\) is piecewise constant in k-space (23) and the integral reduces to a sum over all boxes of the old k-grid for a given subband \(\upsilon\) at the ith position in real space

$$\begin{aligned} \bar{f}_{j,\eta ,\upsilon ,i,l}^{\text { begin}} = \sum _{j',\eta '} \frac{k^{\text {overlap}}_{j,\eta ,\upsilon ,i,l;j',\eta '}}{|\varDelta k_{j,\eta ,\upsilon ,i,l}|} \bar{f}_{j',\eta ',\upsilon ,i,l-1}^{\text { end}} \end{aligned}$$
(80)

with the overlap between the old and new k-space boxes

$$\begin{aligned} k^{\text {overlap}}_{j,\eta ,\upsilon ,i,l;j',\eta '} = \max \left( 0, \min \left( k^{{\text {u}}}_{j,\eta ,\upsilon ,i,l},k^{{\text {u}}}_{j',\eta ',\upsilon ,i,l-1}\right) \right. \nonumber \\ \left. - \max \left( k^{{\text {l}}}_{j,\eta ,\upsilon ,i,l},k^{{\text {l}}}_{j',\eta ',\upsilon ,i,l-1}\right) \right) \end{aligned}$$
(81)

The sum over the branches is necessary, because a minimum or maximum might shift in k-space due to a change in the potential leading to an overlap of two different branches of the same subband. The ratio of the k-space boxes in (80) is always nonnegative

$$\begin{aligned} \frac{k^{\text {overlap}}_{j,\eta ,\upsilon ,i,l;j',\eta '}}{|\varDelta k_{j,\eta ,\upsilon ,i,l}|} \ge 0 \end{aligned}$$
(82)

and the sum of the ratios over a single subband yields exactly one

$$\begin{aligned} \sum _{j',\eta '} \frac{k^{\text {overlap}}_{j,\eta ,\upsilon ,i,l;j',\eta '}}{|\varDelta k_{j,\eta ,\upsilon ,i,l}|} = 1 \ . \end{aligned}$$
(83)

This ensures that a nonnegative distribution function remains nonnegative

$$\begin{aligned} \bar{f}_{j,\eta ,\upsilon ,i,l-1}^{\text { end}} \ge 0 \quad \rightarrow \quad \bar{f}_{j,\eta ,\upsilon ,i,l}^{\text { begin}} \ge 0 \ , \end{aligned}$$
(84)

that its maximum value does not increase

$$\begin{aligned} \max _{j,\eta }(\bar{f}_{j,\eta ,\upsilon ,i,l-1}^{\text { end}}) \ge \max _{j,\eta }(\bar{f}_{j,\eta ,\upsilon ,i,l}^{\text { begin}}) \ , \end{aligned}$$
(85)

and that the number of particles in the \(\upsilon\)th subband and ith real-space box is conserved

$$\begin{aligned} \sum _{j,\eta }\bar{f}_{j,\eta ,\upsilon ,i,l-1}^{\text { end}}|\varDelta k_{j,\eta ,\upsilon ,i,l-1}| = \sum _{j,\eta }\bar{f}_{j,\eta ,\upsilon ,i,l}^{\text { begin}}|\varDelta k_{j,\eta ,\upsilon ,i,l }| \ . \end{aligned}$$
(86)

This mapping ensures that a distribution function with values between zero and one stays in this interval.

The approach is consistent with the choice of the distribution function at the upper and lower boundaries of the phase space cells in (47),(48). If the subband structure does not change, the distribution function remains the same. On the other hand, for a transient change in the band structure, charge diffuses in the k-space from cells with a larger distribution function to cells with a lower one. While the grid in total energy suppresses diffusion in the k-space for stationary simulations, this is no longer the case for transient ones.

6 Simulation results

We simulate the same silicon nanowire NMOSFET as in Ref. [22] based on a parabolic conduction band with six elliptical valleys. The lattice temperature is in all cases 300K. The silicon cuboid has a cross section of 5 nm\(\times\) 4 nm and a length of 32 nm. The gate length is 16 nm and the source/drain regions are each 8 nm long. The donor concentration is in the drain/source regions \(1\times 10^20 cm^-3\), and the channel is undoped. The perfectly insulating gate oxide with the permittivity of SiO\(_2\) has a thickness of 1 nm and the work function of the gate is 4.3eV. The channel direction is aligned with the \(\langle 100 \rangle\)-axis, which in turn is aligned with the z-axis. The grid spacings in the cross section are 0.5 nm in the x and y-directions and, if not mentioned otherwise, 0.5 nm in the z-direction as well. The energy grid has a spacing of 5meV. We include all subbands in an energy range of 0.6eV above the lowest subband edge in the source resulting in up to 6 subbands per valley. If not stated otherwise, all simulations are performed with a k-grid aligned with the total energy (H-transform).

In the stationary case, we solve the nonlinear BE by the Newton-Raphson method, where the resultant linear system of equations is solved by a GMRES with the ILUT preconditioner [40, 41]. The discrete SE is solved by the LAPACK routine DSYEV [42] and the PE by PARDISO [43]. All three equations are self-consistently solved by a Gummel loop, where the nonlinear charge term of the PE is based on imrefs [44]. The iteration is stopped, when the change in potential is less than 1\(\mu \hbox {v}\). In the transient case, the matrix-free forward Euler method is applied to the BE. The self-consistent solution of the SE and PE is obtained by a damped Picard iteration, where the charge term of the linear PE is based on the distribution functions evaluated by the BE (21). In contrast to Ref. [22], the SE is not solved in the real space but for a sine base leading to more accurate results for a real space grid in the cross section with a spacing of 0.5 nm, which is sufficiently fine for the PE [27].

The nanowire NMOSFET was simulated for diffusive and quasi-ballistic transport. In the case of diffusive transport, the original scattering integral is used, of which the scattering parameters are adjusted to match a mobility of about \(100cm^2V^-1s^-1\) in the channel resulting in strongly diffusive transport [45, 46]. For the quasi-ballistic simulations, the complete scattering integral is scaled by a factor of \(10^{-4}\) and the impact of scattering is negligible. The simulations include 65 grid nodes in z-direction and \(15 \times 13\) grid nodes in the cross section. For the bias point \(V_\text {GS}=V_\text {DS}=0.5V\), the number of variables of the distribution function is 680550. The CPU time on a single core of a current CPU is for this bias point about 48min.

An advantage of the k-grid aligned with the total energy is that it does not suffer from spurious k-space diffusion in the stationary case [24]. To demonstrate this, in Fig. 5, the distribution function is shown for a quasi-ballistic simulation not only with a k-grid that is aligned with the total energy (H-transform) but also with one that does not depend on the position in real space (fixed k-grid, compare Ref. [22]). In the case of the H-transform, the distribution function in the drain shows the expected abrupt increase at a large value of the positive wave number. This is due to electrons from the source, which pass the source/channel barrier. Since scattering is neglected, the threshold behavior of the energy barrier is preserved when the particles move with constant total energy through the channel and drain. In the case of the fixed k-grid, diffusion occurs and the abrupt change in the distribution function is smeared out over the wave number. In both cases, the distribution functions are positive and show no artificial oscillations.

Fig. 5
figure 5

Distribution function of the lowest subband in the drain at \(V_\text {GS}=0.5\) V and \(V_\text {DS}=0.1\) V for the H-transform and a fixed k-grid in the quasi-ballistic case

Full size image

In Fig. 6, the transfer characteristics of the nanowire transistor are shown at \(V_\text {DS}=0.5\) V. With and without scattering, smooth results are obtained over many orders of magnitude. The subthreshold slope is 64 mV/dec with scattering and 63 mV/dec without at \(V_\text {GS}=0.15\) V. It does not depend on the spacing of the energy grid, which was checked by simulations with different spacings (not shown). This is in contrast to the fixed k-grid, which leads to artificial diffusion in the k-space (cf. Fig. 5), which degrades the subthreshold slope [24]. On the other hand, this does not mean that simulations based on the fixed k-grid fail catastrophically as shown in Ref. [20], where good results for the subthreshold slope were obtained with a feasible number of grid points in the k-space.

Fig. 6
figure 6

Transfer characteristics of the nanowire NMOSFET for diffusive and quasi-ballistic transport at \(V_\text {DS}=0.5\) V

Full size image

In the remainder of the paper, only the case of the H-transformed grid is discussed. The output characteristics are shown for diffusive and quasi-ballistic transport in Figs. 7, 8, respectively. The currents are smooth for both types of transport, where the lower output resistance in the quasi-ballistic case leads to better saturation of the drain current. The distribution function is for all bias points between zero and one, and does not show any spurious oscillations. At zero drain/source bias, it is given with very high accuracy by the Fermi-Dirac distribution and the scattering integral satisfies the principle of detailed balance as shown Sect. 3.3. The results in Figs. 5, 6, 7, 8 for the quasi-ballistic case demonstrate the excellent stability of Godunov’s scheme.

Fig. 7
figure 7

Output characteristics of the nanowire NMOSFET for diffusive transport

Full size image
Fig. 8
figure 8

Output characteristics of the nanowire NMOSFET for quasi-ballistic transport

Full size image

The on-switching is simulated by ramping \(V_\text {GS}\) within 10 fs from 0 V to 0.5 V at \(V_\text {DS}=0.5\) V. The time step for the PE is \(\varDelta t^\text {PE} = 0.5\) fs and for the BE \(\varDelta t^\text {BE} = 0.1\) fs. The latter value is about three times smaller than the upper limit given by (75). The CPU time for a simulation of one picosecond on a single core is 300 h. Within the first 10 fs, the gate and drain currents are dominated by the displacement current due to the linear increase in the gate voltage (Fig. 9), where the gate current is positive and the drain current negative. After the charge buildup under the gate, the drain current changes sign and remains positive. In the quasi-ballistic case, plasma oscillations are visible in the drain and gate currents for more than 100 fs, whereas in the diffusive case these are strongly damped. In both cases, the turn-on time is less than 200fs.

Fig. 9
figure 9

Absolute value of the gate and drain currents for on-switching within 10fs from \(V_\text {GS}=0.0\) V to 0.5 V at \(V_\text {DS}=0.5\) V

Full size image

In Fig. 10, the drain current is shown as a function of the scaling factor of the scattering integral for different spacings of the real-space grid. For small values of the factor, the transport is ballistic and saturates at a value, which is almost independent of the grid spacing in z-direction. At large factors, the transport is diffusive and the current should be inversely proportional to the factor, which is not the case. Instead, the current saturates at a level, which depends on the grid spacing. For smaller grid spacings, the current is longer inversely proportional to the factor and saturates at a lower level.

Fig. 10
figure 10

Drain current at \(V_\text {GS}=0.5\) V and \(V_\text {DS}=0.5\) V for different grid spacings in z-direction as a function of the scaling factor for the scattering integral

Full size image

This erroneous behavior is a consequence of the asymmetry of the upwind scheme in conjunction with the constant reconstruction of the distribution function. In the case of very strong scattering, the distribution function is very close to the equilibrium one. Let us assume that the Pauli principle can be neglected, that the difference in subband energy between two adjacent cells in real space is zero and that the left cell has a higher electron density than the right one. In this case, all electrons with a positive velocity in the left cell move to the right and all electrons with a negative velocity in the right cell move to the left. Since the distribution function is very close to the equilibrium one, the modulus of the average velocity of particles moving to the left and right is the same and does not depend on the particle density (so-called injection velocity [47]). Since the current is proportional to the product of this velocity and the density, the difference in the particle densities in the left and right cells means that the currents in positive and negative direction do not cancel each other and lead to a finite total current which depends only on the difference in the density. A finer grid in real space leads to a smaller difference in the density between adjacent cells and therefore to a smaller saturation current (Fig. 10).Footnote 3 The problem could be alleviated by using instead of the constant reconstruction of Godunov’s scheme a higher order one within a cell, but this is not trivial and might cause other problems [21]. Nevertheless, as always in the case of finite difference schemes, it has to be checked that the grid is sufficiently fine to ensure an acceptable discretization error.

The stability of the transient simulations depends on the time between successive solutions of the PE [39]. This is demonstrated in Fig. 11 for the response of the drain current to a small voltage pulse applied to the drain for quasi-ballistic transport and a constant \(\varDelta t^\text {BE}=0.1\) fs. A time step of \(\varDelta t^\text {PE}=2\) fs leads to instability and the current response does not vanish at large times. The simulations are stable for time steps of \(\varDelta t^\text {PE}=1\) fs or less. The value of \(\varDelta t^\text {PE}=0.5\) fs, which was used in all other transient simulations, gives good results.

Fig. 11
figure 11

Absolute value of the impulse response of the transistor at \(V_\text {GS}=0.5\) V, \(V_\text {DS}=0.0\) V for quasi-ballistic transport

Full size image

Fourier transformation of the impulse response yields the drain self-admittance (Fig. 12). Below 10 THz (Fig. 12), the impact of the different time steps can be ignored and a time step of \(\varDelta t^\text {PE}=1\) fs seems to be adequate.

Fig. 12
figure 12

Real part of the drain self-admittance \(Y_\text {DD}\) versus frequency at \(V_\text {GS}=0.5\) V, \(V_\text {DS}=0\) V for quasi-ballistic transport

Full size image

In Fig. 13, the drain self-admittance is shown for three different spacings of the grid in z-direction and \(\varDelta t^\text {PE}=0.5\) fs, \(\varDelta t^\text {BE}=0.1\) fs. The quasi-ballistic case is simulated, because the plasma oscillations are not damped by scattering. At low frequencies, the dependence on the grid spacing is weak as expected (see Fig. 10). Since the numerical damping, which occurs mainly at high frequencies, decreases with decreasing grid spacing (cf. (70)), the impact of the grid spacing is much stronger at high frequencies, where plasma oscillations occur. On the other hand, frequencies of 10 THz and more are technically not relevant in silicon and the impact of the numerical damping of Godunov’s scheme can be ignored.

Fig. 13
figure 13

Real part of the drain self-admittance \(Y_\mathrm {DD}\) versus frequency at \(V_\text {GS}=0.5\) V, \(V_\text {DS}=0\) V for quasi-ballistic transport

Full size image

7 Conclusions

We have shown that the discrete BE can be formulated with Godunov’s scheme in such a way that it is numerically very robust. Its system matrix is diagonally dominant and the distribution function is positive in the stationary and transient cases, where in the latter case the time step of the forward Euler scheme must satisfy the limit derived in the paper. If the Pauli principle is included in the scattering integral, the transient distribution function remains in the interval between zero and one. The transient solution of the BE and PE can be performed CPU and memory efficiently by the matrix-free forward Euler method, which can be easily parallelized on a computer cluster. Since Godunov’s scheme is based on the asymmetric upwind scheme, care has to be taken that the grid in real space is sufficiently fine to reduce numerical errors to an acceptable level.