Abstract
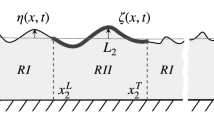
The effect of initial disturbances and unsteady external loading on an elastic beam of finite length which floats freely on the surface of an ideal incompressible fluid is studied in a linear treatment. The fluid flow is considered potential. The beam deflection is sought in the form of an expansion in the eigenfunctions of beam vibrations in vacuum with time-dependent amplitudes. The problem reduces to solving an infinite system of integrodifferential equations for unknown amplitudes. The memory functions entering this system are determined by solving the radiation problem. The beam behavior is studied for various loads with and without allowance for the weight of the fluid. The effect of fluid depth on beam deformation was determined by comparing with the previously obtained solutions of the unsteady problem for a beam floating in shallow water.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
E. Watanabe, T. Utsunomiya, and C. M. Wang, “Hydroelastic analysis of pontoon-type VLFS: A literature survey,” Eng. Struct., 26, 245–256 (2004).
I. V. Sturova, “Unsteady behavior of an elastic beam floating in shallow water under external loading,” J. Appl. Mech. Tech. Phys., 43,3, 415–423 (2002).
M. H. Meylan, “Spectral solution of time-dependent shallow water hydroelasticity,” J. Fluid Mech., 454, 387–402 (2002).
M. H. Meylan, C. Hazard, and F. Loret, “Linear time-dependent motion of a two dimensional floating elastic plate in finite depth water using the Laplace transform,” in: Proc. of the 19th Int. Workshop on Water Waves and Floating Bodies (Cortona, Italy, March 28–31, 2004), INSEAN, Rome (2004).
I. V. Sturova, “The action of an unsteady external load on a circular elastic plate floating in shallow water,” J. Appl. Math. Mech., 67, No.3, 407–416 (2003).
M. Kashiwagi, “A time-domain mode-expansion method for calculating transient elastic responses of a pontoon-type VLFS,” J. Mar. Sci. Technol., 5, No.2, 89–100 (2000).
M. Kashiwagi, “Transient responses of a VLFS during landing and take-off of an airplane,” J. Mar. Sci. Technol., 9, No. 1, 14–23 (2004).
A. Korobkin, “Unsteady hydroelasticity of floating plates,” J. Fluids Struct., 14, 971–991 (2000).
I. V. Sturova and A. Korobkin, “Two-dimensional problem of periodic loading of an elastic plate floating on the surface of an infinitely deep fluid,” J. Appl. Mech. Tech. Phys., 46, 3, 355–365 (2005).
D. E. Kheisin, Dynamics of an Ice Cover [in Russian], Gidrometeoizdat, Leningrad (1967).
Author information
Authors and Affiliations
Additional information
__________
Translated from Prikladnaya Mekhanika i Tekhnicheskaya Fizika, Vol. 47, No. 1, pp. 85–94, January–February, 2006.
Rights and permissions
About this article
Cite this article
Sturova, I.V. Unsteady Behavior of an Elastic Beam Floating on the Surface of an Infinitely Deep Fluid. J Appl Mech Tech Phys 47, 71–78 (2006). https://doi.org/10.1007/s10808-006-0010-7
Received:
Issue Date:
DOI: https://doi.org/10.1007/s10808-006-0010-7