Test collection reliability: a study of bias and robustness to statistical assumptions via stochastic simulation

Abstract

The number of topics that a test collection contains has a direct impact on how well the evaluation results reflect the true performance of systems. However, large collections can be prohibitively expensive, so researchers are bound to balance reliability and cost. This issue arises when researchers have an existing collection and they would like to know how much they can trust their results, and also when they are building a new collection and they would like to know how many topics it should contain before they can trust the results. Several measures have been proposed in the literature to quantify the accuracy of a collection to estimate the true scores, as well as different ways to estimate the expected accuracy of hypothetical collections with a certain number of topics. We can find ad-hoc measures such as Kendall tau correlation and swap rates, and statistical measures such as statistical power and indexes from generalizability theory. Each measure focuses on different aspects of evaluation, has a different theoretical basis, and makes a number of assumptions that are not met in practice, such as normality of distributions, homoscedasticity, uncorrelated effects and random sampling. However, how good these estimates are in practice remains a largely open question. In this paper we first compare measures and estimators of test collection accuracy and propose unbiased statistical estimators of the Kendall tau and tau AP correlation coefficients. Second, we detail a method for stochastic simulation of evaluation results under different statistical assumptions, which can be used for a variety of evaluation research where we need to know the true scores of systems. Third, through large-scale simulation from TREC data, we analyze the bias of a range of estimators of test collection accuracy. Fourth, we analyze the robustness to statistical assumptions of these estimators, in order to understand what aspects of an evaluation are affected by what assumptions and guide in the development of new collections and new measures. All the results in this paper are fully reproducible with data and code available online.

1 Introduction

The purpose of evaluating an information retrieval (IR) system is to predict how well it would satisfy real users. The main tool used in these evaluations are test collections, comprising a corpus of documents to search, a set of topics, and a set of relevance judgments with information as to what documents are relevant to the topics (Sanderson 2010). Given the documents returned by a system for a topic, effectiveness measures like Average Precision are used to score systems based on the relevance judgments. After running the systems with all topics in the collection, the average score is reported as the main indicator of system effectiveness, estimating the expected performance of the system for an arbitrary new topic. When comparing two systems, the main indicator reported is the average effectiveness difference, based on which we conclude which system is better.

A question raises immediately: how reliable are our conclusions about system effectiveness? (Tague-Sutcliffe 1992). Ideally, we would evaluate systems with all possible topics that users might conceive; this would imply that the true mean performance of the systems corresponds to the observed mean scores computed with the collection. But sure enough, building such a collection is either impractical for requiring an enormous amount of topics and relevance judgments, or just plain impossible if the potential set of topics is infinite or not well-defined. Therefore, the topics in a test collection must be regarded as a sample from a universe of topics, and the observed mean scores as mere estimates of the true means, erroneous to some degree. The results may change drastically with a different topic set, so much that differences between systems could even be reversed. This issue is closely related to the statistical precision of our estimates. If $D_1,D_2,\dots$ are the differences observed between two systems with a test collection, we know that the observed mean $\overline{D}$ bears some random error due to the sampling of topics. In fact, its sampling distribution has variance $\sigma ^2(D)/n_t$, where $n_t$ is the number of topics, clearly showing that our confidence in the conclusions depend not only on the observed score, but also on the variability and the number of topics used. If the observed difference is large, or the variability small, we can be confident that it is real. If not, we need to increase the number of topics to gain statistical precision.

We are therefore interested in quantifying and minimizing the estimation error. On the one hand, researchers want to estimate how well the results from an existing collection reflect the true scores of systems, that is, the accuracy of the collection. On the other hand, they want to estimate the expected accuracy of a collection with a certain number of topics, that is, the reliability of a collection design. A number of papers in the last 15–20 years have studied this issue of IR evaluation. Early work suggested the use of ad hoc, easy to understand measures for assessing the accuracy of a test collection, such as the Kendall $\tau$ correlation (Voorhees et al. 1998; Kekäläinen 2005; Sakai and Kando 2008), swap rates (Buckley and Voorhees 2000; Sakai 2007), sensitivity (Voorhees and Buckley 2002; Sanderson and Zobel 2005; Sakai 2007) or the newer Average Precision correlation (Yilmaz et al. 2008) and $d_{rank}$ distance (Carterette 2009). Some others suggested the use of measures based on statistical theory, such as procedures for significance testing (Hull 1993; Zobel 1998; Sakai 2006; Smucker et al. 2009) coupled with power analysis (Webber et al. 2008; Sakai 2014a, b) or classical test theory and generalizability theory (Bodoff and Li 2007; Carterette et al. 2009). Urbano et al. (2013b) recently reviewed many of these measures and found that they can be quite unstable. They also found clear discrepancies among measures, as already observed for instance by Sakai (2007).

All measures quantify in some way how close the scores observed with a test collection are to the true scores. The problem though, is that in practice we do not know the true system scores, so much of the previous work was devoted to develop estimators from existing data. Ad hoc measures are not founded on statistical theory, so they are estimated through extrapolation of the trends observed with randomized topic set splits, as if one were the actual collection and the other one were the true scores. Statistical measures, on the other hand, are estimated via inference using simple equations parameterized by the topic set size. All past research is thus limited in the sense that we do not know how accurate these estimators really are, because we just do not know the true system scores and therefore we can not know how close our estimates are to the true accuracy of the collections. This is a very important issue in practice, because these estimators could be biased and tell us that collections are more accurate than they really are, or that some fixed number of topics is more reliable than it actually is; we just do not know. For instance, it is impossible to know the true Type I and Type II errors of significance tests (Cormack and Lynam 2006), so we resort to approximations such as conflict ratios similarly computed through split-half designs (Zobel 1998; Sanderson and Zobel 2005; Voorhees et al. 2009; Urbano et al. 2013a).

This is particularly important for statistical measures, because they make a number of assumptions that are, by definition, not met in IR evaluation experiments (van Rijsbergen 1979; Hull 1993). The main reason is that effectiveness measures produce discrete values typically bounded by 0 and 1 (Carterette 2012). For instance, some measures of collection accuracy assume that score distributions are normally distributed;¹ they are not because they are bounded. Other measures assume homoscedasticity, that is, equal variance across systems. Webber et al. (2008) showed that IR evaluations violate this assumption as well, which can be derived again from the fact that scores are bounded. Another typical assumption is that effects are uncorrelated, which again does not hold because of the bounds.² Finally, all measures assume that the topics are a (uniform) random sample from the universe of topics and therefore constitute a representative sample. While it is fair to assume random samples in practice, the process by which topics are created may result in biased samples because they are created by humans who incorporate their own biases into the collection (Voorhees et al. 1998). In IR evaluation, we thus find non-normal distributions, heteroscedasticity, correlated effects and, usually, random sampling. Figure 1 shows some examples.

Fig. 1

Examples of violations of statistical assumptions in some TREC systems. Top clearly non-normal distribution of Reciprocal Rank scores for a system, and the corresponding residuals that closely resemble a normal distribution; the red line is the density function of a normal distribution with the same variance and mean zero. Bottom correlation between topic mean scores and system residuals, and between the residuals of two systems. See Sect. 3.2 for the definition of these effects (Color figure online)

In this paper we study all these issues of test collection reliability. Our main contributions are:

• A discussion about the concepts of accuracy and reliability of IR test collections. We review several measures to quantify the accuracy of collections, as well as estimators of the accuracy of an existing collection, and the expected accuracy of a particular collection design.

• To overcome the problem of not knowing the true system scores, we propose an algorithm for stochastic simulation of evaluation results where the true system scores are fixed upfront. It simulates a collection of arbitrary size from a given collection representing the systems and universe of topics to simulate from. The algorithm can simulate collections under all combinations of the above assumptions, and we show that it produces realistic results.

• Through large-scale simulation, we quantify for the first time the bias of the estimators of Kendall $\tau$, $\tau _{AP}$, $\text {E}\rho ^2$ and other measures of test collection accuracy. In fact, we show that the traditional estimators are biased and tend to underestimate the true accuracy of collections.

• We also study how robust these estimators are to the assumptions of normality, homoscedasticity, uncorrelated effects and (uniform) random sampling. Our results show that the first two do not seem to affect IR evaluation, and that the effect of non-random sampling appears to be minor.

• We propose two statistical estimators of the Kendall $\tau$ and $\tau _{AP}$ correlations, called $\text {E}\tau$ and $\text {E}\tau _{AP}$, and show that they are unbiased and behave much better than the typical split-half extrapolations.

The remainder of the paper is organized as follows. In Sect. 2 we review the concepts of accuracy and reliability applied to IR evaluation, in Sect. 3 we review several ad hoc and statistical measures proposed in the literature, and in Sect. 4 we discuss how they are estimated from past data. In Sect. 4.3 we propose $\text {E}\tau$ and $\text {E}\tau _{AP}$. In Sect. 5 we propose the algorithm for stochastic simulation of evaluation results. Through large-scale simulation from past TREC data, in Sect. 6 we review the bias of the estimators of the accuracy of an existing collection, and in Sect. 7 we review their bias to estimate the accuracy of a new collection of arbitrary size; in both sections, we also review their robustness to statistical assumptions. Finally, in Sects. 8 and 9 we finish with a discussion of results, the conclusions of the paper and proposals for further research. All the results in this paper are fully reproducible with data and code available online at http://github.com/julian-urbano/irj2015-reliability.

2 Evaluation accuracy and reliability

Let us consider a first scenario where a researcher wants to evaluate a fixed set of $n_s$ systems and there is a test collection $\mathbf {X}$ available with $n_t$ topics. Let $\mathbf {\mu }$ be the vector of $n_s$ true mean scores of the systems according to some effectiveness measure. Our goal when using the collection $\mathbf {X}$ is to estimate those true scores accurately, and this accuracy may be defined differently depending on the needs and goals of the researcher. For example, if we were interested in the absolute mean scores of the systems, we could define accuracy as the mean squared error over systems: $MSE (\mathbf {X},\mathbf {\mu })=\frac{1}{n_s}\sum _s{(\overline{X}_s - \mu _s)^2}$. If we were interested just in the ranking of systems, we could use the Kendall $\tau$ correlation coefficient instead. In general, we can define accuracy as a function A that compares the results of a given test collection with the true scores. The problem is that we can not compute the actual accuracy $A(\mathbf {X},\mathbf {\mu })$ because the true system scores are unknown. The approach here is to use some function $f_A$ as an estimator of the collection accuracy:

$$\begin{aligned} \hat{A}(\mathbf {X},\mathbf {\mu })=f_A(\mathbf {X}). \end{aligned}$$

(1)

The second scenario is that of a researcher building a new test collection $\mathbf {X}'$ to evaluate a fixed set of $n_s$ systems, and who wants to figure out a suitable number of topics to ensure some level of accuracy. In this case, we are not interested in how accurate a particular collection is, but rather in how accurate a hypothetical collection with $n_t'$ topics is expected to be³: $\varvec{E}_{n_t'}A(\mathbf {X}',\mathbf {\mu })$. This expectation naturally leads us to consider the reliability of a topic set size: an amount of topics can be considered reliable to the extent that a new collection of that size is expected to be accurate. Let us therefore define reliability as a function $R_A(\mathbf {X},n_t',\mathbf {\mu })=\varvec{E}_{n_t'}A(\mathbf {X}',\mathbf {\mu })$. Unfortunately, we are in he same situation as before and the true system scores remain unknown. The approach is similarly to use some function $g_A$ as an estimator of the expected collection accuracy:

$$\begin{aligned} \hat{R}_A(\mathbf {X},n_t',\mathbf {\mu })=g_A(\mathbf {X},n_t'). \end{aligned}$$

(2)

An important characteristic of $f_A$ and $g_A$ is their bias. If we were measuring collection accuracy in terms of the Kendall $\tau$ correlation and the estimator $f_A$ were positively biased, we expect it to be overestimating the correlation. This would mean that our ranking of systems is not as close to the true ranking as $f_A$ tells us. Similarly, $g_A$ would tell us that a certain number of topics, say 50, is expected to produce a correlation of 0.9, when in reality it is lower. The bias is defined as:

$$\begin{aligned} bias(f_A)&= \varvec{E}_{\mathbf {X}}\bigl [ \hat{A}(\mathbf {X},\mathbf {\mu }) - A(\mathbf {X},\mathbf {\mu }) \bigr ] \nonumber \\&=\varvec{E}_{\mathbf {X}}\bigl [ f_A(\mathbf {X}) - A(\mathbf {X},\mathbf {\mu }) \bigr ], \end{aligned}$$

(3)

$$\begin{aligned} bias(g_A)&= \varvec{E}_{\mathbf {X}}\bigl [ \hat{R}_A(\mathbf {X},n_t',\mathbf {\mu }) - R_A(\mathbf {X},n_t',\mathbf {\mu }) \bigr ] \nonumber \\&=\varvec{E}_{\mathbf {X}}\bigl [ g_A(\mathbf {X},n_t') - \varvec{E}_{n_t'}A(\mathbf {X}',\mathbf {\mu }) \bigr ]. \end{aligned}$$

(4)

and we expect $bias(f_A)=bias(g_A)=0$.

In the following section we review different measures of accuracy and then show how they are estimated with different $f_A$ and $g_A$ functions. We will see that in practice $f_A(\mathbf {X})$ is defined⁴ as $g_A(\mathbf {X},|\mathbf {X}|)$, so if $g_A$ is biased so will be $f_A$.

3 Measures of evaluation accuracy

As mentioned earlier, we can follow different criteria to quantify how well a test collection is estimating the true system scores. We may compute the absolute error of the mean system scores, the ranking correlation, or even test for statistical significance. In the following subsections we review different measures of the accuracy of an IR test collection.

3.1 Ad hoc measures

These measures are based on the concept of a swap between two systems, that is, according to the observed scores one system is better than another one when, in reality, it is the other way around. Some measures are borrowed or adapted from other fields, such as the Kendall correlation or the Average Precision correlation, while others like sensitivity are specifically defined for IR.

3.1.1 Kendall tau correlation: $\tau$

The Kendall $\tau$ correlation coefficient measures the correlation between the two rankings of $n_s$ systems, computed as the fraction of pairs that are in the same order in both rankings (concordant) minus the fraction that are swapped (discordant):

$$\begin{aligned} \tau =\frac{\#\textit{concordant}-\#\textit{discordant}}{n_s(n_s-1)/2}. \end{aligned}$$

(5)

It thus ranges between $-$1 (reversed ranking) and +1 (same ranking). In Information Retrieval, Kendall $\tau$ is widely used to measure the similarity between the rankings of systems produced by two different evaluation conditions, such as different assessors (Voorhees et al. 1998), effectiveness measures (Kekäläinen 2005), topic sets (Carterette et al. 2009) or pool depths (Sakai and Kando 2008). In our case, we are interested in the correlation between the ranking of systems according to a given collection and the true ranking of systems.

3.1.2 Average precision correlation: $\tau _{AP}$

In Information Retrieval we are often more interested in the top ranked items. For instance, effectiveness measures usually pay more attention to the relevance of the top ranked documents. Similarly, we may tolerate a swap between systems at the bottom of the ranking, but not between the two best systems. Yilmaz et al. (2008) proposed an extension of Kendall $\tau$ to add this top-heaviness component following the rationale behind Average Precision. Instead of comparing every system with all others, it only compares it with those ranked above it:

$$\begin{aligned} \tau _{AP}=\frac{2}{n_s-1}\sum _{s=2}^{n_s}\left( \frac{C(s)}{s-1}\right) -1, \end{aligned}$$

(6)

where C(s) is the number of systems above rank s correctly ranked with respect to the system at that rank. Note that $\tau _{AP}$ similarly ranges between $-$1 and +1, but it penalizes swaps towards the top of the ranking more than towards the bottom, making it a more appealing alternative for IR evaluation.

3.1.3 Absolute and relative sensitivity: $sens_{abs}$ and $sens_{rel}$

If the observed difference between two systems is large, it is unlikely that their true difference has a different sign, because the likelihood of a swap is inversely proportional to the magnitude of the difference. Therefore, another view of accuracy is establishing a threshold such that if the observed difference between two systems is larger, the probability of actually having a swap is kept below some level like 5 % (Voorhees and Buckley 2002; Buckley and Voorhees 2000). Of course, we want that threshold to be as small as possible, meaning that we can trust the sign of most of the observed differences. The smallest threshold that ensures a maximum swap rate is called the sensitivity of the collection.

Sanderson and Zobel (2005) pointed out that differences between systems are often reported in relative terms rather than absolute (e.g. +12 % instead of +0.032), so we may also be interested in the relative sensitivity of a test collection. In this paper, we set the maximum swap rate to 5 %, and refer to absolute and relative sensitivity as $sens_{abs}$ and $sens_{rel}$.

3.2 Statistical measures

The ad hoc measures of collection accuracy are concerned with possible swaps between systems, but they neglect the magnitude of their differences as well as their variability. However, the probability of a swap is inversely proportional to the true difference between systems and proportional to their variability: if the observed difference is too small or too variable, they are likely to be swapped. The statistical measures described in the following are all based on the decomposition of the variance of the observed scores. Throughout this section we follow the notation traditionally used in generalizability theory (Brennan 2001; Bodoff and Li 2007).

Because we have a fully crossed experimental design (i.e., all systems evaluated with the same topics), we can consider the following random effects model for the effectiveness of system s on topic t:

$$\begin{aligned} X_{st}=\mu +\nu _s+\nu _t+\nu _{st} , \end{aligned}$$

(7)

where $\mu$ is the grand mean score of all systems in the universe of topics, $\nu _s=\mu _s-\mu$ and $\nu _t=\mu _t-\mu$ are the system and topic effects, and $\nu _{st}$ is the interaction effect that would correspond to the residual effect. Note that a system effect is defined as the deviation of its true mean score $\mu _s$ from the grand average $\mu$, so a system with better (worse) performance than average has a positive (negative) system effect. Topics are defined similarly, that is, a hard (easy) topic has a negative (positive) topic effect. The residual effects just model the system-topic interactions, where some systems are particularly good or bad for certain topics. For each effect in Eq. (7) there is an associated variance of that effect, called the variance component:

$$\begin{aligned} \sigma ^2(s)=\varvec{E}_s\nu _s^2,\quad \sigma ^2(t)=\varvec{E}_t\nu _t^2,\quad \sigma ^2(st)=\varvec{E}_s\varvec{E}_t\nu _{st}^2. \end{aligned}$$

(8)

Because the effects are defined by subtracting the grand mean $\mu$, they are all uncorrelated and centered at zero. Therefore, the total variance of the observed scores can be decomposed into the following components:

$$\begin{aligned} \sigma ^2(X_{st})=\varvec{E}_s\varvec{E}_t(X_{st}-\mu )^2=\sigma ^2(s)+\sigma ^2(t)+\sigma ^2(st). \end{aligned}$$

(9)

Note that this total variance is the variance for single systems on single topics. However, researchers compare systems based on their mean performance over the sample of topics in a test collection. The linear model for the decomposition of a system’s average score over a sample of topics is

$$\begin{aligned} X_{sT}=\overline{X}_{s}=\mu +\nu _s+\nu _T+\nu _{sT}, \end{aligned}$$

(10)

which is analogous to Eq. (7) except that the index of a topic t is replaced by T to indicate the mean over a set of topics. From the above model, we can see that the true mean score of a system s is the expected value, over randomly parallel sets of topics, of the observed mean scores:

$$\begin{aligned} \mu _s=\varvec{E}_T X_{sT}. \end{aligned}$$

(11)

Because the $\nu _T$ and $\nu _{sT}$ effects involve the mean over a set of $n_t$ independent topics from the same universe, their corresponding variance components are

$$\begin{aligned} \sigma ^2(T)=\varvec{E}_T\nu _T^2=\frac{\sigma ^2(t)}{n_t},\quad \sigma ^2(sT)=\varvec{E}_s\varvec{E}_T\nu _{sT}^2=\frac{\sigma ^2(st)}{n_t}, \end{aligned}$$

(12)

and as in Eq. (9), the variance of the observed mean scores is decomposed into

$$\begin{aligned} \sigma ^2(X_{sT})=\varvec{E}_s\varvec{E}_T(X_{sT}-\mu )^2=\sigma ^2(s)+\sigma ^2(T)+\sigma ^2(sT). \end{aligned}$$

(13)

From Eq. (13) we can see that the variability of the observed mean scores is decomposed into the inherent variability among systems, the variability of the mean topic difficulties, and the variability of the mean system interaction with topics. The following measures of collection accuracy are defined from these components.

3.2.1 Generalizability coefficient: $\text {E}\rho ^2$

Using the above decompositions in variance components, one can define different measures of accuracy based on the concept of correlation. Let Q be true scores of some quantity of interest, such as the true mean effectiveness of systems. A test collection provides us with estimates $\hat{Q}=Q+e$, bearing a certain random and uncorrelated error e. Their correlation is

$$\begin{aligned} \rho (\hat{Q},Q)=\frac{\text {cov}(\hat{Q},Q)}{\sigma (\hat{Q})\sigma (Q)}= \frac{\text {cov}(Q+e,Q)}{\sigma (\hat{Q})\sigma (Q)}= \frac{\sigma ^2(Q)}{\sigma (\hat{Q})\sigma (Q)}= \frac{\sigma (Q)}{\sigma (\hat{Q})}. \end{aligned}$$

(14)

If we take the square of the correlation, this conveniently simplifies to a ratio of variance components:

$$\begin{aligned} \rho ^2(\hat{Q},Q)=\frac{\sigma ^2(Q)}{\sigma ^2(\hat{Q})}= \frac{\sigma ^2(Q)}{\sigma ^2(Q+e)}= \frac{\sigma ^2(Q)}{\sigma ^2(Q)+\sigma ^2(e)}. \end{aligned}$$

(15)

Therefore, one can define a measure of accuracy for some arbitrary quantity of interest as the squared correlation between the true scores and the estimated scores which, in turn, can be easily defined as the variance of the true scores to itself plus error variance (Allen and Yen 1979).

In IR evaluation experiments, we are often interested in the relative differences among systems, that is, in the system deviation scores $\mu _s-\mu$. When using a test collection, we estimate this quantity with $X_{sT}-\mu _T$, so the error of our estimates and its variance are

$$\begin{aligned} \delta _s&=(X_{sT}-\mu _T)-(\mu _s-\mu )=\nu _{sT},\end{aligned}$$

(16)

$$\begin{aligned} \sigma ^2(\delta )&=\sigma ^2(sT). \end{aligned}$$

(17)

Plugging into Eq. (15), we get the following accuracy measure for our estimates of relative system scores (Brennan 2001):

$$\begin{aligned} \text {E}\rho ^2=\rho ^2(X_{sT}-\mu _T,\mu _s-\mu ) = \frac{\sigma ^2(s)}{\sigma ^2(s)+\sigma ^2(sT)}. \end{aligned}$$

(18)

In generalizability theory literature, this measure is called generalizability coefficient. Cronbach et al. (1972) introduced the notation $\text {E}\rho ^2$ to indicate that this coefficient is approximately equal to the expected value, over randomly parallel collections of $n_t$ topics, of the squared correlation between observed and true scores (note that this definition is already concordant with our definition of reliability).

3.2.2 Dependability index: $\varPhi$

Sometimes, a researcher is not interest in the system deviation score $\mu _s-\mu$, but rather in its deviation from a domain-dependent criterion $\lambda$, such as the mean effectiveness of a baseline. In this case, our estimate is $X_{sT}-\lambda$, so the error and its variance are

$$\begin{aligned} \varDelta _s&=(X_{sT}-\lambda )-(\mu _s-\lambda )=X_{sT}-\mu _s=\nu _{T}+\nu _{sT},\end{aligned}$$

(19)

$$\begin{aligned} \sigma ^2(\varDelta )&=\sigma ^2(T)+\sigma ^2(sT). \end{aligned}$$

(20)

Plugging into Eq. (15), we get the following accuracy measure for our criterion-referenced estimates of system performance (Brennan 2001):

$$\begin{aligned} \rho ^2(X_{sT}-\lambda ,\mu _s-\lambda )= \frac{\sigma ^2(\mu _s-\lambda )}{\sigma ^2(\mu _s-\lambda )+\sigma ^2(T)+\sigma ^2(sT)}. \end{aligned}$$

Because the quantity of interest here is the deviation from a fixed criterion $\lambda$, this measure does include the topic effect, which enters the absolute error variance. In the above case of deviation from the observed mean score $\mu _T$, the topic effect did not enter the error variance in Eq. (18) because it is the same for all systems. In the special case when $\lambda =\mu$, this measure is called the dependability index $\varPhi$ (Brennan and Kane 1977):

$$\begin{aligned} \varPhi =\rho ^2(X_{sT}-\mu ,\mu _s-\mu )=\frac{\sigma ^2(s)}{\sigma ^2(s)+\sigma ^2(T)+\sigma ^2(sT)}. \end{aligned}$$

(21)

Intuitively, $\varPhi$ is lower than $\text {E}\rho ^2$ because it involves not only system differences, but also topic difficulties. That is, it involves the estimation of absolute system scores rather than just relative differences among them.

3.2.3 F test

Another view of reliability is given by null hypothesis testing (Hull 1993). In the general case where we compare $n_s$ systems, we may state the null hypothesis whereby all systems have the same true mean scores:

$$\begin{aligned} H_0:\mu _1=\mu _2=\dots =\mu _{n_s}. \end{aligned}$$

After evaluating all systems with a test collection, we may test this hypothesis in search for evidence that at least one of the systems has a different mean from the others. A common test to use here is the F test, which involves a decomposition in variance components as well. In its general form, the F statistic is defined as the ratio of explained variance to residual variance, which in our case is

$$\begin{aligned} F=\frac{\text{explained} \; \text{variance}}{\text{residual} \; \text{variance}}= \frac{\text{between-system} \; \text{variance}}{\text{within-system} \; \text{variance}}. \end{aligned}$$

(22)

The numerator is defined as the between systems mean squares, while the denominator is the within systems or error mean squares. Their definition depends on the variance decomposition. With one-way ANOVA, the experimental design only considers the system effect, so the topic effect is confounded with the error. In two-way ANOVA (equivalent to the above variance decomposition), the experimental design considers both the system and topic effects, so the error mean square is considerably lower (see Sect. 4.2 for details).

Under the null hypothesis, the F statistic in Eq. (22) follows an F distribution parameterized by the degrees of freedom in the numerator and in the denominator. If the observed statistic is larger than the critical value corresponding to those degrees of freedom and a pre-fixed significance level like $\alpha =0.05$, we reject the null hypothesis that all system means are equal, evidencing that at least one of them is different from the others. Under this framework, the accuracy of a collection can be viewed dichotomously: does the F test come up significant or not?

4 Estimation of evaluation accuracy

We could use generic f and g functions to estimate arbitrary measures of accuracy by using a split-half method that extrapolates observations made from previous data. The problem is that the model used to extrapolate, as well as how we make observations from previous data, do not necessarily have a theoretical basis and it might actually end up producing biased estimates. On the other hand, we could derive estimators from statistical theory in search for desirable properties like unbiasedness or low variance. These estimators are easily defined for statistical measures of accuracy because they already incorporate the topic set size in their formulation, but not for ad hoc measures. In the next two sections we review generic split-half estimators for arbitrary measures, and statistical estimators of the statistical measures. In Sect. 4.3 we then propose statistical estimators of the Kendall $\tau$ and $\tau _{AP}$ correlations that, as we will see, behave better than the generic split-half estimators.

4.1 Extrapolation from split-half

A generic estimator found in the literature is based on the extrapolation of the observed accuracy scores over random splits of the available topic set, such as in Zobel (1998), Voorhees et al. (1998, 2009), Voorhees and Buckley (2002), Lin and Hauptmann (2005), Sanderson and Zobel (2005), Urbano et al. (2013a). Let $\mathbf {X}$ be the matrix of effectiveness scores already available to us from an existing collection with $n_t$ topics. The estimator randomly selects two disjoint subsets of n topics each, leading to $\mathbf {X}'$ and $\mathbf {X}''$, and then computes the accuracy $A(\mathbf {X}',\mathbf {X}_T'')$ assuming that the mean scores observed with $\mathbf {X}''$ correspond to the true scores. Running this experiment several times, the mean observed score $\overline{A}$ is taken as an estimate of the expected accuracy of a random set of n topics from the same universe. If we repeat this experiment for subsets of $n=1,2,\dots ,n_t/2$ topics, we can estimate the relation between accuracy and topic set size. Fitting a model to these observed scores, we can extrapolate to the expected accuracy of a collection with an arbitrary number of topics. In particular, we can estimate the expected accuracy of a collection of the same size as our initial collection $\mathbf {X}$. This means that we are actually estimating $\hat{A}(\mathbf {X},\mathbf {\mu })$ as $\hat{R}_A(\mathbf {X},|\mathbf {X}|,\mathbf {\mu })$, that is, we are implicitly setting $f_A(\mathbf {X})=g_A(\mathbf {X},|\mathbf {X}|)$.

The extrapolation error depends on the number of topics we initially have for the splits, the number of trials we run, and the model to interpolate. In this paper, we run a maximum total of 1000 trials for a given initial collection, for topic subsets of at most 20 different and equidistant sizes, and 100 random trials at most for each size. For instance, if we had $n_t=10$ previous topics, we would run 100 random trials at sizes $n=2,3,4,5$, for a total of 400 observations. If we had $n_t=100$ previous topics, we would run 50 random trials of sizes $n=3,6,\dots ,48,50$, for a total of 1,000 observations. Regarding the interpolation model, we test three alternatives:

$$\begin{aligned} \text {exp1:}~~&g_A(\mathbf {X},n_t)=a\cdot n_t^b, \end{aligned}$$

(23)

$$\begin{aligned} \text {exp2:}~~&g_A(\mathbf {X},n_t)=a\cdot \exp (b\cdot n_t), \end{aligned}$$

(24)

$$\begin{aligned} \text {logit:}~~&logit(g_A(\mathbf {X},n_t))=a\cdot \log (n_t)+b, \end{aligned}$$

(25)

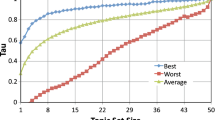
where a and b are the parameters to fit. For exp1 and exp2 we use linear regression on the log-transformed data, and for logit we use generalized linear regression with binomial errors and logit link. Note that these fits are only valid for measures in the range [0, 1]. For $\tau$ and $\tau _{AP}$ we first normalize correlation scores between 0 and 1 prior to model fitting, and then transform the predictions back to the range $[-1,1]$. Figure 2 shows sample split-half estimations of $\tau$ and $sens_{abs}$ based on the initial 50 topics of a TREC test collection.

Fig. 2

Examples of split-half extrapolation of $\tau$ and $sens_{rel}$ scores from the TREC 2004 Genomics collection (Color figure online)

4.2 Inference from ANOVA

The statistical measures are based on theoretical principles that allow us to derive estimators for each statistic of interest. At the top level, we need estimates of each of the variance components from the results of a previous test collection. There are several procedures to estimate variance components, such as maximum likelihood or Bayes, but the most popular is by far the so-called ANOVA procedure (Searle et al. 2006; Brennan 2001). It involves a typical partition of the sums of squares in the observed data, from which we compute the mean squares of each effect. Equating these observed mean squares to their expected values, we obtain the following estimates of the three variance components (Cornfield and Tukey 1956):

$$\begin{aligned} \hat{\sigma }^2(s)&=\frac{MS(s)-MS(st)}{n_t}, \end{aligned}$$

(26)

$$\begin{aligned} \hat{\sigma }^2(t)&=\frac{MS(t)-MS(st)}{n_s}, \end{aligned}$$

(27)

$$\begin{aligned} \hat{\sigma }^2(st)&=MS(st) \end{aligned}$$

(28)

It can be shown that the ANOVA procedure gives best quadratic unbiased estimates without any normality assumptions (Searle et al. 2006). This is important because ANOVA is often said to assume normal distributions, when in reality that assumption is not needed to derive the above estimators; it is the F test following ANOVA the one that makes the assumption. It does assume homoscedasticity and uncorrelated effects, though.

Now that we have estimates of the variance components, we can simply plug them into Eqs. (18) and (21) to estimate the $\text {E}\rho ^2$ and $\varPhi$ scores of a collection of arbitrary size:

$$\begin{aligned} \text {E}\hat{\rho }^2&= \frac{\hat{\sigma }^2(s)}{\hat{\sigma }^2(s) + \hat{\sigma }^2(sT)} = \frac{\hat{\sigma }^2(s)}{\hat{\sigma }^2(s) + \frac{\hat{\sigma }^2(st)}{n_t'}}, \end{aligned}$$

(29)

$$\begin{aligned} \hat{\varPhi }&= \frac{\hat{\sigma }^2(s)}{\hat{\sigma }^2(s) + \hat{\sigma }^2(T) + \hat{\sigma }^2(sT)} = \frac{\hat{\sigma }^2(s)}{\hat{\sigma }^2(s) + \frac{\hat{\sigma }^2(t)+\hat{\sigma }^2(st)}{n_t'}}. \end{aligned}$$

(30)

Intuitively, we can see that the correlations increase when systems are very different from each other to begin with (high $\sigma ^2(s)$) and when systems behave consistently across topics (low $\sigma ^2(t)$ and $\sigma ^2(st)$). If there is too much variability among topics we can increase their number, which will allow us to have even better estimates of system effectiveness. As with the split-half estimators, the above equations are also used to estimate the accuracy of an existing collection as the expected accuracy of a hypothetical collection of the same size. This means that we are again estimating $\hat{A}(\mathbf {X},\mathbf {\mu })$ as $\hat{R}_A(\mathbf {X},|\mathbf {X}|,\mathbf {\mu })$, that is, we are implicitly setting $f_A(\mathbf {X})=g_A(\mathbf {X},|\mathbf {X}|)$.

For the accuracy of a collection in terms of the F test, we can use the above mean squares to compute the F statistic

$$\begin{aligned} F=\frac{MS(s)}{MS(st)}, \end{aligned}$$

(31)

which, under the null hypothesis, follows and F distribution with $n_s-1$ and $n_s(n_t-1)$ degrees of freedom. Intuitively, if the systems are very different from each other (high numerator), or if there is low error variance because systems do not vary too much across topics (low denominator), the F test is more likely to come up statistically significant.

Under the framework of significance testing, the expected accuracy of a test collection corresponds to the statistical power of the test (Webber et al. 2008). In order to estimate the power of a new collection with $n_t'$ topics, we need to specify a target effect size. Sakai (2014a) proposed the use of a minimum detectable difference $\delta _{min}$ between the best and the worst systems, assuming that all other systems are centered in the middle. That is, the best system has an effect $\delta _{min}/2$, the worst system has an effect $-\delta _{min}/2$, and all others have effect 0. This dispersion of the system mean scores results in a between-system variance

$$\begin{aligned} \sigma ^2(s)=\frac{\sum _s\nu _s^2}{n_s}=\frac{(\delta _{min}/2)^2+(-\delta _{min}/2)^2}{n_s}=\frac{\delta _{min}^2}{2n_s} \end{aligned}$$

(32)

which, standardized with the within-system variance, results in the following target effect size for power analysis:

$$\begin{aligned} F_1=\frac{\delta _{min}^2}{2n_s\hat{\sigma }^2(st)}. \end{aligned}$$

(33)

The square root of this effect size is coined $f_1$ by Cohen (1988). We must note that the dispersion of mean system scores assumed above is the one that yields the smallest between-system variance, and hence the one that yields the least statistical power. That is, it assumes the worst case scenario where all but two systems have the same mean, but in practice they spread near uniformly throughout the range. Cohen (1988) defines another two effect sizes assuming intermediate and maximum between-system variance for a given $\delta _{min}$.

For simplicity, we use this effect size in our experiments, but stress again that it contemplates a worst-case scenario that will inevitably underestimate reliability; we leave the topic of appropriate effect size selection for further study. We finally note that the variance decomposition we employ is based on two-way ANOVA because we account for the topic effect as well. This results in a smaller error variance and therefore in higher statistical power than with one-way ANOVA, which confounds the topic and residual effects. In this sense, our estimates are more in line with Sakai (2014b) than with Sakai (2014a).⁵ Following the traditional suggestion by Sparck Jones (1974), we set $\delta _{min}=0.05$ to detect noticeable differences. Note though that this threshold is arbitrary. Urbano and Marrero (2015) recently suggested an approach to define meaningful thresholds based on expectations of user satisfaction, but we leave the choice of thresholds to future research.

4.3 Statistical estimation of Kendall $\tau$ and $\tau _{AP}$

Even though Kendall $\tau$ and $\tau _{AP}$ are two very popular measures in IR evaluation, their split-half estimation for arbitrary topic sets can become computationally expensive for large-scale studies. In addition, as we will see in Sects. 6 and 7, they produce biased estimates. To partially overcome these problems, we propose here two statistical estimators of $\tau$ and $\tau _{AP}$.

For simplicity, let us assume that systems are already sorted by their mean observed score, so that for any two systems i and j, $i<j$ implies $\overline{X}_i>\overline{X}_j$. Let $W_{ij}$ be a random variable that equals 1 if systems i and j are swapped (i.e. $\mu _i<\mu _j$) and 0 if they are not (i.e. $\mu _i>\mu _j$). These variables follow a Bernoulli distribution with parameter $w_{ij}$ equal to the probability of swap, so their expectation and variance are simply

$$\begin{aligned} {\text {E}}[W_{ij}]=w_{ij},\quad {\text {Var}}[W_{ij}]=w_{ij}(1-w_{ij}). \end{aligned}$$

(34)

These probabilities can be estimated with the scores observed in an existing collection. Let $D_t=X_{it}-X_{jt}$ be the difference between both systems for topic t. By the Central Limit Theorem, the sampling distribution of $\overline{D}$ is approximately normal when $n_t$ is large. Therefore, we can estimate $w_{ij}$ as

$$\begin{aligned} w_{ij}=P(\mu _i-\mu _j\le 0)\approx \varPhi \left( -\sqrt{n_t'}\frac{\overline{D}}{sd(D)}\right) , \end{aligned}$$

(35)

where $\varPhi$ is the cumulative distribution function of the standard normal distribution. Therefore, an existing collection allows us to estimate the variability of the differences between systems (i.e. sd(D)), which we can use to estimate the probability that systems will be swapped with an arbitrary number of topics $n_t'$.

4.3.1 Expected Kendall $\tau$ correlation: $\text {E}\tau$

The Kendall $\tau$ correlation can be formulated in terms of concordant pairs alone:

$$\begin{aligned} \tau =\frac{\#\textit{concordant}-\#\textit{discordant}}{n(n-1)/2}= \frac{2\cdot \#\textit{concordant}}{n(n-1)/2}-1, \end{aligned}$$

(36)

which for our purposes would be defined as:

$$\begin{aligned} \tau =\frac{4\sum _{i=1}\sum _{j=i+1}{1-W_{ij}}}{n_s(n_s-1)}-1. \end{aligned}$$

(37)

Given a test collection, we can estimate the probability of swap between every pair of systems, so we can estimate the $\tau$ correlation as well. The expectation and variance are

$$\begin{aligned} \text {E}\tau \equiv \text {E}[\tau ]&= \frac{4\sum _{i=1}\sum _{j=i+1}{1-w_{ij}}}{n_s(n_s-1)}-1 ,\end{aligned}$$

(38)

$$\begin{aligned} \text {Var}[\text {E}\tau ]&\approx \frac{16\sum _{i=1}\sum _{j=i+1}{w_{ij}(1-w_{ij})}}{n_s^2(n_s-1)^2}. \end{aligned}$$

(39)

As mentioned above, using Eq. (35) we can easily estimate the probability of swap with an arbitrary number of topics. Thus, Eq. (38) becomes an estimator of the expected $\tau$ correlation when using an arbitrary number of topics, that is, $\varvec{E}_{n_t'}\tau (\mathbf {X}',\mathbf {\mu })$. Additionally, Eq. (39) allows us to compute a confidence interval as well, but this is a line we do not explore in this paper.

4.3.2 Expected AP correlation: $\text {E}\tau _{AP}$

The $\tau _{AP}$ correlation can also be defined in terms of concordant pairs:

$$\begin{aligned} \tau _{AP}=\frac{2}{n_s-1} \sum _{i=2}\left( \frac{\sum _{j=1}^{i-1}1-W_{ij}}{i-1} \right) -1. \end{aligned}$$

(40)

Having a test collection, we can again estimate the probabilities of swap, so we can estimate the $\tau _{AP}$ correlation as well. Expectation and variance are

$$\begin{aligned} \text {E}\tau _{AP}\equiv \text {E}[\tau _{AP}]&=\frac{2}{n_s-1} \sum _{i=2}\left( \frac{\sum _{j=1}^{i-1}1-w_{ij}}{i-1} \right) -1 , \end{aligned}$$

(41)

$$\begin{aligned} \text {Var}[\text {E}\tau _{AP}]&\approx \frac{4}{(n_s-1)^2} \sum _{i=2}\left( \frac{\sum _{j=1}^{i-1}w_{ij}(1-w_{ij})}{(i-1)^2} \right) . \end{aligned}$$

(42)

Similarly, Eq. (41) is an estimator of the expected $\tau _{AP}$ correlation when using an arbitrary number of topics, that is, $\varvec{E}_{n_t'}\tau _{AP}(\mathbf {X}',\mathbf {\mu })$.

5 Stochastic simulation of evaluation results

In order to evaluate the possible bias of each $\hat{A}$ and $\hat{R}$, we need to be able to compute the true $A(\mathbf {X},\mathbf {\mu })$ scores, which means that we need to know the true effectiveness of systems. For instance, to assess the possible bias of the exp1 split-half estimator of the $\tau$ correlation coefficient, we actually need to compute the correlation between the true ranking of systems and the ranking produced by a test collection. In principle, we thus need to know the true effectiveness of systems and a way to obtain randomly parallel test collections of varying sizes where topics are sampled from the same universe of topics. Finally, we also want to be able to control which statistical assumptions are violated in the creation of these test collections, so we can assess the robustness of the estimators to each of these violations. Unfortunately, there is no way of knowing the true effectiveness of systems, certain assumptions are not met by definition, and there is no archive of past evaluation data large enough to serve our needs. Instead, we resort to stochastic simulation.

Let $\mathbf {X}$ be the $n_t\times n_s$ matrix of effectiveness scores obtained by a set of systems with an existing set of topics. Our goal is to simulate a new matrix $\mathbf {Y}$ with scores by the same set of systems with a randomly parallel set of $n_t'$ topics. The complexity of course resides in making this simulation realistic. There are four main points we must consider:

• We need to know the exact true mean scores of systems $\mathbf {\mu }$, each of which must equal $X_{sT}$ in expectation: $\mu _s=\varvec{E}_{T}X_{sT}$, which implies $\mu =\varvec{E}_{T}\varvec{E}_s X_{sT}$. This will allow us to compute the actual accuracy of the simulated collections.

• Regardless of the assumptions, topic effects must be sampled from a fixed true distribution of the universe of topics.

• The dependence structure underlying topic and residual effects must be preserved to maintain the possible correlations between systems and topics (see the bottom plots in Fig. 1). This will allow us to preserve the inherent similarity between systems by the same group, or the interaction between systems and topic difficulty, for example.

• Even though the residual distributions can sometimes be approximated by certain families of well-known distributions, we need to adhere to their true distributions, especially when we do not want the homoscedasticity or normality assumptions to hold.

One could just set one Beta distribution for each system and draw random variables, but the resulting residuals would not necessarily follow the realistic distributions. Even if one estimates each residual distribution and draws samples from those estimates, the expected topic effects would all be zero. If one also estimates the topic effect distribution and draws from it as well, the dependence structure would still be ignored. In the next section we outline the method we follow to simulate realistic evaluation results.

5.1 Outline of the simulation method

Algorithm 1 details the full simulation method. For the time being, let us describe it without paying attention to how statistical assumptions are dealt with; they will be covered in Sect. 5.2. We begin by considering again the model in Eq. (7) to decompose effects in the existing collection. For our purposes, we will fix the true grand average and the true system effects as the observed mean scores in $\mathbf {X}$ (lines 5–6):

$$\begin{aligned} \mu&\equiv \overline{X}_{st}=\frac{1}{n_sn_t}\sum _s{\sum _t{X_{st}}},\end{aligned}$$

(43)

$$\begin{aligned} \nu _s=\mu _s-\mu&\equiv \overline{X}_s-\mu =\frac{1}{n_t}\sum _t{X_{st}}-\mu \end{aligned}$$

(44)

Fixing $\mu$ and $\nu _s$ allows us to compute the actual accuracy of a simulated randomly parallel collection $\mathbf {Y}$. The following mixed effects model will serve as the basis to simulate such collection

$$\begin{aligned} Y_{st}=\mu +\nu _s+T_t+E_{st}, \end{aligned}$$

(45)

where $T_t$ and $E_{st}$ are random variables corresponding to the topic and residual effects. Let $F_T$ be the true cumulative distribution function of topic effects, let $F_{E_s}$ be the true cumulative distribution function of residual effects for system s, and let $F_T^{-1}$ and $F_{E_s}^{-1}$ be their inverses (i.e., the quantile functions). Under this model, each topic t corresponds to a random vector $(E_{1t},\dots ,E_{n_st},T_t)$ from a joint multivariate distribution F whose marginal distributions are $(F_{E_1},\dots ,F_{E_{n_s}},F_T)$. The simulation mainly consists in generating such random vectors and plugging them in Eq. (45).

If we just drew independent random variables from the distributions of topics and residuals, we would lose their inherent correlations. To avoid this, we use copulas. A copula is a multivariate distribution that describes the dependence between random variables whose marginals are all uniform. By Sklar’s theorem, any joint multivariate distribution, like our F distribution, can be defined in terms of its marginal distributions and a copula describing their dependence structure (Joe 2014). Copulas are used as follows. Let $(A_1,A_2,\dots )$ be a random vector where each variable follows some distribution $F_{A_i}$. By the probability integral transform, if we pass each of them through their distribution function, we get a random vector where the marginals are uniform: $U_i=F_{A_i}(A_i)\sim \text {Uniform}(0,1)$. Now, let C be the copula of the multivariate distribution of $(U_1,U_2,\dots )$; it contains the dependence structure between all $U_i$ and its marginals are all uniform. We can now use the copula to generate a random vector $(R_1,R_2,\dots )$, which maintains the dependence structure and can be transformed back to our original distribution. In particular, we now compute $A_i'=F_{A_i}^{-1}(R_i)$ to obtain a random vector with the same marginals: $A_i'\sim F_{A_i}$.

There are many families of copulas to model different types of dependence structure. Here we will use Gaussian copulas because they are easy to work with and they maintain the correlation between variables. First, we use kernel density estimation to estimate and fix the true marginals of the topic and residual effects; let $\hat{F}_T$ and $\hat{F}_{E_s}$ be our estimates (lines 11–12). Now, we need to generate $n_t'$ random vectors from a Gaussian copula with the same variance-covariance matrix as our topic and residual effects (note from line 13 that topic effects are appended to residual effects). We achieve this by generating independent standard normal vectors and multiplying them by the Cholesky factorization of the variance-covariance matrix $\hat{\mathbf {\Sigma }}$ (lines 13, 22–24). Next, we pass each of the resulting $\mathbf {R}_s$ vectors through the normal cumulative distribution function $\varPhi$ with mean 0 and variance $\hat{\Sigma }_{s,s}$, which results in the uniform random vectors generated from the copula (line 25).

These random vectors have the desired correlations, but not the marginals yet, so we pass each of them through the inverse distribution function of the corresponding residual or topic effect (line 29). Each of the resulting variables $Z_{st} (s\le n_s)$ corresponds to the residual effect of system s for the new topic t, and the $Z_{n_s+1,t}$ are the new topic effects. The simulated score $Y_{st}$ of system s for topic t is computed by adding these two random effects to the fixed grand mean $\mu$ and the fixed true system effect $\nu _s$ (line 33).

5.2 Dealing with statistical assumptions

The basic algorithm presented so far allows us to simulate the effectiveness scores obtained by a certain set of systems on an arbitrarily large set of topics from the same universe. In this section we describe how this basic algorithm is expanded to simulate data following various combinations of statistical assumptions.

Normality In line 29 of the algorithm, we pass each of the random vectors generated with the copula through the inverse distribution functions of the residual and topic effects, so the marginals are the same as in our original data. If we want to force the normality assumption, all we have to do is substitute all $\hat{F}_{E_s}$ (and their inverses) with the normal distribution function with mean 0 and variance $\hat{\Sigma }_{s,s}$, so the resulting residuals are all normal and with the original variance (lines 26–28). Note that the transformation of the topic effects is still done with $\hat{F}_T^{-1}$, because the normality assumption applies only to the residuals. If, on the other hand, we do not force the normality assumption, the residuals will have the correct marginals, but the actual scores may fall outside the [0, 1] range when adding all effects, resulting in unrealistic data. To avoid this, we first transform the original scores $\mathbf {X}$ with the logit function, so the range becomes $(-\infty ,+\infty )$ instead of [0, 1] (lines 2–4). The algorithm proceeds the same way to generate the new data $\mathbf {Y}$ in logit units, and the inverse logit function is used at the end to transform the simulated scores back to the [0, 1] range (lines 34–36). Through appropriate transformation, we can thus simulate data with residuals following normal distributions or realistic distributions as in the original data.

Homoscedasticity Because we use the variance-covariance matrix of the original data throughout the algorithm, the simulated scores have the same within-system variance as in the original data. This implies that if the original data is heteroscedastic, the simulated data will be heteroscedastic too. If we want to force homoscedasticity, we can re-scale all the residuals to have a common (pooled) variance $\sigma ^2_p$ (lines 7–10). Note that the transformed residuals are still centered at zero, and the correlations among residual and topic effects do not change because this transformation is linear.

Fig. 3

Sample Beta distributions used for non-random sampling of topic effects; they define the probability that certain quantiles of the topic effects distribution will be sampled. For instance, with $\alpha =0.01$ and $\beta =8$ (solid green line) we are most likely to select topics from the lower quantiles, that is, harder topics. A uniform distribution (dashed gray line) would achieve random sampling (Color figure online)

Uncorrelated effects The use of copulas in the algorithm is motivated by the observation that IR evaluation scores do present a certain level of correlation that we want to preserve. If we still want to force uncorrelated effects we can simply set all the off-diagonal components of the variance-covariance matrix to zero, so that we maintain the residual variances but not their correlations (lines 14–16). An alternative is to just generate and transform independent normal random variables with the appropriate variances instead of using the copula, but we prefer to modify the variance-covariance matrix for simplicity.

Random sampling The simulated topic effects are sampled uniformly from the fixed $\hat{F}_T$ distribution, so the simulated data assumes random sampling by default. If we want to force non-random sampling, we can just simulate data for many more topics, say, four times as many (lines 17–21), and by the end of the algorithm sample non-uniformly from them (lines 30–32). From line 29, our simulated $n_t''$ topic effects are in vector $\mathbf {Z}_{n_s+1}$. The objective is to select a non-random sample of $n_t'$ such topic effects and their corresponding residuals. To do so, we generate $n_t''$ random variables from a skewed Beta distribution, which will represent different quantiles of the empirical topic effects distribution. Our final sample will contain the topics at those quantiles. The shape parameters $\alpha$ and $\beta$ of the Beta distribution are randomly chosen from [0.01, 2] and [2, 8], and swapped randomly as well. Figure 3 shows examples of Beta distributions with the extreme combinations of shape parameters. Recall though that the figure only shows the most extreme Beta distributions; we actually sample using random shape parameters within the pre-fixed intervals.

5.3 Data

In principle, the stochastic simulation algorithm can be applied to an arbitrary previous collection given that all systems are evaluated with the same topics. To assess how realistic the simulated evaluation scores are, we use four representative TREC test collections. Note that for our purposes we are interested in collections that are representative in terms of score distributions, not in terms of task or retrieval techniques. In particular, we are interested in how difficult they are to evaluate, as opposed to how difficult the task is.

A brief analysis of over 45 past TREC test collections, reveals that the average variance components across collections are σ ²(s) = 7 %, σ ²(t) = 57 % and σ ²(st) = 36 % and , with $n_s=49$ systems on average. Based on this, we selected three collections with small, intermediate and large system effects, each representing various levels of difficulty, and a fourth collection of intermediate difficulty but with an effectiveness measure whose score distributions diverge largely from a normal distribution. As Table 1 shows, the selected test collections are from the Enterprise 2006 expert search, Genomics 2004 ad hoc search, Robust 2003, and Web 2004 collections. In order to avoid possibly buggy system implementations, we drop the bottom 25 % of systems from each collection, as done in previous studies such as Voorhees and Buckley (2002), Sanderson and Zobel (2005), Bodoff and Li (2007), Voorhees et al. (2009), and Urbano et al. (2013b).

Table 1 Summary of the four TREC test collections used in the paper

For each of the four initial collections we ran 100 random trials of the simulation algorithm for each of the 16 combinations of statistical assumptions (normality, homoscedasticity, uncorrelated effects and random sampling), and for target topic sets of $n_t'=$ 5, 10, 15, 20, 25, 35, 50, 100, 150, 200, 250, 350 and 500 topics. Therefore, the results presented in this paper comprise 20,800 simulations for each original test collection and a total of 83,200 overall.

5.4 Results

In order to diagnose the simulations, we use several indicators to compare every simulated collection with its original one under different criteria. In this analysis we do not include simulated collections of 5 and 10 topics because they are highly unstable to begin with.

5.4.1 Quality of the simulations

The first indicator measures the deviation of the observed mean scores of systems with respect to their true mean scores: $\varvec{E}_s(\hat{\mu }_s-\mu _s)=\varvec{E}_s(X_{sT}-\mu _s)$. For instance, if the deviation is positive it means that the effectiveness of systems is larger than it should; as mentioned before, this deviation should be zero in expectation. The top-left plot in Fig. 4 shows the distributions of deviations for each original collection and when the random sampling assumption holds or not. As expected, we see that the deviation is near zero in all cases, meaning that the mean system scores are unbiased. We can see that single deviations are much more variable in the absence of random sampling, because individual collections contain a biased sample of topics that biases the mean system scores. The middle-left plot shows deviations as a function of the number of topics in the simulated collection. We can see that not only is the mean deviation zero, but also that it is less and less variable as we increase the collection size. This evidences that larger collections are more reliable to estimate the true system scores. Finally, because larger collections ensure smaller deviations, we should observe in general that the estimated rankings of systems are closer to the true ranking. The bottom-left plot confirms that the $\tau _{AP}$ correlations between the simulated and the original collections do indeed increase with the topic set size. As expected, correlations are higher under random sampling.

Fig. 4

Distributions of first diagnosis indicators: deviation between observed and true system scores (left, top and middle), $\tau _{AP}$ correlations (left, bottom), distance between observed and original distributions of topic effects (right, top and middle), and distance between observed and original distributions of residuals (right, bottom) (Color figure online)

Even though the mean system scores are unbiased, it is still possible that the distributions differ largely from the original ones, so the next indicators compare the topic and residual distributions. In particular, we compute the Cramér-von Mises $\omega ^2$ distance (Cramér 1928; von Mises 1931) between the true distributions in the original collection and the distributions observed in each simulated collection; let F be the one from the original and $\hat{F}$ be the corresponding one from the simulation. The distance can be estimated from the empirical distributions as

$$\begin{aligned} \hat{\omega }^2=\frac{1}{n}\sum _i (\hat{F}(i)-F(i))^2, \end{aligned}$$

where i iterates the n scores in the larger collection, original or simulated. The top-right plot in Fig. 4 shows the distributions of $\hat{\omega }^2$ distances in the topic effect distributions, for each original collection and under random sampling or not. We can observe that the distributions of topic effects in the simulations are fairly similar to the originals (small distances), and that non-random sampling produces more different distributions. In the middle-right plot we can see that the distributions get steadily closer to the originals as the number of topics increases. Finally, in the bottom-right plot we show the distance between the distributions of residuals, and similarly observe that they get closer to the originals as we increase the number of topics, and that they are also closer under random sampling.

Fig. 5

Distributions of second diagnosis indicators: deviation between observed and true variance of the system, topic and system-topic interaction effects (left), deviation in the variability of system residual variances (right, top and middle), and correlation between correlation matrices in the simulated and original collections (right, bottom) (Color figure online)

Another aspect of interest is the percentage of total variance due to the system, topic, and system-topic interaction effects ($\sigma ^2(s)$, $\sigma ^2(t)$ and $\sigma ^2(st)$). These values should be preserved in the simulated collections except with non-random sampling, which biases the distribution of topic effects and, by extension, the contribution to total variance of the system and system-topic interaction effects. We similarly compute a deviation score like $\hat{\sigma }^2(s)-\sigma ^2(s)$ between the simulation and the original. For instance, a positive deviation in the system variance component would mean that systems are farther apart in the simulation than in the original. The three left plots in Fig. 5 show these deviations for all three components and for each original collection. When random sampling is in place the deviations are all very close to zero. When random sampling is not assumed the topic effect is larger in the original collection (negative deviation) because it uniformly covers the full support of the true topic effect distribution, while the simulated collections are skewed towards low or high quantiles (compare for instance the blue and gray distributions in Fig. 3). In turn, the system and system-topic interaction effects are larger in the simulated collections (positive deviations).

Yet another indicator of interest is the variability in the distribution of residual variances: $sd(\varvec{E}_s\sigma ^2(\nu _{st}))$. Under the homoscedasticity assumption, this standard deviation should be zero because the variances of the system residuals are all the same. With heteroscedasticity we should observe a non-zero standard deviation because the variances of the residuals are not necessarily the same. In this case we also compute a deviation score between a simulated collection and its corresponding original collection. The top-right plot show that when heteroscedasticity is present the deviations are nearly zero, meaning that the variability of the variances is virtually the same as in the original collection. When homoscedasticity is assumed, the variability of variances is smaller in the simulated collections (negative deviation), as expected. The center-right plot shows that the indicator deviations need a certain number of topics to converge because small collections are unstable and the indicators are too variable. Here we can similarly observe that under heteroscedasticity the convergence is at zero, and under homoscedasticity it is at a negative quantity.

The final indicator is the correlation among residual effects in the simulation and the effects in the original collection. Let $\Sigma$ be the correlation matrix among residuals in the original collection, and $\hat{\Sigma }$ among residuals in the simulation. The indicator is itself the correlation between the off-diagonal components of these matrices, that is, how well the correlations among effects are preserved in the simulated collection. The bottom-right plot shows that when we assume uncorrelated effects the correlation is indeed nearly zero, meaning that no dependence is preserved among systems. When correlated effects are assumed, the indicator approaches one because the correlation matrices are very similar between the simulation and the original collections.

5.4.2 Robustness of the simulation algorithm

In order to confirm what factors affect the quality of the simulations, and to what extent, we next perform a variance decomposition analysis to see how much of the variability of each indicator is due to each of the main factors. If a factor has a large effect it means that the indicator varies too much across the different levels of the factor. For instance, if the topic set size has a large effect on the $\tau _{AP}$ indicator, it means that there is a large difference in $\tau _{AP}$ across topic set sizes. Similarly, if the homoscedasticity assumption has a negligible effect, it means that the $\tau _{AP}$ scores do not vary depending on whether we assume homoscedasticity or not. The overall correlations may be large or small, but they do not depend on the homoscedasticity assumption.

Table 2 lists the results of the variance decomposition analysis for each indicator. The first column shows that virtually all the variability in the $\mu _s$ indicator falls under the residual effect. This residual effect merges the variation across the 100 random trials of the simulation algorithm for each condition, as well as the interactions among factors, which were not fitted. What the table tells us is that none of the main effects has a relevant effect on the deviation of the $\mu _s$ scores, so the mean of the deviations remains the same regardless of the original collection, topic set size, etc. This was already suggested in Fig. 4, because the mean deviations were all around zero. The second column shows that both the original collection to simulate from and the number of topics to simulate, affect the correlation. This is expected because difficult collections need many topics to produce accurate estimates and high correlations with the original ranking.

Table 2 Variance decomposition analysis of the distributions of simulation diagnostic indicators

The third column shows that the similarity between the topic effect distributions is affected by whether random sampling is in place or not: as we saw, non-random collections differ more than the random ones. The fourth column shows that the similarity between the system residual distributions is also affected by the random sampling assumption, but also by the normality assumption and the number of topics to simulate. This is also expected, as the normality assumption directly transforms the residual distributions. The fifth to seventh columns show that the system, topic and system-topic variance components are only affected by the random sampling assumption, as we saw in Fig. 5. The second to last column shows that the homoscedasticity assumption has the largest effect on the variability of residual variances, followed by the topic set size and the particular original collection (the degree to which it is heteroscedastic itself). Finally, we see that virtually all the variability in the correlation indicator is in fact due to the uncorrelated effects assumption.

In summary, the diagnosis results confirm that the proposed algorithm for stochastic simulation of evaluation results produces realistic effectiveness scores and behaves as expected under the combination of statistical assumptions in place. In addition, we have seen that it is robust to the characteristics of the original collection to simulate from.

6 Accuracy of an existing test collection

Here we consider the first scenario where an IR researcher has an existing test collection with $n_t$ topics and wants to estimate its accuracy. In particular, we are interested in how well our $\hat{A}(\mathbf {X},\mathbf {\mu })$ estimates of accuracy reflect the true accuracy of the collection. To this end, we compute the bias of our estimates as in Eq. (3). Recall that in this study we can compute the actual accuracy scores because, thanks to the simulation algorithm, the true system scores are fixed and known. First, we evaluate the bias of the estimators in the arguably most realistic scenario of non-normal distributions, heteroscedasticity, correlated effects and random sampling. Second, we evaluate how robust they are to these assumptions.

6.1 Bias of the accuracy estimates

For each measure of accuracy, we take the 100 randomly simulated collections for each of the 13 topic set sizes, but only under non-normal distributions, heteroscedasticity, correlated effects and random sampling. This makes a total of 1300 datapoints for each original TREC collection and 5200 overall for each measure.

The top plots in Fig. 6 show the bias in the estimates of the Kendall $\tau$ correlation of the simulated collections. We can observe that the exp1 and logit models are extremely similar [the log transformation of Eq. (23) is actually very similar to Eq. (25)], and that both of them consistently underestimate the true $\tau$ scores of the collections (negative bias). On the other hand, the exp2 model underestimates the correlation for small collections and overestimates it for large collections, apparently converging to a constant positive bias. These behaviors are consistent with Fig. 2. Finally, $\text {E}\tau$ also overestimates the true correlations, but less so than the other estimators. Even though the estimation error is still large for small topic sets, we can see that for a realistic collection of 50 or more topics the estimation error is negligible. The bottom plots in Fig. 6 show remarkably similar trends for the $\tau _{AP}$ correlation, where the proposed $\text {E}\tau _{AP}$ estimator behaves better than the split-half estimators again. In all cases we can see that the estimators are less biased with the Enterprise collections than with the Robust collections, most likely because the former are easier for evaluation due to the high system effect variance.

Fig. 6

Bias of the estimators of $\tau$ (top) and $\tau _{AP}$ (bottom) scores for the simulated collections originating from each TREC collection. The plots only show simulated collections under realistic statistical assumptions (Color figure online)

Figure 7 similarly shows the bias of the absolute (top plots) and relative sensitivity (bottom) estimators. Both exp1 and logit tend to overestimate the actual sensitivity of the collections, therefore underestimating their accuracy. The pattern is again consistent with Fig. 2: exp2 gives lower estimates than logit, which gives lower estimates than exp1. As expected, split-half estimates of sensitivity are less accurate than estimates of correlation because they involve not only for the signs of system differences, but also for their magnitudes (in addition, recall that correlations range between $-$1 and +1, while sensitivity ranges between 0 and 1). Nonetheless, the exp2 estimates are very close to the actual values for collections with a realistic number of topics.

Fig. 7

Bias of the estimators of $sens_{abs}$ (top) and $sens_{rel}$ (bottom) scores for the simulated collections originating from each TREC collection. The plots only show simulated collections under realistic statistical assumptions (Color figure online)

Figure 8 shows the bias of the $\text {E}\rho ^2$ (top plots) and $\varPhi$ (middle) estimates. Unlike in the previous measures, estimates of $\text {E}\rho ^2$ tend to underestimate accuracy, even though for large collections it provides fairly good estimates. While $\varPhi$ is similarly underestimated, bias is generally larger, especially in the difficult Robust collections where the topic effect is large. This is consistent with generalizability theory literate stating that Eqs. (29) and (30) in fact biased (Webb et al. 2006). The bottom plots of the same figure show the bias of the F measure (recall that this is actually the power of the F test). We note that the actual power in the Enterprise collections is always 1 because there is a large between-system variance; in the other cases, and especially in the Robust collection, several dozen topics are needed for the F tests to come up significant. We can see that the $F_1$ estimator has a very clear bias, highly underestimating the accuracy of test collections. As a result, it suggests the use of many more topics than actually needed to achieve a certain level of power in the F test. This behavior is consistent with our comments in Sect. 4.2. In particular, it evidences that the use of the $F_1$ effect size can be misleading. It is defined from a minimum detectable difference $\delta _{min}$ between the best and worst systems, and the power analysis tells us how many topics we need to detect that difference. However, if the true difference between the best and worst systems is larger than $\delta _{min}$ to begin with, as is in our collections, the accuracy of the collection is systematically underestimated.

Fig. 8

Bias of the estimators of $\text {E}\rho ^2$ (top), $\varPhi$ (middle) and F (bottom) scores for the simulated collections originating from each TREC collection. The plots only show simulated collections under realistic statistical assumptions (Color figure online)

6.2 Robustness to statistical assumptions

The previous section showed the bias of the estimators in the arguably most realistic scenario of non-normal distributions, heteroscedasticity, correlated effects and random sampling. We now study their robustness to these statistical assumptions, taking the full set of 83,200 simulated collections. In particular, for each estimator we run again a variance decomposition analysis over the distribution of estimation errors, thus showing how much of the variability in the estimation error is attributable to each assumption, the topic set size, and the original TREC collection. This allows us to detect effects that influence the estimation errors.

Table 3 shows the variance components for the $\tau$ and $\tau _{AP}$ measures. In the case of the split-half estimators, we see that the largest non-residual effect is the topic set size, confirming our previous observation that estimates with a handful of topics are very unstable to begin with. On the other hand, our proposed $\text {E}\tau$ and $\text {E}\tau _{AP}$ estimators are significantly more robust to the topic set size, meaning that they can generally be trusted even for small collections. They are also more robust in general, as shown by the smaller total error variance. This means that they are not only less biased, but also more stable. All estimators are slightly affected by the uncorrelated effects assumption, probably because swaps among systems are not independent of each other (eg. a swap between the third and sixth systems probably implies a swap between the third and the fourth as well). As expected, the normality and homoscedasticity assumptions do not affect the estimators, although they are all affected to some degree by the random sampling assumption. In any case, we note that the random sampling assumption has an effect as important as the topic set size or even the original collection itself.

Table 3 Variance decomposition of the error of the $\tau$ and $\tau _{AP}$ estimates of an existing collection

Table 4 shows the results of a similar analysis for the $sens_{abs}$ and $sens_{rel}$ measures. The first difference we notice is that absolute sensitivity has smaller error variance and is therefore more robust in general. The exp1 estimators are the most clearly affected by the topic set size, as evidenced in Fig. 7 as well. The uncorrelated effects and random sampling assumptions appear to affect the estimators as well, though most of the observed variability in the estimation errors falls under the residual effect, especially for the exp2 and logit estimators. The normality and homoscedasticity assumptions do not affect the estimates.

Table 4 Variance decomposition of the error of the $sens_{abs}$ and $sens_{rel}$ estimates of an existing collection

Table 5 similarly shows the results for the $\text {E}\rho ^2$ and $\varPhi$ measures. We can see that both measures are slightly affected by the topic set size, but the largest non-residual source of variability is the random sampling assumption. Its effect is remarkably large in $\varPhi$ because, unlike $\text {E}\rho ^2$ it estimates the topic difficulties, which can vary considerably with non-random samples (see Sect. 5.4). The table also lists the results for the F test measure, showing that its accuracy depends on the collection (actually, on the ratio of system-variance to topic-variance), and certainly on the number of topics in the collection. As evidenced by Fig. 8, the $F_1$ estimator is quite unreliable. The normality and homoscedasticity assumptions do no affect.

Table 5 Variance decomposition of the error of $\text {E}\rho ^2$, $\varPhi$ and F estimates of an existing collection

7 Expected accuracy of a hypothetical test collection (reliability)

Here we consider the second scenario where an IR researcher has access to an existing collection with $n_t$ topics and wants to estimate the expected accuracy of a hypothetical collection with $n_t'$ topics from the same universe. This scenario is present for instance when deciding whether to spend resources in judging more topics for an existing collection. In particular, we are interested in how well our $\hat{R}(\mathbf {X},n_t',\mathbf {\mu })$ estimates of reliability reflect the true reliability of a topic set size $n_t'$. To this end, we compute the bias of our estimates as in Eq. (4). Recall again that in this study we can compute the true reliability scores because we know the true system scores. As before, we first evaluate the bias of the reliability estimates in the arguably most realistic scenario of non-normal distributions, heteroscedasticity, correlated effects and random sampling. After that, we evaluate how robust each estimator is to these assumptions.

7.1 Bias of the reliability estimates

For each measure of accuracy, we take the 100 randomly simulated collections for each of the 13 topic set sizes $n_t$, but only for the case of non-normal distributions, heteroscedasticity, correlated effects and random sampling. For each of these we compute the 13 estimates of the reliability of new topic set sizes $n_t'$, and compare the estimates with the actual accuracy observed with sizes $n_t'$. This is done for each original collection separately, and then all bias scores are averaged across them. This makes a total of 16,900 datapoints for each original TREC collection and 67,600 overall for each measure.

Figure 9 shows the bias of the estimates of $\tau$ (top plots) and $\tau _{AP}$ (bottom) reliability. For simplicity, we only show the estimates from existing collections of $n_t=$ 5, 10, 20, 50, 100 and 200 topics; the trends are evident from the figures. The first difference we can see is that exp2, which showed good behavior to estimate the accuracy of an existing collection, is very erratic to estimate the expected accuracy of a new collection. This is because of the observed behavior that exp2 is not consistent: it underestimates accuracy until a certain number of topics is reached, beyond where it starts overestimating. Since we are now extrapolating to different topic set sizes $n_t'$, this behavior becomes problematic. As the number of existing topics $n_t$ increases, the exp1 and logit estimators get closer to the estimates of accuracy from the previous section, where $n_t=n_t'$ (dashed black line). The extrapolations to large topic sets are quite good provided that we have about 100 topics to begin with, which is hardly ever the case. With smaller existing collections, both exp1 and logit highly underestimate the expected correlations of large collections. The proposed $\text {E}\tau$ and $\text {E}\tau _{AP}$ show significantly better performance. In fact, with as little as $n_t=20$ initial topics the predictions are very good. More importantly, we can see that the estimators are consistent and, unlike the split-half estimators, they get closer to the true values as the initial number of topics increases.

Fig. 9

Bias of the estimators of $\tau$ (top) and $\tau _{AP}$ (bottom) of a new collection with $n_t'$ topics, given an existing collection with $n_t$ topics. The plots only show simulated collections under realistic statistical assumptions (Color figure online)

Figure 10 similarly shows the bias of the absolute (top plots) and relative sensitivity (bottom) reliability estimates. The exp2 estimator shows again very erratic behavior, especially for small target topic set sizes. On the other hand, the logit estimator shows very good performance; with as little as $n_t=20$ initial topics it provides close estimates of the reliability of larger collections. In the case of exp1, the convergence is slower; it requires about 50 initial topics for $sens_{abs}$ and about 100 for $sens_{rel}$. Once again, we appreciate that these split-half estimators also estimate the expected (biased) estimate of accuracy instead of the expected (true) accuracy of a larger collection.

Fig. 10

Bias of the estimators of $sens_{abs}$ (top) and $sens_{rel}$ (bottom) of a new collection with $n_t'$ topics, given an existing collection with $n_t$ topics. The plots only show simulated collections under realistic statistical assumptions (Color figure online)

Figure 11 shows the bias of the $\text {E}\rho ^2$ and $\varPhi$ reliability estimates. We can observe that reliability is generally underestimated. Large initial collections provide better estimates of new collections, but around $n_t=20$ initial topics seem sufficient to have good estimates. These results agree with Urbano et al. (2013b), who analyzed the effect of the initial collection size on the estimates of the required number of topics to reach a certain level of reliability. As expected by its poor performance in the previous section, the $F_1$ estimator consistently underestimates the power of the F test, regardless of the number of topics in the initial collection.

Fig. 11

Bias of the estimators of $\text {E}\rho ^2$, $\varPhi$ and F of a new collection with $n_t'$ topics, given an existing collection with $n_t$ topics. The plots only show simulated collections under realistic statistical assumptions (Color figure online)

7.2 Robustness to statistical assumptions

In the previous section we evaluated the bias of the reliability estimators in the scenario of non-normal distributions, heteroscedasticity, correlated effects and random sampling. We now study their robustness to these assumptions with the full set of 83,200 simulated collections. In particular, for each estimator we run a variance decomposition analysis over the distribution of estimation errors, showing what fraction of the variability in the estimation error can be attributed to each assumption, the initial $n_t$ and new $n_t'$ topic set sizes, and the original TREC collection. This provides us with a total of 1,081,600 datapoints per measure.

Table 6 shows the results for $\tau$ and $\tau _{AP}$. We can see that most of the variability in the split-half estimators is due to the topic set sizes, either through their main effects ($n_t$ and $n_t'$) or their interaction effect ($n_t:n_t'$). This means that the estimation error depends highly on the number of topics available or under consideration. This is again a direct consequence of the split-half method. On the other hand, the proposed $\text {E}\tau$ and $\text {E}\tau _{AP}$ are not affected by the size of the new collection, and evidence only minor dependence on the size of the existing collection. Indeed, through the total error variance we can see that their estimates clearly outperform the split-half estimators. However, we see a large dependence on the random sampling assumption, and a noticeable dependence on the uncorrelated effects assumption. The normality and homoscedasticity assumptions have negligible effects.

Table 6 Variance decomposition of the estimation error of the expected $\tau$ and $\tau _{AP}$ of a new collection

Table 7 shows similar results for the sensitivity measures. A very large part of the variability in the estimation errors is attributable again to the topic set size effects, evidencing that the accuracy of these estimators depends very much on the size of available data and the size we want to extrapolate to.

Table 7 Variance decomposition of the estimation error of the expected $sens_{abs}$ and $sens_{rel}$ of a new collection

Table 8 shows that the estimation of the expected $\text {E}\rho ^2$ is very slightly affected by the topic set sizes to extrapolate from and to. Recall that this does not mean that the estimates are good across sizes, but that the estimation error remains the same across sizes. It also shows some dependence on the uncorrelated effects assumption, but most of the variability in the estimation errors is due to the random sampling assumption. This is where almost 90 % of the variability in $\varPhi$ comes from, evidencing stability problems if this assumption is not guaranteed. In the case of the $F_1$ estimator, we can clearly see robustness to assumptions, although the estimation errors are highly dependent on the target topic set sizes. The normality and homoscedasticity assumptions have negligible effects again.

Table 8 Variance decomposition of the estimation error of the expected $\text {E}\rho ^2$, $\varPhi$ and F of a new collection

8 Discussion

In this paper we were able to study for the first time the true behavior of various estimators of test collection accuracy and reliability. Thanks to the proposed algorithm of stochastic simulation, we were able to simulate arbitrarily large collections where the expected mean system scores are fixed and known upfront. This allowed us to quantify the bias of the estimates and their robustness to several statistical assumptions. The results showed that the common estimators used in the literature are biased. In the particular case of the Kendall $\tau$ and $\tau _{AP}$ correlations, as well as of the measures from generalizability theory, the estimates tend to be negatively biased: they underestimate the similarity between the results of a test collection and the true system scores. This is an important result that requires further examination, as a number of studies recently suggested that test collections are generally much smaller than they should, such as Sakai (2014b), Urbano et al. (2013b) and Webber et al. (2008).

The results evidence the problems of split-half methods to estimate collection accuracy. First, the model they internally fit to the observations is usually selected based on its goodness of fit to sets of up to $n_t/2$ topics, and not on the grounds of theoretical arguments. For instance, the three models in Fig. 2 seem to provide similarly good fits of the data in the right plot, but the extrapolations diverge quite significantly as the number of topics increases. There is in principle no theoretical basis for choosing one or another, but clearly one of them should be better than the others. One could even say that, visually, the exp1 and logit models (red and blue) seem to give a better fit, but the results in Sects. 6 and 7 actually show that it is exp2 (green) the one that is less biased. At the very least, the results confirm that there is no single model suitable to all measures, and we even find that some models perform well for estimating the accuracy of an existing collection, but not to estimate the expected accuracy of a larger collection.

The second problem, already identified for instance by Sanderson and Zobel (2005), is that the split-half observations are not independent. In any given trial, the selection of topics for the second split is restricted by the random selection of topics for the first split, because there is a limited number of existing data. The consequence is that even if the model to fit is correct, it will be fitted to biased observations. This distinction is directly accounted for and modeled in statistical theory when defining measures like $\text {E}\rho ^2$. As we mentioned earlier, it corresponds to the expected square of the correlation between the observed scores and the true scores, but it also corresponds to the expected value of the correlation (not squared) between the observed scores in pairs of randomly parallel collections of the same size (Cronbach et al. 1972). The former is the quantity we are really interested in, and the latter is what split-half estimators actually provide (Allen and Yen 1979). We can directly observe this behavior in the estimates of $\tau$ in Fig. 9. The $\text {E}\tau$ and $\text {E}\tau _{AP}$ estimates converge to the actual expected accuracy $\varvec{E}_{n_t'}A(\vec{X}',\mathbf {\mu })$, but the split-half estimates converge to our estimates $\varvec{E}_{n_t'}\hat{A}(\vec{X}',\mathbf {\mu })$ of accuracy. Because the extrapolation models are rather arbitrary, and the observations used to fit them are not really independent, their estimates are the expected (biased) estimate of accuracy and not the expected (true) accuracy. Since $\text {E}\tau$ and $\text {E}\tau _{AP}$ are unbiased, they do estimate the expected true accuracy.

In terms of statistical assumptions, we have seen that the normality assumption has negligible effect. This can be explained by the fact that even when the raw effectiveness distributions diverge largely from normality, the residual distributions are approximately normal, as in Fig. 1. In addition, we note that effectiveness measures are often defined as the sum of some form of utility across the ranking of documents, suggesting that the Central Limit Theorem may actually be at play with sufficiently large evaluation cut-offs. The homoscedasticity assumption had a negligible effect as well. However, we must note that the simulation algorithm is designed to reproduce the actual residual distributions observed in the original collection, and not some other distributions that maximize the level of heteroscedasticity. That is, the simulated collections are heteroscedastic to the same extend that the original collection is so. In practice, the level of heteroscedasticity is not necessarily large, so this assumption did not affect estimates significantly. The levels of divergence from normality and heteroscedasticity are in principle easy to control in the simulation algorithm, allowing us to simulate some sort of adversarial systems from the point of view of evaluation. Additionally, we can study better ways of preserving the dependence structure of the original data. In the algorithm proposed here we focused on preserving the correlation matrix, but other aspects may be of interest, especially given that scores are bounded between 0 and 1. These are lines of work we intend to pursue.

We also note that there are several other sources of variability taking place in IR evaluation. In this paper we only studied the variability due to topics, but several works have shown that variability due to relevance assessors (Voorhees et al. 1998; Carterette and Soboroff 2010; Bailey et al. 2008), document corpus (Robertson and Kanoulas 2012; Sanderson et al. 2012), effectiveness measures and pool depth (Buckley and Voorhees 2000; Voorhees et al. 2001; Kekäläinen 2005; Sakai 2006; Buckley et al. 2007), and even users (Carterette et al. 2011), are not negligible. It is certainly worthwhile to extend the simulation algorithm to incorporate all these factors as well. Also, we note that there are other measures besides the ones we study here, such as the $d_{rank}$ distance (Carterette 2009) or variations of the rank correlations (Melucci 2007). Similarly, in this paper we focused on the F test because we were interested in simultaneously comparing a set of systems, but there are other statistical tests that can be used to compare individual pairs of systems, such as the t test, Wilcoxon, bootstrap or permutation tests (Hull 1993; Sakai 2006; Smucker et al. 2007; Urbano et al. 2013a), which can be further coupled with methods to adjust p-values for multiple comparisons (Carterette 2012; Boytsov et al. 2013). We leave these lines for further work as well, especially the study, via simulation, of the actual Type I and Type II error rates of various statistical significance tests.

We note that $\text {E}\tau$ and $\text {E}\tau _{AP}$ are unbiased provided that the $W_{ij}$ estimates in Eq. (35) are unbiased too. However, it is hard to ensure unbiasedness for arbitrary measures producing arbitrary distributions. The Central Limit Theorem applies, but it requires a couple dozen topics to work well. In particular, Figs. 6 and 9 show that the estimates from small available data are biased, probably because of the difficulty in estimating the population standard deviation from a small sample. Even though the estimators behave very well with more than 20 topics, we should study how to compute better estimates of $W_{ij}$. The estimators can also be extended to incorporate thresholds below which two systems are considered equal, therefore accounting for ties.

Finally, throughout this paper we have worked exclusively with point estimates, but we should fully consider interval estimates as well. The split-half estimators can produce intervals from the model they fit internally, confidence intervals have been derived for the measures from generalizability theory, and simple intervals can be computed for the proposed $\text {E}\tau$ and $\text {E}\tau _{AP}$ estimators. Even though most of the point estimates are shown to be biased, this bias can probably be corrected in practice if we use intervals. We leave this line for future work as well.

9 Conclusions

In this paper we discussed the measurement of test collection reliability from the perspective of traditional ad hoc measures and statistical measures as well. Past research on this topic was partially limited because we do not know the true mean effectiveness of systems, so it is impossible to assess how accurate our measurements really are. The best approximation involves split-half methods, but this approach is unfortunately limited by the lack of a theoretical basis, and the available data. To overcome this limitation in IR evaluation research, we proposed an algorithm for stochastic simulation of evaluation results. The algorithm simulates arbitrarily large test collections for the set of systems and universe of topics represented by some previously available test collection, allowing us to fix the true system scores upfront and to control what statistical assumptions hold. Through several indicators, we diagnosed how realistic the simulations are and how close they resemble real TREC evaluation data. The results showed that the simulated collections are indeed realistic, opening new opportunities for IR evaluation research where it is necessary to know the true effectiveness of systems.

Through large-scale simulation from TREC data, we evaluated the bias of estimators in a first scenario where we are interested in the accuracy of an existing test collection. The results showed that ad hoc measures tend to underestimate the actual reliability of collections, especially when the number of topics is rather small. As a consequence, they suggest the use of more topics than actually needed. On the other hand, the statistical measures from generalizability theory provide much better estimates, even though for very small collections they tend to underestimate reliability as well. Finally, we saw that the proper definition of target effect sizes is a non-trivial problem when estimating the power of the F test.

We also evaluated the bias of the measures in a second scenario where we want to estimate the expected accuracy of a new test collection of arbitrary size based on the data available from previous collections. The results confirm that the estimates depend largely on the amount of data previously available. For instance, the $\tau$ and $\tau _{AP}$ correlations of hypothetical large collections are very underestimated unless we have about 100 topics already. In fact, there is a very clear correlation between the number of topics available from the previous collection, and the bias of the estimates, indicating that predictions of the required number of topics to include in a collection under development are highly overestimated. For the generalizability theory measures we found much smaller biases, especially for small numbers of topics. In general, with initial collections of about 50 topics we get quite accurate estimates. To overcome the limitations of the split-half extrapolation of $\tau$ and $\tau _{AP}$, we proposed two new estimators, called $\text {E}\tau$ and $\text {E}\tau _{AP}$, based on statistical principles. The results confirm that they are unbiased and consistent estimators, behaving much better than the split-half alternatives and at a smaller computational expense.

Finally, we studied how robust these measures are to violations of statistical assumptions. In general, we found that all measures are robust to the normality and homoscedasticity assumptions, because the actual distributions do not depart much from these assumptions in practice. We found a slight effect of the uncorrelated effects assumption, especially on the ad hoc measures in the first scenario and the statistical measures in the second scenario. In terms of random sampling, we found generally small effects except with the statistical measures. Even though the effects are smaller than in principle thought, when absolute scores are of interest we can have very high errors if random sampling is not guaranteed. The split-half estimation of the ad hoc measures partially alleviates this problem because they actually involve a form of resampling. In both scenarios, the most important factor is usually the amount of available data.

We created several scripts for the statistical software R to easily simulate new collections and help researchers analyze the reliability of test collection designs. They can be downloaded from http://github.com/julian-urbano/irj2015-reliability.