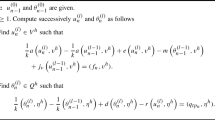The plane contact problem of the transfer of a horizontal load from a weakly inhomogeneous infinite stringer to a prestressed elastic strip clamped at one edge is solved using the linearized theory of elasticity. The solution has a general form for the theory of large initial deformations and different theories of small initial deformations for an arbitrary elastic potential. The problem for the normal and tangential contact stresses is reduced to a governing system of recurrent systems of integro-differential equations, which is solved in powers of a small parameter. The zero-order approximation of the inhomogeneous problem is derived using the Fourier transform. The contact stresses are represented by Fourier integrals.
Similar content being viewed by others
References
A. N. Guz, S. Yu. Babich, and Yu. P. Glukhov, Mixed Problems for a Prestressed Elastic Foundation [in Russian], Lambert Academic Publishing, Saarbrücken (2015).
O. M. Guz, S. Yu. Babich, and V. B. Rudnitskii, Contact Interaction of Prestressed Bodies [in Ukrainian], Vyshcha Shkola, Kyiv (1995).
M. M. Dikhtyaruk, “Determining the influence function for an elastic strip with initial (residual) stresses," in: Proc. 4th Int. Symp. on Tribo-Fatigue (September 23–27, 2002, Ternopil) [in Ukrainian], Ternop. Derzh. Tekhn. Univ. im. Ivana Pulyuya, Ternopil (2002), pp. 426–431.
M. M. Dikhtiaruk, “Periodic contact problem for an elastic band with initial (residual) stresses,” Dop. NAN Ukrainy, No. 3, 46–49 (2004).
V. S. Sarkisyan, Contact Problems for Half-Planes and Strips with Elastic Pads [in Russian], Izd. Yerevan. Univ., Yerevan (1983).
I V. N. Akopyan, S. A. Mirzoyan, and S. M. Mkhitaryan, “The problem of the contact between a broken stringer and an elastic infinite strip containing a vertical edge crack,” Int. Appl. Mech., 51, No. 2, 176–186 (2015).
V. M. Aleksandrov, “Optimal control of linear systems with interval constraints,” Zh. Vychisl. Mat. Mat. Fiz., 55, No. 5, 758–775 (2015).
S. Yu. Babich, A. N. Guz, and V. B. Rudnitsky, “Contact problems for prestressed elastic bodies and rigid and elastic punches,” Int. Appl. Mech., 40, No. 7, 744–765 (2004).
S. Yu. Babich, N. N. Dikhtyaruk, and S. V. Degtyar, “Contact problem for two identical strips reinforced by periodically arranged fasteners with initial,” Int. Appl. Mech., 55, No. 6, 629–635 (2019).
E. I. Bespalova, “Resonant electromechanical vibrations of piezoelectric plates,” Int. Appl. Mech., 50, No. 6, 651–663 (2014).
A. N. Guz, “Establishing the foundations of the mechanics of fracture of materials compressed along cracks (review),” Int. Appl. Mech., 50, No. 1, 1–57 (2014).
A. N. Guz, “Ultrasonic nondestructive method for stress analysis of structural members and near-surface layers of materials: focus on Ukrainian research (review),” Int. Appl. Mech., 50, No. 3, 231–252 (2014).
A. N. Guz, “Recognition of the achievements of the S. P. Timoshenko Institute of Mechanics by the world’s scientific community,” Int. Appl. Mech., 51, No. 1, 1–11 (2015).
A. N. Guz, “Nonclassical problems of fracture/failure mechanics: on the occasion of the 50th anniversary of the research (review) II,” Int. Appl. Mech., 55, No. 3, 239–295 (2019).
A. N. Guz and A. M. Bagno, “Influence of prestresses on quasi-lamb modes in hydroelastic waveguides,” Int. Appl. Mech., 56, No. 1, 1–12 (2020).
N. N. Dikhtyaruk, “Load transfer from the infinite stringer to the two jammed along one edge identical stripes with initial (residual) stresses,” Sci. J. Tern. Nat. Techn. Univ., 83, No. 3, 51–61 (2016).
N. N. Dikhtyaruk, “Equilibrium of a prestressed strip reinforced with elastic plates,” Int. Appl. Mech., 40, No. 3, 290–296 (2004).
N. N. Dikhtyaruk, O. V. Kurinenko, E. A. Poplavskaya, and N. N. Samaruk, “Interaction between a finite stringer and two identical prestressed strips: contact problem,” Int. Appl. Mech., 55, No. 1, 79–85 (2019).
P. Z. Lugovoi, V. F. Meish, Yu. A. Meish, and S. P. Orlenko, “Dynamic design of compound shell structures of revolution under nonstationary loads,” Int. Appl. Mech., 56, No. 1, 22–32 (2020).
O. P. Moses, A. O. Adewale, and O. A. Olusegun, “Numerical analysis of thermo-elastic contact problem of disc brakes for vehicle on gradient surfaces,” World J. Eng. Technol., 4, No. 1, 51–58 (2016).
V. B. Rudnitsky and N. N. Dikhtyaruk, “A prestressed elastic strip with elastic reinforcements,” Int. Appl. Mech., 38, No. 11, 1354–1360 (2002).
V. B. Rudnitskii and N. N. Dikhtyaruk, “Interaction between an infinite stringer and two identical prestressed strips: contact problem,” Int. Appl. Mech., 53, No. 2, 149–155 (2017).
N. A. Yaretskaya, “Three-dimensional contact problem for an elastic layer and a cylindrical punch with prestresses,” Int. Appl. Mech., 50, No. 4, 378–388 (2014).
N. A. Yaretskaya, “The impact of the initial (residual) stresses on the contact interaction of elastic cylindrical punch and an elastic layer,” Bulletin of NAS of Ukraine, No. 1, 57–62 (2014).
W. K. Yuan, J. M. Long, Y. Ding, and G. F. Wang, “Micro/nanocontact between a rigid ellipsoid and an elastic substrate with surface tension,” J. App. Mech., 84, No. 1, 011–012 (2017).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Prikladnaya Mekhanika, Vol. 56, No. 6, pp. 69–78, November–December 2020.
This study was sponsored by the budget program “Support for Priority Areas of Scientific Research” (KPKVK 6541230).
Rights and permissions
About this article
Cite this article
Babich, S.Y., Dikhtyaruk, N.N. Load Transfer from an Infinite Inhomogeneous Stringer to a Prestressed Elastic Strip Clamped at One Edge*. Int Appl Mech 56, 708–716 (2020). https://doi.org/10.1007/s10778-021-01047-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-021-01047-9