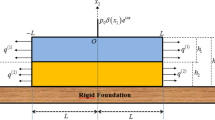
The dynamical stress field in a sandwich plate-strip is mathematically modeled using the piecewise-homogeneous body model and the three-dimensional linearized theory of electro-elastic waves in initially stressed bodies. The plate consists of a piezoelectric core perfectly bonded to elastic layers with initial stress, rests on a rigid foundation, and is subject to harmonic force. It is assumed that the piezoelectric material is poled perpendicularly to the free surface of the body. The governing system of partial differential equations of motion is solved by the finite-element method. The numerical results are presented, illustrating the effect of certain relationships of the problem of the propagation of stresses and electric displacements at the interfaces between the elastic layers and the piezoelectric core and between the plate-strip and the rigid foundation. The effect of the initial stress parameter and a change in the thickness of the piezoelectric core on the frequency response of the plate-strip is studied.
Similar content being viewed by others
References
J. R. Vinson, Plate and Panel Structures of Isotropic, Composite and Piezoelectric Materials, Including Sandwich Construction, Springer, Dordrecht (2005).
A. K. Nayak, S. S. J. Moy, and R. A. Shenoi, “Free vibration analysis of composite sandwich plates based on Reddy’s higher-order theory,” Composites, Part B, 33, No. 7, 505–519 (2002).
A. Chakrabarti and A. H. Sheikh, “Buckling of laminated sandwich plates subjected to partial edge compression,” Int. J. Mech. Sci., 47, No. 3, 418–436 (2005).
L. Hazard and P. Bouillard, “Structural dynamics of viscoelastic sandwich plates by the partition of unity finite element method,” Comput. Meth. Appl. Mech., 196, 4101–4116 (2007).
M. K. Pandit, B. N. Singh, and A. H. Sheikh, “Buckling of laminated sandwich plates with soft core based on an improved higher order zigzag theory,” Thin. Wall. Struct., 46, No. 11, 1183–1191 (2008).
S. Xiang, K. Wang, Y. Ai, Y. Sha, and H. Shi, “Analysis of isotropic, sandwich and laminated plates by a meshless method and various shear deformation theories,” Compos. Struct., 91, No. 1, 31–37 (2009).
R. Li, G. A. Kardomateas, and G. J. Simitses, “Point-wise impulse (blast) response of a composite sandwich plate including core compressibility effects,” Int. J. Solids. Struct., 46, No. 10, 2216–2223 (2009).
T. M. Tu, L. N. Thach, and T. H. Quoc, “Finite element modeling for bending and vibration analysis of laminated and sandwich composite plates based on higher-order theory,” Comp. Mater. Sci., 49, No. 4, 390–394 (2010).
S. M. Hasheminejad and B. Gheshlaghi, “Three-dimensional elastodynamic solution for an arbitrary thick FGM rectangular plate resting on a two parameter viscoelastic foundation,” Compos. Struct., 94, No. 9, 2746–2755 (2012).
S. D. Akbarov and N. Yahnioglu, “Buckling delamination of a sandwich plate-strip with piezoelectric face and elastic core layers,” Appl. Math. Model., 37, 8029–8038 (2013).
M. A. R. Loja, C. M. M. Soares, and J. I. Barbosa, “Analysis of functionally graded sandwich plate structures with piezoelectric skins using B-spline finite strip method,” Compos. Struct., 96, 606–615 (2013).
M. Shahraeeni, R. Shakeri, and S. M. Hasheminejad, “An analytical solution for free and forced vibration of a piezoelectric laminated plate coupled with an acoustic enclosure,” Comput. Math. Appl., 69, No. 11, 1329–1341 (2015).
A. Sankar, S. Natarajan, and M. Ganapathi, “Dynamic instability analysis of sandwich plates with CNT reinforced facesheets,” Compos. Struct., 146, No. 20, 187–200 (2016).
A. N. Guz, Elastic Waves in a Body with Initial (Residual) Stresses, A.S.K., Kiev (2004).
J. Yang, An Introduction to the Theory of Piezoelectricity, Springer, New York (2005).
A. Dașdemir and M. Eröz, “Mathematical modeling of dynamical stress field problem for a pre-stressed bi-layered plate-strip,” Bull. Malays. Math. Sci. Soc., 38, No. 2, 733–760 (2015).
O. C. Zienkiewicz and R. L. Taylor, The Finite Element Method, Vol. 1. Basic Formulation and Linear Problems, McGraw-Hill, London (1989).
Y. S. Uflyand, Integral Transformations in the Theory of Elasticity, USSR Academy of Science, Moscow–Leningrad (1963).
Author information
Authors and Affiliations
Corresponding author
Additional information
Published in Prikladnaya Mekhanika, Vol. 54, No. 4, pp. 125–144, July–August, 2018.
* The author is a member of the research project supported by the Research Fund of Kastamonu University under project KÜ-BAP01/2015-3.
Rights and permissions
About this article
Cite this article
Dașdemir, A. Forced Vibrations of Pre-Stressed Sandwich Plate-Strip with Elastic Layers and Piezoelectric Core*. Int Appl Mech 54, 480–493 (2018). https://doi.org/10.1007/s10778-018-0901-3
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-018-0901-3