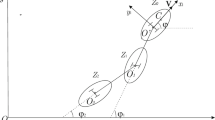
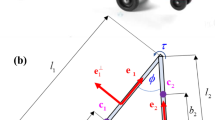
The kinematics of a two-link mobile robot with three steerable wheels moving in an L-shaped corridor is analyzed. A smooth (with continuous first derivative) path is designed maintaining the optimal maneuverability of the vehicle. The motion of the vehicle along this path is planned. Analytical expressions for the reactions at the contact of the wheels with the ground are given in the general case of motion. The radius of curvature of the programmed path is shown to have a strong influence on the reactions.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. B. Larin, “On path planning for a compound wheeled vehicle,” Int. Appl. Mech., 46, No. 3, 323–329 (2010).
V. B. Larin, “Determining the constraint forces for a two-link robotic vehicle with three steerable wheels,” Int. Appl. Mech., 46, No. 4, 450–454 (2010).
A. I. Lurie, Analytical Mechanics, Springer, Berlin–New York (2002).
F. J. Almeida, L. Pereira, and J. Borges-Sousa, “On the design of a hybrid feedback control system for a non-holonomic car-like vehicle,” in: Proc. 4th European Control Conf. (ECC97), Brussels, Belgium (1997), pp. 1–4.
I. I. Anik’ev, M. I. Mikhailova, and E. A. Sushchenko, “Experimental determination of the reaction of an elastic cantilever–rod system to a shock wave,” Int. Appl. Mech., 48, No. 6, 736–743 (2012).
E. Ya. Antonyuk and A. T. Zabuga, “Synthesis of a program trajectory for a wheeled vehicle to bypase side obstacles,” Int. Appl. Mech., 44, No. 9, 1065–1073 (2008).
A. M. Bloch, Nonholonomic Mechanics and Control, Springer-Verlag, New York (2003).
A. E. Bryson, Jr., and Ho-Yu-Chi, Applied Optimal Control. Optimization, Estimation and Control, Braisdell, Waltham, Massachusetts (1969).
A. E. Bryson, Jr., and Ho-Yu-Chi, Applied Optimal Control. Optimization, Estimation and Control, Braisdell, Waltham, Massachusetts (1969).
W. Goldsmith, Impact, London (1960).
J. A. Zukas, T. Nicholas, H. F. Swift, L. B. Greszczuk, and D. R. Curran, Impact Dynamics, New York (1982).
I. I. Hussein and A. M. Bloch, “Optimal control of underactuated nonholonomic mechanical systems,” IEEE Trans. Automat. Control, 53, No. 3, 668–682 (2008).
V. B. Larin, “The control of manipulators and wheeled transport robots as systems of rigid bodies,” Int. Appl. Mech., 36, No. 4, 449–481 (2000).
V. B. Larin, “Control of a compound wheeled vehicle with two steering wheels,” Int. Appl. Mech., 44, No. 12, 1413–1420 (2008).
A. A. Martynyuk and N. V. Nikitina, “Bifurcation processes in periodically perturbed systems,” Int. Appl. Mech., 49, No. 1, 114–123 (2013).
G. Oriolo, S. Panzleri, and G. Ulivi, “Cyclic learning control of chained-form systems with application to car-like robots,” in: Proc. IFAC 13th Trienni World Congr. on Mobile Robots, San Francisco (1996), pp. 187–192.
L. A. Pars, A Treatise on Analytical Dynamics, Heinemann, London (1964).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Prikladnaya Mekhanika, Vol. 50, No. 2, pp. 134–144, March–April 2014.
Rights and permissions
About this article
Cite this article
Antonyuk, E.Y., Zabuga, A.T. Dynamics of a Two-Link Vehicle in an L-Shaped Corridor Revisited. Int Appl Mech 50, 222–230 (2014). https://doi.org/10.1007/s10778-014-0626-x
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-014-0626-x