Abstract
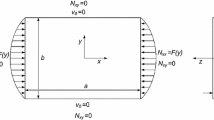
The paper outlines a method for studying the vibrations of plates of complex geometry subjected to in-plane loading. The method is based on the R-function and variational methods. It is used to plot frequency response of plates with complex geometry and different boundary conditions
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. V. Bolotin, Dynamic Stability of Elastic Systems [in Russian], Gostekhizdat, Moscow (1956).
A. S. Vol’mir, Nonlinear Dynamics of Plates and Shells [in Russian], Nauka, Moscow (1972).
É. I. Grigolyuk, Vibrations of a Shallow Cylindrical Panel Undergoing Finite Deflections [in Russian], Nauka, Moscow (1955).
Ya. M. Grigorenko and V. I. Gulyaev, “Nonlinear problems of shell theory and their solution methods (review),” Int. Appl. Mech., 27, No. 10, 929–947 (1991).
Ya. M. Grigorenko, V. I. Gulyaev, E. S. Dekhtyaryuk, and V. V. Chemolaev, “Stability of nonlinear vibrations of shallow rectangular (in plan) cylindrical shells,” Mekh. Tverd. Tela, No. 6, 137–142 (1983).
Ya. M. Grigorenko, Ya. G. Savula, and I. S. Mukha, “Linear and nonlinear problems on the elastic deformation of complex shells and methods of their numerical solution,” Int. Appl. Mech., 36, No. 8, 979–1000 (2000).
V. D. Kubenko, P. S. Koval’chuk, and T. S. Krasnopol’skaya, Nonlinear Interaction of Flexural Vibration Modes of Cylindrical Shells [in Russian], Naukova Dumka, Kyiv (1984).
V. D. Kubenko and P. S. Koval’chuk, “Nonlinear problems of the vibration of thin shells (review),” Int. Appl. Mech., 34, No. 8, 703–728 (1998).
V. L. Rvachev and L. V. Kurpa, R-Functions in Problems of the Theory of Plates [in Russian], Naukova Dumka, Kyiv (1987).
J. Awrejcewicz and A. V. Krys’ko, “Analysis of complex parametric vibrations of plates and shells using Bubnov-Galerkin approach,” Appl. Mech., 73, 495–504 (2003).
A. Ya. Grigorenko, “Numerical analysis of stationary dynamic processes in anisotropic inhomogeneous cylinders,” Int. Appl. Mech., 41, No. 8, 831–866 (2005).
A. Ya. Grigorenko and T. L. Efimova, “Spline-approximation method applied to solve natural-vibration problems for rectangular plates of varying thickness,” Int. Appl. Mech., 41, No. 10, 1160–1169 (2005).
P. S. Koval’chuk, “Nonlinear vibrations of a cylindrical shell containing a flowing fluid,” Int. Appl. Mech., 41, No. 4, 405–412 (2005).
L. V. Kurpa and A. B. Linnik, “Studying the vibrations of in-plane loaded plates of variable thickness,” Int. Appl. Mech., 41, No. 1, 62–69 (2005).
F. Moussaoi and R. Benamar, “Non-linear vibrations of shell-type structures review with bibliography,” J. Sound Vibr., 225, No. 1, 345–355 (2002).
Author information
Authors and Affiliations
Additional information
__________
Translated from Prikladnaya Mekhanika, Vol. 42, No. 12, pp. 124–132, December, 2006.
Rights and permissions
About this article
Cite this article
Kurpa, L.V., Masur, O.S. Studying the nonlinear vibrations of statically compressed plates. Int Appl Mech 42, 1421–1429 (2006). https://doi.org/10.1007/s10778-006-0212-y
Received:
Issue Date:
DOI: https://doi.org/10.1007/s10778-006-0212-y