Dynamic State Reconstruction of Quantum Systems Subject to Pure Decoherence

Abstract

The article introduces efficient quantum state tomography schemes for qutrits and entangled qubits subject to pure decoherence. We implement the dynamic state reconstruction method for open systems sent through phase-damping channels, which was proposed in: Czerwinski and Jamiolkowski Open Syst. Inf. Dyn. 23, 1650019 (2016). In the present article we prove that two distinct observables measured at four different time instants suffice to reconstruct the initial density matrix of a qutrit with evolution given by a phase-damping channel. Furthermore, we generalize the approach in order to determine criteria for quantum tomography of entangled qubits. Finally, we prove two universal theorems concerning the number of observables required for quantum state tomography of qudits subject to pure decoherence. We believe that dynamic state reconstruction schemes bring advancement and novelty to quantum tomography since they utilize the Heisenberg representation and allow to define the measurements in time domain.

1 Introduction

Quantum state tomography, i.e. the problem of reconstructing the accurate representation of a physical system from measurements, is crucial for quantum information and computation. It has been an important line of research since 1933, when Wolfgang Pauli asked whether a wave function can be determined from the position and momentum distributions. For years, much has been written about quantum tomography (e.g. [1,2,3,4,5,6]), but still many fundamental questions remain to be answered.

The ability to recover quantum states from measurements is particularly relevant to quantum communication which requires well-characterized quantum resources to encode information. Quantum tomography frameworks are commonly used in order to evaluate the effectiveness of information processing in the case of an imperfect measurements scenario, e.g. [7,8,9].

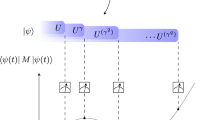
Among many different methods of quantum tomography, special attention should be paid to the so-called stroboscopic approach, which was originally introduced in 1983 by Andrzej Jamiolkowski [10]. This approach aims to reconstruct the initial density matrix by the lowest possible number of distinct observables due to the utilization of the knowledge about the evolution of a quantum system (encoded, for example, in a GKSL equation [11, 12]). For a given linear generator of evolution, one can compute the index of cyclicity, which expresses the minimal number of distinct observables required for quantum tomography [13,14,15]. The mean value of each observable is measured at several time instants over different copies of the system (prepared in the same unknown initial state).

The search for the minimal number of distinct observables which provide complete information about an unknown quantum system is in line with the classic work on density matrices characterized by the mean values of Hermitian operators [16], as well as with other results concerning the quorum of observables [17, 18]. The stroboscopic approach to quantum tomography appears to have a great potential for experimental applications since it allows to obtain an unknown density matrix by devising few measurement setups.

In [19] the stroboscopic approach has been reformulated and applied to quantum systems which are sent through phase-damping channels (pure decoherence). This kind of quantum dynamics stems from fundamental results of the theory of open systems, and properties of such channels have been widely studied, e.g. [20]. Therefore, it seems utterly justified to analyze this time-evolution model in the context of dynamic quantum tomography. In [19] the quantum tomography problem was solved for two specific phase-damping channels – qubits subject to dephasing and qudits with evolution given by Gaussian semigroups.

In Section 2, we revise the theoretical background concerning the dynamic quantum tomography model for systems subject to pure decoherence. Then, we introduce novel results which are included in the three subsequent sections. First, we prove that one can reconstruct the initial state of a qutrit on the basis of the mean values of 2 observables measured at 4 distinct time instants. Next, we analyze the optimal criteria for the quantum tomography of 4 −level quantum systems. Special attention is paid to entangled qubits as a classic example of such systems. Finally, we formulate general theorems concerning qudits subject to pure decoherence. We prove that two observables are sufficient to determine all off-diagonal elements of any density matrix. In addition, we give the upper bound for the number of distinct observables required for the quantum state tomography of N −level open systems subject to pure decoherence.

Throughout the article, we shall use the following notations. Let ${\mathscr{H}}$ stand for a finite dimensional Hilbert space ($\dim {\mathscr{H}} = N < \infty$) associated with a physical system. Then, by $\mathcal {S}({\mathscr{H}})$ we shall denote the state set, i.e. the set of all legitimate density operators: $\mathcal {S}({\mathscr{H}}) = \{\rho : {\mathscr{H}} \rightarrow {\mathscr{H}}, \rho \geq 0, \text { Tr } \rho = 1\}$. Furthermore, we shall use ${\mathscr{B}}({\mathscr{H}})$ in reference to the space of all linear operators on ${\mathscr{H}}$ and ${\mathscr{B}}_{*} \mathcal {(H)}$ to denote the space of all Hermitian (self-adjoint) operators on ${\mathscr{H}}$. Finally, $\mathbb {M}_{N} (\mathbb {C})$ shall denote the vector space of N × N complex matrices.

2 Quantum Tomography for Phase-Damping Channels – Revision

In this section, we shall briefly revise the dynamic approach to quantum tomography of open systems subject to pure decoherence introduced in [19]. Henceforth, we adopt the standard basis in ${\mathscr{H}}$. Since the basis is fixed, every density operator $\rho \in \mathcal {S}({\mathscr{H}})$ has its matrix representation. First, let us recall the definition of a phase-damping channel, assuming that ρ(0) denotes the initial density matrix.

Definition 1

A one-parameter family of maps {Φ_t,t ≥ 0}, acting ${\varPhi }_{t}: {\mathscr{B}}({\mathscr{H}}) \rightarrow {\mathscr{B}}({\mathscr{H}})$, of the following form:

$$ {\varPhi}_{t} [\rho(0)] = D(t) \circ \rho(0) \equiv \rho(t), $$

(1)

where ∘ denotes the Hadamard product and $D(t) \in \mathbb {M}_{N} (\mathbb {C})$ satisfies the conditions:

$$ \begin{array}{ll} &1. \forall t \geq 0 D(t) \geq 0, \\ &2. \forall t \geq 0 d_{ii} (t) =1 \text{for} i=1,\dots, N,\\ &3. d_{ij}(0) =1 \text{for} i,j=1,\dots, N. \end{array} $$

(2)

defines a legitimate quantum dynamics which shall be called a phase-damping channel.

The conditions (2) enumerated in the definition guarantee that the map (1) is completely positive and trace-preserving (CPTP) for any t ≥ 0 and it satisfies the initial condition: Φ₀[ρ(0)] = ρ(0), which makes it a time-dependent quantum channel. In other words, it can be proved that the map (1) can be converted into the Kraus representation [21], which means that Φ_t for any t ≥ 0 can be considered a superoperator such that ${\varPhi }_{t}: \mathcal {S}({\mathscr{H}}) \rightarrow \mathcal {S}({\mathscr{H}})$. The matrix D(t) shall be referred to as the dynamic matrix.

The goal of quantum state tomography is to reconstruct the initial density matrix ρ(0) based on data accessible from an experiment. We assume that there is a set of observables $\{Q_{1}, \dots , Q_{r}\}$ and each of them can be measured at discrete time instants $\{t_{1}, \dots , t_{p}\}$. Thus, from an experiment we can obtain a matrix of data, denoted by [m_i(t_j)]. The elements of this matrix can be expressed as:

$$ m_{i} (t_{j}) = \text{ Tr } \left\{ Q_{i} (D(t_{j}) \circ \rho(0))\right\}, $$

(3)

where $i=1,\dots , r$ and $j=1, \dots , p$.

In [19] it was demonstrated that any continuous time-dependent matrix $D(t) \in \mathbb {M}_{N} (\mathbb {C})$ can be decomposed in the basis of μ linearly independent matrices $A_{k} \in \mathbb {M}_{N} (\mathbb {C})$:

$$ D(t) = \sum\limits_{k=1}^{\mu} \alpha_{k} (t) A_{k}, $$

(4)

where {α_k(t)} denotes a set of linearly independent functions $\alpha _{k} (t): \mathbb {R} \rightarrow \mathbb {C}$.

By implementing the relation between the Hadamard product and the standard matrix product (c.f. [19, 22]), one can write a very useful formula for the measurement results:

$$ m_{i} (t_{j}) = \sum\limits_{k=1}^{\mu} \alpha_{k} (t_{j}) \text{ Tr }\left\{ (Q_{i} \circ {A_{k}^{T}}) \rho(0) \right\}, $$

(5)

which, from the physical point of view, is equivalent to the switch from the Schrödinger picture to the Heisenberg representation.

One can notice that if the measurement of any observable Q_i is performed at distinct time instants $t_{1},\dots , t_{p}$, we obtain a set of p equations:

$$ \begin{array}{ll} & m_{i} (t_{1}) = \sum\limits_{k=1}^{\mu} \alpha_{k} (t_{1}) \text{ Tr }\left\{ (Q_{i} \circ {A_{k}^{T}}) \rho(0) \right\}, \\ &m_{i} (t_{2}) = \sum\limits_{k=1}^{\mu} \alpha_{k} (t_{2}) \text{ Tr }\left\{ (Q_{i} \circ {A_{k}^{T}}) \rho(0) \right\}, \\ & {\vdots} \\ & m_{i} (t_{p}) = \sum\limits_{k=1}^{\mu} \alpha_{k} (t_{p}) \text{ Tr }\left\{ (Q_{i} \circ {A_{k}^{T}}) \rho(0) \right\}. \end{array} $$

(6)

On the left-hand side of the system (6), one has a vector of data which is obtainable from an experiment, whereas on the right-hand side there is a matrix [α_k(t_j)] which is computable based on the algebraic structure of D(t). Thus, one can agree that the figures $\text { Tr }\left \{ (Q_{i} \circ {A_{k}^{T}}) \rho (0) \right \}$ (where $k=1,\dots ,\mu$) are computable from (6) if and only if rank[α_k(t_j)] = μ. This condition claims that the matrix [α_k(t_j)] has to have full rank, which, in practice, means that the number of measurements equals μ and [α_k(t_j)] is a square matrix.

Due to repeated measurements of the same observable (over distinct copies of the system), we compute the projections of ρ(0) onto a set of operators: $\{Q_{i} \circ {A_{1}^{T}}, \dots , Q_{i} \circ A_{\mu }^{T} \}$. The measurement procedure is then performed for each observable from the set $\{Q_{1}, \dots , Q_{r}\}$.

In order to be able to reconstruct the initial density matrix ρ(0) from the projections $\text { Tr }\left \{ (Q_{i} \circ {A_{k}^{T}}) \rho (0) \right \}$, the matrices from the set $\{Q_{i} \circ {A_{k}^{T}}\}$ where $i=1,\dots ,r$ and $k=1,\dots ,\mu$ have to span ${\mathscr{B}}_{*} ({\mathscr{H}})$, i.e. the space to which ρ(0) belongs. In other words, the set $\{Q_{i} \circ {A_{k}^{T}}\}$ where $i=1,\dots ,r$ and $k=1,\dots ,\mu$ has to be informationally complete.

3 Dynamic Quantum Tomography Model for Qutrits Subject to Pure Decoherence

3.1 Preliminaries

In the case of qutrits (i.e. $\dim {\mathscr{H}} =3$), in order to find a basis for the set of density matrices one can refer to the Gell-Mann matrices. We shall follow the notation from [23] and use $\{\lambda _{1},\lambda _{2}, \dots , \lambda _{8}\}$ to denote the matrices:

$$ \lambda_{1} = \left [ \begin{array}{lll} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 &0 \end{array} \right], \lambda_{2} = \left [ \begin{array}{lll} 0 & -i & 0 \\ i & 0 & 0 \\ 0 & 0 &0 \end{array} \right], \lambda_{3} = \left [ \begin{array}{lll} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 &0 \end{array} \right], \lambda_{4} = \left [ \begin{array}{lll} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 &0 \end{array} \right], $$

$$ \lambda_{5} = \left [ \begin{array}{lll} 0 & 0 & -i \\ 0 & 0 & 0 \\ i & 0 &0 \end{array} \right], \lambda_{6} = \left [ \begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 &0 \end{array} \right], \lambda_{7} = \left [ \begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & -i \\ 0 & i &0 \end{array} \right], \lambda_{8} = \frac{1}{\sqrt{3}}\left [ \begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -2 \end{array} \right]. $$

The Gell-Mann matrices are a generalization of the Pauli matrices and they span the Lie algebra of the SU(3) group. Thus, they satisfy the conditions:

$$ \lambda_{i} = \lambda_{i}^{*}, \text{ Tr } \lambda_{i} =0 \text{ and } \text{ Tr } \lambda_{i} \lambda_{j} = 2 \delta_{\ij}. $$

(7)

For a 3 −level quantum system, the unknown density matrix $\rho (0) \in \mathcal {S}({\mathscr{H}})$ can be decomposed in the basis of the generators of SU(3) [24]:

$$ \rho(0) = \frac{1}{3} \mathbb{I}_{3} + \frac{1}{2} \sum\limits_{i=1}^{8} \langle \lambda_{i} \rangle \lambda_{i}, $$

(8)

where 〈λ_i〉 is the expectation value of the observable λ_i and can mathematically be represented as 〈λ_i〉 = Tr {λ_iρ(0)}.

If one would like to solve the quantum tomography problem for a qutrit without taking advantage of the knowledge about evolution, it would be necessary to measure the mean values of 8 distinct observables: $\{\lambda _{1},\lambda _{2}, \dots , \lambda _{8}\}$ and then use the results to complete the formula for ρ(0) as in (8). Such a static approach to quantum state reconstruction appears impractical since in a laboratory it would be impossible to define 8 distinct physical quantities.

3.2 Evolution Model for Qutrits

Let us consider a 3 −level quantum system such that its trajectory is given by a time-dependent channel:

$$ \rho(t) = \left[ \begin{array}{lll} 1 & e^{-\gamma_{1} t} & e^{-\gamma_{2} t} \\ e^{-\gamma_{1} t} & 1 & e^{-\gamma_{3} t} \\ e^{-\gamma_{2} t} & e^{-\gamma_{3} t} & 1 \end{array} \right] \circ \rho(0), $$

(9)

where γ₁,γ₂,γ₃ are positive decoherence rates and ρ(0) denotes the unknown initial density matrix of a 3 −level system ($\rho (0) \in \mathcal {S}({\mathscr{H}})$). We additionally assume that γ_i≠γ_j for i≠j.

One can quickly check that the dynamic matrix D(t) from (9) satisfies the conditions (2). Therefore, the time-dependent channel from (9) describes a legitimate evolution, i.e. $\rho (t) \in \mathcal {S}({\mathscr{H}})$ holds for all t ≥ 0. The quantum channel defined in (9) belongs to the family of phase-damping channels, which means that we can implement the method from [19] in order to reconstruct the initial density matrix.

3.3 Results and Analysis

The main goal of this subsection is to prove that by taking advantage of the knowledge about the evolution (which is given by (9)) one can significantly decrease the number of distinct observables required for the ability to reconstruct the initial density matrix ρ(0).

We can formulate and prove the following theorem.

Theorem 1

The initial density matrix of a qutrit with evolution given by a phase-damping channel of the form (9) can be uniquely determined on the basis of the mean values of two Hermitian operators:

$$ Q_{1} = \left [ \begin{array}{lll} 1 & 1 & -i \\ 1 & -1 & -i \\ i & i &0 \end{array} \right] \text{ and } Q_{2} = \left [ \begin{array}{lll} \frac{1}{\sqrt{3}} & -i & 1 \\ i & \frac{1}{\sqrt{3}} & 1 \\ 1 & 1 & -\frac{2}{\sqrt{3}} \end{array} \right], $$

(10)

which are measured at four distinct time instants t₁,t₂,t₃,t₄ (without loss of generality, we can assume that: t₁ < t₂ < t₃ < t₄).

Proof

First, one has to notice that the dynamic matrix D(t) from (9) can be decomposed in the form:

$$ D(t) = \mathbb{I}_{3} + e^{-\gamma_{1} t} A_{1} + e^{-\gamma_{2} t} A_{2} + e^{-\gamma_{3} t} A_{3}, $$

(11)

where

$$ A_{1} = \left [ \begin{array}{lll} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right] A_{2} = \left [ \begin{array}{lll} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{array} \right] \text{ and } A_{3} = \left [ \begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array} \right]. $$

(12)

Applying (5) into this example, one gets a formula for the mean values of the observables:

$$ \begin{array}{@{}rcl@{}} m_{i} (t_{j}) &=& \text{ Tr }\{ (Q_{i} \circ \mathbb{I}_{3}) \rho(0)\} + e^{-\gamma_{1} t_{j}} \text{ Tr }\{ (Q_{i} \circ A_{1}) \rho(0)\}\\ &&+ e^{-\gamma_{2} t_{j}} \text{ Tr }\{ (Q_{i} \circ A_{2}) \rho(0)\}+ e^{-\gamma_{3} t_{j}} \text{ Tr }\{ (Q_{i} \circ A_{3}) \rho(0)\}. \end{array} $$

(13)

In the case of the observable Q₁, one can easily calculate that:

$$ Q_{1} \circ \mathbb{I}_{3} = \lambda_{3}, Q_{1} \circ A_{1} = \lambda_{1}, Q_{1} \circ A_{2} = \lambda_{5}, Q_{1} \circ A_{3} = \lambda_{7}, $$

(14)

where λ_i are the Gell-Mann matrices. This leads to the following formula for the measurement result:

$$ m_{i} (t_{j}) = \text{ Tr }\{ \lambda_{3} \rho(0)\} + e^{-\gamma_{1} t_{j}} \text{ Tr }\{ \lambda_{1} \rho(0)\} + e^{-\gamma_{2} t_{j}} \text{ Tr }\{ \lambda_{5} \rho(0)\} + e^{-\gamma_{3} t_{j}} \text{ Tr }\{ \lambda_{7} \rho(0)\}. $$

(15)

Assuming that the mean value of the observable Q₁ can be obtained at 4 distinct time instants t₁,t₂,t₃,t₄, one gets a matrix equation (compare with (6)):

$$ \left[ \begin{array}{c} m_{1} (t_{1}) \\ m_{1} (t_{2}) \\ m_{1} (t_{3}) \\ m_{1} (t_{4}) \end{array} \right] = \left[\begin{array}{cccc} 1 & e^{-\gamma_{1} t_{1}} & e^{-\gamma_{2} t_{1}} & e^{-\gamma_{3} t_{1}} \\ 1 & e^{-\gamma_{1} t_{2}} & e^{-\gamma_{2} t_{2}} & e^{-\gamma_{3} t_{2}} \\ 1 & e^{-\gamma_{1} t_{3}} & e^{-\gamma_{2} t_{3}} & e^{-\gamma_{3} t_{3}} \\ 1 & e^{-\gamma_{1} t_{4}} & e^{-\gamma_{2} t_{4}} & e^{-\gamma_{3} t_{4}} \end{array} \right] \left[ \begin{array}{c} \text{ Tr }\{ \lambda_{3} \rho(0)\} \\ \text{ Tr }\{ \lambda_{1} \rho(0)\} \\ \text{ Tr }\{ \lambda_{5} \rho(0)\} \\ \text{ Tr }\{ \lambda_{7} \rho(0)\} \end{array} \right]. $$

(16)

In the case of the observable Q₂, one can quickly calculate that:

$$ Q_{2} \circ \mathbb{I}_{3} = \lambda_{8}, Q_{2} \circ A_{1} = \lambda_{2}, Q_{2} \circ A_{2} = \lambda_{4}, Q_{2} \circ A_{3} = \lambda_{6}, $$

(17)

which yields the following formula for the mean value of Q₂ measured at the moment t_j:

$$ m_{i} (t_{j}) = \text{ Tr }\{ \lambda_{8} \rho(0)\} + e^{-\gamma_{1} t_{j}} \text{ Tr }\{ \lambda_{2} \rho(0)\} +e^{-\gamma_{2} t_{j}} \text{ Tr }\{ \lambda_{4} \rho(0)\} + e^{-\gamma_{3} t_{j}} \text{ Tr }\{ \lambda_{6} \rho(0)\}. $$

(18)

Analogously like before, let us assume that the mean value of the observable Q₂ can be obtained at 4 distinct time instants t₁,t₂,t₃,t₄. Then, one gets a matrix equation (compare with (6)):

$$ \left[ \begin{array}{c} m_{2} (t_{1}) \\ m_{2} (t_{2}) \\ m_{2} (t_{3}) \\ m_{2} (t_{4}) \end{array} \right] = \left[\begin{array}{cccc} 1 & e^{-\gamma_{1} t_{1}} & e^{-\gamma_{2} t_{1}} & e^{-\gamma_{3} t_{1}} \\ 1 & e^{-\gamma_{1} t_{2}} & e^{-\gamma_{2} t_{2}} & e^{-\gamma_{3} t_{2}} \\ 1 & e^{-\gamma_{1} t_{3}} & e^{-\gamma_{2} t_{3}} & e^{-\gamma_{3} t_{3}} \\ 1 & e^{-\gamma_{1} t_{4}} & e^{-\gamma_{2} t_{4}} & e^{-\gamma_{3} t_{4}} \end{array} \right] \left[ \begin{array}{c} \text{ Tr }\{ \lambda_{8} \rho(0)\} \\ \text{ Tr }\{ \lambda_{2} \rho(0)\} \\ \text{ Tr }\{ \lambda_{4} \rho(0)\} \\ \text{ Tr }\{ \lambda_{6} \rho(0)\} \end{array} \right]. $$

(19)

One can observe that the matrix equations (16) and (19) are uniquely solvable if and only if:

$$ \det \left[\begin{array}{cccc} 1 & e^{-\gamma_{1} t_{1}} & e^{-\gamma_{2} t_{1}} & e^{-\gamma_{3} t_{1}} \\ 1 & e^{-\gamma_{1} t_{2}} & e^{-\gamma_{2} t_{2}} & e^{-\gamma_{3} t_{2}} \\ 1 & e^{-\gamma_{1} t_{3}} & e^{-\gamma_{2} t_{3}} & e^{-\gamma_{3} t_{3}} \\ 1 & e^{-\gamma_{1} t_{4}} & e^{-\gamma_{2} t_{4}} & e^{-\gamma_{3} t_{4}} \end{array} \right] \neq 0 $$

(20)

In order to demonstrate that this condition is satisfied, we can assume that the time instants t₁,t₂,t₃,t₄ are selected according to a certain rule. An assumption concerning the choice of time instants does not cause any loss in generality since one can agree that in an experiment it would be relatively easy to obey constraints imposed on the choice of moments of observation. If we assume that the time instants constitute an arithmetic sequence defined as: t₁ = t, t₂ = 2t, t₃ = 3t, t₄ = 4t, then the condition (20) can be rewritten as:

$$ \det \left[\begin{array}{cccc} 1 & \xi_{1} & \xi_{2} & \xi_{3} \\ 1 & (\xi_{1})^{2} & (\xi_{2})^{2} & (\xi_{3})^{2} \\ 1 & (\xi_{1})^{3} & (\xi_{2})^{3} & (\xi_{3})^{3} \\ 1 & (\xi_{1})^{4} & (\xi_{2})^{4} & (\xi_{3})^{4} \end{array} \right] \neq 0, $$

(21)

where $\xi _{i} = e^{-\gamma _{i} t}$. One can observe that the rows in the matrix are linearly independent as long as γ_i≠γ_j for i≠j, which means that the condition (21) is satisfied. Alternatively, one could notice that the matrix from (19) and (16) is an example of the generalized Vandermonde matrix, which means that it is always invertible under the settings of the Theorem 1 (cf. p. 99 in [25]). This implies that by solving both matrix equations (16) and (19), one can obtain the mean values Tr {λ_iρ(0)} where $i=1,\dots ,8$.

The solutions of (16) and (19) can be obtained on the basis of the mean values of the two selected observables Q₁ and Q₂. Thus, one can conclude that the figures Tr {λ_iρ(0)} for $i = 1,\dots , 8$ are computable from experimental data provided one knows the structure of the dynamic matrix D(t).

If the solutions of (16) and (19) are substituted to (8), one gets the explicit formula for the initial density matrix ρ(0), which means that the knowledge about the evolution of the system given by (9) combined with the measurements of the two observables Q₁ and Q₂ leads to the ability to reconstruct the unknown density matrix. This conclusion finishes the proof. □

One should note that Theorem 1 is existential and does not give a specific formula for the unknown density matrix. Due to the number of parameters, the analytical solution would have a long and unattractive form. Nevertheless, one can choose specific values of the decoherence parameters, as well as particular time instants, and then one is able to obtain a concrete formula for ρ(0) by following the general procedure introduced in this subsection.

4 Dynamic Quantum Tomography Model for Entangled Qubits Subject to Pure Decoherence

4.1 Preliminaries

Entangled qubits are a special case of quantum systems associated with the Hilbert space such that $\dim {\mathscr{H}} =4$. Thus, let us first analyze in general the quantum state tomography problem for 4 −level quantum systems subject to pure decoherence, and then apply the results to entangled qubits as a specific example of such systems.

In order to decompose any density matrix of a 4 −level quantum system, one can utilize the generalized Gell-Mann (GGM) basis (see Appendix), which consists of 15 elements [26]. There are 6 symmetric, 6 antisymmetric and 3 diagonal GGM matrices. One can expand any density matrix ρ(0) according to the formula (53).

In order to determine the initial density matrix of a 4 −level quantum system, one would have to measure the mean value of every GGM operator, which would deliver the Bloch vector. However, such an approach to quantum state tomography, although suggested in [24], does not seem practical. One is usually not able to define in a laboratory 15 distinct measurable quantities.

4.2 Evolution Model for 4 −Level Systems

Let us assume that the evolution of a 4 −level quantum system is given by a dynamical map of the form:

$$ \rho(t) = \left[ \begin{array}{cccc} 1 & e^{-\gamma_{1} t} & e^{-\gamma_{2} t} & e^{-\gamma_{3} t} \\ e^{-\gamma_{1} t} & 1 & e^{-\gamma_{4} t} &e^{-\gamma_{5} t} \\ e^{-\gamma_{2} t} & e^{-\gamma_{4} t} & 1 & e^{-\gamma_{6} t} \\ e^{-\gamma_{3} t} & e^{-\gamma_{5} t} & e^{-\gamma_{6} t} & 1 \end{array} \right] \circ \rho(0), $$

(22)

where $\gamma _{1}, \dots , \gamma _{6}$ are positive decoherence rates. We assume that γ_i≠γ_j for i≠j and $\rho (0)\in \mathcal {S}({\mathscr{H}})$ denotes the unknown initial density matrix.

One can confirm that the dynamic matrix D(t) from the definition (22) satisfies the conditions (2). Therefore, the channel defined in (22) describes a legitimate dynamical map. Thus, we shall apply the reasoning from [19] in order to investigate how one can benefit from the knowledge about the evolution when solving quantum state tomography problem.

4.3 Results and Analysis

The goal of this section is to demonstrate that the effectiveness of quantum state tomography can be significantly improved if we assume that the evolution of the quantum system is given by a phase-damping channel. We can formulate and prove a theorem.

Theorem 2

The initial density matrix ρ(0) of a 4 −level quantum system with evolution given by a phase-damping channel of the form (22) can be uniquely determined on the basis of the mean values of two observables:

$$ Q_{1} = \left [ \begin{array}{cccc} 1 & 1 & -i & 1 \\ 1 & -1 & -i & 1 \\ i & i & 0 & -i \\ 1 & 1 & i &0 \end{array} \right] \text{ and } Q_{2} = \left [ \begin{array}{cccc} \frac{1}{\sqrt{3}} & -i & 1 & -i \\ i & \frac{1}{\sqrt{3}} & 1 & -i \\ 1 & 1 & -\frac{2}{\sqrt{3}} & 1 \\ i & i & 1& 0 \end{array} \right], $$

(23)

which are measured at seven distinct time instants, and the mean value of the operator:

$$ {\varLambda}^{3} = \frac{1}{\sqrt{6}} \left [ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -3 \end{array} \right] $$

(24)

measured once at the time instant t = 0.

Proof

First, one has to notice that the dynamic matrix D(t) (from the channel definition (22)) can be decomposed in the form:

$$ D(t) = \mathbb{I}_{4} + e^{-\gamma_{1} t} A_{1} + e^{-\gamma_{2} t} A_{2} + e^{-\gamma_{3} t} A_{3} + e^{-\gamma_{4} t} A_{4} + e^{-\gamma_{5} t} A_{5} + e^{-\gamma_{6} t} A_{6}, $$

(25)

where

$$ \begin{array}{cc} & A_{1} = \left [ \begin{array}{cccc}{lll} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 &0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right] A_{2} = \left [ \begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right] A_{3} = \left [ \begin{array}{cccc} 0 & 0 & 0 &1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 &0 \end{array} \right]\\ & A_{4} = \left [ \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right] A_{5} = \left [ \begin{array}{cccc} 0 & 0 & 0 &0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 0 &0 \end{array} \right] A_{6} = \left [ \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right]. \end{array} $$

(26)

Applying this decomposition into (5), one gets a formula for the mean values of the observables:

$$ \begin{aligned} m_{i} (t_{j}) = {}&\text{ Tr }\{ (Q_{i} \circ \mathbb{I}_{4}) \rho(0)\} + e^{-\gamma_{1} t_{j}} \text{ Tr }\{ (Q_{i} \circ A_{1}) \rho(0)\}+ e^{-\gamma_{2} t_{j}} \text{ Tr }\{ (Q_{i} \circ A_{2}) \rho(0)\}\\& + e^{-\gamma_{3} t_{j}} \text{ Tr }\{ (Q_{i} \circ A_{3}) \rho(0)\}+ e^{-\gamma_{4} t_{j}} \text{ Tr }\{ (Q_{i} \circ A_{4}) \rho(0)\}+ \\& +e^{-\gamma_{5} t_{j}} \text{ Tr }\{ (Q_{i} \circ A_{5}) \rho(0)\}+ e^{-\gamma_{6} t_{j}} \text{ Tr }\{ (Q_{i} \circ A_{6}) \rho(0)\}. \end{aligned} $$

(27)

In the case of the observable Q₁, one can notice that:

$$ \begin{array}{ll} & Q_{1} \circ \mathbb{I}_{4} = {\varLambda}^{1}, Q_{1} \circ A_{1} = {\varLambda}_{s}^{12}, Q_{1} \circ A_{2} = {\varLambda}_{a}^{13}, Q_{1} \circ A_{3} = {\varLambda}_{s}^{14}\\ & Q_{1} \circ A_{4} = {\varLambda}_{a}^{23}, Q_{1} \circ A_{5} = {\varLambda}_{s}^{24}, Q_{1} \circ A_{6} = {\varLambda}_{a}^{34}, \end{array} $$

(28)

where ${\varLambda }_{s}^{jk}, {\varLambda }_{a}^{jk}, {\varLambda }^{l}$ are the GGM matrices. This leads to the following formula for the measurement result:

$$ \begin{array}{@{}rcl@{}} m_{i} (t_{j}) &=&\text{ Tr }\{ {\varLambda}^{1} \rho(0)\} + e^{-\gamma_{1} t_{j}} \text{ Tr }\{ {\varLambda}_{s}^{12} \rho(0)\} + e^{-\gamma_{2} t_{j}} \text{ Tr }\{ {\varLambda}_{a}^{13} \rho(0)\} + e^{-\gamma_{3} t_{j}} \text{ Tr }\{ {\varLambda}_{s}^{14} \rho(0)\} \\&&+e^{-\gamma_{4} t_{j}} \text{ Tr }\{ {\varLambda}_{a}^{23} \rho(0)\} + e^{-\gamma_{5} t_{j}} \text{ Tr }\{ {\varLambda}_{s}^{24} \rho(0)\}+ e^{-\gamma_{6} t_{j}} \text{ Tr }\{ {\varLambda}_{a}^{34} \rho(0)\}. \end{array} $$

(29)

Assuming that the mean value of the observable Q₁ can be obtained at 7 distinct time instants t₁,t₂,t₃,t₄,t₅,t₆,t₇, one gets a matrix equation (analogous to (19)):

$$ \left[ \begin{array}{c} m_{1} (t_{1}) \\ m_{1} (t_{2}) \\ {\vdots} \\ m_{1} (t_{7}) \end{array} \right] = \left[\begin{array}{cccc} 1 & e^{-\gamma_{1} t_{1}} & {\cdots} & e^{-\gamma_{6} t_{1}} \\ 1 & e^{-\gamma_{1} t_{2}} & {\cdots} & e^{-\gamma_{6} t_{2}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ 1 & e^{-\gamma_{1} t_{7}} & {\cdots} & e^{-\gamma_{6} t_{7}} \end{array} \right] \left[ \begin{array}{c} \text{ Tr }\{ {\varLambda}^{1} \rho(0)\} \\ \text{ Tr }\{ {\varLambda}_{s}^{12} \rho(0)\} \\ {\vdots} \\ \text{ Tr }\{ {\varLambda}_{a}^{34} \rho(0)\} \end{array} \right]. $$

(30)

On the other hand, for Q₂ one can quickly obtain:

$$ \begin{array}{ll} & Q_{2} \circ \mathbb{I}_{4} = {\varLambda}^{2}, Q_{2} \circ A_{1} = {\varLambda}_{a}^{12}, Q_{2} \circ A_{2} = {\varLambda}_{s}^{13}, Q_{2} \circ A_{3} = {\varLambda}_{a}^{14}\\ & Q_{2} \circ A_{4} = {\varLambda}_{s}^{23}, Q_{2} \circ A_{5} = {\varLambda}_{a}^{24}, Q_{2} \circ A_{6} = {\varLambda}_{s}^{34}, \end{array} $$

(31)

which gives us the following equation for the mean value of Q₂ at the moment t_j:

$$ \begin{array}{@{}rcl@{}} m_{i} (t_{j}) & =& \text{ Tr }\{ {\varLambda}^{2} \rho(0)\} + e^{-\gamma_{1} t_{j}} \text{ Tr }\{ {\varLambda}_{a}^{12} \rho(0)\} + e^{-\gamma_{2} t_{j}} \text{ Tr }\{ {\varLambda}_{s}^{13} \rho(0)\} + e^{-\gamma_{3} t_{j}} \text{ Tr }\{ {\varLambda}_{a}^{14} \rho(0)\} \\ && +e^{-\gamma_{4} t_{j}} \text{ Tr }\{ {\varLambda}_{s}^{23} \rho(0)\} + e^{-\gamma_{5} t_{j}} \text{ Tr }\{ {\varLambda}_{a}^{24} \rho(0)\}+ e^{-\gamma_{6} t_{j}} \text{ Tr }\{ {\varLambda}_{s}^{34} \rho(0)\}. \end{array} $$

(32)

We operate in the same vein as for the observable Q₁ and after 7 measurements at distinct time moments, we get a matrix equation:

$$ \left[ \begin{array}{c} m_{2} (t_{1}) \\ m_{2} (t_{2}) \\ {\vdots} \\ m_{2} (t_{7}) \end{array} \right] = \left[\begin{array}{cccc} 1 & e^{-\gamma_{1} t_{1}} & {\cdots} & e^{-\gamma_{6} t_{1}} \\ 1 & e^{-\gamma_{1} t_{2}} & {\cdots} & e^{-\gamma_{6} t_{2}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ 1 & e^{-\gamma_{1} t_{7}} & {\cdots} & e^{-\gamma_{6} t_{7}} \end{array} \right] \left[ \begin{array}{c} \text{ Tr }\{ {\varLambda}^{2} \rho(0)\} \\ \text{ Tr }\{ {\varLambda}_{a}^{12} \rho(0)\} \\ {\vdots} \\ \text{ Tr }\{ {\varLambda}_{s}^{34} \rho(0)\} \end{array} \right]. $$

(33)

One can observe that the matrix equations (30) and (33) are uniquely solvable if and only if:

$$ \det \left[\begin{array}{cccc} 1 & e^{-\gamma_{1} t_{1}} & {\cdots} & e^{-\gamma_{6} t_{1}} \\ 1 & e^{-\gamma_{1} t_{2}} & {\cdots} & e^{-\gamma_{6} t_{2}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ 1 & e^{-\gamma_{1} t_{7}} & {\cdots} & e^{-\gamma_{6} t_{7}} \end{array} \right] \neq 0 $$

(34)

In order to demonstrate that the condition (34) is satisfied, we follow the same strategy as in the case of qutrits. We assume that the time instants are not arbitrary and they constitute an arithmetic sequence defined as: t₁ = t, t₂ = 2t, $\dots$, t₇ = 7t. Then, the condition (34) can be rewritten as:

$$ \det \left[\begin{array}{cccc} 1 & \xi_{1} & {\cdots} & \xi_{6} \\ 1 & (\xi_{1})^{2} & {\cdots} & (\xi_{6})^{2} \\ {\vdots} & {\vdots} & {\ddots} & \vdots\\ 1 & (\xi_{1})^{7} & {\cdots} & (\xi_{6})^{7} \end{array} \right] \neq 0, $$

(35)

where $\xi _{i} = e^{-\gamma _{i} t}$ (for $i=1,\dots , 6$). One can observe that the rows in the matrix are linearly independent as long as the decoherence rates are positive and satisfy γ_i≠γ_j≠ 0 (for i≠j). This means that the condition (35) holds true. Consequently, by solving both matrix equations (30) and (33) one obtains the mean values of 14 operators which belong to the SU(4) generators. In general, a density matrix of a 4 −level quantum system is characterized by 15 parameters. Thus, one needs to perform the measurement of Λ³ at time instant t = 0 in order to get the complete set of information. When one knows the mean values of the GGM matrices, one is able to reconstruct the initial density matrix, which finishes the proof. □

4.4 Special Case: Entangled Qubits

In general, the density matrix of a 4 −level quantum system is fully determined by 15 real parameters. However, if one has a priori knowledge about the system in question, one can simplify the algebraic structure of the density matrix. In the case of $\dim {\mathscr{H}} =4$ one may consider entangled qubits as a specific example of quantum system.

Mixed-state entanglement can be defined by means of statistical mixture of the Bell states [27]. We shall introduce the following form of the initial quantum state of entangled qubits:

$$ \rho (0) = p_{1} |{{\varPhi}^{+}}\rangle\langle{{\varPhi}^{+}}| + p_{2} |{{\varPhi}^{-}}\rangle\langle{{\varPhi}^{-}}| + p_{3} |{{\varPsi}^{+}}\rangle\langle{{\varPsi}^{+}}| + (1-(p_{1}+p_{2}+p_{3}))|{{\varPsi}^{-}}\rangle\langle{{\varPsi}^{-}}|, $$

(36)

where the state vectors {|Φ⁺〉,|Φ⁻〉,|Ψ⁺〉,|Ψ⁻〉} denote the Bell basis in the Hilbert space and p₁,p₂,p₃ are probabilities.

The density matrix defined in (36) covers a wide range of particular mixed entangled states, for example the famous Werner state [28].

In order to investigate the problem of quantum tomography, let us first observe that our state ρ(0) can be decomposed in the basis of SU(4) generators:

$$ \begin{aligned} \rho (0) = {}& \frac{1}{4} \mathbb{I}_{4} + \frac{p_{1} - p_{2}}{2} {\varLambda}_{s}^{14} + \frac{1-p_{1}-p_{2} -2p_{3}}{2} {\varLambda}_{s}^{23} + \frac{2p_{1}+2p_{2}-1}{4} {\varLambda}^{1} \\ & + \frac{2p_{1} + 2p_{2} -1}{4 \sqrt{3}} {\varLambda}^{2} + \frac{1-2p_{1} - 2p_{2}}{2\sqrt{6}} {\varLambda}^{3}. \end{aligned} $$

(37)

One is intuitively aware that we need three independent pieces of information in order to reconstruct the density matrix. Thus, one could measure the mean values of three observables from the set of the GGM matrices: ${\varLambda }_{s}^{14}, {\varLambda }_{s}^{23}, {\varLambda }^{1}$ at time instant t = 0, which would give the probabilities p₁,p₂,p₃ required to describe the density matrix. However, we propose a quantum tomography scheme based on the dynamic approach, which leads to a significant improvement. Let us prove a theorem.

Theorem 3

Assuming that the evolution of ρ(0) (prepared as in (36)) is given by a phase-damping channel defined in (22), one can uniquely determine the probabilities p₁,p₂,p₃ (which completely characterize the entangled qubits state) by performing the measurement of one observable Q at three distinct time instants, where

$$ Q = \left [ \begin{array}{cccc} 1 & 0 & 0 & 1 \\0 & -1 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{array} \right]. $$

(38)

Proof

We assume that the evolution of mixed-entangled qubits is subject to the same dynamical map as introduced in (22). Therefore, the decompositions given in (25)–(27) still hold true.

In the case of the observable Q, one can immediately notice that:

$$ \begin{array}{ll} & Q \circ \mathbb{I}_{4} = {\varLambda}^{1}, Q \circ A_{1} = 0, Q \circ A_{2} = 0, Q \circ A_{3} = {\varLambda}_{s}^{14}\\ & Q \circ A_{4} = {\varLambda}_{s}^{23}, Q \circ A_{5} = 0, Q \circ A_{6} = 0, \end{array} $$

(39)

where 0 denotes here the 4 × 4 zero matrix. Then, the formula for the mean value of the observable Q measured at any time instant t_j can be simplified:

$$ m (t_{j}) = \text{ Tr }\{ {\varLambda}^{1} \rho(0)\} + e^{-\gamma_{3} t_{j}} \text{ Tr }\{ {\varLambda}_{s}^{14} \rho(0)\} + e^{-\gamma_{4} t_{j}} \text{ Tr }\{ {\varLambda}_{s}^{23} \rho(0)\}. $$

(40)

Assuming that the mean value of Q can be obtained at three distinct time instants t₁,t₂,t₃, one gets a matrix equation:

$$ \left[ \begin{array}{c} m (t_{1}) \\ m (t_{2}) \\ m (t_{3}) \end{array} \right] = \left[\begin{array}{cccc} 1 & e^{-\gamma_{3} t_{1}} & e^{-\gamma_{4} t_{1}} \\ 1 & e^{-\gamma_{3} t_{2}} & e^{-\gamma_{4} t_{2}} \\ 1 & e^{-\gamma_{3} t_{3}} & e^{-\gamma_{4} t_{3}} \end{array} \right] \left[ \begin{array}{c} \text{ Tr }\{ {\varLambda}^{1} \rho(0)\} \\ \text{ Tr }\{{\varLambda}_{s}^{14} \rho(0)\} \\ \text{ Tr }\{ {\varLambda}_{s}^{23} \rho(0)\} \} \end{array} \right]. $$

(41)

One can compute the expectation values: $\{\text { Tr }\{ {\varLambda }^{1} \rho (0)\}, \text { Tr }\{{\varLambda }_{s}^{14} \rho (0)\}, \text { Tr }\{ {\varLambda }_{s}^{23} \rho (0)\}\}$ on the basis of the experimental data {m(t₁),m(t₂),m(t₃)} if and only if:

$$ \left[\begin{array}{lll} 1 & e^{-\gamma_{3} t_{1}} & e^{-\gamma_{4} t_{1}} \\ 1 & e^{-\gamma_{3} t_{2}} & e^{-\gamma_{4} t_{2}} \\ 1 & e^{-\gamma_{3} t_{3}} & e^{-\gamma_{4} t_{3}} \end{array} \right] \neq 0 $$

(42)

Likewise before, we may assume that the time instants are selected in such a way that they are elements of an arithmetic sequence: t₁ = t, t₂ = 2t, t₃ = 3t. Consequently, the condition (42) can be reformulated:

$$ \det \left[\begin{array}{lll} 1 & \xi_{3} & \xi_{4} \\ 1 & (\xi_{3})^{2} & (\xi_{4})^{2} \\ 1 & (\xi_{3})^{3} & (\xi_{4})^{3} \end{array} \right] \neq 0, $$

(43)

where $\xi _{i} = e^{-\gamma _{i} t}$. One can observe that the rows are linearly independent as long as γ₃≠γ₄. Other decoherence rates does not affect the state of the entangled qubits and for this reason they might be even zeros.

Assuming that γ₃≠γ₄, one can solve (41) and calculate the set of the mean values: $\{\text { Tr }\{ {\varLambda }^{1} \rho (0)\}, \text { Tr }\{{\varLambda }_{s}^{14} \rho (0)\}, \text { Tr }\{ {\varLambda }_{s}^{23} \rho (0)\}\}$, which suffice to determine the probabilities p₁,p₂,p₃ characterizing the initial density matrix. □

The entangled qubits state defined in (36), which is completely characterized by three probabilities {p₁,p₂,p₃}, can be reconstructed from the mean values of one observable measured at three different time instants.

The quantum tomography framework for entangled qubits, which requires only one kind of measurement to reconstruct the initial density matrix, fits well to the current trends in the field. In the context of the dynamic approach to tomography, it has already been discussed that for some specific evolution models one observable is sufficient to determine the initial density matrix [29]. This concept is not only theoretical because experimental realizations have demonstrated recently that a single observable (i.e. one measurement setup) provides all necessary data for quantum state tomography [30]. In quantum process tomography, there is a similar tendency to develop methods which enable to reconstruct unknown quantum channels from few measurements [31].

5 Quantum Tomography of Qudits Subject to Pure Decoherence

5.1 Preliminaries

For a qudit one can always use the generalized Gell-Mann (GGM) basis to decompose any density matrix by means of N² − 1 observables (see details in Appendix). The coefficients which appear in the expansion (53) can be interpreted as the mean values of the GGM operators (they constitute the Bloch vector). Thus, one needs to perform N² − 1 distinct measurements in order to decompose the initial density matrix. This approach seems impractical, especially for higher dimensions since the number of required observables increases quadratically.

5.2 Evolution Model for Qudits

Time evolution of qudits is given by a phase-damping channel according to (1), where the dynamic matrix D(t) is symmetric and shall be expressed as:

$$ D(t) = \left[ \begin{array}{ccccc} 1 & e^{-\gamma_{12} t}& e^{-\gamma_{13} t} & {\cdots} & e^{-\gamma_{1N} t} \\ e^{-\gamma_{12} t} & 1 & e^{-\gamma_{23} t} &{\cdots} & e^{-\gamma_{2N} t} \\ e^{-\gamma_{13} t} & e^{-\gamma_{23} t} & 1 & {\dots} &e^{-\gamma_{3N} t}\\ {\vdots} & {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ e^{-\gamma_{1N} t} & e^{-\gamma_{2N} t} & e^{-\gamma_{3N} t} &{\cdots} & 1 \end{array} \right], $$

(44)

where we assume that no two decoherence rates are the same.

5.3 Results and Analysis

We shall investigate what can be said about the benefits of the dynamic approach to quantum tomography of systems subject to pure decoherence. We formulate two theorems – one tells about the advantages of the dynamic tomography, whereas the other indicates a serious limitation of this method. The first theorem demonstrates that one can in general very efficiently obtain the off-diagonal elements of the density matrix. On the other hand, the latter describes the worst-case scenario which is connected with computing the diagonal part of the unknown matrix. The theorem gives the formula for the upper limit of the number of distinct observables required for quantum tomography.

Theorem 4

For a qudit subject to pure decoherence with the dynamic matrix defined in (44) one can reconstruct all off-diagonal elements of the unknown density matrix ρ(0) from the mean values of two observables measured at $\frac {N(N-1)}{2}+1$ distinct time instants.

Proof

Let us start by representing D(t) as:

$$ D(t) = \mathbb{I}_{N} + \sum\limits_{j=1}^{N-1} \sum\limits_{k=j+1}^{N} e^{-\gamma_{jk}t} A_{jk}, $$

(45)

where A_jk = E_jk + E_kj and E_jk denotes a matrix from the standard basis.

Now, we define 2 observables by means of the GGM matrices (see Appendix):

$$ \begin{array}{ll} & Q_{1} = {\varLambda}^{1} + \sum\limits_{i=1}^{\kappa_{1}(N)} \sum\limits_{k= 2i}^{N} {\varLambda}_{s}^{(2i-1)k} + \sum\limits_{i=1}^{\kappa_{2}(N)} \sum\limits_{k= 2i+1}^{N} {\varLambda}_{a}^{(2i)k},\\ & Q_{2} = {\varLambda}^{2} + \sum\limits_{i=1}^{\kappa_{2}(N)} \sum\limits_{k= 2i+1}^{N} {\varLambda}_{s}^{(2i)k} + \sum\limits_{i=1}^{\kappa_{1}(N)} \sum\limits_{k= 2i}^{N} {\varLambda}_{a}^{(2i-1)k}, \end{array} $$

(46)

where

$$ \begin{array}{ll} & \kappa_{1} (N) = \begin{cases} \frac{N-1}{2} &\text{ when } N \text{ is odd} \\ \frac{N}{2} &\text{ when } N \text{ is even} \end{cases}\\ &\kappa_{2} (N) = \begin{cases} \frac{N-1}{2} &\text{ when } N \text{ is odd} \\ \frac{N-2}{2} &\text{ when } N \text{ is even} \end{cases}. \end{array} $$

(47)

Then, for any time instant t_j, the mean values of Q₁ and Q₂ can be written as:

$$ \begin{aligned} m_{1} (t_{j}) = \text{ Tr } \{{\varLambda}^{1} \rho(0)\} &{}+ \sum\limits_{i=1}^{\kappa_{1}(N)} \sum\limits_{k= 2i}^{N} e^{-\gamma_{(2i-1)k}t_{j}} \text{ Tr }\{{\varLambda}_{s}^{(2i-1)k} \rho(0)\} \\& +\sum\limits_{i=1}^{\kappa_{2}(N)} \sum\limits_{k= 2i+1}^{N} e^{-\gamma_{(2i)k}t_{j}} \text{ Tr }\{{\varLambda}_{a}^{(2i)k} \rho(0)\} \end{aligned} $$

(48)

$$ \begin{aligned} m_{2} (t_{j}) = \text{ Tr } \{{\varLambda}^{2} \rho(0)\}&{} + \sum\limits_{i=1}^{\kappa_{2}(N)} \sum\limits_{k= 2i+1}^{N} e^{-\gamma_{(2i)k}t_{j}} \text{ Tr }\{{\varLambda}_{s}^{(2i)k} \rho(0)\} \\&+ \sum\limits_{i=1}^{\kappa_{1}(N)} \sum\limits_{k= 2i}^{N} e^{-\gamma_{(2i-1)k}t_{j}} \text{ Tr }\{{\varLambda}_{a}^{(2i-1)k} \rho(0)\} \end{aligned} $$

(49)

One can notice that if we measure both observables at $\frac {N(N-1)}{2}+1$ time instants selected in such a way that t₁ = t, t₂ = 2t, $t_{3} = 3 t, \dots$ then from (48)-49 we can compute the mean values of N(N − 1) + 2 observables: i.e. the $\frac {N(N-1)}{2}$ symmetric GGM, the $\frac {N(N-1)}{2}$ antisymmetric GGM and the two diagonal GGM Λ¹ and Λ². This means that the measurements provide N(N − 1) + 2 independent pieces of information which are sufficient to determine the off-diagonal elements of the density matrix. □

Theorem 5

For a qudit subject to pure decoherence with evolution governed by a dynamic matrix defined in (44) the upper boundary of the number of distinct observables required for state reconstruction equals: N − 1.

Proof

We obtain complete knowledge about the off-diagonal elements of the density matrix on the basis of the mean values of the operators from (46). However, the dynamic approach does not give any advantage when it comes to the diagonal elements since a phase-damping channel does not affect the diagonal of ρ(0). Therefore, in the worst-case scenario, one would additionally need to measure the mean values of the remaining N − 3 diagonal GGM matrices at time instant t = 0, which means that finally one would use N − 1 distinct observables to reconstruct the density matrix. The final formula for the initial state could be written according to (53). □

For specific qudits, the minimal number of distinct observables might be lower than N − 1 since one may a priori know that there are some zeros on the diagonal of ρ(0).

6 Conclusions

In this article we have proved that the dynamic approach to quantum tomography can be an effective method of state reconstruction for qutrits and entangled qubits which are sent through phase-damping channels. Assuming that the knowledge about evolution is given, one can switch to the Heisenberg representation and define the measurements in time domain. The results are in line with recent developments in quantum tomography where there is a tendency to search for methods that aim to reduce the number of distinct types of measurement involved in state reconstruction [32,33,34].

In conclusion, we have formulated general theorems concerning the criteria for quantum tomography of qudits. The first theorem describes the optimal benefits that one can obtain from applying this approach, i.e. all off-diagonal elements of a density matrix can be computed from the mean values of two observables; whereas the other theorem expresses a key limitation of the method. If the system is subject to pure decoherence, then in the worst-case scenario, one needs N − 1 distinct observables to reconstruct the initial state. These theorems appear to have closed up the topic of the quantum state tomography of systems subject to pure decoherence.

Appendix: Generalized Gell-Mann Matrices

In general, all GGM matrices can be divided into 3 groups and for $\dim {\mathscr{H}} =N$ they are defined as [24, 26]:

i) $\frac {N(N-1)}{2}$ symmetric GGM matrices

$$ {\varLambda}_{s}^{jk} = |{j}\rangle\langle{k}| + |{k}\rangle\langle{j}|, 1 \leq j < k \leq N, $$

(50)

ii) $\frac {N(N-1)}{2}$ antisymmetric GGM matrices

$$ {\varLambda}_{a}^{jk} = -i |{j}\rangle\langle{k}| + i |{k}\rangle\langle{j}|, 1 \leq j < k \leq N, $$

(51)

iii) (N − 1) diagonal GGM matrices

$$ \begin{array}{@{}rcl@{}} {\varLambda}^{l} &=& \sqrt{\frac{2}{l(l+1)}} \left( \sum\limits_{j=1}^{l} |{j}\rangle\langle{j}| - l|{l+1}\rangle\langle{l+1}| \right),\\ &&1 \leq l \leq N-1, \end{array} $$

(52)

where |k〉,|j〉,|l〉 denote vectors from the standard basis.

One can notice that in total we have N² − 1 GGM matrices. From the definitions we can see that all GGM matrices are traceless and self-adjoint. It can be proved that they are orthogonal and form a basis. Thus, they are the generators of SU(N).

A density matrix associated with a Hilbert space such that $\dim {\mathscr{H}} =N$ can be decomposed according to [24]:

$$ \rho = \frac{1}{N} \mathbb{I}_{N} + \frac{1}{2} \mathbf{s} \cdot \hat{{\varLambda}}, $$

(53)

where s denotes the Bloch vector and $\hat {{\varLambda }}$ the vector generated from ordered GGM matrices. The elements of the Bloch vector are equal to the mean values of the corresponding GGM operators.