The Precision of Parameter Estimation for Dephasing Model Under Squeezed Reservoir

Abstract

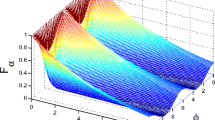
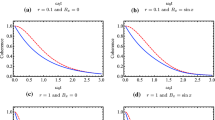
We study the precision of parameter estimation for dephasing model under squeezed environment. We analytically calculate the dephasing factor γ(t) and obtain the analytic quantum Fisher information (QFI) for the amplitude parameter α and the phase parameter ϕ. It is shown that the QFI for the amplitude parameter α is invariant in the whole process, while the QFI for the phase parameter ϕ strongly depends on the reservoir squeezing. It is shown that the QFI can be enhanced for appropriate squeeze parameters r and θ. Finally, we also investigate the effects of temperature on the QFI.

Appendix: Derive the dephasing factor γ(t)

In this section, we will derive the dephasing factor γ(t) (12) in the dephasing processing under the squeezed vacuum reservoir. In the interaction picture, the interaction Hamiltonian can be written as

$$\begin{array}{@{}rcl@{}} H_{\mathrm{I}}(t) &=&e^{iH_{0}t}H_{\mathrm{I}}e^{-iH_{0}t} \\ &=&\sum\limits_{k}g_{k}\sigma_{z}(b_{k}^{\dagger }e^{i\omega_{k}t}+b_{k}e^{-i\omega_{k}t}). \end{array} $$

(A1)

According to the Magnus expression [33], the unitary time-evolution operator in the interaction picture can be given by

$$\begin{array}{@{}rcl@{}} U(t) &=&\mathrm{T}_{\leftarrow }\exp \left[ -i{{\int}_{0}^{t}}dt^{\prime }H_{ \mathrm{I}}(t^{\prime })\right] \\ &=&C(t)\cdot V(t), \end{array} $$

(A2)

wherethetime-dependent complex number C(t) is given by $C(t) = \exp \left [{\sum }_{k}{g_{k}^{2}}\frac {\sin (\omega _{k}t)-\omega _{k}t}{i{\omega _{k}^{2}}}\right ]$, and the unitary operator V(t) is defined as $V(t) = \exp \left [ \sigma _{z}{\sum }_{k}\left (\alpha _{k}b_{k}^{\dagger }-\alpha _{k}^{\ast }b_{k}\right ) \right ]$ with the amplitude coefficient $\alpha _{k}=g_{k}\frac {1-e^{i\omega _{k}t}}{\omega _{k}}$.

The initial state of the system plus the environment is assumed to be a product state ρ _s(0)⊗ρ _bath. Due to the communication between the system’s Hamiltonian $\frac {\sigma _{z}\omega _{k}}{2}$ and the interaction Hamiltonian ${\sum }_{k}g_{k}\sigma _{z}(b_{k}+b_{k}^{\dagger })$, the evolution of the reduced density matrix element for dephasing processing under squeezed vacuum reservoir is governed by [8]

$$\begin{array}{@{}rcl@{}} \rho_{ij}\left( t\right) = \left\langle i\right\vert \text{Tr}_{\mathrm{ bath}}\left\{ V(t)\rho_{s}(0)\otimes \rho_{\text{bath} }V^{\dagger}(t)\right\} \left\vert j\right\rangle. \end{array} $$

(A3)

In the above equation, the time-dependent complex number C(t) multiplied by its complex conjugation is equal to unit, so it can be omitted. For the diagonal elements of the reduced density matrix, it is easy to prove that the elements do not evolute, i.e., ρ ₁₁(t) = ρ ₁₁(0) and ρ ₀₀(t) = ρ ₀₀(0).

Then, we will characterize the dynamics of the off-diagonal elements going through the dephasing process under the squeezed vacuum reservoir. Substituting V(t) into (A3), the evolution of the element ρ ₁₀(t) can be given as follows

$$\begin{array}{@{}rcl@{}} \rho_{10}\left( t\right) &=&\text{Tr}_{\text{bath}}\left\{ \exp \left[ \sum\limits_{k}2(\alpha_{k}b_{k}^{\dagger }-\alpha_{k}^{\ast }b_{k}) \right] \rho_{\text{bath}}\right\} \rho_{10}(0) \\ &=&\prod\limits_{k^{\prime }}\langle 0_{k^{\prime }}\vert S_{k^{\prime }}^{\dagger }\exp [ \sum\limits_{k}2(\alpha_{k}b_{k}^{\dagger }-\alpha_{k}^{\ast }b_{k}) ] S_{k^{\prime }}\vert 0_{k^{\prime }}\rangle \rho_{10}(0) \\ &=&\exp [ -\sum\limits_{k}2\vert \beta_{k}\vert^{2}] \rho_{10}(0), \end{array} $$

(A4)

where the complex number coefficient $\beta _{k}=\alpha _{k}\cosh r+e^{i\theta }\alpha _{k}^{\ast }\sinh r$.

We can define the parameter ${\sum }_{k}2\left \vert \beta _{k}\right \vert ^{2}$ being the dephasing factor γ(t),

$$\begin{array}{@{}rcl@{}} \gamma (t) \sum\limits_{k}\left\vert \alpha_{k}\right\vert^{2}\left[ 2\cosh (2r)+\left( {\alpha_{k}^{2}}e^{-i\theta }+\alpha_{k}^{\ast 2}e^{i\theta }\right) \sinh (2r)\right] .\\ \end{array} $$

(A5)

So the evolution of the element ρ ₁₀(t) is governed by

$$\begin{array}{@{}rcl@{}} \rho_{10}(t) =\exp [-\gamma (t)]\rho_{10}(0) =\rho_{01}(t)^{\ast }. \end{array} $$

(A6)

Substituting the amplitude coefficient α _k in the time-evolution operator U(t) into the dephasing factor γ(t), we can obtain the analytic expression for the dephasing factor as

$$\begin{array}{@{}rcl@{}} \gamma (t) = \sum\limits_{k}4{g_{k}^{2}}\frac{1-\cos \omega_{k}t}{{\omega_{k}^{2}}} \left[ \cosh (2r)-\cos (\omega_{k}t-\theta )\sinh (2r)\right] .\\ \end{array} $$

(A7)

Considering the spectrum density J(ω) of the modes for the frequency ω [8] as J(ω) = 4f(ω)|g(ω)|², performing the continuum limit of the reservoir modes and changing the sum on k in (A7) to the integral on the frequency ω, we can obtain the dephasing factor γ(t) in (10).