Hermite Polynomial’s Photon Added Coherent State and its Non-classical Properties

Abstract

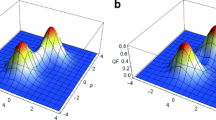
In this paper, we will present the Hermite polynomial’s photon added coherent state (HPPACS), which can be obtained by superposing the photon-added coherent states(PACS) in the form of Hermite polynomial . Some quantum statistical properties of the introduced HPPACS, such as the Q-function, photon-number distribution, etc., are investigated. Meanwhile, we also give some profound squeezing properties of the HPPACS through its position distribution, quadrature squeezing and the degree of squeezing. Finally, the fidelity between the squeezed coherent state (SCS) and the HPPACS will be investigated numerically.

Appendices

Appendix A: Derivation of (18) and (19)

Using the generating function of Hermite polynomials

$$ H_{m} \left( x \right)=\left. {\frac{\partial^{m}}{\partial t^{m}}\exp \left( {2xt-t^{2}} \right)} \right|_{t=0} , $$

(A1)

we have

$$ H_{m} \left( {a^{\dag }} \right)=\left. {\frac{\partial^{m}}{\partial t^{m}}\exp \left( {2a^{\dag }t-t^{2}} \right)} \right|_{t=0} . $$

(A2)

Using the operator formula

$$ e^{Aa}f\left( {a^{\dag }} \right)e^{-Aa}=\sum\limits_{n=0}^{\infty} \,\frac{A^{n}}{n!}f^{\left( n \right)}\left( {a^{\dag }} \right)=f\left( {a^{\dag }+A} \right), $$

(A3)

and the recursion formula of Hermite polynomials in (6), we have

$$\begin{array}{@{}rcl@{}} H_{m} \left( a \right)a^{\dag } & =&\left. {\frac{\partial^{m}}{\partial t^{m}}\exp \left( {2at-t^{2}} \right)a^{\dag }} \right|_{t=0} \\ & =&\left. {\frac{\partial^{m}}{\partial t^{m}}\left( {a^{\dag }+2t} \right)\exp \left( {2at-t^{2}} \right)} \right|_{t=0} \\ & =&\left. {\frac{\partial^{m}}{\partial t^{m}}a^{\dag }\exp \left( {2at-t^{2}} \right)} \right|_{t=0} +\left. {\frac{\partial^{m}}{\partial t^{m}}2t\exp \left( {2at-t^{2}} \right)a^{\dag }} \right|_{t=0} \\ & =&a^{\dag }H_{m} \left( a \right)+2mH_{m-1} \left( a \right). \end{array} $$

(A4)

Using the method similar to those above, one finds

$$ aH_{m} \left( {a^{\dag }} \right)=H_{m} \left( {a^{\dag }} \right)a+2mH_{m-1} \left( {a^{\dag }} \right). $$

(A5)

With the help of (A4) and (A5), we obtain the average value of a ^† a

$$\begin{array}{@{}rcl@{}} \left\langle {a^{\dag }a} \right\rangle & =&N_{m}^{^{-1}} \langle \alpha \left|\right.\left[ {a^{\dag }H_{m} \left( a \right)+2mH_{m-1} \left( a \right)} \right]\left[ {H_{m} \left( {a^{\dag }} \right)a+2mH_{m-1} \left( {a^{\dag }} \right)} \right]\left|\alpha \right\rangle \\ & =&N_{m}^{-1} \langle \alpha \left|\right.\left[ {\left| {\alpha^{2}} \right|H_{m} \left( a \right)H_{m} \left( {a^{\dag }} \right)+2m\alpha^{\ast }H_{m} \left( a \right)H_{m-1} \left( {a^{\dag }} \right)} \right. \\ &+&\left.2m\alpha H_{m-1} \left( a \right)H_{m} \left( {a^{\dag }} \right)+4m^{2}H_{m-1} \left( a \right)H_{m-1} \left( {a^{\dag }} \right) \right]\left| \alpha\right\rangle\\ &=&\left| {\alpha^{2}} \right|+4m^{2}\frac{N_{m-1} }{N_{m} }+2m\frac{1}{N_{m} }\left( {\alpha^{\ast }L_{m,m-1} +\alpha L_{m-1,m} } \right), \end{array} $$

(A6)

where the symbol L _{n, m} denotes the average value of 〈α|H _{n, m} |α〉 in(8).

Appendix B: Derivation of (22)

Using (A2) and the integration formula

$$ \int \frac{d^{2}z}{\pi }\exp \left( -\left| z \right|^{2} +\sigma z+\eta z^{\ast } \right)=\exp \left( {\sigma \eta } \right), $$

(B1)

we have

$$\begin{array}{@{}rcl@{}} W\left( {\gamma ,\gamma^{\ast }} \right) & =&\frac{2e^{2\left| \gamma \right|^{2} }}{\pi }N_{m}^{-1} \int \frac{d^{2}\lambda }{\pi }H_{m} \left( {-\lambda^{\ast }} \right)H_{m} \left( \lambda \right)\exp \\ &&\quad \left[-\left| \lambda \right|^{2} -\left| \alpha \right|^{2} +\left( {\alpha^{\ast }-2\gamma^{\ast }} \right)\lambda +\left( {2\gamma -\alpha } \right)\lambda^{\ast }\right]\\ &=&\frac{2e^{2\left| \gamma \right|^{2} }}{\pi }N_{m}^{-1} \frac{\partial^{2m}}{\partial t^{m}\partial t^{^{\prime }m}}\smallint \frac{d^{2}\lambda }{\pi }\exp\\ &&\times \left.\left[ {-\left| \lambda \right|^{2} -\left| \alpha \right|^{2} +\left( {\alpha^{\ast }-2\gamma^{\ast }+2t^{\prime }} \right)\lambda +\left( {2\gamma -\alpha -2t} \right)\lambda^{\ast }-t^{\prime 2}-t^{2}} \right] \right|_{t=t^{\prime }=0} \\ & =&\frac{2}{\pi }\exp \left[ {-2\left( {\left| \gamma \right|^{2} +\left| \alpha \right|^{2} -\gamma \alpha^{\ast }-\alpha \gamma^{\ast }} \right)} \right] \frac{\partial^{2m}}{\partial t^{m}\partial t^{^{\prime }m}}\exp\\ &&\times\left.\left[ {-t^{\prime 2}+\left( {4\gamma -2\alpha -4t} \right)t^{\prime }-2\left( {\alpha^{\ast }-2\gamma^{\ast }} \right)t-t^{2}} \right] \right|_{t=t^{\prime }=0}\\ & =&\frac{2}{\pi }N_{m}^{-1} \exp \left[ {-2\left( {\left| \gamma \right|^{2} +\left| \alpha \right|^{2} -\gamma \alpha^{\ast }-\alpha \gamma^{\ast }} \right)} \right] \frac{\partial^{m}}{\partial t^{m}}H_{m} \left( {2\gamma -\alpha -2t} \right)\exp\\ &&\times\left.\left[ {-2t\left( {\alpha^{\ast }-2\gamma^{\ast }} \right)-t^{2}} \right] \right|_{t=0} . \end{array} $$

(B2)

Appendix C: Derivation of (25)

Noting the wave function of the coherent state

$$ \left\langle q \right.\left| \beta\right\rangle =\pi^{-1/4}\exp \left( {-\frac{1}{2}q^{2}+\sqrt 2 q\beta -\frac{1}{2}\beta^{2}-\frac{1}{2}\left| \beta \right|^{2} } \right), $$

(C1)

and usint the complteness of the coherent state, we first calculate the wave function of the HPPACS as

$$\begin{array}{@{}rcl@{}} W_{H} &=&N_{m}^{-1/2} \pi^{-1/4}\exp \left( {-\frac{1}{2}\left| \alpha \right|^{2} -\frac{1}{2}q^{2}} \right)\int \frac{d^{2}\beta }{\pi }H_{m} \left( {\beta^{\ast }} \right)\exp \left( {-\left| \beta \right|^{2} +\sqrt 2 q\beta +\alpha \beta^{\ast }-\frac{\beta^{2}}{2}} \right) \\ & =&N_{m}^{-1/2} \pi^{-1/4}\exp \left( {-\frac{1}{2}\left| \alpha \right|^{2} -\frac{1}{2}q^{2}} \right) \frac{\partial^{m}}{\partial t^{m}}\exp \left( {-t^{2}} \right)\int \frac{d^{2}\beta }{\pi }\exp\\ &&\left.\left[ {-\left| \beta \right|^{2} -\frac{\beta^{2}}{2}+\left( {2t+\alpha } \right)\beta^{\ast }+\sqrt 2 q\beta } \right] \right|_{t=0} \\ & =&N_{m}^{-1/2} \pi^{-1/4}\exp \left( {-\frac{1}{2}\left| \alpha \right|^{2} -\frac{1}{2}\alpha^{2}-\frac{q^{2}}{2}+\sqrt 2 q\alpha } \right)\left. {\frac{\partial^{m}}{\partial t^{m}}\exp \left[ {-3t^{2}+2\left( {\sqrt 2 q-\alpha } \right)t} \right]} \right|_{t=0} \\ & =&-N_{m}^{-1/2} \pi^{-1/4}\sqrt{3}^{m} \exp \left( {-\frac{1}{2}\left| \alpha \right|^{2} -\frac{1}{2}\alpha^{2}-\frac{q^{2}}{2}+\sqrt 2 q\alpha} \right)H_{m} \left( {\frac{\alpha }{\sqrt{3} }-\sqrt {\frac{2}{3}} q} \right), \end{array} $$

(C2)

where we have used

$$\begin{array}{@{}rcl@{}} \left. {\frac{\partial^{n}}{\partial t^{n}}\exp \left( {At+Bt^{2}} \right)} \right|_{t=0} =\left( {i\sqrt{B} } \right)^{n} H_{n} \left( {\frac{A}{2i\sqrt{B} }} \right), \end{array} $$

(C3)

and the integral formula

$$\begin{array}{@{}rcl@{}} &&\smallint \frac{d^{2}z}{\pi }\exp \left( {\zeta \left| z \right|^{2} +\xi z+\eta z^{\ast}+fz^{2}+gz^{\ast 2}} \right)\\ &&=\frac{1}{\sqrt{\zeta^{2}-4fg} }\exp \left[ {\frac{-\zeta \xi \eta +\xi ^{2}g+\eta^{2}f}{\zeta^{2}-4fg}} \right], \end{array} $$

(C4)

whose convergent condition is $Re\left ({\xi +f+g} \right )<0,Re\left (\frac {\zeta ^{2}-4fg} {\xi +f+g} \right )<0,$or $Re\left (\xi -f-g \right )<0, \quad Re\left (\frac {\zeta ^{2}-4fg} {\xi -f-g} \right )<0.$

Substituting Eq. (C2) into (23) , one have

$$\begin{array}{@{}rcl@{}} W_{q} =N_{m}^{-1} \pi^{-1/2}3^{m}\exp \left( {-\left| \alpha \right|^{2} -\alpha^{2}-q^{2}+2\sqrt 2 q\alpha } \right)\left| {H_{m} \left( {\frac{\alpha }{\sqrt 3 }-\sqrt{\frac{2}{3}} q} \right)} \right|^{2} . \end{array} $$

(C5)

Appendix D: The Average Value of Some Operators

Using the similar way in appendix A, we have

$$\begin{array}{@{}rcl@{}} H_{m} \left( a \right)a^{\dag 2}=a^{\dag 2}H_{m} \left( a \right)+4m\left( {m-1} \right)H_{m-2} \left( a \right)+4ma^{\dag }H_{m-1} \left( a \right) \end{array} $$

(D.1)

and the average value of a ^†2 is

$$ \left\langle {a^{\dag 2}} \right\rangle =\alpha^{\ast 2}+4m\alpha^{\ast }\frac{L_{m-1,m} }{N_{m} }+4m\left( {m-1} \right)\frac{L_{m-2,m} }{N_{m} }, $$

(D.2)

$$ \left\langle {a^{2}} \right\rangle =\alpha^{2}+4m\alpha \frac{L_{m,m-1}}{N_{m} }+4m\left( {m-1} \right)\frac{L_{m,m-2} }{N_{m} }. $$

(D.3)

Similarly, we calculate

$$ \left\langle a \right\rangle =\alpha +2m\frac{L_{m,m-1} }{N_{m} }, $$

(D.4)

and

$$ \left\langle {a^{\dag }} \right\rangle =\alpha^{\ast }+2m\frac{L_{m-1,m} }{N_{m} }. $$

(D.5)

Appendix E: Derivation of (33)

To get the explicit form of (33), we first calculate the following overlap $\langle \alpha |H_{m} \left (a \right )S\left (\lambda \right )\left | \alpha \right \rangle$ by using (32) as

$$\begin{array}{@{}rcl@{}} && \langle \alpha \left|\right.H_{m} \left( a \right)S\left( \lambda \right)\left| \alpha\right\rangle \\ && =sech^{1/2} \lambda \exp \left( {\frac{\alpha^{2}}{2}\tanh \lambda } \right) \frac{\partial^{m}}{\partial t^{m}}\exp \left( {-t^{2}} \right)\langle \alpha \left|\right.\exp \left( {2at} \right)\exp \\ &&\qquad \times\left.\left( {-\frac{a^{\dag 2}}{2}\tanh \lambda } \right)\exp \left[ {\left( {sech\lambda -1} \right)a^{\dag }\alpha } \right]\left| \alpha\right\rangle \right|_{t=0} \\ && =sech^{1/2} \lambda \exp \left( {\frac{\alpha^{2}}{2}\tanh \lambda -\frac{\alpha^{\ast 2}}{2}\tanh \lambda } \right) \\ &&\left. {\frac{\partial^{m}}{\partial t^{m}}\exp \left[ {-t^{2}\left( {1+2\tanh \lambda } \right)-2t\alpha^{\ast }\tanh \lambda +2t\left( {sech\lambda -1} \right)\alpha +\left( {sech\lambda -1} \right)\left| \alpha \right|^{2} +2\alpha t} \right]} \right|_{t=0} \\ &&=sech^{1/2} \lambda \exp \left( {\frac{\alpha^{2}}{2}\tanh \lambda -\frac{\alpha^{\ast 2}}{2}\tanh \lambda +\left( {sech\lambda -1} \right)\left| \alpha \right|^{2} } \right) \frac{\partial^{m}}{\partial t^{m}}\exp\\ &&\qquad\times\left.\left[ {-t^{2}\left( {1+2\tanh \lambda } \right)+2t\left( {\alpha sech\lambda -\alpha^{\ast }\tanh \lambda } \right)} \right] \right|_{t=0} \\ &&=sech^{1/2} \lambda {F_{2}^{n}} \exp \left( {F_{1}} \right)H_{m} \left( {F_{3} } \right), \end{array} $$

(E1)

where

$$F_{1} =\left( {sech\lambda -1} \right)\left| \alpha \right|^{2} +\frac{1}{2}\left( {\alpha^{2}-\alpha^{\ast 2}} \right)\tanh \lambda , $$

$$F_{2} =-\sqrt {1+2\tanh \lambda } , $$

$$F_{3} =\frac{2\left( {\alpha sech\lambda -\alpha^{\ast }\tanh \lambda } \right)}{-2\sqrt {1+2\tanh \lambda } }. $$

and we also used the following operator identical

$$ e^{\xi a}e^{\eta a^{\dag 2}}=e^{\eta a^{\dag 2}}e^{2\xi \eta a^{\dag }}e^{\xi a}e^{\xi^{2}\eta }, $$

and

$$ e^{A}e^{B}=e^{B}e^{A}e^{[A,B]} $$

in the case [A,[A, B]]=[B,[A, B]]=0.

Substituting (E1) into (31), we have the result in (33)