An Infinite Family of Magnetized Morgan-Morgan Relativistic Thin Disks

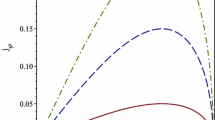
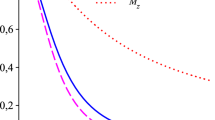
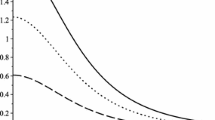
Abstract

Applying the Horský-Mitskievitch conjecture to the empty space solutions of Morgan and Morgan due to the gravitational field of a finite disk, we have obtained the corresponding solutions of the Einstein-Maxwell equations. The resulting expressions are simply written in terms of oblate spheroidal coordinates and the solutions represent fields due to magnetized static thin disk of finite extension. Now, although the solutions are not asymptotically flat, the masses of the disks are finite and the energy-momentum tensor agrees with the energy conditions. Furthermore, the magnetic field and the circular velocity show an acceptable physical behavior.

Appendix

We pass on to the definition of the Hodge ^⋆ (star) operation. Let’s us M a m-dimensional manifold endowed with a metric g. The Hodge ^⋆ (star) operation is a map: Ω ^r(M)→Ω ^r−m(M) whose action, on the basis of the vector Ω ^r(M), is defined by [54]

$$\boldsymbol{^{\star}}(\boldsymbol{dx}^{\mu_1}\wedge\boldsymbol{dx}^{\mu_2}\wedge\ldots\wedge \boldsymbol{dx}^{\mu_r})=\frac{\sqrt{|g|}}{(m-r)!}\varepsilon^{{\mu_1}{\mu_2}\ldots{\mu_r}}_{\qquad{\mu_{r+1}}\ldots{\mu_m}}\boldsymbol{dx}^{\mu_{r+1}}\wedge\ldots\wedge \boldsymbol{dx}^{\mu_m}.$$

For a r-form

$$\boldsymbol{A} = \frac{1}{r!}A_{{\mu_1}{\mu_2}\ldots{\mu _r}}\boldsymbol{dx}^{\mu_1}\wedge\boldsymbol{dx}^{\mu_2}\wedge\ldots\wedge \boldsymbol{dx}^{\mu_r}\in\varOmega^r$$

we have

$$\boldsymbol{^{\star} A} = \frac{\sqrt{|g|}}{r!(r-m)!}A_{{\mu_1}{\mu_2}\ldots{\mu_r}}\varepsilon^{{\mu_1}{\mu_2}\ldots{\mu_r}}_{\qquad{\mu_{r+1}}\ldots{\mu_m}}\boldsymbol{dx}^{\mu_{r+1}}\wedge\ldots \wedge\boldsymbol{dx}^{\mu_m}\in\varOmega^{m-r},$$

where the totally anti-symmetric tensor ε is

$$\varepsilon_{\mu_1\mu_2\ldots\mu_m} =\begin{cases}+ 1\quad\mbox{if}\ (\mu_1\mu_2\ldots\mu_m)\\\quad \mbox{is an even permutation of}\ (12\ldots m),\\{-} 1\quad \mbox{if}\ (\mu_1\mu_2\ldots\mu_m)\\\quad \mbox{is an odd permutation of}\ (12\ldots m),\\\quad0\quad \mbox{otherwise},\end{cases}$$

and “∧” is the usual exterior product or wedge product.