Unsteady Flow of Radiating and Chemically Reacting MHD Micropolar Fluid in Slip-Flow Regime with Heat Generation

Abstract

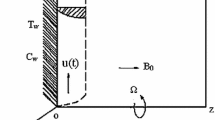
An analytical study of the problem of unsteady free convection with thermal radiation and heat generation on MHD micropolar fluid flow through a porous medium bounded by a semi-infinite vertical plate in a slip-flow regime has been presented. The Rosseland diffusion approximation is used to describe the radiation heat flux in the energy equation. The homogeneous chemical reaction of first order is accounted for in the mass diffusion equation. A uniform magnetic field acts perpendicular on the porous surface absorbing micropolar fluid with a suction velocity varying with time. A perturbation technique is applied to obtain the expressions for the velocity, microrotation, temperature, and concentration distributions. Expressions for the skin-friction, Nusselt number, and Sherwood number are also obtained. The results are discussed graphically for different values of the parameters entered into the equations of the problem.

Appendix

The exponential indices in Eqs. 34–41 are defined by

$$\begin{aligned} h_{1}&= \frac{1}{2(1+\beta )}\left[ 1+\sqrt{1+4N(1+\beta )}\right] , \\ \ h_{2}&= \frac{1}{2(1+\beta )}\left[ 1+\sqrt{1+4(\delta +N)(1+\beta )} \right] , \\ h_{3}&= \frac{\mathrm{3Pr}}{2(3+4R)}\left[ 1+\sqrt{1+\frac{4(\delta -H)(3+4R)}{\mathrm{3Pr}}} \right] , \\ \ h_{4}&= \frac{Sc}{2}\left[ 1+\sqrt{1+\frac{4(\delta +K_{c})}{Sc}}\right] , \\ h_{5}&= \frac{\eta }{2}\left[ 1+\sqrt{1+\frac{4\delta }{\eta }}\right] , \\ h_{6}&= \frac{Sc}{2}\left[ 1+\sqrt{1+\frac{4K_{c}}{Sc}}\right] , \\ R_{1}&= \frac{\mathrm{3Pr}}{2(3+4R)}\left[ 1+\sqrt{1-\frac{4H(3+4R)}{\mathrm{3Pr}}}\right] , \end{aligned}$$

and the coefficients are given by

$$\begin{aligned} Z_{1}&= \frac{3A Pr R_{1}}{(3+4R)R_{1}^{2}-3 Pr R_{1}-3(\delta -H) Pr}, \\ a_{1}&= \frac{h_{1}}{1+hh_{1}}, \\ a_{2}&= \frac{Gr}{(1+\beta )R_{1}^{2}-R_{1}-N}, \\ a_{3}&= \frac{Gc}{(1+\beta )h_{6}^{2}-h_{6}-N}, \\ a_{4}&= \frac{2\beta \eta b_{1}}{(1+\beta )\eta ^{2}-\eta -N}=X_{1}b_{1}, \\ b_{1}&= \frac{na_{1}}{1+nX_{1}\left( a_{1}(1+\eta h)-\eta \right) }\left( a_{2}(1+R_{1}h)+a_{3}(1+hh_{6})-1\right. \\&\left. -\frac{1}{a_{1}}(a_{2}R_{1}+a_{3}h_{6}) \right) , \\ b_{2}&= \frac{1}{1\!+\!nK_{1}X_{2}}\left[ n(h_{2}t_{4}t_{5}\!-\!h_{2}t_{4}t_{7}\!+\!h_{3}d_{1}d_{4}h_{4}\!-\!d_{12}h_{6}\!-\!d_{11}R_{1}\!+\!h_{1}d_{7}\!-\!d_{13}\eta )\right. \\&\left. + \frac{Ab_{1}\eta }{\delta }\right] , \\ b_{4}&= \frac{A Sc h_{6}}{h_{6}^{2}-Sch_{6}-(\delta +K_{c})Sc}, \\ b_{6}&= \frac{1}{1+hh_{1}}\left[ a_{2}(1+R_{1}h)+a_{3}(1+hh_{6})-a_{4}(1+ \eta h)-1\right] , \\ d_{1}&= \frac{Gr(Z_{1}-1)}{(1+\beta )h_{3}^{2}-h_{3}-(\delta +N)}, \\ d_{2}&= \frac{AR_{1}a_{2}}{(1+\beta )R_{1}^{2}-R_{1}-(\delta +N)}, \\ d_{3}&= \frac{Grb_{4}}{(1+\beta )h_{6}^{2}-h_{6}-(\delta +N)}, \\ d_{4}&= \frac{Gc(b_{4}-1)}{(1+\beta )h_{4}^{2}-h_{4}-(\delta +N)}, \\ d_{5}&= \frac{2\beta b_{2}h_{5}}{(1+\beta )h_{5}^{2}-h_{5}-(\delta +N)} =X_{2}b_{2}, \\ d_{6}&= \frac{2\beta \eta ^{2}Ab_{1}}{\delta \left[ (1+\beta )\eta ^{2}-\eta -(\delta +N)\right] }, \\ d_{7}&= \frac{Ah_{1}b_{6}}{(1+\beta )h_{1}^{2}-h_{1}-(\delta +N)}, \\ d_{8}&= \frac{GrZ_{1}}{(1+\beta )R_{1}^{2}-R_{1}-(\delta +N)}, \\ d_{9}&= \frac{Ah_{6}a_{3}}{(1+\beta )h_{6}^{2}-h_{6}-(\delta +N)}, \\ d_{10}&= \frac{A\eta a_{4}}{(1+\beta )\eta ^{2}-\eta -(\delta +N)}, \\ d_{11}&= d_{2}+d_{8},\quad d_{12}=d_{3}+d_{9}, \quad d_{13}=d_{6}-d_{10},\quad d_{14}=t_{4}(t_{5}-t_{6}), \\ t_{4}&= \frac{1}{1+hh_{2}}, \quad t_{5}=(hR_{1}+1)d_{11}-(hh_{3}+1)d_{1}+(hh_{6}+1)d_{12}, \\ t_{6}&= (hh_{4}+1)d_{4}+(hh_{5}+1)d_{5}+(1+hh_{1})d_{7}-(h\eta +1)d_{13}+1, \\ t_{7}&= (hh_{4}+1)d_{4}+(hh_{1}+1)d_{7}-(h\eta +1)d_{13}+1, \\ K_{1}&= h_{2}t_{4}(hh_{5}+1)-h_{5}, \\ X_{1}&= \frac{2\beta \eta }{(1+\beta )\eta ^{2}-\eta -(\delta +N)}, \quad X_{2}=\frac{2\beta h_{5}}{(1+\beta )h_{5}^{2}-h_{5}-(\delta +N)}. \end{aligned}$$