1 Introduction

Dynamic and rapid development in the electronic industry, material engineering, and nanotechnology, as well as progressive miniaturization, are leading to a continuous reduction of the dimensions of used structures. An important requirement for the design and proper operation of devices based on such structures is a knowledge of their physical properties, including the thermal ones. Since heat transport phenomena in such systems appear to be qualitatively different than in their macroscale equivalents, it is necessary to perform measurements directly on these structures, which in turn requires high spatial resolution. A technique characterized by high spatial resolution and high sensitivity is scanning thermal microscopy (SThM). It provides ample opportunities for local thermal property measurements.

While performing SThM measurements in the contact-mode, several issues must be taken into account. It is commonly mentioned [1, 2] that there exist multiple heat transfer mechanisms through probe–sample thermal contact, e.g., through an air gap, a water meniscus and directly through a solid–solid interface. They all may lead to difficulties in quantitative interpretation of experimental results. Another major issue is the influence of the topography of the sample surface and the quality of the probe–sample contact. Possible solutions of these problems were proposed in Refs. [3–5]. In this paper, a different approach to the quantitative measurements using nanofabricated thermal probes (NThP) is proposed. It is based on determination of the probe resistance changes when the probe is in contact with the sample or in air, far from the sample surface, while maintaining the probe current constant. A simplified theoretical description of the investigated phenomena is discussed in the next section. The experimental setup and procedure as well as reference samples used in the experiment are described in Sect. 3. The results of measurements are presented in Sect. 4. Section 5 contains a comparison between experimental results and predictions of an electro-thermal finite element model of the probe–sample system built in COMSOL MultiPhysics and the analysis in terms of the theoretical model. Final discussion and conclusions close the paper.

2 Theoretical Model

A simplified, quantitative analysis is proposed to describe phenomena associated with heat transfer in the probe–sample system. The generalized equation for equilibrium of the power dissipated in the probe and the heat loses due to convection, according to Newton’s law, and by heat conduction is

$$\begin{aligned} P=h\Delta T+\frac{1}{R_\mathrm{Th}}{\Delta }T, \end{aligned}$$
(1)

where \(h\) is the effective heat transfer coefficient, \({\Delta }T\) indicates the difference between the probe temperature and ambient temperature, and \(R_\mathrm{Th}\) is the thermal resistance for heat flux from the heated region of the probe to the sample. The second component of Eq. 1 is related to heat transfer through the probe–sample thermal contact area, whereas the first component is related to convection cooling of the probe. The electric current flowing through the resistive stripe causes Joule heating, which is most effective at the very tip of the probe. The power losses in the stripe can be expressed as

$$\begin{aligned} P=I_\mathrm{p}^2 \left( {R_0 +{\Delta }R} \right) , \end{aligned}$$
(2)

where \(I_\mathrm{p}\) is the probe current, \(R_{0}\) is the probe resistance at ambient temperature, and \({\Delta }R\) is the probe resistance increase due to probe heating. Assuming a linear dependence,

$$\begin{aligned} {\Delta }R=\beta {\Delta }T, \end{aligned}$$
(3)

where \(\beta \) indicates the temperature coefficient of the resistance. Combining all the above equations leads to the expression,

$$\begin{aligned} {\Delta }R=\frac{R_0}{\frac{1}{\beta I_\mathrm{p}^2}\left( {h+\frac{1}{R_\mathrm{Th}}} \right) -1}. \end{aligned}$$
(4)

The thermal resistance \(R_\mathrm{Th}\) can be expressed as [2, 6–8]

$$\begin{aligned} R_{\mathrm{Th}} =\frac{1}{4\kappa r_\mathrm{Th}}+R_\mathrm{Thp}, \end{aligned}$$
(5)

where the first component describes the so-called constriction resistance, in which \(r_\mathrm{Th}\) is the thermal contact radius and \(\kappa \) is the thermal conductivity of the sample. The second component, \(R_\mathrm{Thp}\), can be understood as the probe resistance to heat transfer from the heated volume to the probe–sample contact area. Considering that the probe is in thermal contact with the sample of very low thermal conductivity or in air, Eq. 5 can be rewritten as

$$\begin{aligned} R_\mathrm{Th}^{\prime } \approx \frac{1}{4\kappa r_\mathrm{Th}} \end{aligned}$$
(6)

as the thermal resistance of the probe \(R_\mathrm{Thp}\) can be neglected in this case. The opposite situation takes place for samples which are good thermal conductors. In this case, the thermal resistance, \(R_\mathrm{Thp}\), constricts the heat flow through the contact. In the experiment, the probe resistances in air and for the probe touching the sample were measured. Their difference can be written in the form,

$$\begin{aligned} {\Delta }R_{\mathrm{a-s}} ={\Delta }R^{\prime }-{\Delta }R={\varGamma }\frac{\zeta -\frac{1}{\kappa _\mathrm{s}}}{\gamma +\frac{1}{\kappa _\mathrm{s}}}, \end{aligned}$$
(7)

where \(\Delta R^{\prime }\) is \(\Delta R\) for \(R_\mathrm{Th}^{\prime }\), and \(\varGamma , \zeta , \gamma \) are functions of \(I_\mathrm{p}, h, \beta , R_\mathrm{Thp}\), and the air thermal conductivity, \(\kappa _\mathrm{a}\). \(\Delta R^{\prime }\) is treated as a reference for the signal registered in contact with the sample. Such an approach makes the measurement less sensitive to instabilities of ambient conditions.

3 Experiment

3.1 NThP Probes

In the experiment, the nanofabricated KNT-SThM-1an thermal probes from Kelvin Nanotechnology were used. The probe consists of a silicon base and \(\mathrm{Si}_{3}\mathrm{N}_{4}\) cantilever on which a NiCr/Pd resistive strip and NiCr/Au contacts are deposited. The probe resistance is in the range of \(250\,\Omega \) to \(400\,\Omega \), and the temperature resistivity coefficient reported by the manufacturer is \(1\,\Omega \,{\cdot } \,\text{ K }^{-1}\). The cantilever is 400 nm thick, and the fine tip radius is estimated to be less than 100 nm. The maximum recommended probe current is 2.0 mA.

3.2 Samples

All samples used in the experiment were reference materials with well-defined thermal properties: BK7 glass, YAG crystal, titanium, iron, nickel, silicon, GaN, copper, and SiC. Their thermal conductivity values are presented in Table 1.

Table 1 Samples used in the experiment and their thermal conductivity values
Full size table

3.3 Experimental Setup

A schematic of the experimental setup is presented in Fig. 1. In the experiment, the probe was connected in series with a 4 k\(\Omega \) balance resistor. This voltage divider was driven by a DC voltage from an internal voltage source of an SR 830 lock-in amplifier (Stanford Research Systems). During the whole experiment, the probe current remained constant at a value of 1.8 mA. The voltage drop on the probe was registered using a 34401A digital multimeter (Agilent Technologies), from which the probe resistance was determined.

Fig. 1
figure 1

Schmatic diagram of experimental setup. The probe is connected in series with the 4 k\(\Omega \) resistor and driven by a DC voltage from the lock-in amplifier. Probe voltage drop is registered by the digital multimeter

Full size image

4 Experimental Results

First, the probe resistance was registered while detaching and approaching the sample. Registration began from a position, when the probe touches the sample, up to the distance where the probe resistance did not depend on the probe–sample distance. Then the signal was registered while approaching back to the sample surface. The control system of the microscope allowed carrying out measurements with a minimum step of \(0.1\,\upmu \)m. Figure 2 presents the detaching-approaching signal dependence registered as a function of the probe mount position \(Z_\mathrm{p}\), illustrating the known hysteresis phenomenon due to Van der Waals forces between the tip and surface. The \(Z_\mathrm{p}\) position was calculated from a readout of the Z-stage position and piezoelectric Z-scanner displacement (this is why the \(Z_\mathrm{p}\) step is not equal to \(0.1\,\upmu \)m). It should be noted that this position cannot be identified with the actual position of the probe tip because of cantilever bending caused by a sample–tip interaction. \(Z_\mathrm{p} = 0\) refers to the probe pressing the sample with a nominal force of 2.0 nN. The constant signal level regime occurs at the beginning of the detaching curve. In this regime, although the \(Z_\mathrm{p}\) value increases, the probe maintains contact with the sample, due to cantilever bending. In the vicinity of \(Z_\mathrm{p} = 0.1\,\upmu \)m, the tip jumps out of contact, which leads to sudden increase in resistance, which is continued until a constant signal level in air is reached. In the approaching curve, the tip falls back in contact at \(Z_\mathrm{p}< 0.1\,\upmu \)m. As a result, hysteresis for \(R\) versus \(Z_\mathrm{p}\) dependence near \(Z_\mathrm{p} = 0.1\,\upmu \)m is observed.

Fig. 2
figure 2

Detaching \((\bullet )\) and approaching \((\circ )\) probe resistance signal dependence registered as a function of Z-scanner indication \(Z_\mathrm{p}\) (logarithmic scale)

Full size image

In a standard measurement, the differences \(\Delta R_\mathrm{a-s}\) between probe resistance values in air and for the probe in contact with the sample were determined for each sample. The probe resistance was registered at three different points on the sample surface and 2 mm above the sample. The average values of \(\Delta R_\mathrm{a-s}\) versus the sample thermal conductivity \(\kappa _\mathrm{s}\) are presented in Fig. 3. During the experiment, \({\Delta }R^{\prime }\), which is the probe resistance increase in air, was not stable, which might be caused by ambient temperature changes. \({\Delta }R^{\prime }\) was therefore registered before and after each \(\Delta R\) measurement. Then two measured values of \({\Delta }R^{\prime }\) were averaged, and this average value was used for calculation of \(\Delta R_\mathrm{a-s}\). It allows obtaining a smooth \(\Delta R_\mathrm{a-s}(\kappa _\mathrm{s})\) curve, while a rough \(\Delta R\) on \(\kappa _\mathrm{s}\) dependence (not shown in the paper) was very noisy. It proves that using the signal measured in air as a reference effectively reduces the influence of environmental conditions on the measurement.

Fig. 3
figure 3

Average values of relative probe resistance changes \(\Delta R_\mathrm{a-s}\) versus sample thermal conductivity \(\kappa _\mathrm{s} (\bullet )\) with fitted theoretical curve (–)

Full size image

Uncertainties were evaluated based on the repeatability of each measurement series and did not exceed 1 %, although they were omitted on the graph. It can be seen that the \(\Delta R_\mathrm{a-s}\) dependence on \(\kappa _{s}\) properly reflects thermal properties—higher \(\Delta R_\mathrm{a-s}\) values designate materials with higher thermal conductivity. The highest one, \(\Delta R_\mathrm{a-s}= 2.52\,\Omega \) was collected for SiC and the lowest one, \(\Delta R_\mathrm{a-s}=1.32\,\Omega \) for BK7. A better differentiation occurs for materials with thermal conductivity values located in the middle of the considered range. A more detailed analysis of the sensitivity dependence on the thermal conductivity is done in the next section.

5 Analysis and Discussion

The theoretical curve described by Eq. 7 was fitted to the experimental data (Fig. 3, solid line). Good agreement between the experimental data and the theoretical model was attained. The correlation coefficient is 0.95. The highest thermal conductivity of a sample used in experiments was 490 \(\text{ W }\,{\cdot }\,\text{ m }^{-1}\,{\cdot }\,\text{ K }^{-1}\). To examine the correctness of the theoretical model also for materials with very high thermal conductivity, numerical simulations were carried out. These results should also allow verification of information about the basic properties of NThP probes, especially the thermal conductivity of the cantilever material. The electro-thermal finite element model of the probe–sample system was created in COMSOL MultiPhysics. The geometry of the model is shown schematically in Fig. 4. The dimensions of individual components reproduce the actual probe geometry. The probe was represented by a 400 nm thick substrate with 140 nm thick contact pads and a 40 nm thick resistive strip. The tip radius has a dimension of about 100 nm, as the contact radius estimated for the real probe. The sample is modeled by a hemisphere, and the probe–sample contact area is surrounded by air. Because of the symmetry of the system, only half of the probe and the sample were considered. Standard boundary conditions were set into the model. This model is similar to the one described in Ref. [9] except for the fact that the air cylinder surrounding the probe and being in contact with the sample was added (this cylinder is not colored in Fig. 4 for clarity). The temperature and heat flux continuity were assumed at all inner boundaries. The symmetry plane was thermally insulated. Outer surfaces are at ambient temperature. It gives the possibility for determination of the voltage drop on the probe heated by a constant current as a function of the parameters of the model (thermal conductivities and heat capacities of the sample and the probe substrate, the electric current through the probe, etc.). It means that analysis of the influence of these parameters on the measured signal is possible. Knowing the voltage drop on the probe and the probe current, the probe resistance can be calculated. The experiment described in the previous section was simulated numerically. In the simulation, the probe voltage signal was calculated for the probe being in thermal contact with materials of different thermal conductivities and in air. Simulation was carried out for values of the sample thermal conductivity coefficient ranging from \(0.2\,\text{ W }\,{\cdot }\,\text{ m }^{-1}\,{\cdot }\,\text{ K }^{-1}\) to \(10\,000\,\text{ W }\,{\cdot }\,\text{ m }^{-1}\,{\cdot }\,\text{ K }^{-1}\). On this basis, the \(\Delta R_\mathrm{a-s}\) values were calculated. It allowed construction of the dependence analogous to the one shown in Fig. 3. The \(\Delta R_\mathrm{a-s}(\kappa _\mathrm{s})\) curves calculated for \(I_\mathrm{p} = 2\,\text{ mA }\) are shown in Fig. 5. Simulations were carried out for three different values of the thermal conductivity of the cantilever material: \(\kappa _\mathrm{cant} = (30, 200,\,\text{ and }\,300)\,\text{ W }\,{\cdot }\,\text{ m }^{-1}\,{\cdot }\,\text{ K }^{-1}\).

Fig. 4
figure 4

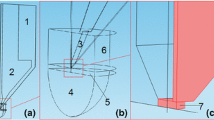
Overall geometry of probe–sample model and zoomed area of probe–sample contact with marked individual elements of the probe: cantilever (a) with resistive strips (b) and contacts (c), being in contact with the hemisphere sample (d). Whole probe is surrounded by air (half-cylinder marked by black lines)

Full size image
Fig. 5
figure 5

Relative probe resistance values \(\Delta R_\mathrm{a-s}\) as a function of thermal conductivity of sample obtained by simulation carried out for different values of thermal conductivity of probe substrate \(-30\,\text{ W }\,{\cdot }\,\text{ m }^{-1}\,{\cdot }\,\text{ K }^{-1}\,(\blacksquare ), 200\,\text{ W }\,{\cdot }\,\text{ m }^{-1}\,{\cdot }\,\text{ K }^{-1}\,(\circ )\), and \(300\,\text{ W }\,{\cdot }\,\text{ m }^{-1}\,{\cdot }\,\text{ K }^{-1}\,(\bullet )\), fitted theoretical curves (–)

Full size image

It can be seen in Fig. 5 that all calculated dependences tend to constant values in the limits of very low and very high values of thermal conductivities. The difference \(\Delta R_\mathrm{a-s}\) is the highest for samples with a high thermal conductivity, and its absolute value grows with a decrease of the thermal conductivity of the cantilever. The slope of \(\Delta R_\mathrm{a-s} (\kappa _{s})\) is the steepest in the central part of the analyzed \(\kappa _{s}\) range. The position of the slope shifts toward lower values of \(\kappa _{s}\) with a decreasing thermal conductivity of the cantilever. Comparing experimental data shown in Fig. 3 with results of numerical analysis, the conclusion can be drawn that the thermal conductivity of the cantilever of the probe used in the experiments is close to \(30\,\text{ W }\,{\cdot }\,\text{ m }^{-1}\,{\cdot }\,\text{ K }^{-1}\).

Each numerical calculated data series was fitted with a theoretical curve. The correlation coefficient reaches 0.99 for all dependences. The theoretical curve parameters \(\varGamma , \zeta , \gamma \), as were mentioned in Sect. 2, are functions of \(R_\mathrm{Thp}\), which in turn depends on the probe substrate thermal properties. For example, the \(\gamma \) parameter is a linear function of \(R_\mathrm{Thp}\). With increasing \(\kappa _\mathrm{cant}, R_\mathrm{Thp}\) decreases, and it should lead to decreases in the \(\gamma \) parameter. This expected trend is confirmed by the analysis.

6 Conclusion

Research described in this paper concerns the possibility for thermal conductivity determination from the relative change of the probe resistance registered by the use of NThP. The presented method can be used for estimation of unknown \(\kappa \) values, based on calibration measurements carried out for reference samples. The difference between the signal measured far from the sample and the one obtained for the probe in thermal contact with the sample can be related to the thermal conductivity of the sample. The relation was derived theoretically and then confirmed by both experimental and numerical results. The theoretical function \(\Delta R_\mathrm{a-s} (\kappa _\mathrm{s})\) was derived based on the simplified analysis; however, it seems to properly describe phenomena occurring in the probe–sample system. The numerical model of the measurement developed by the finite element method well describes real experiments. It can be very useful for further interpretation of experimental data or theoretical model verification, particularly in the \(\kappa _\mathrm{s}\) range which cannot be covered by experimental samples. For further analysis of the correctness of the proposed theoretical model, the influence of different parameters (for example, \(I_\mathrm{p}, h, \beta , R_\mathrm{Thp}\)) will be studied.