A STUDY OF SEMIOTIC REGISTERS IN THE DEVELOPMENT OF THE DEFINITE INTEGRAL OF FUNCTIONS OF TWO AND THREE VARIABLES

ABSTRACT

Tracing the path from a numerical Riemann sum approximating the area under a curve to a definite integral representing the precise area in various texts and online presentations, we found 3 semiotic registers that are used: the geometric register, the numerical register, and the symbolic register. The symbolic register had 3 representations: an expanded sum, a sum in sigma notation, and the definite integral. Reviewing the same texts, we found that in the presentation of double and triple integrals, not a single textbook continues to present the numerical register and the expanded sum representation of the symbolic register. They are implied and the expectation appears to be that students no longer need them. The omission of these representations is quite ubiquitous and correspondingly affects millions of students. Materials that present the missing numerical register representation and the expanded sum representation of the symbolic register throughout topics associated with double and triple integrals have been created. This paper presents the results of a clinical study on the improvement of student comprehension of multivariable integral topics when these representations are included.

Appendices

Appendix 1: A Sample Activity of the Experimental Group

Sample Activity with Solution

Follow the following steps to find the volume below the surface z = f(x,y) = 0.5x ² + y ² + 4 and above the region 0ax ≤ 4, 0 ≤ y ≤ 4 in the xy-plane.

• (a) Draw the region on the xy plane and use a computer, calculator, or physical manipulative to visualize the surface over the region.

  

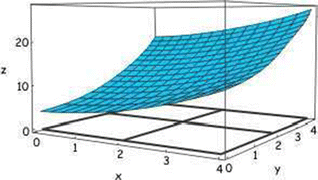
• (b) If there are two divisions in x and two divisions in y and the volume is to be approximated using the middle value for x and y in each division, find x ₁, x ₂, y ₁, y ₂, Δx, and Δy

  $$ {x}_1=1,\kern0.5em {x}_2=3,\kern0.5em {y}_1=1,\kern0.5em {y}_2=3,\kern0.5em \varDelta x=2,\kern0.5em \mathrm{and}\kern0.5em \varDelta y=2 $$

• (c) For each of the four divisions, indicate the point and associated height that will be used to approximate the volume for that division and identify the four cubes with which we will approximate the volume. Note: When possible, both a 2D and a 3D representation in the geometric register are encouraged.

  

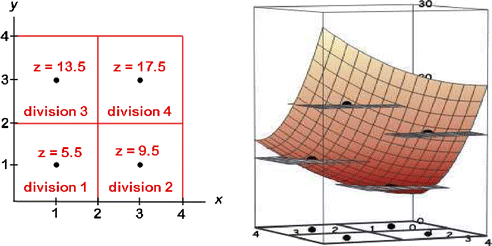
• (d) Use the values obtained in part c to fill in the following table with numerical values. Note: The use of the numerical register is introduced here and finalized in 2f.

  Division	Length	Width	Height	Volume
  1	2	2	5.5	2 × 2 × 5.5
  2	2	2	9.5	2 × 2 × 9.5
  3	2	2	13.5	2 × 2 × 13.5
  4	2	2	17.5	2 × 2 × 17.5

• (e) Fill in the same table below using x ₁, x ₂, y ₁, Δx, and Δy instead of numerical values. The divisions should not change between this and the previous table. Note: The extended sum representation of the symbolic register is introduced here and finalized in 2g

  Division	Length	Width	Height	Volume
  1	Δy	Δx	0.5x 1 2 + y 1 2 + 4	(0.5x 1 2 + y 1 2 + 4)ΔxΔy
  2	Δy	Δx	0.5x 2 2 + y 1 2 + 4	(0.5x 2 2 + y 1 2 + 4)ΔxΔy
  3	Δy	Δx	0.5x 1 2 + y 2 2 + 4	(0.5x 1 2 + y 2 2 + 4)ΔxΔy
  4	Δy	Δx	0.5x 2 2 + y 2 2 + 4	(0.5x 2 2 + y 2 2 + 4)ΔxΔy

• (f) Express the approximate volume numerically. Note: This is a treatment in the numeric register.

  $$ \mathrm{Volume}\approx \left(2\kern0.5em \times \kern0.5em 2\kern0.5em \times \kern0.5em 5.5\right)\kern0.5em +\kern0.5em \left(2\kern0.5em \times \kern0.5em 2\kern0.5em \times \kern0.5em 9.5\right)\kern0.5em +\kern0.5em \left(2\kern0.5em \times \kern0.5em 2\kern0.5em \times \kern0.5em 13.5\right)\kern0.5em +\kern0.5em \left(2\kern0.5em \times \kern0.5em 2\kern0.5em \times \kern0.5em 17.5\right)\kern0.5em =\kern0.5em 184 $$

• (g) Express the same volume obtained in part f using x ₁, x ₂, y ₁, y ₂ Δx, and Δy. Note: This is the expanded sum representation of the symbolic register.

  $$ \left(0.5{x}_1^2\kern0.5em +\kern0.5em {y}_1^2\kern0.5em +\kern0.5em 4\right)\varDelta x\varDelta y\kern0.5em +\kern0.5em \left(0.5{x}_1^2\kern0.5em +\kern0.5em {y}_2^2\kern0.5em +\kern0.5em 4\right)\varDelta x\varDelta y\kern0.5em +\kern0.5em \left(0.5{x}_2^2\kern0.5em +\kern0.5em {y}_1^2\kern0.5em +\kern0.5em 4\right)\varDelta x\varDelta y\kern0.5em +\kern0.5em \left(0.5{x}_2^2\kern0.5em +\kern0.5em {y}_2^2\kern0.5em +\kern0.5em 4\right)\varDelta x\varDelta y $$

• (h) Express the volume obtained in part g in the form ∑ ∑ (o)ΔxΔy. Note: The sum with sigma representation of the symbolic register is introduced here.

  $$ \begin{array}{l}\left[\left(0.5{x}_1^2+{y}_1^2+4\right)\varDelta x\varDelta y+\left(0.5{x}_1^2+{y}_2^2+4\right)\varDelta x\varDelta y\right]+\left[\left(0.5{x}_2^2+{y}_1^2+4\right)\varDelta x\varDelta y+\left(0.5{x}_2^2+{y}_2^2+4\right)\varDelta x\varDelta y\right]\hfill \\ {}={\displaystyle {\sum}_{j=1}^2\left(0.5{x}_1^2+{y}_j^2+4\right)}\;\varDelta y\varDelta x+{\displaystyle {\sum}_{j=1}^2\left(0.5{x}_2^2+{y}_j^2+4\right)}\;\varDelta y\varDelta x\hfill \\ {}={\displaystyle {\sum}_{i=1}^2{\displaystyle {\sum}_{j=1}^2\left(0.5{x}_i^2+{y}_j^2+4\right)\;}}\varDelta y\varDelta x\hfill \end{array} $$

• (i) Using part h as a base, find an expression for the volume if there are n divisions in x and m divisions in y.

  $$ \mathrm{Volume}\approx {\displaystyle \sum_{i=1}^n{\displaystyle \sum_{j=1}^m\left(0.5{x}_i^2+{y}_j^2+4\right)\;\varDelta y\varDelta x}} $$

• (j) Use the fundamental theorem and limits to convert the approximation in part i to a precise value. Note: The definite integral representation of the symbolic register is introduced here.

  $$ \mathrm{Volume}\kern0.5em =\kern0.5em \underset{\begin{array}{c}\hfill n\to \infty \hfill \\ {}\hfill m\to \infty \hfill \end{array}}{ \lim }{\displaystyle \sum}_{i\kern0.5em =\kern0.5em 1}^n{\displaystyle \sum}_{j\kern0.5em =\kern0.5em 1}^m\kern1em \left(0.5{x}_i^2\kern0.5em +\kern0.5em {y}_j^2\kern0.5em +\kern0.5em 4\right)\varDelta y\varDelta x\kern0.5em =\kern0.5em \underset{0}{\overset{4}{{\displaystyle \int }}}\underset{0}{\overset{4}{{\displaystyle \int }}}\left(0.5{x}^2\kern0.5em +\kern0.5em {y}^2+\kern0.5em 4\right)\operatorname{d}y\operatorname{d}x $$

End Activity

Some of these activities also include density functions which introduce the verbal register. For example, with cubic coordinates, the units of x, y, and z are meters; there is a density function f with units of $\frac{\mathrm{fish}}{m^3}$; and students are expected to find the number of fish in a cubic tank.

Appendix 2: Specific Interview Questions

The following questions were presented to six students in the control group and five students in the experimental group. In the results section of the questions, the final course grade for each student associated with a result is presented in parentheses.

Question 1: Conversion from geometric register to symbolic register

x = meters

y = meters

z = f(x,y) = height over a point (x,y) in meters.

What is an expression for the volume under the surface f and above the shaded region? (Students were physically shown a surface over the region).

All efforts were made in question 1 to assure that students visualized the solid associated with the geometric register. The results are presented in Table 7.

Table 7 The results of interview question 1

Question 2: Conversions from symbolic register to geometric and verbal registers

x = meters

y = meters

$$ f\left(x,y\right)=\mathrm{density}=\frac{\mathrm{kg}}{{\mathrm{m}}^2} $$

Given $\underset{1}{\overset{9}{{\displaystyle \int }}}\underset{2}{\overset{6}{{\displaystyle \int }}}\operatorname{d}y\operatorname{d}x$

• A. What are the units of this integral?

• B. Is it possible to find a result for the integral without evaluating it?

It should be noted that students could interpret the integral as an area or they could recognize that $\underset{1}{\overset{9}{{\displaystyle \int }}}\underset{2}{\overset{6}{{\displaystyle \int }}}\operatorname{d}y\operatorname{d}x\kern0.5em =\kern0.5em \underset{1}{\overset{9}{{\displaystyle \int }}}\underset{2}{\overset{6}{{\displaystyle \int }}}(1)\operatorname{d}y\operatorname{d}x$ and interpret the integral as the volume under the surface z = 1 over the indicated region. The goal was to see if students would recognize that f was not a part of this problem. The results are presented in Table 8.

Table 8 The results of interview question 2

Question 3:

The height of a surface at a given point (x,y) is given by the formula f(x,y) = x + y + 1, and we wish to find the volume below this surface and over the region shown below.

It should be noted that the students had a large sheet of paper with a very large representation of the region and they were physically shown the plane z = x + y + 1 over this region to assure that the geometric register was involved.

• A. We wish to approximate the volume using two divisions in x and two divisions in y, can you draw the associated divisions and indicate the length, width, and height of each division if we use the smallest height in each region?

  

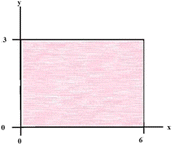
• B. Now we wish to approximate the same volume using three divisions in x and three divisions in y, can you draw the associated divisions and indicate the length, width, and height of each division if we use the smallest height in each region?

  

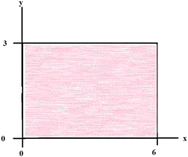
  Questions 3A and 3B were to establish the ability to convert from the geometric register to the numerical register.

• C. Between A and B, which approximation is better?

• D. Is there something we can we do to make these approximations even more precise?

  Questions 3C and 3D were to determine whether students understand the underlying limits that are used to transition from the sum with sigma representation of the symbolic register to the definite integral representation of the symbolic register.

• E. We are going to go back to your approximation in A. Can this approximation be expressed using sigma notation? If so, how? If not, why not?

  Question 3E was to determine whether students could do the conversion from the numerical register to the symbolic register (sum with sigma representation). Any double sigma expression that could represent the numerical approximation was considered a success.

• F. Based on the answer to E

  • (a) If they have the sigma,

    • 1. How does this sum in sigma form change if we use the approximation in B instead of the approximation in A?

    • 2. How can we make the approximation more and more precise in sigma form?

    • 3. How do we obtain the precise value for the volume from this sigma form?

  • (b) If they do not have the sigma

    • 1. If we had been able to put this in sigma notation, would there be any advantage?

    • 2. If no, leave the topic

    • 3. If yes, what would the advantage be? How would we make the expression more precise in sigma form?

    • 4. How do we obtain the precise value of the volume from the sigma form?

The purpose of question 3F was to determine whether the concept which was established in 3C and 3D (that more divisions make the approximation more precise) could be used to do the treatment relating the sum with sigma representation to the definite integral representation in the symbolic register. Any scheme taking the limit of a double sigma to arrive at a double integral was considered a success. The results of question 3 are presented in Table 9.

Table 9 The results of interview question 3

Question 4: Verbal register to numerical register and verbal register to integral representation of the symbolic register

In the region below x = km, y = km and the density of people is defined by f(y) = 9 − y ² persons/km². We are interested in the number of people that live in the region. In the interview, students were provided an explanation that perhaps there is a river that runs where y < 0 and as people prefer to live near the river, the density of people in this region is greater the closer we are to the river.

• A. How would you approximate the number of people that live in this region?

  Any Riemann sum was considered a success for this part A of the question.

• B. If student performs divisions in both x and y: Do we have to divide in both x and y?

  Some prompting was provided for part B but only a Riemann sum with divisions in y and not in x was considered a success. If they provided such a Riemann sum in part A, then part B was automatically considered a success.

• C. Can you provide an expression for the precise number of people?

  Any correct integral expression was considered a success for part C of the question.

• D. If they provide a double integral in part C, ask if the precise number of people can be expressed as a single integral.

  As with part B, some prompting was provided for part D but only a single integral expression in terms of y was considered a success. If they provided the correct single integral in part C, it was automatically considered a success in part D. The results are presented in Table 10.

  Table 10 The results of interview question 4