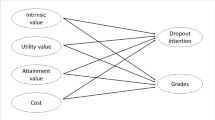
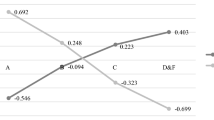
Abstract
A number of studies have concluded that when students have greater confidence about their math skills and are aware of its usefulness, they have a more positive perception of the subject. This article aims to examine whether this pseudo linear trend in the relationship between affective and instrumental dimensions is also true of the university context. Special attention is devoted to the articulation of these dimensions in structuring student perceptions of quantitative methods so as to identify the various forms that this interaction can assume. Our second aim is to understand how the perceptions of these subjects are constructed by students from degree courses in distinct scientific areas. Can we speak of group dynamics whereby socialization within each degree course triggers the sharing of similar perceptions? We concluded that a certain linear trend can also be identified in the university context in the relationship between the affective dimension and usefulness of quantitative methods i.e., that the highest levels in the perception of the usefulness of these subjects corresponded to the highest levels of self confidence and enjoyment of the subjects. However, in addition to this scenario there is another configuration in which negative feelings coexist with the recognition of the usefulness of quantitative methods subjects. Namely, lower levels of self confidence and enjoyment of these subjects can also be associated with high levels of perceived usefulness. We also concluded that there is evidence of what we designated a certain course culture in the perceptions about quantitative methods. Nevertheless, when our observation is extended to the scientific area the heterogeneity of the perceptions becomes evident. Another important finding is the rejection of the thesis, at least in the university context, that defends the lack of self-confidence in quantitative methods among females student.







Similar content being viewed by others
Notes
These are the courses with fewest quantitative methods subjects (only two when the questionnaire was applied).
References
Ainley, M. (2006). Connecting with learning: Motivation, affect and cognition in interest processes. Educational Psychology Review, 18, 391–405.
Borasi, R. (1990). The invisible hand operating in mathematics instruction: Students’ conceptions and expectations. In T. J. Cooney & C. Hirsh (Eds.), Teaching and learning mathematics in the 1990s. Reston: NCTM.
Carvalho, H. (2008). Análise de Multivariada de Dados Qualitativos, Utilização da Análise de Correspondências Múltiplas com o SPSS. Lisboa: Sílabo.
de Geer, V. (1993a). Multivariate analysis of categorical data: Theory. London: Sage Publications.
de Geer, V. (1993b). Multivariate analysis of categorical data: Applications. London: Sage Publications.
Fennema, E. (2000). Gender and mathematics: What is known and what do I wish was known? In Fifth Annual forum of the national institute for science education. Detroit.
Fennema, E., & Sherman, J. (1977). Sex-related differences in mathematics achievement and spatial visualization and affective factors. American Educational Research Journal, 14(1), 51–71.
Fennema, E., & Sherman, J. (1978). Sex-related differences in mathematics achievement and related factors: a further study. Journal for Research in Mathematics Education, 9(3), 189–203.
Gifi, A. (1996). Nonlinear multivariate analysis. New York: Wiley.
Grootenboer, P., & Hemmings, B. (2007). Mathematics performance and the role played by affective and background factors. Mathematics Education Research Journal, 19(3), 3–20.
Heiser, W., & Meulman, J. (1994). Homogeneity analysis: Exploring the distribution of variables and their nonlinear relationships. In M. Greenacre & J. Blasius (Eds.), Correspondence analysis in the social sciences (pp. 179–209). London: Academic Press.
Kilpatrick, J., & Silver, E. (2000). Unfinished business: Challenges for mathematics educators in the next decades. Yearbook (pp. 223–235).
Kloosterman, P., Raymond, A., & Emenaker, C. (1996). Students’ beliefs about mathematics: A three-year study. The Elementary School Journal, 97(1), 39–56.
Kloosterman, P., & Stage, F. (1992). Measuring beliefs about mathematical problem solving. School Science and Mathematics, 92(3), 109–115.
Lawless, K. A., & Kulikowich, J. M. (2006). Domain knowledge and individual interest: The effects of academic level and specialization in statistics and psychology. Contemporary Educational Psychology, 31(1), 30–43.
Meulman, J. (1992). The integration of multidimensional scaling and multivariate analysis with optimal transformations. Psychometrika, 57(4), 539–565.
Muis, K. (2004). Personal epistemology and mathematics: A critical review and synthesis of research. Review of Educational Research, 74(3), 317–377.
Onwuegbuzie, A., & Wilson, V. (2003). Statistics anxiety: Nature, etiology, antecedents, effects, and treatments—A comprehensive review of the literature. Teaching in Higher Education, 8(2), 195–209.
Ramalho, G. (1994). As Nossas Crianças e a Matemática. Caracterização da Participação dos Alunos Portugueses no Second International Assessment of Educational Progress. Lisboa: DEPGEF.
Ramos, M., & Carvalho, H. (2009). Quantitative methods in higher education: A typology of representations. Educação e Pesquisa [online], 35(1), 15–32. Available from: <http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1517-97022009000100002&lng=en&nrm=iso>. ISSN 1517-9702. doi: 10.1590/S1517-97022009000100002.
Schoenfeld, A. (1988). When good teaching leads to bad results: The disasters of “well-taught” mathematics courses. Educational Psychologist, 23(2), 145–166.
Schoenfeld, A. (1989). Explorations of students’ mathematical beliefs and behavior. Journal for Research in Mathematics Education, 20(4), 338–355.
SPSS Inc. (2009). SPSS base 15.0 user’s guide. Chicago, USA: Prentice Hall.
Stage, F. K., & Kloosterman, P. (1995). Gender, beliefs and achievement in remedial college-level mathematics. Journal of Higher Education, 66(3), 294–311.
Walker, W., & Plata, M. (2000). Race/gender/age differences in college mathematics students. Journal of Developmental Education, 23(3), 24–32.
Author information
Authors and Affiliations
Corresponding author
Appendices
Rights and permissions
About this article
Cite this article
Ramos, M., Carvalho, H. Perceptions of quantitative methods in higher education: mapping student profiles. High Educ 61, 629–647 (2011). https://doi.org/10.1007/s10734-010-9353-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10734-010-9353-3