An optimization model to determine appointment scheduling window for an outpatient clinic with patient no-shows

Abstract

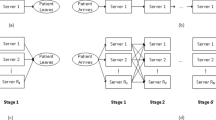
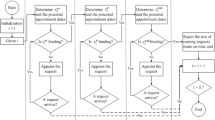
This paper investigates appointment scheduling for an outpatient department in West China Hospital (WCH), one of the largest single point of access hospitals in the world. Our pilot data analysis shows that the appointment system at WCH can be improved through leveraging the scheduling window (i.e., the number of days in advance a patient makes an appointment for future services). To gain full insight into this strategy, our study considers two cases, based on if patients are willing to wait for scheduled appointments or not. We developed a stylized single server queueing model to find optimal scheduling windows. Results show that, when patients are less sensitive to time delay (i.e., patients will wait for scheduled services), levering scheduling windows is not effective to minimize the total cost per day of the appointment system. In contrast, when patients are sensitive to time delay (i.e., patients may find services elsewhere), then our model considers the potential cost of physician idle time. The modeling results indicate that the total cost per day is relatively sensitive to the magnitude of scheduling window. Thus, adopting a proper scheduling window is very important. In addition, our study proves that the cost functions of both cases are quasi-concave, which are also validated by actual data drawn from the Healthcare Information System at WCH. A comparison of numerical results between two cases is made to draw further managerial insights into scheduling policies for WCH. Discussion of our findings and research limitations are also provided.

Appendix A: Proofs of the Proposition

Lemma 1^[18]. For a, c, b, d ≥ 0, if $\frac{c}{d}\le \left(<\right)\frac{c}{d},$ then

$$ \frac{c}{d}\le \left(<\right)\frac{a+c}{b+d}\le \left(<\right)\frac{a}{b} $$

Proof of Proposition 1:

First, we prove S₁ is nonempty. ∀ρ, 1 ∈ S₁. Since $T(0)=\theta \lambda, T(1)=\frac{\theta \lambda \rho}{1+\rho }$

$$ \because \frac{\rho }{1+\rho }<1\therefore T(1)<T(0) $$

For N ≥ 2, N ∈ S₁,

$$ {\displaystyle \begin{array}{l}T\left(N-1\right)=\frac{\xi \sum \limits_{j=1}^{N-1}\left(j-1\right){\rho}^j+{\theta \lambda \rho}^{N-1}}{\sum \limits_{j=0}^{N-1}{\rho}^j}\\ {}\kern3.75em \ge \xi \left(N-1\right)+\theta \lambda \\ {}\kern4em =\frac{\xi \left(N-1\right){\rho}^N+{\theta \lambda \rho}^N}{\rho^N}\end{array}} $$

(13)

According to Lemma 1,

$$ {\displaystyle \begin{array}{l}T\left(N-1\right)=\frac{\xi \sum \limits_{j=1}^{N-1}\left(j-1\right){\rho}^j+{\theta \lambda \rho}^{N-1}}{\sum \limits_{j=0}^{N-1}{\rho}^j}\\ {}\kern3.5em \ge \xi \left(N-1\right)+\theta \lambda \\ {}\kern3.75em =\frac{\xi \left(N-1\right){\rho}^N+{\theta \lambda \rho}^N}{\rho^N}\end{array}} $$

(14)

i.e. ∀N ∈ S, T(N) ≤ T(N − 1).

Consider sup S <  ∞ , let ${N}_1^{\ast }={supS}_1,$ we need to prove T(N) is increasing in N, i.e. $T\left({N}_1^{\ast }+1\right)>T\left({N}_1^{\ast}\right)$.

Let’s set

$$ g\left({N}_1^{\ast}\right)=\xi \left({N}_1^{\ast }-1\right)+\theta \lambda, $$

Apparently,

$$ {\displaystyle \begin{array}{l}T\left({N}_1^{\ast}\right)=\frac{\xi \sum \limits_{j=1}^{N_1^{\ast }}\left(j-1\right){\rho}^j+{\theta \lambda \rho}^{N_1^{\ast }}}{\sum \limits_{j=0}^{N_1^{\ast }}{\rho}^j}\\ {}\kern2.75em <\frac{\xi \left({N}_1^{\ast }-1\right)\sum \limits_{j=0}^{N_1^{\ast }}{\rho}^j+\theta \lambda \sum \limits_{j=0}^{N_1^{\ast }}{\rho}^j}{\sum \limits_{j=0}^{N_1^{\ast }}{\rho}^j}\\ {}\kern3em =g\left({N}_1^{\ast}\right)\end{array}} $$

(15)

$$ g\left({N}_1^{\ast}\right)<\xi {N}_1^{\ast }+\theta \lambda =g\left({N}_1^{\ast }+1\right) $$

(16)

According to Lemma 1, Eqs. (15) and (16)

$$ {\displaystyle \begin{array}{l}T\left({N}_1^{\ast}\right)=\frac{\xi \sum \limits_{j=1}^{N_1^{\ast }}\left(j-1\right){\rho}^j+{\theta \lambda \rho}^{N_1^{\ast }}}{\sum \limits_{j=0}^{N_1^{\ast }}{\rho}^j}\\ {}\kern2.5em <\frac{\xi \sum \limits_{j=1}^{N_1^{\ast }}\left(j-1\right){\rho}^j+{\theta \lambda \rho}^{N_1^{\ast }}+\xi {N}_1^{\ast }{\rho}^{N^{\ast }+1}+{\theta \lambda \rho}^{N_1^{\ast }+1}}{\sum \limits_{j=0}^{N_1^{\ast }}{\rho}^j+{\rho}^{N_1^{\ast }+1}}\\ {}\kern2.5em =T\left({N}_1^{\ast }+1\right)\end{array}} $$

(17)

Then, we could obtain that T(N) is increasing in N.

In summary, T(N) is decreasing as N increases to ${N}_1^{\ast }$, and then strictly increasing. The objective function T(N) is quasi-concave in N.

Proof of Proposition 2:

Same as Proposition 1, T^′(1) < T^′(0)

For N ≥ 2, N ∈ S₂

$$ {\displaystyle \begin{array}{l}{T}^{\prime}\left(N-1\right)=\frac{\xi \sum \limits_{i=2}^{N-1}\prod \limits_{j=1}^i\left(i-1\right){\rho}_j^{\prime }+\theta \lambda \prod \limits_{j=1}^{N-1}{\rho}_j^{\prime }+\omega \lambda}{1+\sum \limits_{i=1}^{N-1}\prod \limits_{j=1}^i{\rho}_j^{\prime }}\\ {}\kern3.25em \ge \xi \left(N-1\right)+\theta \lambda -\frac{\theta \lambda}{\rho_N^{\prime }}\\ {}\kern3.25em =\frac{\xi \left(N-1\right)\prod \limits_{j=1}^N{\rho}_j^{\prime }+\theta \lambda \prod \limits_{j=1}^N{\rho}_j^{\prime }-\theta \lambda \prod \limits_{j=1}^{N-1}{\rho}_j^{\prime }}{\prod \limits_{j=1}^N{\rho}_j^{\prime }}\end{array}} $$

(18)

According to Lemma 1 and function (18)

$$ {\displaystyle \begin{array}{l}{T}^{\prime}\left(N-1\right)=\frac{\xi \sum \limits_{i=2}^{N-1}\prod \limits_{j=1}^i\left(i-1\right){\rho}_j^{\prime }+\theta \lambda \prod \limits_{j=1}^{N-1}{\rho}_j^{\prime }+\omega \lambda}{1+\sum \limits_{i=1}^{N-1}\prod \limits_{j=1}^i{\rho}_j^{\prime }}\\ {}\ge \frac{\xi \sum \limits_{i=2}^{N-1}\prod \limits_{j=1}^i\left(i-1\right){\rho}_j^{\prime }+\theta \lambda \prod \limits_{j=1}^{N-1}{\rho}_j^{\prime }+\omega \lambda +\xi \left(N-1\right)\prod \limits_{j=1}^N{\rho}_j^{\prime }+\theta \lambda \prod \limits_{j=1}^N{\rho}_j^{\prime }-\theta \lambda \prod \limits_{j=1}^{N-1}{\rho}_j^{\prime }}{1+\sum \limits_{i=1}^{N-1}\prod \limits_{j=1}^i{\rho}_j^{\prime }+\prod \limits_{j=1}^N{\rho}_j^{\prime }}\\ {}\kern3.5em =\frac{\xi \sum \limits_{i=2}^N\prod \limits_{j=1}^i\left(i-1\right){\rho}_j^{\prime }+\theta \lambda \prod \limits_{j=1}^N{\rho}_j^{\prime }+\omega \lambda}{1+\sum \limits_{i=1}^N\prod \limits_{j=1}^i{\rho}_j^{\prime }}\\ {}\kern3.5em ={T}^{\prime }(N)\end{array}} $$

Also, consider sup S₂ <  ∞ , let ${N}_2^{\ast }={supS}_2,$we need to prove ${T}^{\prime}\left({N}_2^{\ast }+1\right)>{T}^{\prime}\left({N}_2^{\ast}\right)$.

Let’s set

$$ {g}^{\prime}\left({N}_2^{\ast}\right)=\xi \left({N}_2^{\ast }-1\right)+\theta \lambda +\omega \lambda \hbox{-} \frac{\theta \lambda}{\rho_{N_2^{\ast}}^{\prime }}, $$

and ${g}^{\prime}\left({N}_2^{\ast }+1\right)=\xi {N}_2^{\ast }+\theta \lambda +\omega \lambda -\frac{\theta \lambda}{\rho_{N_2^{\ast }+1}^{\prime }}>{g}^{\prime}\left({N}_2^{\ast}\right)$

$$ {\displaystyle \begin{array}{l}{T}^{\prime}\left({N}_2^{\ast}\right)=\frac{\xi \sum \limits_{i=2}^{N_2^{\ast }}\prod \limits_{j=1}^i\left(i-1\right){\rho}_j^{\prime }+\theta \lambda \prod \limits_{j=1}^{N_2^{\ast }}{\rho}_j^{\prime }+\omega \lambda}{1+\sum \limits_{i=1}^{N_2^{\ast }}\prod \limits_{j=1}^i{\rho}_j^{\prime }}\\ {}<\frac{\xi \left[{\rho}_1^{\prime }{\rho}_2^{\prime }+\cdots +\left({N}^{\ast }-1\right){\rho}_1^{\prime }{\rho}_2^{\prime}\cdots {\rho}_{N^{\ast}}^{\prime}\right]+\xi {N}_2^{\ast}\prod \limits_{j=1}^{N_2^{\ast }+1}{\rho}_j^{\prime }+\theta \lambda \prod \limits_{j=1}^{N_2^{\ast }}{\rho}_j^{\prime }+\omega \lambda}{1+\sum \limits_{i=1}^{N_2^{\ast }}\prod \limits_{j=1}^i{\rho}_j^{\prime }+\prod \limits_{j=1}^{N_2^{\ast }+1}{\rho}_j^{\prime }}\\ {}\kern2.75em =\frac{\xi \sum \limits_{i=2}^{N_2^{\ast }+1}\prod \limits_{j=1}^i\left(i-1\right){\rho}_j^{\prime }+\theta \lambda \prod \limits_{j=1}^{N_2^{\ast }+1}{\rho}_j^{\prime }+\omega \lambda}{1+\sum \limits_{i=1}^{N^{\ast }+1}\prod \limits_{j=1}^i{\rho}_j^{\prime }}\\ {}\kern2.75em ={T}^{\prime}\left({N}_2^{\ast }+1\right)\end{array}} $$

In summary, T^′(N) is decreasing asNincreases to ${N}_2^{\ast }$, and then strictly increasing. The objective function T^′(N)is quasi-concave in N.