Skip to main content
SpringerLink
Log in

A system model of work flow in the patient room of hospital emergency department

  • Published:
Health Care Management Science Aims and scope Submit manuscript

Abstract

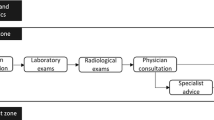
Modeling and analysis of patient flow in hospital emergency department (ED) is of significant importance. In a hospital ED, the patients spend most of their time in the patient room and most of the care delivery services are carried out during this time period. In this paper, we propose a system model to study patient (or work) flow in the patient room of an ED when the resources are partially available. A closed and re-entrant process model is developed to characterize the care service activities in the patient room with limited resources of doctors, nurses, and diagnosis tests. Analytical calculation of patient’s length of stay in the patient room is derived, and monotonic properties with respect to care service parameters are investigated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Bernstein SL, Asplin BR (2006) Emergency department crowding: old problems, new solutions. Emerg Med Clin North Am 24(4):821–837

    Article  Google Scholar 

  2. Jayaprakash N et al (2009) Crowding and delivery of healthcare in emergency departments: the european perspective. West J Emerg Med 10(4):233–239

    Google Scholar 

  3. Sacchetti A et al (2002) Contribution of ED admissions to inpatient hospital revenue. Am J Emerg Med 20(1):30–31

    Article  Google Scholar 

  4. Kennedy J et al (2004) Access to emergency care: restricted by long waiting times and cost and coverage concerns. Ann Emerg Med 43(5):567–573

    Article  Google Scholar 

  5. Hoot NR, Aronsky DA (2008) Systematic review of emergency department crowding: causes, effects and solutions. Ann Emerg Med 52(2):126–136

    Article  Google Scholar 

  6. Brenner S et al (2010) Modeling and analysis of the emergency department at university of kentucky chandler hospital using simulations. J Emerg Nurs 36(3):303–310

    Article  Google Scholar 

  7. Zeng Z et al (2012) A simulation study to improve quality of care in the emergency department of a community hospital. J Emerg Nurs 38(3):322–328

    Article  Google Scholar 

  8. Wang J et al (2012) Reducing length of stay in emergency department: a simulation study at a community hospital. IEEE Trans Syst Man Cybern Syst Hum 42(6):1314–1322

    Article  Google Scholar 

  9. Jacobson SH et al (2006) Discrete-event simulation of health care systems. In: Hall RW (ed) Patient flow: reducing delay in healthcare delivery, vol 91. Springer, International Series in Operations Research & Management Science, pp 211–252

  10. Brailsford SC (2007) Advances and challenges in healthcare simulation modeling: tutorial. In: Proceedings of the 39th winter simulation conference, pp 1436–1448

  11. Wiler JL, Griffey RT, Olsen T (2011) Review of modeling approaches for emergency department patient flow and crowding research. Acad Emerg Med 18(12):1371–1379

    Article  Google Scholar 

  12. Fomundam S, Herrmann J (2007) A survey of queuing theory applications in health care. Technicial report No. 2007–24, the Institute for Systems Research, University of Maryland, College Park

  13. Koizumi N (2002) A queueing network model with blocking: analysis of congested patients flows in mental health systems. PhD dissertation, University of Pensylvania, Philadelphia

  14. Caglar T (2005) A queueing theoretic approach to gridlock prediction in emergency departments. Master Thesis, Virginia Polytechnic Institute and State University, Blacksburg

  15. Au L et al (2009) Predicting overflow in an emergency department. IMA J Manag Math 20(1):39–49

    Article  Google Scholar 

  16. Green LV (2006) Queueing analysis in healthcare. In: Hall RW (ed) Patient flow: reducing delay in healthcare delivery, vol 91. Springer, New York, pp 281–308

    Chapter  Google Scholar 

  17. Green LV et al (2006) Using queueing theory to increase the effectiveness of emergency department provider staffing. Acad Emerg Med 13(1):61–68

    Article  Google Scholar 

  18. Au-Yeung SWM, Harrison PG, Knottenbelt WJ (2007) Approximate queueing network analysis of patient treatment times. In: Proceedings of the 2nd international conference on performance evaluation methodologies and tools. 321 ariticle 45

  19. Mayhew L, Smith D (2008) Using queuing theory to analyse the governments 4-h completion time target in accident and emergency departments. Health Care Manag Sci 11(1):11–21

    Article  Google Scholar 

  20. de Bruin AM et al (2007) Modeling the emergency cardiac in-patient flow: an application of queuing theory. Health Care Manag Sci 10(2):125–137

    Article  Google Scholar 

  21. Saghafian S et al (2012) Complexity-based triage: a tool for improving patient safety and operational efficiency. Ross School of Business Paper No. 1161

  22. Saghafian S et al (2012) Patient streaming as a mechanism for improving responsiveness in emergency departments. Oper Res 60(5):1080–1097

    Article  Google Scholar 

  23. Helm JE, Beygi SA, Van Oyen MP (2012) Design and analysis of hospital admission control for operational effectiveness. Prod Oper Manag 20(3):359–374

    Article  Google Scholar 

  24. Armony M et al (2011) Patient flow in hospitals: a data-based queueing-science perspective. Stoch Syst 6(3)

  25. Li J, Meerkov SM (2009) Production systems engineering. Springer, New York

    Book  Google Scholar 

  26. Liu Y, Li J (2010) Split and merge production systems: performance analysis and structural properties. IIE Trans 42(6):422–434

    Article  Google Scholar 

  27. Biller S et al (2009) Closed Bernoulli production lines: analysis, continuous improvement, and leanness. IEEE Trans Autom Sci Eng 6(1):168–180

    Article  Google Scholar 

  28. Wang C, Li J (2010) Approximate analysis of re-entrant lines with Bernoulli reliability models. IEEE Trans Autom Sci Eng 7(3):708–715

    Article  Google Scholar 

  29. Wang J et al (2012) Modeling and analysis of work flow and staffing level in a computed tomography division of university of wisconsin medical foundation. Health Care Manag Sci 15(2):108–120

    Article  Google Scholar 

  30. Xie X et al (2013) Improving response-time performance in acute care delivery: a systems approach. Conditionally accepted by IEEE Transactions on Automation Science and Engineering

Download references

Author information

Authors and Affiliations

  1. Laureate Education Inc., Baltimore, MD, 21202, USA

    Junwen Wang

  2. Department of Industrial and Systems Engineering, University of Wisconsin, Madison, WI, 53706, USA

    Jingshan Li

  3. Trauma and Emergency Services, University of Kentucky Chandler Medical Center, Lexington, KY, 40506, USA

    Patricia K. Howard

Authors
  1. Junwen Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jingshan Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Patricia K. Howard
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jingshan Li.

Additional information

This paper is supported in part by NSF Grants No. CMMI 1063671 and 1233807.

Appendix: Proofs

Appendix: Proofs

Proof of Proposition 1

By adding the balance equations and eliminating the identical terms, the process throughput TP follows immediately. The patients may leave the system when they are ready for the second service and the provider is available, i.e.,

$$TP=c_{2}[P(1;0,1)+P(1;1,1)].$$

From the Little’s law, the length of stay is obtained through the inverse of TP since only one patient is in the system. □

Proof of Corollary 1

Define the steady state probabilities as follows:

$$ \begin{array}{rll}\pi_{0}=P(0;0,0), & \pi_{1}=P(0;0,1), & \pi_{2}=P(0;1,0), \\\pi_{3}=P(0;1,1), & \pi_{4}=P(1;0,0), & \pi_{5}=P(1;0,1), \\\pi_{6}=P(1;1,0), &\quad \pi_{7}=P(1;1,1).\end{array}$$

By adding Eqs. 1, 2, 3, and 4 with Eqs. 5, 6, 7, and 8, respectively, we obtain

$$ \begin{array}{rll} (\pi_{0}+\pi_{4})(\mu_{1}+\mu_{2})&=&(\pi_{2}+\pi_{6})\lambda_{1}+(\pi_{1}+\pi_{5})\lambda_{2}, \\(\pi_{1}+\pi_{5})(\mu_{1}+\lambda_{2})&=&(\pi_{3}+\pi_{7})\lambda_{1}+(\pi_{0}+\pi_{4})\mu_{2}, \\(\pi_{2}+\pi_{6})(\lambda_{1}+\mu_{2})&=&(\pi_{0}+\pi_{4})\mu_{1}+(\pi_{3}+\pi_{7})\lambda_{2}, \\(\pi_{3}+\pi_{7})(\lambda_{1}+\lambda_{2})&=&(\pi_{1}+\pi_{5})\mu_{1}+(\pi_{2}+\pi_{6})\mu_{2}.\end{array} $$

Then, it follows that

$$ \begin{array} {rll} L_{0}&:=&\pi_{0}+\pi_{4}=\frac{\lambda_{1} \lambda_{2}}{(\lambda_{1}+\mu_{1})(\lambda_{2}+\mu_{2})}, \\[5pt] L_{1}&:=&\pi_{1}+\pi_{5}=\frac{\lambda_{1} \mu_{2}}{(\lambda_{1}+\mu_{1})(\lambda_{2}+\mu_{2})}, \\[5pt] L_{2}&:=&\pi_{2}+\pi_{6}=\frac{\mu_{1} \lambda_{2}}{(\lambda_{1}+\mu_{1})(\lambda_{2}+\mu_{2})}, \\[5pt] L_{3}&:=&\pi_{3}+\pi_{7}=\frac{\mu_{1} \mu_{2}}{(\lambda_{1}+\mu_{1})(\lambda_{2}+\mu_{2})}.\end{array} $$

Replacing with \(\pi _{i},i=0,1,2,3\) to rewrite Eqs. 1–4, we have

$$ \begin{array}{rll}\pi_{0}(\mu_{1}+\mu_{2})&=&\pi_{1} \lambda_{2}+\pi_{2} \lambda_{1}, \\\pi_{1}(\mu_{1}+\lambda_{2}+c_{2})&=&\pi_{0} \mu_{2}+\pi_{3} \lambda_{1}+L_{1} c_{2}, \\\pi_{2}(\lambda_{1}+\mu_{2}+c_{1})&=&\pi_{0} \mu_1+\pi_{3} \lambda_{2}, \\\pi_{3}(\lambda_{1}+\lambda_{2}+c_{1}+c_{2})&=&\pi_{1} \mu_{1}+\pi_{2} \mu_{2}+L_{3}c_{2}.\end{array} $$

Then, it implies that

$$ X_{2}=A_{2}^{-1}B_{2}.$$

where

$$ A_{2} = \left(\begin{array}{llll}\mu_{1}+\mu_{2} & -\lambda_{2} & -\lambda_{1} & 0 \\-\mu_{2} & \mu_{1}+\lambda_{2}+c_{2} & 0 & -\lambda_{1} \\-\mu_{1} & 0 & \lambda_{1}+\mu_{2}+c_{1} & -\lambda_{2} \\0 & -\mu_{1} & -\mu_{2} & \lambda_{1}+\lambda_{2}+c_{1}+c_{2} \\\end{array}\right).$$
$$ \begin{array}{rll} X_{2}&=&[\pi_{0},\pi_{1},\pi_{2},\pi_{3}]^{T}, \\[5pt]B_{2}&=&[0,L_{1}c_{2},0,L_{3}c_{2}]^{T}\\[5pt]&=&\bigg[0,\frac{\lambda_{1}\mu_{2}c_{2}}{(\lambda_{1}+\mu_{1})(\lambda_{2}+\mu_{2})},0, \frac{\mu_{1}\mu_{2}c_{2}}{(\lambda_{1}+\mu_{1})(\lambda_{2}+\mu_{2})}\bigg]^{T}. \end{array} $$

Since now the matrix dimension is small, it is possible to express its inverse in an explicit format. Thus, after some manipulation, we obtain

$$ \begin{array}{rll} \pi_{0}&=&\lambda_{2}c_{2}L_{1}\frac{(c_{1}+\lambda_{1}+\mu_{1})E+F}{c_{1}\mu_{1}E^{2}+(c_{1}+\lambda_{1}+\mu_{1})EF+F^{2}},\\\pi_{1}&=&c_{2}L_{1}\frac{(c_{1}+\lambda_{1}+\mu_{1})\mu_{2}E+c_{1}\mu_{1}E+\mu_{2}F}{c_{1}\mu_{1}E^{2}+(c_{1}+\lambda_{1}+\mu_{1})EF+F^{2}},\\\pi_{2}&=&\lambda_{2}c_{2}L_{3}\frac{(\lambda_{1}+\mu_{1})E+F}{c_{1}\mu_{1}E^{2}+(c_{1}+\lambda_{1}+\mu_{1})EF+F^{2}},\\\pi_{3}&=&c_{2}L_{3}\frac{(\lambda_{1}+\mu_{1})\mu_{2}E+c_{1}\mu_{1}E+(c_{1}+\mu_{2})F}{c_{1}\mu_{1}E^{2}+(c_{1}+\lambda_{1}+\mu_{1})EF+F^{2}},\\\pi_{4}&=&\lambda_{1}c_{1}L_{2}\frac{(c_{2}+\lambda_{2}+\mu_{2})E-F}{c_{1}\mu_{1}E^{2}+(c_{1}+\lambda_{1}+\mu_{1})EF+F^{2}},\\\pi_{5}&=&\lambda_{1}c_{1}L_{3}\frac{(\lambda_{2}+\mu_{2})E-F}{c_{1}\mu_{1}E^{2}+(c_{1}+\lambda_{1}+\mu_{1})EF+F^{2}},\\\pi_{6}&=&c_{1}L_{2}\frac{(c_{2}+\lambda_{2}+\mu_{2})\mu_{1}E+\mu_{2}c_{2}E-\mu_{1}F}{c_{1}\mu_{1}E^{2}+(c_{1}+\lambda_{1}+\mu_{1})EF+F^{2}},\\\pi_{7}&=&c_{1}L_{3}\frac{(\lambda_{2}+\mu_{2})\mu_{1}E+\mu_{2}c_{2}E-(c_{2}+\mu_{1})F}{c_{1}\mu_{1}E^{2}+(c_{1}+\lambda_{1}+\mu_{1})EF+F^{2}},\end{array} $$

where

$$ \begin{array}{rll} E&=&c_{1}+c_{2}+\lambda_{1}+\lambda_{2}+\mu_{1}+\mu_{2}, \\ F&=&c_{2}\mu_{2}-c_{1}\mu_{1}.\end{array} $$

Then, \(P(1;0,1)=\pi _{5}\) and \(P(1;1,1)=\pi _{7}\) are obtained and \(T_{s}=\frac {1}{c_{2}[P(1;0,1)+P(1;1,1)]}\) can be calculated. □

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, J., Li, J. & Howard, P.K. A system model of work flow in the patient room of hospital emergency department. Health Care Manag Sci 16, 341–351 (2013). https://doi.org/10.1007/s10729-013-9235-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10729-013-9235-1

Keywords

Search

Navigation