Examining the discharge practices of surgeons at a large medical center

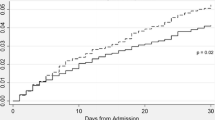
Abstract

We investigate the discharge practices at a large medical center. Specifically, we look for indications that patients are being discharged sooner because of hospital bed-capacity constraints. Using survival analysis techniques, we find statistically significant evidence to indicate that surgeons adjust their discharge practices to accommodate the surgical schedule and number of available recovery beds. We find higher discharge rates on days when utilization is high. We also find an increased discharge rate on days when more surgeries are scheduled. Our findings suggest that discharge decisions are made with bed-capacity constraints in mind. We discuss possible explanations for this, as well as the medical and managerial implications of our findings.

Appendices

Appendix A: Description of the Singer-Willett Method

Singer and Willett [10] provide a way of handling discrete time survival data using logistic regression. They extend the traditional Cox proportional hazards model to discrete time by allowing the use of logistic regression to estimate the hazard rate at each day as a function of the specified covariates. We describe their methodology.

Consider a homogeneous population of individuals, each at risk of experiencing a certain event (e.g., being discharged from a hospital). For each individual, the data includes a set of covariates, or predictors (for our problem, age, elective, surgical tract, measures of downstream bed utilization,…) that can, but do not necessarily, vary with time. The time until the event occurs, or until the individual drops out of the sample without the event occurring, is given in the data set. The event occurrence is then recorded into discrete intervals, which must be the same for each individual. A variable is then defined for each time period as 1 if the event happens during that interval and 0 otherwise. Because the event can only happen once for each individual, each occurrence is inherently conditional on all of the preceding time periods. If the event happens in period N, it cannot have happened in periods in {N-1, N-2, …,1}. For example, if a patient is discharged after seven days, then the patient was not discharged on days one to six.

A random variable T indicates the day that the patient is discharged. Because event occurrence is conditional, T is characterized by its conditional probability distribution, i.e., the distribution of the probability that an event will happen on a certain day, given that it has not already occurred. This distribution gives the discrete time hazard for each time period, h _j , or probability that the event will occur in time period j given that it has not already occurred

$$ {h_j} = \Pr \left[ {T = j\left| {T \geqslant j} \right.} \right]. $$

These discrete time hazards completely describe the distribution of time to event and average length of stay. The set of discrete time hazards is called the hazard function. The central focus of this method is estimating the effects of independent variables on the hazard function.

Now, consider the set of P predictors, Z _p (p = 1,2, …,P), each of which describes the members of the population on a specific characteristic. As some of these values can vary with time, the predictors are recorded for every time period. Each of the P predictors for individual i in time period j is denoted by the vector z _ij  = [z _1ij , z _2ij ,…, z _Pij ]. To account for heterogeneity in the population, an index for each member of the population is added to the hazard function, now denoted h _ij . The variable h _ij measures the probability that, for individual i, the event will occur on day j, given the vector of predictors for the individual and that the event has not yet occurred. The hazard function now becomes

$$ {h_j} = \Pr \left[ {{T_i} = j\left| {T \geqslant j} \right.,{Z_{{1ij}}} = {z_{{1ij}}},{Z_{{2ij}}} = {z_{{2ij}}}, \ldots, {Z_{{Pij}}} = {z_{{Pij}}}} \right]. $$

This equation indicates that the hazard is dependent on the values of the predictors, but does not specify the functional form of the dependency. Because the hazards are probabilities, a common proposition is that the hazards have a logistic dependence on the predictors and the time periods. This model represents the log-odds of event occurrence as a function of the parameters and time period. The proposed model to be estimated is

$$ \frac{1}{{1 + {e^{{\left[ {\left( {{\alpha_1}{D_{{1ij}}} + {\alpha_2}{D_{{2ij}}} + \cdots + {\alpha_J}{D_{{Jij}}}} \right) + \left( {{\beta_1}{Z_{{1ij}}} + {\beta_2}{Z_{{2ij}}} + \cdots {\beta_p}{Z_{{pij}}}} \right)} \right]}}}}} $$

where [D _1ij , D _2ij , … , D _Jij ] are dummy variables indexing time periods, and J is the last time period observed for anyone in the sample. These dummies are defined identically for every individual and every day, such that D _Nij  = 1 during time period N, and 0 at all other times. As shown below, the intercept parameters, [α ₁ , α ₂ , …, α _J ] measure the baseline hazard and the slope parameters, [β ₁ , β ₂ , _…, β _J ], define the effects of the predictors on the hazard function. The regression equation that is estimated is

$$ {\text{logi}}{{\text{t}}_e}\left( {{h_{{ij}}}} \right) = \left[ {\left( {\left( {{\alpha_1}{D_{{1ij}}} + {\alpha_2}{D_{{2ij}}} + \cdots + {\alpha_j}{D_{{2ij}}}} \right) + \left( {{\beta_1}{Z_{{1ij}}} + {\beta_2}{Z_{{2ij}}} + \cdots {\beta_p}{Z_{{pij}}}} \right)} \right.} \right. $$

where D is the vector of daily dummy variables, and Z is the vector of predictor variables.

This function can be estimated easily using logistic regression. However, the outcomes are conditional, and therefore autocorrelated, and traditional logistic regression assumes that each observation is independent and identically distributed. Because our data set violates that assumption, traditional logistic regression might not be valid. Singer and Willett prove that the likelihood function for the discrete time hazard process is identical to that of a series of independent Bernoulli trials. Because the response variables have a distribution that is identical to the distribution of independent Bernoulli trials, logistic regression can be used to estimate the parameters for the hazard function.

Results from the Singer-Willett model are interpreted exactly the same as in a standard logistic regression model. However, instead of a standard intercept, the series of time period dummies measures the baseline hazard. The slope coefficients measure the increase in the odds ratio that the event will occur.

Appendix B: Discrete Time Survival Analysis Outputs

Table 2 Effect of the threshold definition on the magnitude and significance of the FULL parameter

Table 3 Utilization threshold survival model (AIC = 32619, pseudo R-squared = .3393)

Table 4 Utilization threshold model with surgical group control (AIC = 32619, pseudo R-squared = .3623)

Table 5 Continuous utilization model (AIC = 32619, pseudo R-squared = .3393)

Table 6 Day of week and surgical schedule model results (AIC = 32202, pseudo R-squared = .3496)