Abstract
The process of black hole evaporation resulting from the Hawking effect has generated an intense controversy regarding its potential conflict with quantum mechanics’ unitary evolution. A recent set of works by a collaboration involving one of us, have revised the controversy with the aims of, on one hand, clarifying some conceptual issues surrounding it, and, at the same time, arguing that collapse theories have the potential to offer a satisfactory resolution of the so-called paradox. Here we show an explicit calculation supporting this claim using a simplified model of black hole creation and evaporation, known as the CGHS model, together with a dynamical reduction theory, known as CSL, and some speculative, but seemingly natural ideas about the role of quantum gravity in connection with the would-be singularity. This work represents a specific realization of general ideas first discussed in Okon and Sudarsky (Found Phys 44:114–143, 2014) and a complete and detailed analysis of a model first considered in Modak et al. (Phys Rev D 91(12):124009, 2015).





Similar content being viewed by others
Notes
Strictly speaking, as the example is two dimensional, what fluctuates is not really the signature, but the specific directions that are time-like and space-like.
More precisely, objective collapse models negate the assumption that all dynamical elements of the theory evolve according to a set of deterministic dynamical equations (private communication with Prof. P. Pearle). The subtlety refers to the fact that such models involve stochastic elements entering into the evolution equation of the quantum state, but of course, when those elements acquire specific values, the evolution of the quantum state of system is completely determined. However the specific values of those stochastic elements are not only a priori unkown, but they are, in principle, a priori unknowable.
Although there are two subtle differences, namely, (i) the dilaton potentials are different in these two models, thereby making different impacts on technical details and, (ii) the scalar field couples with the dilaton in the spherical collapse, whereas it is uncoupled to that in the CGHS model.
The precise study of this question will be left for future work.
The thermal coefficients that appear in the form of the density matrix operator \(\rho ^{in}_R\) come from the explicit form of the Bogolubov coefficients evaluated at late time limit, which fits our purposes in this work. However, for the CGHS model they can be determined without taking this limit [59].
For a extensive discussion of quantum fields on two dimensional black holes see, for instance, [59].
We thank R. Wald for a very informative discussion regarding this issue.
As we will see later, one envisions a truly fundamental theory of collapse that involves a general rule determining such operator in all situations, in terms of the fundamental physical degrees of freedom, i.e. the fields of the standard model and, in order to be really universal, in term of whatever is the fundamental quantum description of gravity at the quantum level.
B(t) corresponds to the Wiener process appearing in the corresponding Langevin equation in the standard treatment of Brownian motion.
Even though in regions (such as the black hole (BH) interior) where one does not have a time-like Killing field (KF) and thus one cannot rigorously talk about the conserved energy of a classical particle, when one has a KF which is time like in some other region, the conservation law associated with it can be used to extend the characterization in terms of “energy” of classical particles localized where the KF is not time-like. That is how one talks, for instance, about the negative energy of a particle inside the ergosphere of a Kerr BH. In fact, conservation laws even allow sometimes the effective use of the notion in order to make predictions that are relevant for observers in the asymptotic region. One can thus talk about the “time” KF inside the horizon of a Schwarzschild space-time \( t^a \) (the field associated with Schwarzschild coordinate t suitably extended to the black hole interior) although, in this region, this KF is not time-like. One can use the behavior of a certain mode of a quantum field in the black hole interior and call it (in an abuse of language) its “energy” according to asymptotic observers that see the BH at “rest” ( i.e. one can take the operator \( i t^a \nabla _a \) and apply it to the field mode as a way to characterize it, even if the mode is fully located in the BH interior). This scheme allows us to characterize the particular modes we have used in the BH interior, although no further physical significance is being attached to this characterization.
Using the Klein–Gordon inner product the operator \((N^{int}_{R})_{nj}\) can be expressed in terms of the field \(\hat{f}\) as a product of integrals over some arbitrary Cauchy hypersurfaces as:
$$\begin{aligned} (N^{int}_{R})_{nj}&= \hat{\tilde{b}}^{R\,\dagger }_{nj} \hat{\tilde{b}}^{R}_{nj}= \int _\Sigma d\Sigma \int _{\Sigma '} d\Sigma ' n^\mu n^{\nu \prime } \Big ( \tilde{v}_{nj} \tilde{v}_{nj}^{*\prime } \nabla _\mu \hat{f}^\dagger \nabla _\nu \hat{f}' -\tilde{v}_{nj}( \nabla _\nu \tilde{v}_{nj}^{*\prime }) (\nabla _\mu \hat{f}^\dagger ) \hat{f}' \\&\quad -\tilde{v}_{nj}^{*\prime } (\nabla _\mu \tilde{v}_{nj} ) \hat{f}^\dagger \nabla _\nu \hat{f}' + (\nabla _\mu \tilde{v}_{nj} ) (\nabla _\nu \tilde{v}_{nj}^{*\prime } ) \hat{f}^\dagger \hat{f}' \Big ) \end{aligned}$$(73)where, in an abuse of notation, we have dropped the superscript R on the modes. The out field operator \(\hat{f}\) is defined in Eq. (26) and the modes have been discretized as in Eq. (30). Note, however, that the \(\tilde{v}_{nj}\) modes have support only inside the horizon.
If it turns out to be the case that strong curvature expedites quantum collapse of wave function, it will of course be a strong evidence in favor of our proposal that information is indeed lost in black hole evaporation in the manner we have exemplified with this example. This in fact makes our proposal, in principle, susceptible to empirical investigation and that is an advantage over various models that have been put forward in this context so far.
At this point one could imagine instead just one system in a given initial state, and consider the ensemble of all alternative evolutions as represented by the density matrix. Although there is, in principle, nothing wrong with such view, we will not adopt it here, as we feel it could more easily lead to conceptual confusions.
The integral is carried out assuming \(\gamma =1 \) in Eq. (77). However, one can do it for other values of \(\gamma \ge 1\) with a similar conclusion.
We are of course referring to an EPR situation where a \(j=0\) system decays into two spin 1 / 2 particles along a certain axis and one considers two observers, Alice and Bob who can decide to measure the projection of the spin of the particle that reaches each one, along various different directions.
Private discussion with Prof. George Matsas.
Recall that the Tomonaga–Schwinger equation \( i \delta \left| \Psi (\Sigma ) \right\rangle = {\mathcal {H}}_I(x)\left| \Psi (\Sigma ) \right\rangle \delta \Sigma (x)\) gives the change in the interaction picture for the state associated with the corresponding hyper surfaces \(\Sigma '\) and \(\Sigma \), when the former is obtained from the latter by an infinitesimal deformation with four volume \(\delta \Sigma (x)\) around the point x in \(\Sigma \). We are ignoring here the formal aspects that indicate that strictly speaking the interaction picture does not exist.
Our references to “the horizon” within the setting where the singularity has been repaved by the “quantum gravity region”, should be taken to indicate the boundary of the past domain of dependence of said region.
In fact, this issue should arise in all schemes which, at the ensemble level, are described by a Lindblad equation, which is designed to ensure energy conservation. That is the equation defining the evolution of the density matrix is similar to that in (61) and involves operators A which commute with the hamiltonian, ensuring that \(\bar{\langle H \rangle } \) remains constant in time. However in all the cases, such as the situation at hand, where this equation arises from an “unraveling”, capable of describing the individual instances of evolution of a single system (see for instance [91], and references therein), in terms of some stochastic variable, the question as to whether energy is conserved in each individual case would become an open one. In fact, general considerations suggest that energy conservation would be violated, but in a manner which might be loosely associated with the time energy uncertainty relation, There seems to be some disagreement regarding the precise nature of the time-energy uncertainty relation. see for instance [92], and references therein.
By available degrees of freedom for a subsystem, we are referring, schematically, to the collection of quantum states \(\lbrace \left| \xi _i \right\rangle \rbrace \) of the subsystem in question which could, conceivably, be a relevant part of the expansion of the complete, pure, state of the full system in the form \(\Sigma _{ij} c_{ij} \left| \xi _i \right\rangle \left| \chi _j \right\rangle \) where \(\lbrace \left| \chi _j \right\rangle \rbrace \) are the states characterizing of the reminder of the system.
Private discussion with Prof. Alejandro Perez.
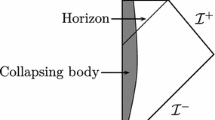
Also, just to distinguish we assume all points x belong to the exterior region II (Fig. 1) and \(\tilde{x}\) is defined in the interior (region III).
Here we use the redefinition \(x=x^- + \Delta .\)
References
Okon, E., Sudarsky, D.: Benefits of objective collapse models for cosmology and quantum gravity. Found. Phys. 44, 114–143 (2014)
Modak, S.K., Ortz, L., Pea, I., Sudarsky, D.: Non-paradoxical loss of information in black hole evaporation in a quantum collapse model. Phys. Rev. D 91(12), 124009 (2015)
Hawking, S.W.: Particle creation by black holes. Commun. Math. Phys. 43, 199 (1975) [Erratum-ibid. 46, 206 (1976)]
Hawking, S.W.: Breakdown of predictability in gravitational collapse. Phys. Rev. D 14, 2460 (1976)
Okon, E., Sudarsky, D.: The black hole information paradox and the collapse of the wave function. arXiv:1406.2011 [gr-qc]
Maldacena, J.M.: The large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 2, 231 (1998). [ hep-th/9711200]
Maldacena, J.M.: Eternal black holes in anti-de Sitter. JHEP 0304, 021 (2003). [ hep-th/0106112]
Strominger, A.: The dS/CFT correspondence. JHEP 0110, 034 (2001). [ hep-th/0106113]
Kachru, S., Liu, X., Mulligan, M.: Gravity duals of Lifshitz-like fixed points. Phys. Rev. D 78, 106005 (2008). arXiv:0808.1725 [hep-th]
Almheiri, A., Marolf, D., Polchinski, J., Sully, J.: Black holes: complementarity or firewalls? JHEP 1302, 062 (2013). arXiv:1207.3123 [hep-th]
Maldacena, J., Susskind, L.: Cool horizons for entangled black holes. Fortsch. Phys. 61, 781 (2013). arXiv:1306.0533 [hep-th]
Rovelli, C., Vidotto, F.: Planck stars. arXiv:1401.6562 [gr-qc]
Mathur, S.D.: The information paradox: a pedagogical introduction. Class. Quant. Grav. 26, 224001 (2009). arXiv:0909.1038 [hep-th]
Mathur, S.D.: How fuzzballs resolve the information paradox. J. Phys. Conf. Ser. 462, 012034 (2013)
Bojowald, M.: Absence of singularity in loop quantum cosmology. Phys. Rev. Lett. 86, 5227 (2001) [ gr-qc/0102069]
Ashtekar, A., Bojowald, M.: Quantum geometry and the Schwarzschild singularity. Class. Quant. Grav. 23, 391–411 (2006)
Ashtekar, A., Taveras, V., Varadarajan, M.: Information is not lost in the evaporation of 2-dimensional black holes. Phys. Rev. Lett. 100, 211302 (2008). arXiv:0801.1811 [gr-qc]
Bojowald, M.: Information loss, made worse by quantum gravity. arXiv:1409.3157 [gr-qc]
d’Espagnat, B.: Conceptual Foundations of Quantum Mechanics, 2nd edn. Addison-Wesley, Boston (1976)
Albert, D.: Quantum Mechanics and Experience. Harvard University Press, Cambridge (1992). Chapters 4 and 5
Bell, J.: Quantum mechanics for cosmologists. In: Quantum Gravity II. Oxford University Press, Oxford (1981)
Home, D.: Conceptual Foundations of Quantum Physics: An Overview from Modern Perspectives, Chapter 2. Plenum, New York (1997)
Wigner, E.: The problem of measurement. Am. J. Phys. 31, 6 (1963)
Lagget, A.: Macroscopic quantum systems and the quantum theory of measurement. Prog. Theor. Phys. Suppl. 69, 80 (1980)
Penrose, R.: The Emperor’s New Mind. Oxford University Press, Oxford (1989)
Penrose, R.: On Gravity’s Role in Quantum State Reduction. In: Callender, C. (ed.) Physics meets philosophy at the Planck scale. Cambridge University Press, Cambridge (2001)
Jammer, M.: Philosophy of Quantum Mechanics. The Interpretations of Quantum Mechanics in Historical Perspective. Wiley, New York (1974)
Omnes, R.: The Interpretation of Quantum Mechanics. Princeton University Press, Princeton (1994)
Adler, S.L.: Why Decoherence has not Solved the Measurement Problem: A Response to PW Anderson. Stud. Hist. Philos. Mod. Phys. 34, 135–142 (2003). arXiv:quant-ph/0112095
Bassi, A., Ghirardi, G.C.: Dynamical reduction models. Phys. Rep. 379, 257 (2003). arXiv:quant-ph/0302164
Ghirardi, G.: Collapse Theories. The Stanford Encyclopedia of Philosophy (Winter 2011 Edition), Edward N. Zalta (ed.). http://plato.stanford.edu/archives/win2011/entries/qmcollapse/ (2011). Accessed 1 Aug 2015
Ghirardi, G.: Bohm’s theory versus dynamical reduction. In: Cushing, J.T., et al. (eds.) Bohmian Mechanics and Quantum Theory: An Appraisal, pp. 353–377. Kluwer Academic Publishers, Berlin (1996)
Durr, D., Goldstein, S., Zangh, N.: Bohmian mechanics and the meaning of the wave function. In: Cohen, R.S., Horne, M., Stachel, J. (eds.) Experimental Metaphysics-Quantum Mechanical Studies for Abner Shimony, Volume One; Boston Studies in the Philosophy of Science 193. Kluwer Academic Publishers, Berlin (1997)
Bell, J.S.: On the impossible pilot wave. Found. Phys. 12, 989–999 (1982)
Wallace, D.: The Emergent Multiverse. Oxford University Press, Oxford (2012)
Fuchs, C., Peres, A.: Quantum theory needs no ‘interpretation’. Phys. Today 53(3), 70–71 (2000)
Lombardi, O., Dieks, D.: Modal Interpretations of Quantum Mechanics. The Stanford Encyclopedia of Philosophy, Stanford (2014)
Joos, E., et al.: Decoherence and the Appearance of a Classical World in Quantum Theory, 2nd edn. Springer, Berlin (2003)
Zurek, W.: Decoherence and the transition from quantum to classical. Phys. Today 44(10) (1991)
Kent, A.: Against Many-Worlds Interpretations. http://xxx.arxiv.org/abs/gr-qc/9703089
Brown, H., Wallace, D.: Solving the measurement problem: de Broglie-Bohm loses out to Everett. Found. Phys. 35, 517–540 (2005)
Bub, J.: Interpreting the Quantum World, chapter 8, pp. 212–236. Cambridge (1997). (Rather critical discussion of the decoherence-based approaches)
Bell, J.S.: Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press, Cambridge (1987)
Bell, J.S.: Against ‘measurement. Phys. World 3, 33 (1990)
Maudlin, T.: Three measurement problems. Topoi 14(1), 715 (1995)
Bohm, D., Bub, J.: A proposed solution of the measurement problem in quantum mechanics by a hidden variable theory. Rev. Mod. Phys. 38, 453 (1966)
Pearle, P.: Reduction of the state vector by a nonlinear Schrödinger equation. Phys. Rev. D 13, 857 (1976)
Ghirardi, G., Rimini, A., Weber, T.: A model for a unified quantum description of macroscopic and microscopic systems. In: Accardi, A.L. (ed.) Quantum Probability and Applications, pp. 223–232. Springer, Heidelberg (1985)
Ghirardi, G., Rimini, A., Weber, T.: Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 34, 470 (1986)
Pearle, P.: Combining stochastic dynamical state-vector reduction with spontaneous localization. Phys. Rev. A 39, 2277–2289 (1989)
Ghirardi, G., Pearle, P., Rimini, A.: Markov-processes in Hilbert-space and continuous spontaneous localization of systems of identical particles. Phys. Rev. A 42, 7889 (1990)
Bassi, A., Lochan, K., Satin, S., Singh, T., Ulbricht, H.: Models of wave-function collapse, underlying theories, and experimental tests. Rev. Mod. Phys. 85, 471 (2013)
Pearle, P.: Collapse models. arXiv:quant-ph/9901077
Pearle, P.: Collapse Miscellany. arXiv:1209.5082 [quant-ph]
Callan, C.G., Giddings, S.B., Harvey, J.A., Strominger, A.: Evanescent black holes. Phys. Rev. D 45, R1005 (1992)
Giddings, S.B.: Quantum mechanics of black holes. arXiv:hep-th/9412138v1
Strominger, A.: Les Houches Lectures on Black Holes. arXiv:hep-th/9501071v1
Benachenhou, F.: Black hole evaporation: a survey. hep-th/9412189
Fabbri, A., Navarro-Salas, J.: Modeling Black Hole Evaporation. Imperial College Press, London (2005)
Susskind, L., Thorlacius, L.: Hawking radiation and back-reaction. Nucl. Phys. B 382, 123–147 (1992)
Russo, J.G., Susskind, L., Thorlacius, L.: The endpoint of Hawking radiation. Phys. Rev. D 46, 3444 (1992)
Ashtekar, A., Pretorius, F., Ramazanoglu, F.M.: Evaporation of 2-Dimensional Black Holes. Phys. Rev. D 83, 044040 (2011). arXiv:1012.0077 [gr-qc]
Kuchar, K.V., Romano, J.D., Varadarajan, M.: Dirac constraint quantization of a dilatonic model of gravitational collapse. Phys. Rev. D 55, 795 (1997). gr-qc/9608011
Varadarajan, M.: Quantum gravity effects in the CGHS model of collapse to a black hole. Phys. Rev. D 57, 3463 (1998). gr-qc/9801058
Giddings, S.B., Nelson, W.M.: Quantum emission from two-dimensional black holes. Phys. Rev. D 46, 2486 (1992)
Davies, P.C.W., Fulling, S.A., Unruh, W.G.: Energy-momentum tensor near an evaporating black hole. Phys. Rev. D 13, 2720 (1976)
Hiscock, W.A.: Models of evaporating black holes. I. Phys. Rev. D 23, 2813 (1981)
Parker, L., Toms, D.: Quantum Field Theory in Curved Spacetime. Cambridge University Press, Cambridge (2007)
Wald, R.M.: Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics. The University of Chicago Press, Chicago (1994)
Aspect, A., Grangier, P., Roger, G.: Experimental realization of Einstein–Podolsky–Rosen–Bohm Gedanken experiment: a new violation of Bell’s inequalities. Phys. Rev. Lett. 49, 91 (1982)
Penrose, R.: Singularities and time-asymmetry. In: Hawking, S.W., Israel, W. (eds.) General Relativity: An Einstein Centenary Survey, pp. 581–638. Cambridge University Press, Cambridge (1979)
Pearle, P.: Toward a relativistic theory of statevector reduction. In: Miller, A. (ed.) Sixty-Two Years of Uncertainty, pp. 193–214. Plenum, New York (1990)
Ghirardi, G., Grassi, R., Pearle, P.: Relativistic dynamical reduction models: general framework and examples. Found. Phys. (J.S. Bell’s 60th birthday issue) 20, 1271 (1990)
Tumulka, R.: A relativistic version of the Ghirardi–Rimini–Weber model. J. Stat. Phys. 125, 821 (2006)
Tumulka, R.: On spontaneous wave function collapse and quantum field theory. Proc. R. Soc. A 462, 1897 (2006)
Bedingham, D.J.: Relativistic state reduction model. J. Phys. Conf. Ser. 306, 012034 (2011)
Bedingham, D.J.: Relativistic state reduction dynamics. Found. Phys. 41, 686 (2011)
Pearle, P.: A Relativistic Dynamical Collapse Model. arXiv:1412.6723 [quant-ph]
Banks, T., Susskind, L., Peskin, M.E.: Difficulties for the evolution of pure states into mixed states. Nucl. Phys. B 244, 125 (1984)
Unruh, W.G., Wald, R.M.: On evolution laws taking pure states to mixed states in quantum field theory. Phys. Rev. D 52, 2176–2182 (1995)
Penrose, R.: Time asymmetry and quantum gravity. In: Isham, C.J., Penrose, R., Sciama, D.W. (eds.) Quantum Gravity II, p. 244. Oxford University Press, Oxford (1981)
Perez, A., Sahlmman, H., Sudarsky, D.: On the quantum mechanical origin of the seeds of cosmic structure. Class. Quant. Grav. 23, 2317 (2006)
Sudarsky, D.: Shortcomings in the understanding of why cosmological perturbations look classical. Int. J. Modern Phys. D 20, 509 (2011). arXiv:0906.0315 [gr-qc]
Landau, S.J., Scoccola, C.G., Sudarsky, D.: Cosmological constraints on nonstandard inflationary quantum collapse models. Phys. Rev. D 85, 123001 (2012). arXiv:1112.1830 [astro-ph.CO]
León García, G., Landau, S.J., Sudarsky, D.: Quantum origin of the primordial fluctuation spectrum and its statistics. Phys. Rev. D 88, 023526 (2013). arXiv:1107.3054 [astro-ph.CO]
Diez-Tejedor, A., Sudarsky, D.: Towards a formal description of the collapse approach to the inflationary origin of the seeds of cosmic structure. JCAP 045, 1207 (2012). arXiv:1108.4928 [gr-qc]
Cañate, P., Pearle, P., Sudarsky, D.: CSL quantum origin of the primordial fluctuation. Phys. Rev. D 87, 104024 (2013). arXiv:1211.3463[gr-qc]
Décanini, Y., Folacci, A.: Hadamard renormalization of the stress-energy tensor for a quantized scalar field in a general spacetime of arbitrary dimension. Phys. Rev. D 78, 044025 (2008)
Salehi, H., Bisabr, Y.: Hadamard states and two-dimensional gravity. Int. J. Mod. Phys. A 16, 3699 (2001)
Synge, J.L.: Relativity: The General Theory. North-Holland Publishing Company, Amsterdam (1971)
Diosi, L., Gisin, N., Strunz, W.T.: Non-Markovian quantum state diffusion. Phys. Rev. A 58, 1699 (1998)
Aharonov, Y., Oppenheim, J., Popescu, S., Reznik, B., Unruh, W.G.: Measurement of time of arrival in quantum mechanics. Phys. Rev. A 57, 4130 (1998)
Israel, W.: Singular hypersurfaces and thin shells in general relativity. Nuovo Cim. B44, 1 (1966); Erratum-ibid. B48, 463 (1967)
Page, D.N., Geilker, C.D.: Phys. Rev. Lett. 47, 979 (1981)
Carlip, S.: Is quantum gravity necessary? Class. Quant. Grav. 25, 154010 (2008)
Bedingham, D.J.: Dynamical state reduction in an EPR experiment. arXiv:0907.2327 [quant-ph]
Ghirardi, G.C.: Properties and events in a relativistic context: revisiting the dynamical reduction program. Found. Phys. Lett. 9, 313 (1996)
Ghirardi, G.C., Rimini, A., Weber, T.: A general argument against superluminal transmission through the quantum mechanical measurement process. Letter Al Nuovo Cimento 27, 293 (1980)
Ghirardi, G.C., Grassi, R., Butterfield, J., Fleming, G.N.: Parameter dependence and outcome dependence in dynamic models for state-vector reduction. Found. Phys. 23, 341 (1993)
Ghirardi, G.C., Grassi, R.: Outcome predictions and property attribution: the EPR argument reconsidered. Stud. History Philos. Modern Phys. 25, 397 (1994)
Acknowledgments
We acknowledge useful discussions with Robert Wald, Elias Okon, Philip Pearle, Bernard Kay, George Matsas, Alejandro Perez and the participants of the meeting “Haunted Workshop: Who is afraid of Quantum Theory?”, Tepoztlán, México, 2013. IP thanks ICN-UNAM for providing visiting facilities during his sabbatical year when part of this work was done. Two of the authors, SKM and LO, are supported by DGAPA postdoctoral fellowships from UNAM. We acknowledge partial financial support from DGAPA-UNAM projects IN107412 (DS), and CONACyT project 101712 (DS).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Non-Hadamard behavior in the \(\varvec{out}\) region
In this section we shall follow the standard Hadamard prescription to prove the non-Hadamard behavior of an arbitrary particle state (including the zero particle state, i.e, vacuum) in the out quantization defined in the case of evaporating black hole.
1.1 The two-point function
We use the discrete basis by working with wave packets. In this basis the modes are orthonormalized unlike the continuous counterpart. The field operator has the following form
In the above expression we again used tilde to denote that these modes are defined interior to the black hole.Footnote 24 The wave packets defined exterior to black hole, similar to Eq. (30), are given by
where the modes \(v_{\omega }^{L/R}\) are given in Eq. (109) and Eq. (111). Below we provide an explicit calculation only for the right-moving modes since the other left-moving sector is fully analogous.
We calculate the two-point function in an arbitrary state, say, \(\left| \psi \right\rangle =\left| F \right\rangle ^{int}\otimes \left| F \right\rangle ^{ext}\) of the joint basis. The two-point function takes the following form
Note that the contributions from the exterior (region II, Fig. 1) and interior (region III, Fig. 1) of the black hole decouples from one another. Let us first focus on the first term defined exterior. Calculations involving the other term defined in the interior to the black hole is exactly similar. Writing this term explicitly yields
while the other terms do not contribute. The next step would be to use the commutator relation between the creation and annihilation operators and orthonormality condition \(\left\langle F_{nj} \right| {F_{n'j'}}\rangle ^{ext} = \delta _{nn'}\delta _{jj'}\). This simplifies Eq. (96) to the following form
where,
In the expression Eq. (97), the integration over the term that includes \(F_{nj}\) gives
Note that since \(\left| F \right\rangle ^{ext}\) is a well defined state in the out Fock space it may have arbitrary number of particles but in no case it can be infinity. Therefore not all \(F_{nj}\)-s are nonzero when n and j are changing their values. On the other hand the term without \(F_{nj}\) in Eq. (97) can be simplified in the following manner. We first use the identity
As a result the integrations of the two integrals over \(\omega \) and \(\omega '\) transforms into a single integral, and then, by appropriately using the definition of the function \(\gamma \) to turn the the sum over j into an integral, we obtain the final expression for the two-point function
In order to check the Hadamard behavior, as explained in Sect. 3.3, we need to construct the symmetrized two-point function
and subtract the “Hadamard ansatz”. If the quantum state is Hadamard then we expect no singular behavior after the above said subtraction.
1.2 The Hadamard Ansatz
In two dimensions it seems to be a non-agreement about precise form of the “Hadamard ansatz” [88] and [89]. Usually the differences in opinion comes through the finite terms that are present in the Hadamard ansatz. Nevertheless, for our purpose we are interested to extract the singular behavior due to coincidence limit. We restrict to the following singular behavior of the Hadamard ansatz
where \(\sigma \) is half of the geodesic distance square between two close points x and \(x'\) in the normal neighborhood.
Now let us proceed to calculate the geodesic distance between x and \(x'\). We will do it in null coordinates. The calculations of this section are based on section 2 of chapter II of [90]. The geodesic distance is given by
where \(u_{1}\) is the affine parameter of the geodesic at \(x'\), \(U^{\mu '}=\frac{dx}{du}\) is the tangent vector to the geodesic and \(g_{\mu '\nu '}\) is the metric of space-time. Now we use that
where \(\xi ^{\mu }=x^{\mu }-x^{\mu '}\) and \(\Gamma ^{\mu '}_{\alpha '\beta '}\) are the usual Christoffel symbols. By using Eq. (106) in Eq. (105) we obtain
Up to cubic order in \(\xi ^{\mu }\) we obtain
Now we find that the only Christoffel symbols different from zero areFootnote 25
where \(\Omega =\frac{1}{\frac{M}{\Lambda }-xx^{+}\Lambda ^{2}}\) and \(g_{xx^{+}}=g_{x^{+}x}=-\frac{1}{2}\Omega \). Then the geodesic distance is given by
This simplifies to
Using Eq. (109) and the expression for the metric in Eq. (111) we finally obtain
where \(\Delta x=x'-x\) and \(\Delta x^{+}=x'^{+}-x^{+}\). This geodesic distance is clearly an approximation, but for our purposes is seems to be enough.
1.3 The non-Hadamard behavior
In order to check the Hadamard property we substitute Eq. (112) in Eq. (104) and subtract the result from Eq. (102). We obtain the following expression
Note that with the above expression for the renormalized two-point function we have a well defined coincidence limit with x and \(x'\). However while approaching the horizon \(x= x^- + \Delta =0\), there appears another divergence of the form \(\log x\) which is not of the Hadamard form. Therefore clearly the state \(|F\rangle ^{ext}\) is not Hadamard. Similarly one can prove that the particle state \(|F\rangle ^{int}\) is also non-Hadamard. This obviously implies that the states \(|F\rangle ^{int}\otimes |F\rangle ^{ext}\) of the joint Hilbert space is non-Hadamard.
Appendix 2: Proof of well defined foliation
The intersecting curves Eq. (65) and Eq. (66) are very important since they determine the foliation of the space-time. One might be concerned with the possibility that the foliating surfaces may cross each other at some region of the space-time. If this happens then one fails to associate a well defined evolution of the quantum states. Here we give a proof that such crossings among foliating surfaces does not take place.
The most general situation where this crossing can happen is shown on the left in Fig. 6. From the figure we can see that such crossings can take place both in regions II and III. Let us first consider the situation in region III. A zoomed version highlighting this aspect is shown on the right of Fig. 6. In the figure \(T_{r_1} (r_1, X)\) and \(T_{r_2}(r_2, X)\) are two \(r=const.\) curves and the points A and B are on curves \(T_{r_1}\) and \(T_{r_2}\) respectively. The slope of the line joining A and B is given by
This can be easily expressed in terms of the slopes of the line joining the points E with A and E with C such that
Now making use of the mean-value theorem and \(\Delta X = X_C - X _B \rightarrow 0\) we can associate the slope \(m_{BA}\) with the slope of the guiding curve (generated by all intersecting points) and \(m_{EA}\) with the curve \(T_{r_1}\). Then Eq. (115) clearly tells us that the slope of the guiding curve should be less than the slope of \(r=const.\) curve. But this is clearly in contradiction with our choice Eq. (65). Actually, it is trivial to verify that the slope of Eq. (65) is always greater than the slope of Eq. (64) provided \(r<r_h\). With this we rule out the crossing behavior showing in Fig. 6. Similarly, for region-II, in order to have a crossing it is necessary that the slope of the guiding curve is less that the \(t= const.\) curve. However, by comparing the slopes of Eq. (66) and Eq. (63) one can conclude that this situation does not appear given the condition \(X>T\) in region II.
Appendix 3: Useful integrals to define \(\zeta \)
Here we provide the explicit results of various integrals defined in Sect. 6. These integrals measure the distance of a point in a particular foliating hypersurface. This distance is the parameter \(\zeta \) Eq. (67) used together with \(\tau \) for locating a point in CGHS space-time.
Appendix 4: The SSC formalism and the sudden collapse of the quantum state
When one considers a description of a situation requiring a quantum treatment of matter fields and at the same time requires a classical picture of space-time, allowing the consideration of questions such as those that usually as arise in the context of the BHIP; one is in the realm of semi-classical gravity. As discussed in this can not considered as a truly fundamental characterization of the physical situation, but only as an effective description. Nevertheless it is convenient among other reasons for the sake of conceptual clarity to have a well defined framework, where various issues can be studied in a self consistent manner. This can be thought as analogous to, say, the Navier Stokes equation in hydrodynamics, which even though can not be considered as a fundamental description of a fluid, and which is known not to be valid under various kind of circumstances, leads to an internally self consistent description, that can be the subject of rigorous mathematical analysis. A scheme which is hoped to offer a similar characterization has been developed for semi-classical gravity, and it is defied as follows.
Definition
The set \(\left\{ g_{\mu \nu }(x),\hat{\varphi }(x),\hat{\pi }(x),{\mathscr {H}},\vert \xi \rangle \ in {\mathscr {H}}\right\} \) represents a Semiclassical Self-Consistent Configuration SSC if and only if \(\hat{\varphi }(x)\), \(\hat{\pi }(x)\) and \({\mathscr {H}}\) correspond to a quantum field theory constructed over a space-time with metric \(g_{\mu \nu }(x)\) (as described in, say [69]), and the state \(\vert \xi \rangle \) in \({\mathscr {H}}\) is such that
for all the points x in the space-time manifold.
The point however is that such rigid definition does not allow for the incorporation of something like a collapse of the quantum state of the matter fields. However we can extend the scheme by incorporating a transition from one SSC to a another associated to a sudden change in the state of the system, as an analog of the matching used in the treatment of thin shells in general relativity developed in [93]. That is, just as in the later case, one matches two space-times across a time-like boundary representing the thin matter shell, in the situation at hand, one matches two space-times across a space-like hypesurface taken to represent the excitation of the fundamental underlying DOF of quantum gravity that must occur in association with what we call the collapse of the quantum state of the matter fields.
The basic idea is then that a collapse is associated not just with the sudden transition from one state \(\vert \xi _1\rangle \) in \({\mathscr {H}}\) to another \(\vert \xi _2\rangle \) in \( {\mathscr {H}}\) but with a the transition of a complete SSC to another \( SSC_1 \rightarrow SSC_2\), which not only involves a jump in the state but also the jump in the space-time metric and even in the Hilbert space. The analysis performed in [86] indicates that the matching of space-times might be done while requiring continuity of the induced metric across the collapse hypersurfae, but allowing for a discountinuity of the extrinsic curvature.
The above scheme is clearly designed to deal with a single spontaneous collapse of the quantum state, but it seems in principle extendable to deal with proposals involving continuous reduction processes such as those considered in CSL.
It is clear however that further research on the details of these formalism as applied to theories like CSL is required.
Rights and permissions
About this article
Cite this article
Modak, S.K., Ortíz, L., Peña, I. et al. Black hole evaporation: information loss but no paradox. Gen Relativ Gravit 47, 120 (2015). https://doi.org/10.1007/s10714-015-1960-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10714-015-1960-y