A general method for constructing curved traversable wormholes in (2+1)-dimensional spacetime

Abstract

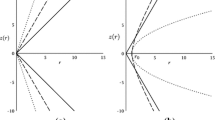
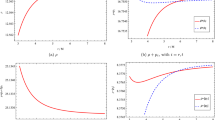
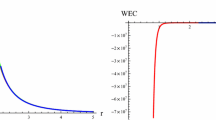
We develop a general method for constructing curved traversable wormholes in (2+1)-dimensional spacetime, by generating surfaces of revolution around smooth curves. Application of this method to a straight line gives the usual spherically symmetric wormholes. The physics behind (2+1)-d curved traversable wormholes is discussed based on solutions to the Einstein field equations when the tidal force is zero. The Einstein field equations are found to reduce to one equation whereby the mass-energy density varies linearly with the Ricci scalar, which signifies that our (2+1)-d curved traversable wormholes are supported by dust of ordinary and exotic matter without radial tension nor lateral pressure. With this, two examples of (2+1)-d curved traversable wormholes: the helical wormhole and the catenary wormhole, are constructed and we show that there exist geodesics through them supported by non-exotic matter. This general method is applicable to our (3+1)-d spacetime.

Appendix: some proofs

1.1 Proof of metric for surface of revolution generated around plane curves being free of spatial cross-term

Consider a unit-speed plane curve ${\varvec{\psi }}(v)=(f(v),g(v),0)$ where $f^{\prime }(v)$ and $g^{\prime }(v)$ (recall that prime denotes derivative with respect to $v$) are not simultaneously zero. A curve is unit-speed if its tangent vector has unit length, so that $f^{\prime }(v)^2+g^{\prime }(v)^2=1$. It is a theorem in elementary differential geometry that any smooth (or regular) curve can be reparametrised to be unit-speed [33], so it is sufficient to just consider unit-speed curves.

According to the method described in Sect. 2, the two orthonormal vectors are $\mathbf{{n}}(v)=(-g^{\prime }(v),f^{\prime }(v),0)$ and $\mathbf{{b}}(v)=(0,0,1)$. Hence the surface of revolution around ${\varvec{\psi }}(v)$ is

$$\begin{aligned} {\varvec{\sigma }}(u,v)=(f(v)-g^{\prime }(v)Z(v)\cos {u},g(v) +f^{\prime }(v)Z(v)\cos {u},Z(v)\sin {u}). \end{aligned}$$

(54)

Then, the partial derivatives of ${\varvec{\sigma }}$ are

$$\begin{aligned} {\varvec{\sigma }}_u(u,v)&= \left( \begin{array}{c} g^{\prime }(v)Z(v)\sin {u}\\ -f^{\prime }(v)Z(v)\sin {u}\\ Z(v)\cos {u}\\ \end{array}\right),\end{aligned}$$

(55)

$$\begin{aligned} {\varvec{\sigma }}_v(u,v)&= \left( \begin{array}{c} f^{\prime }(v)-g^{\prime }(v)Z^{\prime }(v)\cos {u}-g^{\prime \prime }(v)Z(v)\cos {u}\\ g^{\prime }(v)+f^{\prime }(v)Z^{\prime }(v)\cos {u}+f^{\prime \prime }(v)Z(v)\cos {u}\\ Z^{\prime }(v)\sin {u}\\ \end{array}\right). \end{aligned}$$

(56)

With this,

$$\begin{aligned} g_{uv}&= {\varvec{\sigma }}_u\cdot {\varvec{\sigma }}_v\end{aligned}$$

(57)

$$\begin{aligned}&= -Z(v)Z^{\prime }(v)\sin {u}\cos {u}\left[f^{\prime }(v)^2 + g^{\prime }(v)^2-1\right]\nonumber \\&-Z(v)^2\sin {u}\cos {u}\left[f^{\prime }(v)f^{\prime \prime } (v)+g^{\prime }(v)g^{\prime \prime }(v)\right]. \end{aligned}$$

(58)

From the unit-speed condition, the first term in $g_{uv}$ vanishes. Differentiating the unit-speed condition with respect to $v$ gives $f^{\prime }(v)f^{\prime \prime }(v)+g^{\prime }(v)g^{\prime \prime }(v)=0$, so that the second term also vanishes. This completes the proof.

In addition, note that $g_{uu}=Z(v)^2$, and also that $g_{vv}$ is in general a function of both spatial coordinates $u$ and $v$.

1.2 Proof of the 3-manifold of revolution around a straight line being spherically symmetric

A 3-manifold is said to be spherically symmetric if when expressed in spherical coordinates, its metric takes the form

$$\begin{aligned} ds^2=A(r)\ dr^2+r^2(d\theta ^2+\sin ^2{\theta }\ d\phi ^2), \end{aligned}$$

(59)

where $A(r)$ is some function of the radial coordinate [18].

Consider the straight line $\mathbf{l}(v)=(0,0,0,z(v))$ embedded in a 4-d Euclidean space. Following the technique described in Sect. 5 and taking the three orthonormal vectors mutually perpendicular to $\mathbf{l}(v)$ to be the directions along the other three coordinate axes $\mathbf{e}_1, \mathbf{e}_2$ and $\mathbf{e}_3$, the 3-manifold of revolution around $\mathbf{l}(v)$ is

$$\begin{aligned} {\varvec{\tau }}(w,u,v)=(Z(v)\cos {u},Z(v)\sin {u}\cos {w},Z(v) \sin {u}\sin {w},z(v)). \end{aligned}$$

(60)

Then, the partial derivatives of ${\varvec{\tau }}$ (prime in this section denotes derivative with respect to $w$) are

$$\begin{aligned} {\varvec{\tau }}_u&= \left( \begin{array}{c} -Z(v)\sin {u}\\ Z(v)\cos {u}\cos {w}\\ Z(v)\cos {u}\sin {w}\\ 0\\ \end{array} \right)\end{aligned}$$

(61)

$$\begin{aligned} {\varvec{\tau }}_v&= \left( \begin{array}{c} Z^{\prime }(v)\cos {u}\\ Z^{\prime }(v)\sin {u}\cos {w}\\ Z^{\prime }(v)\sin {u}\sin {w}\\ z^{\prime }(v)\\ \end{array} \right)\end{aligned}$$

(62)

$$\begin{aligned} {\varvec{\tau }}_w&= \left( \begin{array}{c} 0\\ -Z(v)\sin {u}\sin {w}\\ Z(v)\sin {u}\cos {w}\\ 0\\ \end{array}\right). \end{aligned}$$

(63)

The non-zero components of the metric tensor would be

$$\begin{aligned} g_{uu}=Z(v)^2, \quad g_{vv}=Z^{\prime }(v)^2+z^{\prime }(v)^2,\quad g_{ww}=Z(v)^2\sin ^2{u}, \end{aligned}$$

(64)

and so

$$\begin{aligned} ds^2=(Z^{\prime }(v)^2+z^{\prime }(v)^2)\ dv^2+Z(v)^2(du^2+\sin ^2{u}\ dw^2). \end{aligned}$$

(65)

A metric of this form can be considered to be spherically symmetric. Nevertheless, we shall make this explicit by expressing it in the form in Eq. (59). To do this, we will make the following reparametrisation $v=Z^{-1}(r), u=\theta$ and $w=\phi$. Under this reparametrisation, Eq. (60) becomes

$$\begin{aligned} {\varvec{\tau }}(r,\theta ,\phi )=(r\cos {\theta },r\sin {\theta }\cos {\phi }, r\sin {\theta }\sin {\phi },z(Z^{-1}(r))). \end{aligned}$$

(66)

The metric would then be

$$\begin{aligned} ds^2=\left(1+\left(\frac{d[z(Z^{-1}(r))]}{dr}\right)^2\right)\ dr^2+r^2(d\theta ^2+\sin ^2{\theta }\ d\phi ^2). \end{aligned}$$

(67)

The proof for an n-manifold of revolution around a straight line is similar.