The spectrum of simplicial volume of non-compact manifolds

Abstract

We show that, in dimension at least 4, the set of locally finite simplicial volumes of oriented connected open manifolds is $[0,\infty ]$. Moreover, we consider the case of tame open manifolds and some low-dimensional examples.

1 Introduction

Simplicial volumes are invariants of manifolds defined in terms of the $\ell ^1$-semi-norm on singular homology [9].

Definition 1.1

(simplicial volume) Let M be an oriented connected d-manifold without boundary. Then the simplicial volume of M is defined by

$$\begin{aligned} \Vert M \Vert ^{{{\,\mathrm{lf}\,}}} := \inf \bigl \{ |c|_1 \bigm | c \in C_d^{{{\,\mathrm{lf}\,}}}(M;{\mathbb {R}}) \text {is a fundamental cycle of}~M \bigr \}, \end{aligned}$$

where $C^{{{\,\mathrm{lf}\,}}}_*$ denotes the locally finite singular chain complex. If M is compact, then we also write $\Vert M\Vert := \Vert M \Vert ^{{{\,\mathrm{lf}\,}}}$. Using relative fundamental cycles, the notion of simplicial volume can be extended to oriented manifolds with boundary.

Simplicial volumes are related to negative curvature, volume estimates, and amenability [9]. In the present article, we focus on simplicial volumes of non-compact manifolds. Only few concrete results are known in this context: There are computations for certain locally symmetric spaces [3, 12, 15, 16] as well as the general volume estimates [9], vanishing results [8, 9], and finiteness results [9, 14].

Let $d \in {\mathbb {N}}$, let M(d) be the class of all oriented closed connected d-manifolds, and let $M^{{{\,\mathrm{lf}\,}}}(d)$ be the class of all oriented connected manifolds without boundary. Then we set ${{\,\mathrm{SV}\,}}(d) := \bigl \{ \Vert M\Vert \bigm | M \in M(d) \bigr \}$ and

$$\begin{aligned} {{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}(d)&:= \bigl \{ \Vert M \Vert ^{{{\,\mathrm{lf}\,}}} \bigm | M \in M^{{{\,\mathrm{lf}\,}}}(d) \bigr \}. \end{aligned}$$

It is known that ${{\,\mathrm{SV}\,}}(d)$ is countable and that this set has no gap at 0 if $d \ge 4$:

Theorem 1.2

[10, Theorem A] Let $d \in {\mathbb {N}}_{\ge 4}$. Then ${{\,\mathrm{SV}\,}}(d)$ is dense in ${\mathbb {R}}_{\ge 0}$ and $0 \in {{\,\mathrm{SV}\,}}(d)$.

In contrast, if we allow non-compact manifolds, we can realise all non-negative real numbers:

Theorem A

Let $d\in {\mathbb {N}}_{\ge 4}$. Then ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}(d) = [0,\infty ]$.

The proof uses the no-gap theorem Theorem 1.2 and a suitable connected sum construction.

If we restrict to tame manifolds, then we are in a similar situation as in the closed case:

Theorem B

Let $d\in {\mathbb {N}}$. Then the set ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(d) \subset [0,\infty ]$ is countable. In particular, the set $[0,\infty ] \setminus {{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(d)$ is uncountable.

As an explicit example, we compute ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}(2)$ and ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(2)$ (Proposition 4.2) as well as ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(3)$ (Proposition 4.3). The case of non-tame 3-manifolds seems to be fairly tricky.

Question 1.3

What is ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}(3)$ ?

As ${{\,\mathrm{SV}\,}}(4) \subset {{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(4)$, we know that ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(4)$ contains arbitrarily small transcendental numbers [11].

From a geometric point of view, the so-called Lipschitz simplicial volume is more suitable for Riemannian non-compact manifolds than the locally finite simplicial volume. It is therefore natural to ask the following:

Question 1.4

Do Theorem A and Theorem B also hold for the Lipschitz simplicial volume of oriented connected open Riemannian manifolds?

1.1 Organisation of this article

Section 2 contains the proof of Theorem A. The proof of Theorem B is given in Sect. 3. The low-dimensional case is treated in Sect. 4.

2 Proof of Theorem A

Let $d \in {\mathbb {N}}_{\ge 4}$ and let $\alpha \in [0,\infty ]$. Because ${{\,\mathrm{SV}\,}}(d)$ is dense in ${\mathbb {R}}_{\ge 0}$ (Theorem 1.2), there exists a sequence $(\alpha _n)_{n \in {\mathbb {N}}}$ in ${{\,\mathrm{SV}\,}}(d)$ with $\sum _{n=0}^\infty \alpha _n = \alpha$.

2.1 Construction

We first describe the construction of a corresponding oriented connected open manifold M: For each $n \in {\mathbb {N}}$, we choose an oriented closed connected d-manifold $M_n$ with $\Vert M_n \Vert = \alpha _n$. Moreover, for $n >0$, we set

$$\begin{aligned} W_n := M_n \setminus (B_{n,-}^\circ \sqcup B_{n,+}^\circ ),\end{aligned}$$

where $B_{n,-} = i_{n,-}(D^d)$ and $B_{n,+} = i_{n,+}(D^d)$ are two disjointly embedded closed d-balls in $M_n$. Similarly, we set $W_0 := M_0 \setminus B_{0,+}^\circ$. Furthermore, we choose an orientation-reversing homeomorphism $f_n :S^{d-1} \rightarrow S^{d-1}$. We then consider the infinite “linear” connected sum manifold (Fig. 1)

$$\begin{aligned} M&:= M_0 \mathbin {\#}M_1 \mathbin {\#}M_2 \mathbin {\#}\dots \\&= (W_0 \sqcup W_1 \sqcup W_n \sqcup \dots )/\!\sim , \end{aligned}$$

where $\sim$ is the equivalence relation generated by

$$\begin{aligned} i_{n+1,-}(x) \sim i_{n,+}\bigl (f_n(x)\bigr ) \end{aligned}$$

for all $n \in {\mathbb {N}}$ and all $x \in S^{d-1} \subset D^d$; we denote the induced inclusion $W_n \rightarrow M$ by $i_n$. By construction, M is connected and inherits an orientation from the $M_n$.

Fig. 1

The construction of M for the proof of Theorem A

2.2 Computation of the simplicial volume

We will now verify that $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} =\alpha$:

Claim 2.1

We have $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} \le \alpha$.

Proof

The proof is a straightforward adaption of the chain-level proof of sub-additivity of simplicial volume with respect to amenable glueings.

In particular, we will use the uniform boundary condition [19] and the equivalence theorem [2, 9]:

• UBC The chain complex $C_*(S^{d-1};{\mathbb {R}})$ satisfies $(d-1)$-UBC, i.e., there is a constant K such that: For each $c \in {{\,\mathrm{im}\,}}\partial _d \subset C_{d-1}(S^{d-1};{\mathbb {R}})$, there exists a chain $b \in C_d(S^{d-1};{\mathbb {R}})$ with

  $$\begin{aligned} \partial _d b = c \quad \text {and}\quad |b|_1 \le K \cdot |c|_1. \end{aligned}$$

• EQT Let N be an oriented closed connected d-manifold, let $B_1, \dots , B_k$ be disjointly embedded d-balls in N, and let $W := N \setminus (B_1^\circ \cup \dots , \cup B_k^\circ )$. Moreover, let $\epsilon \in {\mathbb {R}}_{>0}$. Then

  $$\begin{aligned} \Vert N\Vert = \inf \bigl \{ |z|_1 \bigm | z \in Z(W;{\mathbb {R}}),\ |\partial _d z|_1 \le \epsilon \bigr \}, \end{aligned}$$

  where $Z(W;{\mathbb {R}}) \subset C_d(W;{\mathbb {R}})$ denotes the set of all relative fundamental cycles of W.

Let $\epsilon \in {\mathbb {R}}_{>0}$. By EQT, for each $n \in {\mathbb {N}}$, there exists a relative fundamental cycle $z_n \in Z(W_n;{\mathbb {R}})$ with

$$\begin{aligned} |z_n|_1 \le \alpha _n + \frac{1}{2^n}\cdot \epsilon \quad \text {and}\quad |\partial _d z_n|_1 \le \frac{1}{2^n} \cdot \epsilon . \end{aligned}$$

We now use UBC to construct a locally finite fundamental cycle of M out of these relative cycles: For $n \in {\mathbb {N}}$, the boundary parts $C_{d-1}(i_n;{\mathbb {R}})(\partial _d z_n|_{B_{n,+}})$ and $-C_{d-1}(i_{n+1};{\mathbb {R}})(\partial _d z_{n+1}|_{B_{n+1},-})$ are fundamental cycles of the sphere $S^{d-1}$ (embedded via $i_n \circ i_{n,+}$ and $i_{n+1} \circ i_{n+1,-}$ into M, which implicitly uses the orientation-reversing homeomorphism $f_n$). By UBC, there exists a chain $b_n \in C_d(S^{d-1};{\mathbb {R}})$ with

$$\begin{aligned} \partial _d C_d(i_n \circ i_{n,+};{\mathbb {R}}) (b_n)&= \; C_{d-1}(i_n ;{\mathbb {R}})(\partial _d z_n|_{B_{n,+}})\\&\quad + \; C_{d-1}(i_{n+1};{\mathbb {R}}) (\partial _d z_{n+1}|_{B_{n+1,-}}) \end{aligned}$$

and

$$\begin{aligned} |b_n|_1 \le K \cdot \Bigl (\frac{1}{2^n} + \frac{1}{2^{n+1}}\Bigr ) \cdot \epsilon \le K \cdot \frac{1}{2^{n-1}} \cdot \epsilon . \end{aligned}$$

A straightforward computation shows that

$$\begin{aligned} c := \sum _{n=0}^\infty C_d(i_n;{\mathbb {R}})\bigl (z_n - C_d(i_{n,+};{\mathbb {R}})(b_n)\bigr ) \end{aligned}$$

is a locally finite d-cycle on M. Moreover, the local contribution on $W_0$ shows that c is a locally finite fundamental cycle of M. By construction,

$$\begin{aligned} |c|_1&\le \sum _{n=0}^\infty \bigl (|z_n|_1 + |b_n|_1\bigr ) \\&\le \sum _{n=0}^\infty \Bigl ( \alpha _n + \frac{1}{2^n} \cdot \epsilon + K \cdot \frac{1}{2^{n-1}} \cdot \epsilon \Bigr ) \le \sum _{n=0}^\infty \alpha _n + (2 + 4 \cdot K) \cdot \epsilon \\&= \alpha + (2 + 4 \cdot K) \cdot \epsilon . \end{aligned}$$

Thus, taking $\epsilon \rightarrow 0$, we obtain $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}}\le \alpha$. $\square$

Claim 2.2

We have $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} \ge \alpha$.

Proof

Without loss of generality we may assume that $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}}$ is finite. Let $c \in C^{{{\,\mathrm{lf}\,}}}_d(M;{\mathbb {R}})$ be a locally finite fundamental cycle of M with $|c|_1 < \infty$. For $n \in {\mathbb {N}}$, we consider the subchain $c_n := c|_{W_{(n)}}$ of c, consisting of all simplices whose images touch $W_{(n)} := \bigcup _{k=0}^n i_k(W_k) \subset M$. Because c is locally finite, each $c_n$ is a finite singular chain and $(|c_n|_1)_{n\in {\mathbb {N}}}$ is a monotonically increasing sequence with limit $|c|_1$.

Let $\epsilon \in {\mathbb {R}}_{>0}$. Then there is an $n \in {\mathbb {N}}_{>0}$ that satisfies $|c-c_n|_1 \le \epsilon$ and $\alpha - \sum _{k=0}^n \alpha _k \le \epsilon$. Let

$$\begin{aligned} p :M \rightarrow W_{(n)}/i_n(B_{n,+}) =: W \end{aligned}$$

be the map that collapses everything beyond stage $n+1$ to a single point x. Then $z := C_d(p;{\mathbb {R}})(c_n) \in C_d(W,\{x\};{\mathbb {R}})$ is a relative cycle and

$$\begin{aligned} |\partial _d z|_1 \le |\partial _d c_n|_1 \le |\partial _d (c-c_n)|_1 \le (d+1) \cdot |c- c_n|_1 \le (d+1) \cdot \epsilon . \end{aligned}$$

Because $d > 1$, there exists a chain $b \in C_{d}(\{x\};{\mathbb {R}})$ with

$$\begin{aligned} \partial _{d} b = \partial _d z \quad \text {and}\quad |b|_1 \le |\partial _d z| \le (d+1) \cdot \epsilon . \end{aligned}$$

Then

$$\begin{aligned} {{\overline{z}}} := z - b \in C_d(W;{\mathbb {R}}) \end{aligned}$$

is a cycle on W; because z and ${{\overline{z}}}$ have the same local contribution on $W_0$, the cycle z is a fundamental cycle of the manifold

$$\begin{aligned} W \cong M_0 \mathbin {\#}\dots \mathbin {\#}M_n. \end{aligned}$$

As $d > 2$, the construction of our chains and additivity of simplicial volume under connected sums [2, 9] show that

$$\begin{aligned} |c|_1&\ge |c_n|_1 \ge |z|_1 \ge |{{\overline{z}}}|_1 - |b|_1 \\&\ge \Vert W\Vert - (d+1) \cdot \epsilon = \sum _{k=0}^n \Vert M_k\Vert - (d+1) \cdot \epsilon \\&\ge \alpha - (d+2) \cdot \epsilon . \end{aligned}$$

Thus, taking $\epsilon \rightarrow 0$, we obtain $|c|_1 \ge \alpha$; hence, $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} \ge \alpha$. $\square$

This completes the proof of Theorem A.

Remark 2.3

(adding geometric structures) In fact, this argument can also be performed smoothly: The constructions leading to Theorem 1.2 can be carried out in the smooth setting. Therefore, we can choose the $(M_n)_{n \in {\mathbb {N}}}$ to be smooth and equip M with a corresponding smooth structure. Moreover, we can endow these smooth pieces with Riemannian metrics. Scaling these Riemannian metrics appropriately shows that we can turn M into a Riemannian manifold of finite volume.

3 Proof of Theorem B

In this section, we prove Theorem B, i.e., that the set of simplicial volumes of tame manifolds is countable.

Definition 3.1

A manifold M without boundary is tame if there exists a compact connected manifold W with boundary such that M is homeormorphic to $W^\circ := W \setminus \partial W$.

As in the closed case, our proof is based on a counting argument:

Proposition 3.2

There are only countably many proper homotopy types of tame manifolds.

As we could not find a proof of this statement in the literature, we will give a complete proof in Sect. 3.1 below. Theorem B is a direct consequence of Proposition 3.2:

Proof of Theorem B

The simplicial volume $\Vert \cdot \Vert ^{{{\,\mathrm{lf}\,}}}$ is invariant under proper homotopy equivalence (this can be shown as in the compact case). Therefore, the countability of ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}(d)$ follows from the countability of the set of proper homotopy types of tame d-manifolds (Proposition 3.2).$\square$

Remark 3.3

Let $d \in {\mathbb {N}}_{\ge 3}$. Then $\infty \in {{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(d)$: Let N be an oriented closed connected hyperbolic $(d-1)$-manifold and let $M := N \times {\mathbb {R}}$. Then M is tame (as interior of $N \times [0,1]$) and $\Vert N\Vert > 0$ [9, Section 0.3] [23, Theorem 6.2]. Hence, by the finiteness criterion [9, p. 17] [14, Theorem 6.4], we obtain that $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} = \infty$.

3.1 Counting tame manifolds

It remains to prove Proposition 3.2. We use the following observations:

Definition 3.4

(models of tame manifolds)

• A model of a tame manifold M is a finite CW-pair (X, A) (i.e., a finite CW-complex X with a finite subcomplex A) that is homotopy equivalent (as pairs of spaces) to $(W,\partial W)$, where W is a compact connected manifold with boundary whose interior is homeomorphic to M.

• Two models of tame manifolds are equivalent if they are homotopy equivalent as pairs of spaces.

Lemma 3.5

(existence of models) Let W be a compact connected manifold. Then there exists a finite CW-pair (X, A) such that $(W,\partial W)$ and (X, A) are homotopy equivalent pairs of spaces.

In particular: Every tame manifold admits a model.

Proof

It should be noted that we work with topological manifolds; hence, we cannot argue directly via triangulations. Of course, the main ingredient is the fact that every compact manifold is homotopy equivalent to a finite complex [13, 22].

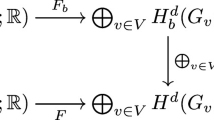
Hence, there exist finite CW-complexes A and Y with homotopy equivalences $f :A\rightarrow \partial W$ and $g :Y \rightarrow W$. Let $j := {{\overline{g}}} \circ i \circ f$, where $i :\partial W \hookrightarrow W$ is the inclusion and ${{\overline{g}}}$ is a homotopy inverse of g. By construction, the upper square in the diagram in Fig. 2 is homotopy commutative.

As next step, we replace $j :A \rightarrow Y$ by a homotopic map $j_c :A \rightarrow Y$ that is cellular (second square in Fig. 2).

The mapping cylinder Z of $j_c$ has a finite CW-structure (as $j_c$ is cellular) and the canonical map $p :Z \rightarrow Y$ allows to factor $j_c$ into an inclusion J of a subcomplex and the homotopy equivalence p (third square in Fig. 2).

We thus obtain a homotopy commutative square

where the vertical arrows are homotopy equivalences, the upper horizontal arrow is the inclusion, and the lower horizontal arrow is the inclusion of a subcomplex.

Using a homotopy between $i \circ f$ and $F \circ J$ and adding another cylinder to Z, we can replace Z by a finite CW-complex X (that still contains A as subcomplex) to obtain a strictly commutative diagram

whose vertical arrows are homotopy equivalences and whose horizontal arrows are inclusions.

Because the inclusions $\partial W \hookrightarrow W$ (as inclusion of the boundary of a compact topological manifold) and $A \hookrightarrow X$ (as inclusion of a subcomplex) are cofibrations, this already implies that the vertical arrows form a homotopy equivalence $(X,A) \rightarrow (W,\partial W)$ of pairs [18, Chapter 6.5]. $\square$

Fig. 2

Finding a model

Lemma 3.6

(equivalence of models) If M and N are tame manifolds with equivalent models, then M and N are properly homotopy equivalent.

Proof

As M and N admit equivalent models, there exist compact connected manifolds W and V with boundary such that $M \cong W^\circ$ and $N \cong V^\circ$ and such that the pairs $(W,\partial W)$ and $(V,\partial V)$ are homotopy equivalent (by transitivity of homotopy equivalence of pairs of spaces). Let $(f, f_\partial ) :(W,\partial W) \rightarrow (V,\partial V)$ and $(g,g_\partial ) :(V,\partial V) \rightarrow (W,\partial W)$ be mutually homotopy inverse homotopy equivalences of pairs.

By the topological collar theorem [5, 6], we have homeomorphisms

$$\begin{aligned} M&\cong W \cup _{\partial W} \bigl ( \partial W \times [0,\infty ) \bigr ) \\ N&\cong V \cup _{\partial V} \bigl ( \partial V \times [0,\infty ) \bigr ), \end{aligned}$$

where the glueing occurs via the canonical inclusions $\partial W \hookrightarrow \partial W \times [0,\infty )$ and $\partial V \hookrightarrow \partial V \times [0,\infty )$ at parameter 0.

Then the maps f and $f_\partial \times {{\,\mathrm{id}\,}}_{[0,\infty )}$ glue to a well-defined proper continuous map $F :M \rightarrow N$ and the maps g and $g_\partial \times {{\,\mathrm{id}\,}}_{[0,\infty )}$ glue to a well-defined proper continuous map $G :N \rightarrow M$.

Moreover, the homotopy of pairs between $(f \circ g, f_\partial \circ g_\partial )$ and $({{\,\mathrm{id}\,}}_V,{{\,\mathrm{id}\,}}_{\partial V})$ glues into a proper homotopy between $F \circ G$ and ${{\,\mathrm{id}\,}}_M$. In the same way, there is a proper homotopy between $G \circ F$ and ${{\,\mathrm{id}\,}}_N$. Hence, the spaces M and N are properly homotopy equivalent. $\square$

Lemma 3.7

(countability of models) There exist only countably many equivalence classes of models.

Proof

There are only countably many homotopy types of finite CW-complexes (because every finite CW-complex is homotopy equivalent to a finite simplicial complex). Moreover, every finite CW-complex has only finitely many subcomplexes. Therefore, there are only countably many homotopy types (of pairs of spaces) of finite CW-pairs. $\square$

Proof of Proposition 3.2

We only need to combine Lemma 3.5, Lemma 3.6, and Lemma 3.7. $\square$

4 Low dimensions

4.1 Dimension 2

We now compute the set of simplicial volumes of surfaces. We first consider the tame case:

Example 4.1

(tame surfaces) Let W be an oriented compact connected surface with $g\in {\mathbb {N}}$ handles and $b \in {\mathbb {N}}$ boundary components. Then the proportionality principle for simplicial volume of hyperbolic manifolds [9, p. 11] (a thorough exposition is given, for instance, by Fujiwara and Manning [7, Appendix A]) gives

$$\begin{aligned} \Vert W^\circ \Vert ^{{{\,\mathrm{lf}\,}}} = {\left\{ \begin{array}{ll} 4 \cdot (g-1) + 2 \cdot b &{} \hbox { if }\ g>0 \\ 2 \cdot b - 4 &{} \hbox {if}\, g=0\, \hbox {and}\, b>1 \\ 0 &{} \text { if }g=0 \text { and }b \in \{0,1\}. \end{array}\right. } \end{aligned}$$

Proposition 4.2

We have ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}(2) = 2 \cdot {\mathbb {N}}\cup \{\infty \}$ and ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(2) = 2 \cdot {\mathbb {N}}$.

Proof

We first prove $2 \cdot {\mathbb {N}}\subset {{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(2) \subset {{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}(2)$ and $\infty \in {{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}(2)$, i.e., that all the given values may be realised: In view of Example 4.1, all even numbers occur as simplicial volume of some (possibly open) tame surface.

Let

$$\begin{aligned} M := T^2 \mathbin {\#}T^2 \mathbin {\#}T^2 \mathbin {\#}\dots \end{aligned}$$

be an infinite “linear” connected sum of tori $T^2$. Collapsing M to the first $g \in {\mathbb {N}}$ summands and an argument as in the proof of Claim 2.2 shows that

$$\begin{aligned} \Vert M \Vert ^{{{\,\mathrm{lf}\,}}} \ge \Vert \Sigma _g \Vert = 4 \cdot g - 4 \end{aligned}$$

for all $g \in {\mathbb {N}}_{\ge 1}$. Hence, $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} = \infty$.

It remains to show that ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}(2) \subset 2 \cdot {\mathbb {N}}\cup \{\infty \}$: Let M be an oriented connected (topological, separable, Hausdorff) 2-manifold without boundary. Then M admits a smooth structure [20] and whence a proper smooth map $p :M \rightarrow {\mathbb {R}}$. Using suitable regular values of p, we can thus write M as an ascending union

$$\begin{aligned} M = \bigcup _{n\in {\mathbb {N}}} M_n \end{aligned}$$

of oriented connected compact submanifolds (possibly with boundary) $M_n$ that are nested via $M_0 \subset M_1 \subset \dots$. Then one of the following cases occurs:

• 1. There exists an $N \in {\mathbb {N}}$ such that for all $n \in {\mathbb {N}}_{\ge N}$ the inclusion $M_n \hookrightarrow M_{n+1}$ is a homotopy equivalence.

• 2. For each $N \in {\mathbb {N}}$ there exists an $n \in {\mathbb {N}}_{\ge N}$ such that the inclusion $M_n \hookrightarrow M_{n+1}$ is not a homotopy equivalence.

In the first case, the classification of compact surfaces with boundary shows that M is tame. Hence $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} \in 2 \cdot {\mathbb {N}}$ (Example 4.1).

In the second case, the manifold M is not tame (which can, e.g., be derived from the classification of compact surfaces with boundary). We show that $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} = \infty$. To this end. we distinguish two cases:

• a. The sequence $(h(M_n))_{n \in {\mathbb {N}}}$ is unbounded, where $h(\;\cdot \;)$ denotes the number of handles of the surface.

• b. The sequence $(h(M_n))_{n \in {\mathbb {N}}}$ is bounded.

In the unbounded case, a collapsing argument (similar to the argument for $T^2 \mathbin {\#}T^2 \mathbin {\#}\dots$ and Claim 2.2) shows that $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} = \infty$.

We claim that also in the bounded case we have $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} = \infty$: Shifting the sequence in such a way that all handles are collected in $M_0$, we may assume without loss of generality that the sequence $(h(M_n))_{n \in {\mathbb {N}}}$ is constant. Thus, for each $n \in {\mathbb {N}}$, the surface $M_{n+1}$ is obtained from $M_n$ by adding a finite disjoint union of disks and of spheres with finitely many (at least two) disks removed; we can reorganise this sequence in such a way that no disks are added. Hence, we may assume that $M_{n}$ is a retract of $M_{n+1}$ for each $n \in {\mathbb {N}}$. Furthermore, because we are in case 2, the classification of compact surfaces shows (with the help of Example 4.1) that

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert M_n\Vert = \infty . \end{aligned}$$

Let $c \in C^{{{\,\mathrm{lf}\,}}}_2(M;{\mathbb {R}})$ be a locally finite fundamental cycle of M and let $n\in {\mathbb {N}}$. Because c is locally finite, there is a $k \in {\mathbb {N}}$ such that $c|_{M_n}$ is supported on $M_{n+k}$; the restriction $c|_{M_n}$ consists of all summands of c whose supports intersect with $M_n$. Because $M_n$ is a retract of $M_{n+k}$, we obtain from $c|_{M_n}$ a relative fundamental cycle $c_n$ of $M_n$ by pushing the chain $c|_{M_n}$ to $M_n$ via a retraction $M_{n+k} \rightarrow M_n$. Therefore,

$$\begin{aligned} |c|_1 \ge |c|_{M_n}|_1 \ge |c_n|_1 \ge \Vert M_n\Vert . \end{aligned}$$

Taking $n \rightarrow \infty$ shows that $|c|_1 = \infty$. Taking the infimum over all locally finite fundamental cycles c of M proves that $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} = \infty$.

Moreover, Example 4.1 shows that $\infty \not \in {{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(2)$. $\square$

4.2 Dimension 3

The general case of non-compact 3-manifolds seems to be rather involved (as the structure of non-compact 3-manifolds can get fairly complicated). We can at least deal with the tame case:

Proposition 4.3

We have ${{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(3) = {{\,\mathrm{SV}\,}}(3) \cup \{\infty \}$.

Proof

Clearly, ${{\,\mathrm{SV}\,}}(3) \subset {{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(3)$ and $\infty \in {{\,\mathrm{SV}\,}}^{{{\,\mathrm{lf}\,}}}_{{{\,\mathrm{tame}\,}}}(3)$ (Remark 3.3).

Conversely, let W be an oriented compact connected 3-manifold and let $M := W^\circ$. We distinguish the following cases:

• If at least one of the boundary components of W has genus at least 2, then the finiteness criterion [9, p. 17] [14, Theorem 6.4] shows that $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} = \infty$.

• If the boundary of W consists only of spheres and tori, then we proceed as follows: In a first step, we fill in all spherical boundary components of W by 3-balls and thus obtain an oriented compact connected 3-manifold V all of whose boundary components are tori. In view of considerations on tame manifolds with amenable boundary [12] and glueing results for bounded cohomology [9] [2], we obtain that

  $$\begin{aligned} \Vert M \Vert ^{{{\,\mathrm{lf}\,}}} = \Vert W \Vert = \Vert V\Vert . \end{aligned}$$

  By Kneser’s prime decomposition theorem [1, Theorem 1.2.1] and the additivity of (relative) simplicial volume with respect to connected sums [2, 9] in dimension 3, we may assume that V is prime (i.e., admits no non-trivial decomposition as a connected sum). Moreover, because $\Vert S^1 \times S^2\Vert = 0$, we may even assume that V is irreducible [1, p. 3].

  By geometrisation [1, Theorem 1.7.6], then V admits a decomposition along finitely many incompressible tori into Seifert fibred manifolds (which have trivial simplicial volume [23, Corollary 6.5.3]) and hyperbolic pieces $V_1, \dots , V_k$. As the tori are incompressible, we can now again apply additivity [2, 9] to conclude that

  $$\begin{aligned} \Vert V\Vert = \sum _{j=1}^k \Vert V_j\Vert . \end{aligned}$$

  Let $j \in \{1,\dots , k\}$. Then the boundary components of $V_j$ are $\pi _1$-injective tori (as the interior of $V_j$ admits a complete hyperbolic metric of finite volume) [4, Proposition D.3.18]. Let S be a Seifert 3-manifold whose boundary is a $\pi _1$-injective torus (e.g., the knot complement of a non-trivial torus knot [21, Theorem 2] [17, Lemma 4.4]). Filling each boundary component of $V_j$ with a copy of S results in an oriented closed connected 3-manifold $N_j$, which satisfies (again, by additivity)

  $$\begin{aligned} \Vert N_j\Vert = \Vert V_j\Vert + 0 = \Vert V_j\Vert . \end{aligned}$$

  Therefore, the oriented closed connected 3-manifold $N := N_1 \mathbin {\#}\dots \mathbin {\#}N_k$ satisfies

  $$\begin{aligned} \Vert N\Vert = \sum _{j=1}^k \Vert N_j\Vert = \sum _{j=1}^k \Vert V_j\Vert = \Vert V\Vert . \end{aligned}$$

  In particular, $\Vert M \Vert ^{{{\,\mathrm{lf}\,}}} = \Vert V\Vert = \Vert N\Vert \in {{\,\mathrm{SV}\,}}(3)$. $\square$