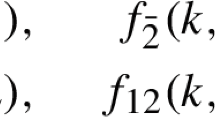Abstract
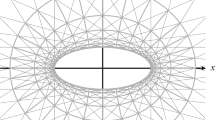
We present a procedure which allows one to integrate explicitly the class of checkerboard IC-nets which has recently been introduced as a generalisation of incircular (IC) nets. The latter class of privileged congruences of lines in the plane is known to admit a great variety of geometric properties which are also present in the case of checkerboard IC-nets. The parametrisation obtained in this manner is reminiscent of that associated with elliptic billiards. Connections with discrete confocal coordinate systems and the fundamental QRT maps of integrable systems theory are made. The formalism developed in this paper is based on the existence of underlying pencils of conics and quadrics which is exploited in a Laguerre geometric setting.
















Similar content being viewed by others
References
Akopyan, A., Bobenko, A.I.: Incircular nets and confocal conics. Trans. AMS 370(4), 2825–2854 (2018)
Blaschke, W.: Untersuchungen über die Geometrie der Speere in der Euklidischen Ebene, Separatdruck aus “Monatshefte f. Mathematik u. Physik”, XXI, Hamburg (1910)
Blaschke, W., Thomsen, G.: Vorlesungen über Differentialgeometrie und Geometrische Grundlagen von Einsteins Relativitätstheorie. III. Differentialgeometrie der Kreise und Kugeln. Springer, Berlin (1929)
Bobenko, A.I., Schief, W.K., Suris, Y.B., Techter, J.: On a discretization of confocal quadrics. I. An integrable systems approach. J. Integrable Syst. 1, xyw005 (2016). (34 pp)
Bobenko, A.I., Schief, W.K., Suris, Y.B., Techter, J.: On a discretization of confocal quadrics. II. A geometric approach to general parametrizations. Int. Math. Res. Notices rny279 (2018). https://doi.org/10.1093/imrn/rny279
Bobenko, A.I., Suris, Y.B.: Discrete differential geometry. Integrable structure. In: Graduate Studies in Mathematics 98, (2008). Providence, AMS
Böhm, W.: Verwandte Sätze über Kreisvierseitnetze. Arch. Math. (Basel) 21, 326–330 (1970)
Darboux, G.: Leçons sur la Théorie Générale des surfaces et les applications Géométriques du Calcul Infinitésimal, vol. 2,3. Gauthier-Villars, Paris (1887)
Darboux, G.: Principes de Géométrie Analytique. Gauthier-Villars, Paris (1917)
Dragović, V., Radnović, M.: Poncelet Porisms and Beyond Integrable Billiards, Hyperelliptic Jacobians and Pencils of Quadrics, Frontiers in Mathematics. Birkhäuser, Basel (2011)
Iatrou, A., Roberts, J.A.G.: Integrable mappings of the plane preserving biquadratic invariant curves. J. Phys. A Math. Gen. 34, 6617–6636 (2001)
Izmestiev, I., Tabachnikov, S.: Ivory’s theorem revisited. J. Integr. Syst. 2, xyx006 (2017)
Levi, M., Tabachnikov, S.: The Poncelet grid and billiards in ellipses. Am. Math. Mon. 114, 895–908 (2007)
Levy, H.: Projective and Related Geometries. Macmillan, New York (1964)
NIST Digital Library of Mathematical Functions (online at dlmf.nist.gov), National Institute of Standards and Technology, U.S. Department of Commerce (2010–2018)
Pottmann, H., Grohs, P., Baschitz, B.: Edge offset meshes in Laguerre geometry. Adv. Comput. Math. 33(1), 45–73 (2010)
Quispel, G.R.W., Roberts, J.A.G., Thompson, C.J.: Integrable mappings and soliton equations II. Phys. D 34, 183–192 (1989)
Ramani, A., Grammaticos, B., Willox, R.: Generalized QRT mappings with periodic coefficients. Nonlinearity 24, 113–126 (2011)
Roberts, J.A.G., Jogia, D.: Birational maps that send biquadratic curves to biquadratic curves. J. Phys. A Math. Theor. 48, 08FT02 (2015)
Schwartz, R.E.: The Poncelet grid. Adv. Geom. 7, 157–175 (2007)
Skopenkov, M., Pottmann, H., Grohs, P.: Ruled Laguerre minimal surfaces. Math. Z. 272, 245–274 (2012)
Acknowledgements
We are indebted to Yuri Suris for insightful comments and discussions. This research was supported by the DFG Collaborative Research Center TRR 109 “Discretization in Geometry and Dynamics”. W.K.S. was also supported by the Australian Research Council (DP1401000851).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Laguerre geometry
Appendix: Laguerre geometry
Here, we present the basic facts about Laguerre geometry, focussing on the Blaschke cylinder model employed in this paper for studying checkerboard IC-nets. We begin with the more fundamental Lie sphere geometry. Lie sphere geometry in the plane is the geometry of oriented circles and lines. These are described as elements of the Lie quadric
Let \(e_1,e_2,e_3,e_4,e_5\) be an orthonormal basis with signature \((+++--)\). For our purposes, another basis \(e_1, e_2, e_5, e_\infty , e_0\) defined by
turns out to be more convenient. Elements of \(\mathscr {L}\) with non-vanishing \(e_0\)-component are identified with oriented circles \(|{\varvec{x}}-{\varvec{c}}|^2=r^2\), centred at \({\varvec{c}}\in \mathbb {R}^2\) and of radius \(r\in \mathbb {R}\):
Points are circles of radius \(r=0\), and oriented lines \(({\varvec{v}},{\varvec{x}})_{\mathbb {R}^2}=d\) are elements of \(\mathscr {L}\) with vanishing \(e_0\)-component:
The incidence \(<p,s>=0\) is the condition
of oriented contact of a circle and a line.
The Lie sphere transformation group \(\textit{PO}(3,2)\) acting on \(P(\mathbb {R}^{3,2})\) preserves the Lie quadric \(\mathscr {L}\) and maps oriented circles and lines to oriented circles and lines, preserving oriented contact. Its subgroup of Laguerre transformations preserves the set of straight lines or, equivalently, the hyperplane
Direct computation shows that the elements of \(\textit{PO}(3,2)\) preserving the hyperplane \(\mathsf P\) are of the form
in the basis \(e_1,e_2,e_5,e_\infty ,e_0\), where
In order to pass to the Blaschke cylinder model of Laguerre geometry, we confine ourselves to the subspace \({\mathscr {P}}=\mathrm{span}\{e_1,e_2,e_5,e_\infty \}\). Elements of this space can be identified with straight lines, described (projectively) by
as points of the Blaschke cylinder
Identification with (43) is made via the normalisation of the \(e_0\)-component: \({\varvec{v}}=\tilde{{\varvec{v}}}/\tilde{s}\), \(d=\tilde{d}/\tilde{s}\). It is noted that the symmetry with the description of circles (42) in Lie sphere geometry is no longer present in the Blaschke cylinder model, and oriented circles are described as the sets of all straight lines in oriented contact, i.e., the sets of lines satisfying the condition (44), that is
Furthermore, Laguerre transformations restricted to the subspace of lines \({\mathsf P}=\mathrm{span}\{e_1,e_2,e_5,e_\infty \}\) are of the form
Theorem 12
The group of Laguerre transformations in the Blaschke (projective) cylinder model (in the basis \(e_1,e_2,e_5,e_\infty \)) is represented by matrices of the form (46), where \(B\in O(2,1),\, b\in \mathbb {R}^{2,1},\, \lambda \in \mathbb {R}\). These transformations preserve the Blaschke cylinder (45).
We conclude by observing that Euclidean motions
are particular Laguerre transformations, the corresponding matrix of which is given by (46) with
and \(\lambda =1\).
Rights and permissions
About this article
Cite this article
Bobenko, A.I., Schief, W.K. & Techter, J. Checkerboard incircular nets: Laguerre geometry and parametrisation. Geom Dedicata 204, 97–129 (2020). https://doi.org/10.1007/s10711-019-00449-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10711-019-00449-x
Keywords
- Discrete differential geometry
- Confocal conics
- Laguerre geometry
- Pencils of quadrics
- Discrete integrable systems