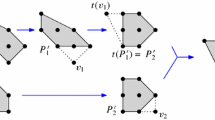
Abstract
We calculate the area of the smallest triangle and the area of the smallest virtual triangle for many known lattice surfaces. We show that our list of the lattice surfaces for which the area of the smallest virtual triangle greater than \(1\over 20\) is complete. In particular, this means that there are no new lattice surfaces for which the area of the smallest virtual triangle is greater than .05. Our method follows an algorithm described by Smillie and Weiss and improves on it in certain respects.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bainbridge, M., Habegger, P., Moeller, M.: Teichmüeller curves in genus three and just likely intersections in \({G}_m^n\times {G}_a^n\). arXiv preprint arXiv:1410.6835 (2014)
Bainbridge, M., Möller, M.: The Deligne–Mumford compactification of the real multiplication locus and Teichmüller curves in genus 3. Acta Math. 208(1), 1–92 (2012)
Bouw, I.I., Möller, M.: Teichmüller curves, triangle groups, and Lyapunov exponents. Ann. Math. 172(2), 139–185 (2010)
Calta, K.: Veech surfaces and complete periodicity in genus two. J. Am. Math. Soc. 17(4), 871–908 (2004)
Delecroix, V.: Flatsurf package of sagemath. http://www.labri.fr/perso/vdelecro/flatsurf.html
Eskin, A., Mirzakhani, M., Mohammadi, A.: Isolation, equidistribution, and orbit closures for the \({SL}(2, {\mathbb{R}})\) action on Moduli space. Ann. Math. 182(2), 673–721 (2015)
Hooper, W.P.: Grid graphs and lattice surfaces. Int. Math. Res. Not. 2013(12), 2657–2698 (2013)
Kenyon, R., Smillie, J.: Billiards on rational-angled triangles. Comment. Math. Helv. 75(1), 65–108 (2000)
Lanneau, E., Nguyen, D.M.: Teichmüller curves generated by Weierstrass Prym eigenforms in genus 3 and genus 4. J. Topol. 7(2), 475–522 (2014)
Lanneau, E., Nguyen, D.M., Wright, A.: Finiteness of Teichmüller curves in non-arithmetic rank 1 orbit closures. arXiv preprint arXiv:1504.03742 (2015)
Leininger, C.J.: On groups generated by two positive multi-twists: Teichmüller curves and Lehmers number. Geom. Topol. 8(3), 1301–1359 (2004)
Matheus, C., Wright, A.: Hodge-Teichmüller planes and finiteness results for Teichmüller curves. Duke Math. J. 164(6), 1041–1077 (2015)
McMullen, C.T.: Teichmüller curves in genus two: discriminant and spin. Math. Ann. 333(1), 87–130 (2005)
McMullen, C.T., et al.: Prym varieties and teichmüller curves. Duke Math. J. 133(3), 569–590 (2006)
Smillie, J., Weiss, B.: Minimal sets for flows on moduli space. Isr. J. Math. 142(1), 249–260 (2004)
Smillie, J., Weiss, B.: Characterizations of lattice surfaces. Invent. Math. 180(3), 535–557 (2010)
Thurston, W.P., et al.: On the geometry and dynamics of diffeomorphisms of surfaces. Bull. New. Ser. Am. Math. Soc. 19(2), 417–431 (1988)
Veech, W.A.: Teichmüller curves in moduli space, Eisenstein series and an application to triangular billiards. Invent. Math. 97(3), 553–583 (1989)
Vorobets, Y.B.: Planar structures and billiards in rational polygons: the Veech alternative. Russ. Math. Surv. 51(5), 779–817 (1996)
Wright, A.: Schwarz triangle mappings and Teichmüller curves: abelian square-tiled surfaces. J. Mod. Dyn. 6(3), 405–426 (2012)
Wright, A.: Translation surfaces and their orbit closures: An introduction for a broad audience. arXiv preprint arXiv:1411.1827 (2014)
Zhong, Y.: On the areas of the minimal triangles in Veech surfaces (in preparation)
Acknowledgments
The author thanks his thesis advisor John Smillie for suggesting the problem and for many helpful conversations, and Alex Wright and Anja Randecker for many helpful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wu, C. Lattice surfaces and smallest triangles. Geom Dedicata 187, 107–121 (2017). https://doi.org/10.1007/s10711-016-0191-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10711-016-0191-z