1 Introduction

Expansive clays are subject to movements due to shrinkage from natural evaporation, water absorption by the root system of vegetation, and swelling caused by water ingress (Richards et al. 1983). The water potential must be lower in plants (e.g. more negative) than in the soil to allow water to be extracted by the roots and transported to the leaves for transpiration via the water-conducting xylem tissues. The water distribution in the soil primarily depends on the plants' root distribution if the soil water content is well below the field capacity. The amount of moisture extracted by vegetation varies greatly depending on seasonality, with functional transpiration mainly occurring in the growing season (Holtz 1983). The seasonal volume change of desiccated clays increases the severity of shrinkage; the scenario can be further exacerbated by the effect of tree root desiccation. The substantial soil movements can cause lesions in the overlying footing system and crack in the masonry walls (Li and Cameron 2002).

Studies have been conducted to investigate the influence of vegetation on soil desiccation. Coleman (1965) observed a significant seasonal variation in soil water content at 1 m below the ground surface covered by grasses. Richards et al. (1983) showed that soil suction is higher in close proximity to trees than in an open field with no trees, and gum trees can lead to significant soil desiccation than pine trees of a similar size. Jameson (1986) found that soil moisture content close to trees is about 5% less than soils most distant away from trees, while soil suction in the vicinity of trees is 0.2–0.3 pF higher than the value without the presence of trees. Blight (2005) found that the lateral influence of poplar trees and bushes on soil moisture conditions was 7.5 m and 4 m, respectively. Most recently, Sun et al. (2021) monitored soil movements close to a 14.5 m tall spotted gum in the spring and summer months and concluded that soil near the dripline suffered the greatest shrinkage settlement compared to soil farther away from the tree.

In Australia, domestic dwellings constructed in the early 1990s were subjected to greater risks of damage than recently built houses because those buildings were not designed to cater for tree root drying effects (Cameron and Beal 2011). Until the current edition of Australian Standard AS2870 (2011), the ‘tree proximity rule’ was introduced and assumed that the maximum design suction change occurs in close proximity to a tree, which may decrease as proximity is relaxed. The Standard stated that trees should be kept significantly distant away relative to their heights and density so that the trees were unlikely to impact the movement of the footing of a structure. For example, trees cause no influence on a footing constructed from a distance equal to the mature height (HT) of a tree in the case of a single tree. The distance extended to 1.5 HT for a group of 3 trees and 2 HT for a group of 4 trees and more. Unfortunately, the proximity rules do not take into account the information on tree species and water demand. On the other hand, the UK version of the ‘proximity rule’ published by the National House Building Council considered the minimum distances from trees to a building and water usage of various tree species, which provide guidance for designing buildings constructed on clay soils (NHBC 2021). The level of water usage of trees was ranked from low to high; however, published long-term water use data from field measurements for different tree species is scarce (Lawson and O’Callaghan 1995).

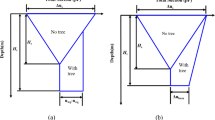
AS2870 (2011) introduced a method to categorize the site reactivity ranging from S site (slightly reactive) to E site (extremely reactive), based on the potential ground surface movement ys, which is relied on the design soil suction profile (Fig. 1) and is estimated by adding the movement of each soil layer within the depth of design suction change Hs, using Eq. 1. The extra potential soil surface movement due to tree root drying yt, is determined based on the tree-induced additional design suction changes and a deeper depth Ht, following Eq. 2. The triangular-shaped ‘normal’ soil suction change due to local climate conditions is illustrated in Fig. 1. The Standard assumes that the design soil suction change is the greatest (e.g. 1.2 pF) at the ground surface, which lessened progressively with depth until the Hs. The shaded area in Fig. 1 presents the tree-induced design soil suction change. The drying depth is extended from Hs to Ht, and the maximum suction change at Ht caused by the effect of tree root drying is indicated by Δubase. At the field site, Δubase can be determined from the differences between deep equilibrium suction ueq and wilting point soil suction uwp, which is the threshold beyond which tree roots cannot draw water from the soil.

$$y_{s} = \frac{1}{{{100}}}\mathop \sum \limits_{{\text{n = 1}}}^{N} \left( {I_{{{\text{pt}}}} \overline{\Delta u} h} \right)_{{\text{n}}}$$
(1)
$$y_{t} = \left[ {1 - \left( {\frac{{\frac{{D_{t} }}{HT} - 0.5}}{{\frac{{D_{i} }}{HT} - 0.5}}} \right)} \right]y_{t\max }$$
(2)

where Ipt is the instability index (%/pF or %/log (kPa)). It is a useful indicator of soil reactivity and is determined from the shrink-swell soil testing following AS1289.7.1.1 (2003);\(\overline{\Delta u}\) is the mean soil suction change for the soil layer (pF or log(kPa)); N and h are the number of layers within the Hs and the soil layer depth (mm), respectively; Dt is the distance of a tree to the building (m); Di is the influence distance of a tree (m); yt max is the tree-induced maximum potential soil surface movements (mm), and is estimated per the principle used to calculate the ys using Eq. 1.

Fig. 1
figure 1

The design suction change profile provided by the Standard

Full size image

2 Site Description

The most famous Australian native tree species, C. maculata, located in a nature reserve in Melbourne (37°53'S, 145°15'E), Australia, was chosen to study its influence on the ground surface movement. The tree height of 14.6 m and diameter at breast height (DBH) of 0.56 m were measured using a clinometer and a fiberglass tape, respectively. The site is located in Climate Zone 3 (i.e. temperate climate), with the yearly mean maximum temperature and minimum temperature of 19.7 °C and 9.6 °C, respectively (Li and Sun 2015; BOM 2022). Based on a 70-year weather record, the annual average rainfall is 858.5 mm and the annual average solar radiation is 14.6 MJ /m2. The site layout is presented in Fig. 2. A total of 28 galvanized steel survey pins were installed in the vicinity of the tree, with two rows of 8 pins spaced at 2.0 m located at the edge of the asphalt footpath on the south-west side, whereas another two rows of 6 pins are spaced at 2.6 m on the north-east side of the tree. A deep benchmark was located 6.5 m away from the tree.

Fig. 2
figure 2

Layout of the experimental site (not to scale)

Full size image

2.1 Benchmark Establishment

Since the nearest Lands Department Benchmark (LDBM) is located a few hundred meters away from the study site and was difficult to access, a deep survey datum was designed and established to provide a reliable reference point for conducting the level survey. Because the site is covered by expansive clays, it is essential that the benchmark be anchored below the moisture/suction active zone (e.g. Hs) to ensure it is free from soil movements. It was suggested by AS2870 (2011) that the depth of Hs for Melbourne is ranged from 1.8 to 2.3 m. The benchmark was installed 5.3 m below the ground surface. Little or no soil movement is expected to occur below this depth.

The details of the benchmark (BM) are depicted in Fig. 3. During installation, a 100 mm diameter borehole was drilled to the depth of 5.3 m using a hydraulic drilling rig at 6.5 m east of the tree. A 5.25 m long galvanized steel rod with a diameter of 25 mm was lowered to the bottom of the borehole, followed by pouring quick set pre-mixed concrete to a thickness of approximately 200 mm to allow the steel rod to be anchored. The concrete was cured overnight to provide good anchorage for the steel rod. A 5 m long, 50 mm diameter aluminum sleeve was placed over the steel rod to the point where it rested on the concrete anchor isolating the rod from soil movement. The pellet mixture of bentonite and concrete, minimizing the downward movement of water due to low permeability, was used to fill the annular space between the sleeve and the boring wall. The top of the steel rod formed the survey benchmark point. The top of the borehole was widened to allow a 300 mm long, 150 mm diameter PVC pipe to be installed at the top of the bore casing and capped with a cast iron locking cover to protect the benchmark from disturbance. The constructed benchmark was approximately 50 mm higher than the existing ground surface. A 30 mm thick concrete pad was built to surround the benchmark, and the surface was finished with a 10% slope to drain water away from the locking cover.

Fig. 3
figure 3

Details of the benchmark (BM)

Full size image

3 Site Investigation and Soil Testing

Two boreholes (BHs) were drilled at a distance away from the tree (BH1) in Feb 2017 and near the dripline (BH2) in Oct 2017. Groundwater was not encountered in any of the BHs during drilling. The location of the BHs in relation to the tree is presented in Fig. 2. Soil logging was performed following the BH drilling, and samples were collected at every 0.25 m and sealed in heavy-duty polythene plastic bags prior to transporting to the laboratory for suction and water content testing.

3.1 Soil Profile

The soil profile in BH 1 is described in Table 1. The soil included a fill of 0.25 m thick silty loam, underlain by a layer of intermediate-plasticity silty clay with a thickness of 2.55 m, becoming high-plasticity to the full depth of 3.3 m. Tree roots were found at depths from 0.25 to 1.50 m, with the diameter varying between 0.2 and 0.5 mm measured by a crack width gauge. The soil profile for BH 2 is similar to BH 1, with a deeper fill of 0.35 m.

Table 1 Soil profile of BH 1
Full size table

3.2 Atterberg Limits Tests

The Atterberg limits tests were performed according to Australian Standard AS1289.3.1.2 (2009a) and AS1289.3.2.1 (2009b). Figure 4 shows the testing results for soil from BH 1. The soil is categorized as intermediate-plasticity clay (CI) between 0.5 m and 2.0 m, becoming high-plasticity at 3.0 m depth. Figure 4b reveals a slight variation in plastic limits from 15 to 16%, while liquid limits ranged between 26 and 37%. The linear shrinkage of soil ranged between 10.4% at 0.5 m and 14.6% at 3.0 m. The testing results suggest that the soil is low to moderate expansive (Austroads 2012).

Fig. 4
figure 4

Properties of soil from BH 1 (a) plasticity chart showing results of Atterberg limits (b) variation of plastic limit, liquid limit and linear shrinkage with depth

Full size image

3.3 Total Soil Suction and Water Content Profile

The total soil suction and water content profiles of the two BHs at different distances from the tree are shown in Fig. 5. Soil water content was determined following AS1289.2.1.1 (1992), while soil suction was measured using the Dewpoint Potentiometer WP4 based on the chilled-mirror dewpoint technique. Compared to the soil farther away from the tree (BH 1, drilled in February), the suction of the soil close to the dripline (i.e. BH 2, drilled in October) was significantly higher. Noticeable tree-induced soil desiccation from the ground surface to 2.5 m was observed from BH 2, with soil suction varied from 830 to 1550 kPa, which is, on average, 9% higher than soil suction over the same depths for BH 1. Soil water content profiles clearly show that overall, the soil at a distance away from the tree is wetter than the soil near the dripline, with considerably higher water content at 3.25 m. It is noticed that soil suction remains constant at the value of 610 kPa below 3.0 m for both BHs, and this is regarded as the deep equilibrium suction ueq for the site. The higher water content at 3.0 m for BH 1 was not reflected by the soil suction measurement for the same depth.

Fig. 5
figure 5

Soil test results for BH 1 and BH 2 in 2017 (a) suction profiles (b) water content profiles

Full size image

Comparing soil suction and water content measurement results between the ground surface and 2.0 m depth for BH 1 and BH 2, it is estimated that, on average, a change in water content of 1.9% corresponds to a suction change of approximately 100 kPa. Tree-induced soil drying between 1.0 m and 2.0 m is evident for samples collected from BH 2 in October, resulting in a constant suction value of approximately 1550 kPa over these depths, which could be taken as the wilting point suction uwp for the site. The maximum drying depth Ht of 3.0 m and ∆ubase of 940 kPa are inferred from Fig. 5a.

3.4 Ground Movement Estimation

The free ground movements ys as a result of local climate condition for the study site is determined using Eq. 1. Table 2 presents the detailed calculation for soil movements for each layer within the depth of Hs. The Ipt values were inferred from the shrink-swell index—plasticity index relationship developed by Cameron (2017). The ys of 16.3 mm is determined and the site is classified as Class S (slightly reactive).

Table 2 The ys determination for the study site
Full size table

The presence of the tree would create additional suction to soils as a consequence of tree root drying effects, which in turn result in extra soil movements yt based on ys. The yt of 22.7 mm was estimated using Eq. 2, assuming a maximum tree effect (e.g. Dt: HT < 0.5). The calculation details are presented in Table 3. The ∆ubase of 0.40 pF (940 kPa) and Ht of 3.0 m inferred from Fig. 5a were adopted in the calculation. Figure 6 compares the soil movement at various depths under the impact of a no-tree and a single tree case.

Table 3 The yt determination for the study site
Full size table
Fig. 6
figure 6

Comparison of ground surface movement with and without the tree’s influence. Note: Ground movement induced by the tree is determined by the sum of ys and yt for each soil depth considered. For example, surface soil movement due to the tree = 16.3 + 22.7 = 39 mm

Full size image

4 Field Monitoring Results

4.1 Soil Movement

The level survey was conducted on the steel pins installed on the north-east and south-west sides of the tree every three weeks from Dec 2017 to May 2021. The ground level was measured in relation to the BM level. Relative soil movements were determined based on the initial measurement taken in Dec 2017.

Figure 7 presents the level survey results for 16 pins on the south-west side of the tree over 42 months. Generally speaking, all surface soils have exhibited a similar variation trend, although the amount of movements varied slightly at different distances from the tree. The soil at a distance of 6.6 m from the tree (i.e. pin (9), Dt: HT = 0.5) had suffered the greatest shrinkage settlement of 13 mm compared to movements experienced by other pins. A noticeable heave was observed for all surface soil when the level survey was conducted in Feb 2018, with the most significant upward movement of 12.0 mm for pin (9). A marked movement, on average, from 3 mm to -6 mm was observed for all pins from Jul 2019 to Sep 2019. The Pin (1) located 8 m away from the tree (Dt: HT = 0.55) experienced the maximum soil surface movement of 16 mm; this value is very close to the calculated ys of 16.3 mm. Rainfall and mean daily temperature data were plotted against soil movement reading to see if there were any correlations, but no direct correlation was found. This could be attributed to the low permeability rate of clay soils, which takes time for rainwater to penetrate deeper soil layers after a rainfall event, resulting in a delayed increase in soil water content and subsequent soil expansion at these depths. On the other hand, if large cracks occur on the surface during hotter months, rainfall can readily penetrate deeper soil layers.

Fig. 7
figure 7

Variation in soil movements on the south-west side of the tree over 42 months

Full size image

Variation in movements of 12 pins installed on the north-east side of the tree was shown in Fig. 8. Soil movements exhibited similar variation trends as those located on the south-west side of the tree. Notably, Pin (21) experienced the largest settlement of 12 mm (Dt: HT = 0.7) when the level survey was conducted in Mar 2018. It is worth mentioning that considerable soil settlement may have happened far before the study period since the wilting point suction uwp (Fig. 5a) has already been established for the site.

Fig. 8
figure 8

Variation in soil movements on the north-east side of the tree over 42 months

Full size image

4.2 Tree Water Use

The Sap Flow Meter (SFM1) was installed on the north side of the tree at breast height to investigate the long-term water use by the C. maculata, as it provides a reliable, accurate and wide range of sap flow measurement in various field site environments (Burgess et al. 2001; Sun et al. 2022a, b). The SFM1 has a measurement range of −100 cm/hr–100 cm/hr, based on the user manual. The seasonal variations in sap flow rate for the C. maculata in 2019 are depicted in Fig. 9. The sap flow measurement was based on the assumption that tree cross section is symmetrical. Generally, the sap flow exhibited a bell-shaped pattern. The sap flow rate peaked in the early afternoon and then progressively declined until it reached around zero at midnight. Figure 9 reveals that the highest daily peak sap flow rate of 24 L/h occurred in mid-autumn, followed by a gradual decrease and reached the lowest rate of 5 L/h in winter and thereafter rose again in spring and summer.

Fig. 9
figure 9

Seasonal variations in sap flow rate for the C. maculata in 2019

Full size image

The monthly and cumulated water use by the tree in 2019 is presented in Fig. 10. This tree consumed 53 kL of water annually, with the highest water demand of 5.9 kL in December and the lowest monthly water use of 2.7 kL in June. The mean monthly water use is 4.4 kL. The tree used a maximum of 229 L of water in a day in summer and only required a minimum of 11 L of water to survive on a winter day.

Fig. 10
figure 10

Monthly and cumulative sap flow volume for the C. maculata in 2019

Full size image

5 Parametric Study

Parametric studies were carried out to examine the influence of various parameters on residential footing design and the corresponding construction cost. Footing size and reinforcement requirements were determined using commercial finite element software, CORD© (Code Orientated Raft Design), which is widely used in Australia for the design of residential footings and is recognized and recommended by the Australian Standard (CORD 2012). Footing details can vary when footings are designed with parameters of different values. This study compares the differences in footing size obtained using parameter values provided by AS2870 (2011) and that obtained from field site measurement. Many foundation failure cases arising in the past two decades have been the result of trees too close to dwellings (Li and Guo 2017). The effect of various Dt: HT ratios on footing size determination and construction cost was assessed.

A single-story, articulated masonry veneer house near the experimental site, constructed in 1995, was selected for the parametric study. Figure 11 shows the layout of the stiffened raft footing. In this study, the key parameters (e.g. Hs and ys) for designing a stiffened raft footing were inputted in CORD to check whether the selected footing size has met the design criteria (i.e. adequate footing stiffness, K; flexural strength, M and sufficient section ductility).

Fig. 11
figure 11

The stiffened raft footing used in this study (a) footing layout (b) cross-section A-A (all dimensions are in millimeters (mm) unless otherwise noted)

Full size image

5.1 Footing Design for Different Tree Scenarios

5.1.1 No Tree

To determine the footing size without the presence of trees, two primary parameters ∆us of 1.2 pF and Hs of 1.8 m recommended in AS2870 (2011) were adopted in the calculations using the CORD program. The ys of 16.3 mm (refer to Table 2) was used, assuming the footing was constructed on the study site.

The geometry of the footing layout (Fig. 11a) was divided into two overlapping rectangles, consisting of 3 sub-beams in the long direction and 4 sub-beams in the short direction. The internal and external beams (300 mm deep by 300 mm wide) reinforced with SL72 slab mesh (i.e., having a diameter of 7 mm and spaced at 200 mm centers in two directions) and 2-N12 bottom steel bar (12 mm in diameter with a yield strength of 500 MPa) were attempted. Based on the design rectangles and steel bar details, the design properties for the footing system were generated by CORD and were compared with the required values. Table 4 shows that the footing size and steel bar adopted have met the design criteria. The design summary of the stiffened raft footing is presented in Table 5. The most demanding design requirement is section ductility in edge heave.

Table 4 Design properties for a stiffened raft footing using parameter values provided by AS2870 (2011) for no tree scenario
Full size table
Table 5 Design information of a stiffened raft footing using parameter values provided by AS2870 (2011) for no tree scenario
Full size table

5.1.2 Single Tree

The parameter values of ∆us of 1.2 pF, ∆ubase of 0.33 pF, Hs of 1.8 m and Ht of 2.7 m given by AS2870 (2011) were used to determine the footing size and reinforcements requirements using CORD program, assuming the nearest corner of the footing was constructed at a distance of 0.5 HT from the tree at the study site. These are the essential parameters in establishing soil suction profiles needed for yt calculation and the subsequent footing design. The yt of 16.2 mm was estimated using Eq. 2.

The internal and external beams (350 mm deep by 300 mm wide) reinforced with SL72 slab mesh and 5-N12 rebar (two at the top and three at the bottom) were adopted. The design properties of the footing system in Table 6 confirm that the size of the footing and steel bar attempted have met the design criteria. The section ductility requirements are more stringent for tree design. Center heave becomes more critical for a growing tree near the footing and the structural requirements (flexural strength and moment of inertia) are more onerous.

Table 6 Design properties for a stiffened raft footing using parameter values provided by AS2870 (2011) for a single tree scenario
Full size table

The design summary of the stiffened raft footing is presented in Table 7. Compared to the footing construction cost for a no-tree scenario, building a stiffened raft footing close to a single tree would incur an additional steel reinforcement cost of $1095 and a concrete cost of $285 and thus a total of $1380. The cost was estimated based on the unit price provided by Scott Metals (2021) and Hanson Australia (2021). Design information of a stiffened raft footing using parameter values obtained from field site measurement is also presented in Table 7. Constructing such a footing near the tree would cost an extra $2030 compared with the footing built without the tree. It is worth noting that yt could be underestimated by 29% if adopting design parameter values recommended by the Standard, resulting in a smaller footing size and fewer steel bars and perhaps being insufficient to cope with the impact of tree root drying.

Table 7 Comparison of design information of a stiffened raft footing using parameter values provided by AS2870 (2011) with site measurement values for a single tree scenario
Full size table

5.1.3 A Group of Trees

The yt of 26.3 mm was calculated by assuming the nearest corner of the footing is located at a distance of 0.5 HT from a group of trees at the study site. The parameter values of ∆us of 1.2 pF, ∆ubase of 0.4 pF, and Ht of 3.3 m given by the Standard were inputted into CORD to carry out the design. The footing size and reinforcement details attempted have passed the design criteria, as shown in Table 8. The design summary of the footing in Table 9 reveals that compared to the no tree scenario, building a stiffened raft footing close to a group of trees would lead to a 150 mm increase in the footing depth, an extra 2-N16 top bars and an upgrade of bottom bars from N12 to N16. This results in an additional cost of $2710.

Table 8 Design properties for a stiffened raft footing using parameter values provided by AS2870 (2011) for a group of trees
Full size table
Table 9 Design information of a stiffened raft footing using parameter values provided by AS2870 (2011) for a group of trees
Full size table

5.2 The Influence of D t: HT on Footing Design and Construction Cost

Tree growing close to buildings can lead to foundation failure and wall crack due to substantial soil movements as a result of tree root drying. This parametric study assesses the influence of different Dt: HT ratios ranging from 0.1 to 1.0 on yt, footing size, steel bar requirements and construction cost. Design values ∆us of 1.2 pF, Hs of 1.8 m and those obtained from the site measurement (e.g. Ht = 3.0 m and ∆ubase = 0.4 pF) were used to calculate yt, which was then imported into CORD to determine the footing details. Additional construction cost was calculated and compared for different footing specifications. Table 10 presents footing design details and the consequent additional construction cost estimated based on various Dt: HT ratios. All footing calculations have been checked using CORD and have achieved the design criteria. The additional cost is relative to the cost for a footing size determined using a Dt: HT ratio of 1. Table 10 reveals that the influence of a tree on footing determination can be neglected (i.e. yt = 0 mm) if the tree is located at a distance of HT to a building (e.g. Dt: HT is 1).

Table 10 Comparison of footing details and construction cost calculated based on various Dt: HT ratios
Full size table

Figure 12 depicts the relationship between Dt: HT ratio, yt and construction cost. The maximum yt is calculated when the distance of the tree to the house is less than half the tree height (i.e. 0.1–0.5 HT). The yt decreases gradually as the distance is released (e.g. Dt: HT > 0.5), resulting in a drop in the construction cost. It is evident that the footing construction cost is the highest when the yt is the largest. The cost can be cut by about 32% if the footing is constructed at a distance of 0.6 HT from the tree compared to the cost of 0.1–0.5 HT. Tree-induced additional ground movement is 0 mm when Dt: HT is 1, and thus no cost would be incurred.

Fig. 12
figure 12

Relationship between Dt: HT, yt and construction cost

Full size image

6 Conclusions

In this study, the ground movements at various locations from an Australian native, C. maculata, located in a clay site in Melbourne, Australia, were closely monitored by the authors over 42 months. The level survey results reveal that the soil movements exhibited similar variation trends on the south-west and north-east side of the tree, although the amount of movements varied slightly at different distances from the tree. The survey steel pin (9) at a distance of 0.5 HT away from the tree had experienced a significant shrinkage settlement of 13 mm compared to movements suffered by other pins. There was a noticeable movement from 3 to −6 mm for all pins from Jul 2019 to Sep 2019. It should be noted that substantial soil settlement may have occurred well before the monitoring period as the wilting point suction uwp has already developed for the site.

The total soil suction and water content profiles established using samples from two BHs located at different distances from the tree show a noticeable tree-induce soil drying between 1.0 m and 2.0 m depth close to the dripline (e.g. BH 2), resulting in a constant suction value of 1550 kPa over these depths, which could be regarded as the wilting point suction uwp. Suction remains constant at 610 kPa below 3.0 m depth for both BHs, and this can be taken as the deep equilibrium suction ueq for the site. The developed suction change profile reveals that the effect of tree root drying has extended to a depth of 3 m.

The water use of the C. maculata was closely monitored using sap flow meters, and the monthly sap flow data in 2019 show that the tree had the highest transpiration of 5.9 kL in December and the lowest water demand of 2.7 kL in June. The tree only needed a minimum of 11 L of water to survive on a winter day, compared to the maximum daily water consumption of 229 L in the summer.

A parametric study was carried out to examine the influence of various parameters on footing design for the effect of trees and the consequent construction cost. It was found that building a footing at a distance of 0.6 HT from the tree could result in a 32% cost savings for homeowners compared to the cost for a footing constructed at a distance less than or equal to 0.5 HT. The impacts of various parameters given by the Australian Standard on the residential footing design and construction cost for different tree scenarios were also evaluated. The results show that building a stiffened raft footing close to a single tree and a group of trees would incur an additional cost of $1380 and $2710, respectively, compared to the cost for a no tree scenario. It was found that yt could be underestimated by 29% for a single tree scenario if using design parameter values provided by the Standard, resulting in a shallow footing that might not be able to cope with the effect of tree root desiccation. The influence of various Dt: HT ratio on footing size and construction cost was also assessed for a single tree scenario and found that the cost can be cut by 32% if the footing is constructed at a distance of 0.6 HT from the tree when compared to the cost for 0.1–0.5 HT. Homeowners could avoid extra construction costs for a footing built at a distance greater or equal to HT from the tree.