Interfaces in dynamic brittle fracture of PMMA: a peridynamic analysis

Abstract

Recent experiments in bonded PMMA layers have shown dramatic changes in dynamic crack growth characteristics depending on the interface location and its toughness. We present a peridynamic (PD) analysis of the problem and identify three necessary elements in a model aimed at reproducing the observed dynamic fracture behavior at an interface in PMMA: (1) softening near the crack tip to account for changes in PMMA properties due to heat-generation induced by the high strain rates reached around the crack tip in dynamic fracture, (2) independence of extension (mode I) and shear (mode II) modes of fracture, and (3) a two-parameter bond-failure model, that can match both strength and fracture toughness for any horizon size. The PD model with these elements captures the experimentally observed dynamic fracture characteristics in bi-layer PMMA: the presence/absence of crack branching at the interface, depending on the interface location; cracks running along the interface for a while before punching through the second PMMA layer; slight crack path oscillations as the cracks approach the free surface. The computed crack speed profiles are close to those measured experimentally. The simulations help explain the observed behavior of dynamic crack growth through an interface. The model shows an enlargement of the fracture process zone when the cracks running along the interface penetrate into the second PMMA layer, as observed experimentally. This is where nonlocality of the PD model becomes relevant and critical.

Appendix

To demonstrate the criticality of each of the model components discussed in Sect. 4, we show from PD models that lack as least one of the essential components. We also show results from a PD model in which interface bonds are also softened, to mimic the potential sensitivity of the glue to rapidly propagating cracks.

1.1 Results from models missing at least one critical component

The PD model introduced in Section 4, three elements were called “critical”: (1) the HAZ that softens bonds around the crack tip to account for changes in PMMA mechanical properties due to heat generated by the rapidly propagating crack; (2) independent modes of fracture (mode I independent from mode II, achieved here by using a special case of a state-based model); and (3) a bi-linear model for bond-failure (bond-softening before final failure), capable to match both a given fracture toughness and the material strength, with any horizon size.

The influence of the HAZ has been studied in our previous study (Mehrmashhadi et al. 2019b). Without HAZ, the simulated crack propagation velocity in PMMA is around twice as fast as the experimentally measured values. In Fig. 21, we compare the crack propagation velocity in the case with the interface at 7mm.

Fig. 21

Comparisons of crack propagation speed (PD models with and without HAZ) in the bi-layered PMMA with the interface location at 7 mm. Experimental results from Sundaram and Tippur (2016a)

Having independent modes of fracture (mode I independent from mode II) is also critical to accurately capturing the mode-II dominated fracture along the interface. In Fig. 22, we show the results from bond-based models in which the mode II fracture is not independent from mode I. We observe that for the cases with the interface located at 17 and 28 $\mathrm{mm}$, the cracks do not branch at the interface, and do not run along the interface.

Fig. 22

Damage maps at 240 $\mathrm{\mu s}$ (from the moment the loading is applied) obtained with the PD bond-based model (mode II not independent from mode I) for the bi-layered PMMA with interface location at: a 7 mm, b 17 mm, c 28 mm, and d 42 mm

A bond-failure model that uses a sudden drop of bond force from its highest value to zero (a one-parameter bond-failure model) can only match, for a given horizon size, either the fracture toughness or the material strength. Using this model with a critical bond strain matched to the fracture toughness, for example, will match a material’s strength for a particular size of the PD horizon. That size, however, may turn out to be extremely small and thus not usable for practical computations. A two-parameter bond-failure model, however, can match both the fracture toughness and the material strength, for any horizon size [see (Niazi et al. 2020) for details]. Matching material strength is critical in obtaining crack initiation at the correct stress levels in samples in which there are no pre-cracks. This is exactly our case in which we have crack initiation at the interface (before the main crack arrives there) and crack initiation into the second PMMA layer. Simulation results from a model that uses a one-parameter bond-damage model instead of the bi-linear model used in the main text of the paper are shown in Fig. 23. While branching appears to happen at the interface for the 17, 28, and 42 mm, there is very little propagation along the interface.

Fig. 23

Damage maps at 240 $\mathrm{\mu s}$ (from the moment the loading is applied) from the PD model with a one-parameter bond-damage model for bi-layered PMMA with the interface location at: a 7 mm, b 17 mm, c 28 mm, and d 42 mm

1.2 Results from model with heat-induced softening of interface bonds

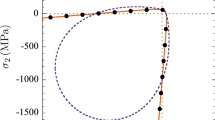
While we do not have available data on the temperature variation of material properties for the glue material used in the PMMA bi-layered structure, it may be reasonable to assume a similar type of behavior as the HAZ model we used for PMMA. We therefore assume that interface bonds are affected by heat. In the model used here we do not include the independent modes of fracture (we use the bond-based model), nor the bi-linear bond-failure model. We hypothesize that the glue is more sensitive to the high temperatures caused by the rapid crack propagation, compared with PMMA. We use the bilinear model (pink dash line) shown in the figure below. The micromodulus of interface bonds decreases to 0.01 ${c}_{glue}$ when the bond strain is larger than 0.1 ${s}_{0}$ (Fig. 24).

Fig. 24

Heat-affected model for interface bonds

The constitutive model for interface bonds in the HAZ is:

$${\varvec{f}}\left({\varvec{\eta}},{\varvec{\xi}}\right)=\left\{\begin{array}{c}\frac{{\varvec{\eta}}+{\varvec{\xi}}}{\Vert {\varvec{\eta}}+{\varvec{\xi}}\Vert }c\left({\varvec{\xi}}\right)\left[0.01s+0.099{s}_{0}\right], \; \text{if}\; s>0.1{s}_{0} \; \text{and}\; {\lambda }_{HAZ}=1 \\ \frac{{\varvec{\eta}}+{\varvec{\xi}}}{\Vert {\varvec{\eta}}+{\varvec{\xi}}\Vert }c\left({\varvec{\xi}}\right)s, \; \text{otherwise}\end{array}\right.$$

(39)

Similar to Eq. (37), to maintain the fracture energy ${G}_{0}$ the same, the following condition needs to be satisfied (areas under linear and bilinear functions need to match) for the interfacial bonds:

$$\frac{1}{2}{{s}_{0}}^{2}=\frac{1}{2}{\left(0.1{s}_{0}\right)}^{2}+\left(0.1{s}_{0}\right)\left({s}_{glue-bi-0}-0.1{s}_{0}\right)+\frac{1}{2}\left(0.01\right)$$

(40)

The critical strain ${s}_{glue-bi-0}$ for the bilinear function of interface bonds is 4.23 ${s}_{0}$.

With this model, the damage maps for PMMA samples with weak/strong interface and samples with different interface locations are shown below. The histories of the crack tip propagation speeds are compared with experiments as well. In Figs. 25 and 26, the crack path and crack velocity of PMMA samples with weak/strong interface match well with the experiments.

Fig. 25

Damage maps from the bond-based PD model with heat-induced softening of interface bonds for bi-layered PMMA with: a weak interface, and b strong interface

Fig. 26

Comparisons between experimental results (from Sundaram and Tippur 2016b) and results obtained with the bond-based PD model with heat-induced softening of interface bonds for crack propagation speed in the bi-layered PMMA with: a strong interface, and b weak interface

However, since in the regular bond-based model (with one-parameter bond-failure model), the mode II fracture is not independent from mode I fracture, and the material strength will differ depending on the horizon size, mode II-dominated fracture and crack initiation along the interface are not going to be accurately captured. Indeed, as seen from Fig. 27, the crack lengths along the interface obtained by these simulations, especially when d = 42 mm, are significantly smaller compared with the experimental results (Sundaram and Tippur 2016a). Also, when d = 7 mm, the crack branches inside the second layer of PMMA, which is not observed in experiments (Sundaram and Tippur 2016a). Since the HAZ in PMMA is considered here, crack propagation speeds, shown in Figs. 26 and 28 are in good agreement with experiments.

Fig. 27

Damage maps from the bond-based PD model with heat-induced softening of interface bonds for bi-layered PMMA with the interface location at: a 7 mm, b 17 mm, and c 42 mm

Fig. 28

Comparisons between experimental results (from Sundaram and Tippur 2016a) and results obtained with the bond-based PD model with heat-induced softening of interface bonds crack propagation speed in the bi-layered PMMA with the interface location at: a 7 mm, b 17 mm, and c 42 mm